【数理溢れ話】【Token】複素円筒座標系(Complex Cylindrical Coordinate System)からリーマン球面(Riemann Sphere)へ

以下の投稿において「符号なし数直線(Unsigned Rational Set)」kの概念まで定義しました。
【数理溢れ話】【Token】実数概念の代用品としての「連続有理数集合」

今回はこの概念の幾何学的拡張を試みたいと思います。

「符号付数直線(Signed Rational Set)」への拡張

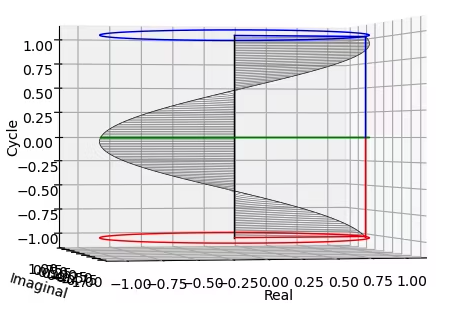
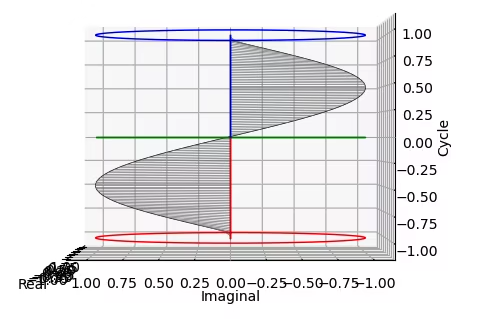
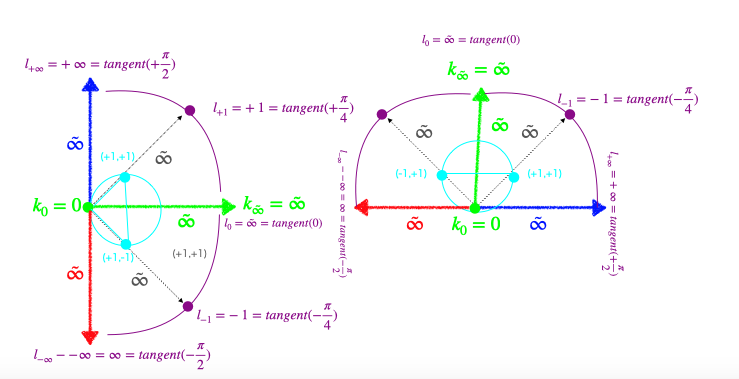
まずは上掲の符号なし有理数集合kに三角関数tangentを導入する。すると直交写像(Orthogonal Mapping)として符号付き有理数集合lが得られる。

Wikipedia「写像」

中心０よりtangent($±\frac{π}{2}$)の方角に伸ばされた垂線上ではそれぞれk上の元とl上の各符号ごとの元の絶対値(Absolute Value)が全単射対応するのを利用し直交座標(l,m)上の(+1,+1)(-1,-1)を任意に定め、これを基準とする平方眼と対角線を得る。なおこの段階においては、xy直交座標系のx,yそれぞれにどうkとlを射影するかはまだ不定のままである。

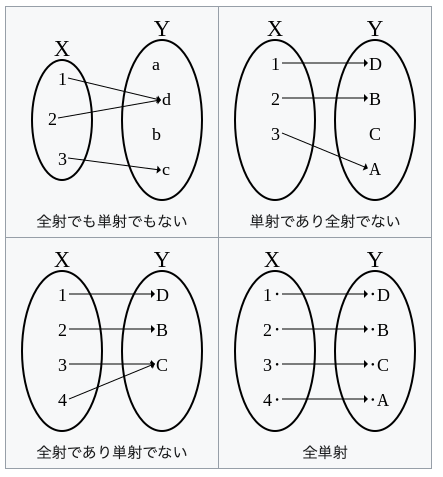
この方眼に座標(0,0)を頂点として座標(+1,+1)と座標(+1,-1)を通る円錐座標系(Conical Coordinate System)と、座標(1,0)を中心とする半径1の球面座標系(Spherical Coordinate System)を置きたいが、その前にこの座標系全体のイメージをもっときっちり構成し直す必要が生じる。

「複素円筒座標系(Complex Cylindrical Coordinate System)」への拡張

ここで考え方を変えてみよう。①虚数(Imaginal Set)の対語としての実数直線(Real Set)は、その値を変えない単位元「1」を半径とする 「複素円筒座標系(Complex Cylindrical Coordinate System)」へと容易に拡張出来る。さらに(とりあえず等差数列として構成される)実数直線と直交する半径1の水平円は容易にこれを$α^0$と置く等比数列に拡張可能だが、この段階では角度が不明な為複素座標系しか構成出来ない。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*2,121,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,121,endpoint = True)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(-0,61)
uz2=num.repeat(1,61)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    #円柱描画
    ax.plot(s1.real,s1.imag,z0,color="black",lw=0.5)
    #スポーク描画
    for nm in range(len(s1)):
        ax.plot([0,s1[nm].real],[0,s1[nm].imag],z0[nm],color="gray",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,-1],[0,0],[0,0],color="green",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転
    ax.view_init(elev=10, azim=Time_code[n])

Time_code0=num.arange(0,360,6) 
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output505.gif", writer="pillow")

実はまだ数理を整えてないだけで、この段階において既に側面からの観測で「正面図(x=-∞→+∞)」にCosine(θ)波を捉えた時、「側面図(y=-∞→+∞)」に(周期が$\frac{1}{2}ズレた$)Sin(sin(θ)波が現れている。だから円関数Cos(θ)+Sin(θ)は自明の場合の様なものだが、詳しい論証は後回しにしよう。

• 上掲図においてx軸上に現れるCos(θ)並
  

• 上掲図においてy軸上に現れるSin(θ)波
  

ここでしっかり把握しておいて欲しいのは、①球面座標系においては水平面上の直線的推移が半分の距離の往復運動として観察される。②全体として複素円筒座標系を構成する訳だから、上掲のTangent遷移図はその回転断面として規定される、③とりあえずこの複素円筒座標系では実数の等差数列を垂直軸、虚数の等比数列を水平軸とするの3点。

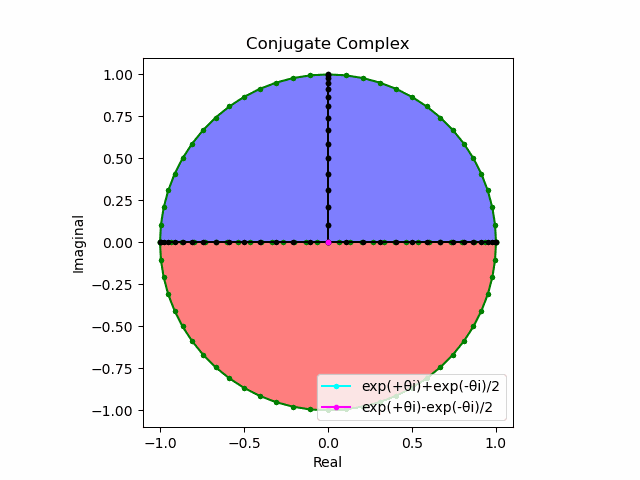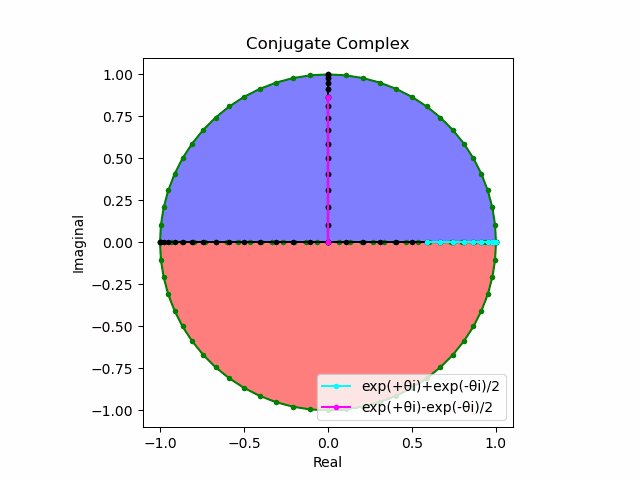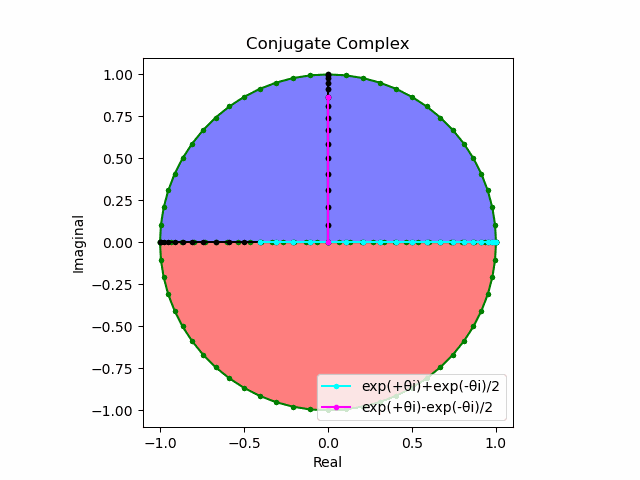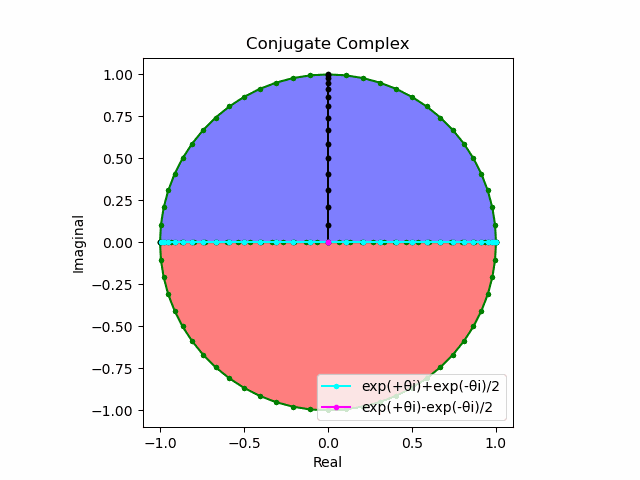
import math as m
import cmath as c
import numpy as num
from matplotlib import pyplot as plt
import matplotlib.animation as animation

#単位円データ作成
z=num.linspace(1,-1,31,endpoint = True)*(1+0j)
zp=z*(0-1j)
p0=[]
for nm in range(len(zp)):
    p0.append(c.exp(zp[nm]*m.pi/2)*(0+1j))
p1=num.array(p0)
#共役複素数列(-)
m1=-p1[::-1]
lx=(p1+m1)/2
ly=(p1-m1)/2

#グラフ表示準備
plt.style.use('default')
fig = plt.figure()

#関数定義
def Conjugate_Complex(n):
    plt.cla()
    plt.plot(z.real,z.imag,color="green", marker=".")
    plt.plot(p1.real,p1.imag,color="green", marker=".")
    plt.plot(m1.real,m1.imag,color="green", marker=".")
    plt.fill_between(p1.real,p1.imag,facecolor='blue',alpha=0.5)
    plt.fill_between(m1.real,m1.imag,facecolor='red',alpha=0.5)
    plt.plot(lx.real,lx.imag,color="black", marker=".")
    plt.plot(ly.real,ly.imag,color="black", marker=".")
    plt.ylim([-1.1,1.1])
    plt.xlim([-1.1,1.1])
    plt.title("Conjugate Complex")
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    ax = fig.add_subplot(111)
    ax.set_aspect('equal', adjustable='box')
    #exp(+θi)±exp(-θi)
    plt.plot(lx[0:n].real,lx[0:n].imag,color="cyan", marker=".", label="exp(+θi)+exp(-θi)/2")
    plt.plot([0,ly[n].real],[0,ly[n].imag],color="magenta", marker=".", label="exp(+θi)-exp(-θi)/2")
    ax.legend(loc='lower right')

ani = animation.FuncAnimation(fig, Conjugate_Complex, interval=50,frames=len(z))
ani.save("output93.gif", writer="pillow")

円錐座標系(Conical Coordinate System)と、球面座標系(Spherical Coordinate System)

上掲のTangent遷移図で得られた符号付き有理数直線lにそれと直交する符号付き有理数直線mを追加し。さらにこのmとnを一次関数y=xの定義域(始域)と値域(終域)に割り振ると新たに対角線集合nを得ます(対称式なのでxとyは可換)。
Wikipedia「定義域(始域)」
Wikipedia「値域(終域)」

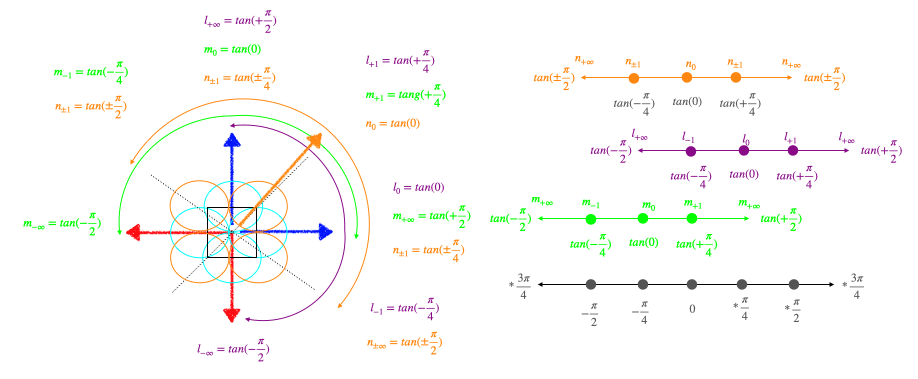
ここで興味深いのが対角線集合nの符号が不定である事。これは(球面の赤道に対応する)水平面からの観察結果では任意の座標に必ず北半球(+か-)と南半球(北半球が+の時-、-の時+)でピッタリ重なってしまう座標が存在するせいである(いわゆる複素共軛)。

Wikipedia「複素共軛(Complex Conjugate）」
まさしくこの図における(垂直方向に観察された方の)Sin(θ)波の振る舞いそのもの。

最終的には水平方向の向きなんて関係ない感じに。

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.sqrt(1-cutz**2)
cuty=num.repeat(0,61)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(0,61)
uz2=num.repeat(1,61)

#断面円
ucv0=num.linspace(-1,1,61,endpoint = True)
ucv=num.sqrt(1-ucv0**2)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    ucutz=num.full(61,cutz[n])
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for nm in range(len(uc)):
        ax.plot([0,uc[nm].real*ucv[n]],[0,uc[nm].imag*ucv[n]],[cutz[n],cutz[n]],color="black",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1.5)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,cutx[n]],[0,cuty[n]],[0,cutz[n]],color="purple",lw=1)
    ax.plot([0,cutx[n]],[0,cuty[n]],[cutz[n],cutz[n]],color="purple",lw=1)
    ax.plot([0,cuty[n]],[0,cutx[n]],[0,cutz[n]],color="blue",lw=1)
    ax.plot([0,cuty[n]],[0,-1*cutx[n]],[0,cutz[n]],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="purple",lw=1)
    ax.plot([0,0],[0,1],[0,0],color="blue",lw=1)
    ax.plot([0,0],[0,-1],[0,0],color="red",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #断面線描画
    ax.plot(cutx,cuty,cutz,color="purple",lw=1)
    ax.plot(cuty,cutx,cutz,color="blue",lw=1)
    ax.plot(cuty,-1*cutx,cutz,color="red",lw=1)
    #断面円描画
    ax.plot(uc.real*ucv[n],uc.imag*ucv[n],ucutz,color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示に)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=num.arange(0,360,6)  
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output521.gif", writer="pillow")

要するに三角関数とは「任意の直線がその絶対値を変えないまま回転する様子の水平写像ないしは垂直写像」の事で、全体として球面座標系(Spherical Coordinate System)を構築。一方、円錐座標系(Conical Coordinate System)においては、高さによって水平断面円の半径そのものが変化していく。

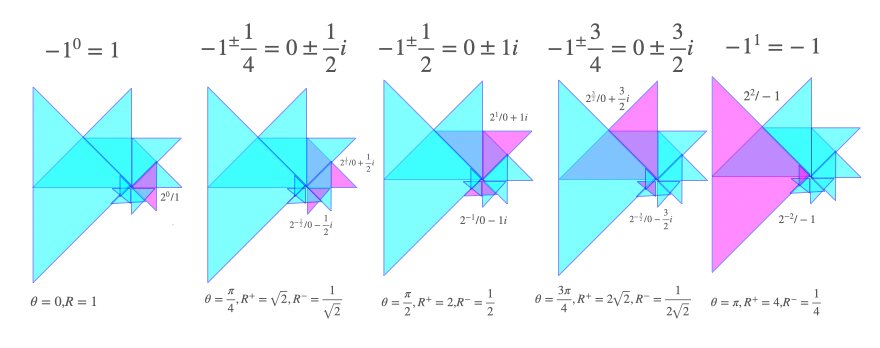
ちなみに垂直軸に±の符号をどう与えるかはなかなか難しい問題で、例えば有名な「ハミルトンの四元数(Hamilton's quaternion))」ではc$i^2=j^2=k^2=ijk=-1$と規約したが(四元数の定義バリエーションはこれだけではない)、それにまつわる操作複雑化を余儀なくされている。
【数理溢れ話】【Token】「ハミルトンの四元数」

円錐曲線(Conic Curve)とLp空間(Lp Space)

もうすでに十分ややこしいのに、ここに「円錐座標系における水平断面の回転」を扱う円錐曲線(Conic Curve)概念が登場。
Wikipedia「円錐曲線(Conic Curve)」

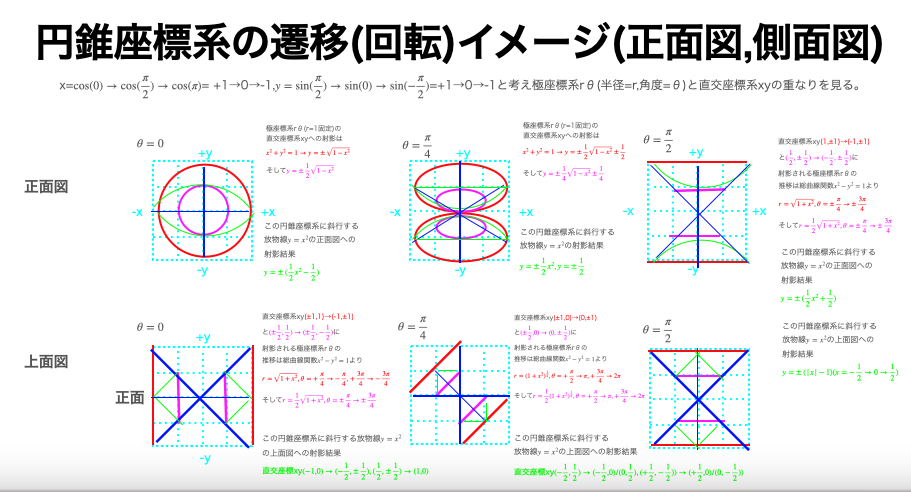
そしてさらには以下の式が円概念と放物線概念と双曲線概念を統合する。

r=\frac{1}{1±ε \cos(θ)}

• ε=0の時,r=1(-πθ)→1(0θ)→1(πθ)、つまり円(Circle)
• 0<ε<1の範囲の時,楕円(Ellipse)
• ε=1の時,r=∞(-πθ)→$±\frac{1}{2}$(0θ)→∞(πθ)、つまり放物線(Parebora)
• ε<1の時、双曲線(Hyperbora)
• 特にε=$\frac{π}{2}$の時、第一象限上の頂点と第三象限上の頂点、第二象限上の頂点と第四象限上の頂点を結ぶ直線がx軸上の±1で交差する。

ここで式$r=\frac{1}{1＋ε \cos(θ)}$と式$r=\frac{1}{1-ε \cos(θ)}$は複素共役(Complex Conjugate)と似た関係にあり、ε=0あるいはε=∞の場合のみその値が重なる。

import numpy as np
import cmath as c
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#figure()でグラフを表示する領域をつくり，figというオブジェクトにする．
plt.style.use('default')
fig = plt.figure()
ax = fig.add_subplot(111,aspect='equal')

#1周分の角度
θ=np.linspace(0,np.pi*2,61,endpoint = True)

#ε(離心率)
ε=np.linspace(0,5,51,endpoint = True)

#円、放物線、双曲線の計算
def eccentric(x):
    return(1/(1+x*np.cos(θ)))

def eccentricity(x):
    c0=[]
    for nm in range(len(θ)):
        c0.append(c.rect(eccentric(x)[nm],θ[nm]))
    return(np.array(c0))

C1=eccentricity(0)
C2=eccentricity(1)
C3=eccentricity(np.pi/2)

#描画関数
def Eccentricity01(n): 
    plt.cla()
    fp0=[]
    for nm in range(len(θ)):
        fp0.append(c.rect(1/(1+ε[n]*np.cos(θ[nm])),θ[nm]))
    xyp=np.array(fp0)
    fm0=[]
    for nm in range(len(θ)):
        fm0.append(c.rect(1/(1-ε[n]*np.cos(θ[nm])),θ[nm]))
    xym=np.array(fm0)
    #描画
    plt.plot(C1.real,C1.imag,color="salmon",lw=0.5,label="ε=0(Circle)")
    plt.plot(C2.real,C2.imag,color="green",lw=0.5,label="ε=1(Parabola)")
    plt.plot(-C2.real,C2.imag,color="green",lw=0.5)
    plt.plot(C3.real,C3.imag,color="olive",lw=0.5,label="ε=π/2(Hyperbola)")
    plt.plot(-C3.real,C3.imag,color="olive",lw=0.5)
    es="{:0<+7}".format(round(ε[n],3))
    ES="ε="+es
    plt.plot(xyp.real,xyp.imag,color="blue",marker="o",lw=1,label=ES)
    plt.plot(xym.real,xym.imag,color="red",marker="o",lw=1,label=ES)
    plt.axvline(0, 0, 1,color="black",lw=0.5)
    plt.axhline(0, 0, 1,color="black",lw=0.5)
    plt.xlim([-18,18])
    plt.ylim([-18,18])
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    plt.title("Eccentricity")
    ax.legend(loc='upper right')

#Eccentricity01(10)
#plt.show()

ani = animation.FuncAnimation(fig, Eccentricity01, interval=100,frames=len(ε))
ani.save("Ecc102.gif", writer="pillow")

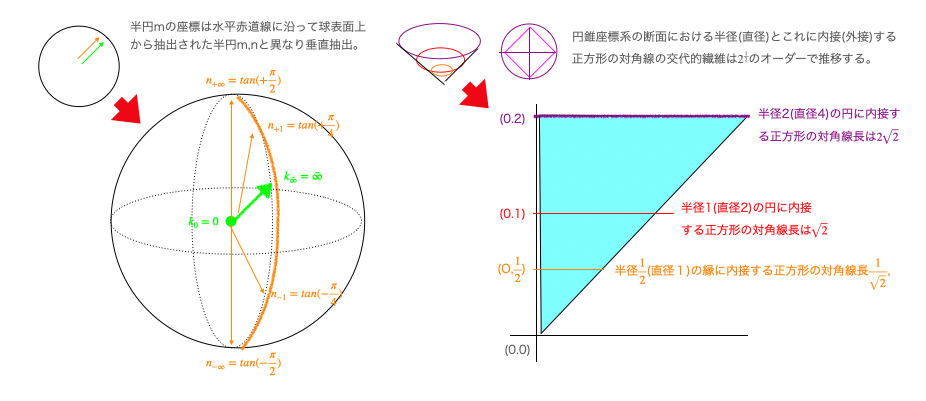
特に円錐座標系をイメージする上で大事だと感じたのは以下の対比。

• 式 $y=\sqrt{1-x^2}$は、直交座標上に半円(回転断面)を描く(半径は一定)。
• 式 $y=\sqrt{1+x^2}$は、極座標上に直線(角度範囲$+\frac{π}{4}$→-$\frac{π}{4}$)を描く(半径が$\sqrt{2}→1→\sqrt{2}$と連続的に推移)。

さらには「xy直交座標系(0,1)(1,0)の間をどう結ぶか」執拗に研究したLP空間論なんてのもあって人工知能分野などでも大いに役立てられている模様。
Wikipedia「LP空間」

||x||_p=\sqrt{|x_1|^p+|x_2|^p+…+|x_n|^p}^{\frac{1}{p}}

式形を見ても分かる様にユークリッド距離(絶対値)を求めるしきの拡張概念。

cx<-seq(0,1,length=61)
f0<-function(x,p){(1-(x^p))^(1/p)}
cy10<-f0(cx,1/10)
cy15<-f0(cx,1/1.782273)
cy20<-f0(cx,1)
cy30<-f0(cx,2)
cy40<-f0(cx,99)
plot(cx,cy10,type="l",asp=1,xlim=c(0,1),ylim=c(0,1),main="p-Norm",xlab="",ylab="",col=rgb(1,0,1))
par(new=T)
plot(cx,cy15,type="l",asp=1,xlim=c(0,1),ylim=c(0,1),main="p-Norm",xlab="",ylab="",col=rgb(1,1,0))
par(new=T)
plot(cx,cy20,type="l",asp=1,xlim=c(0,1),ylim=c(0,1),main="",xlab="",ylab="",col=rgb(0,1,0))
par(new=T)
plot(cx,cy30,type="l",asp=1,xlim=c(0,1),ylim=c(0,1),main="",xlab="",ylab="",col=rgb(1,0,0))
par(new=T)
plot(cx,cy40,type="l",asp=1,xlim=c(0,1),ylim=c(0,1),main="",xlab="",ylab="",col=rgb(0,0,1))
# 凡例を書き添える 。
legend("bottomleft", legend=c("p=0.1","p=1/1.78…","p=1","p=2","p=99"), lty =c(1,1,1,1,1),col=c(rgb(1,0,1),rgb(1,1,0),rgb(0,1,0),rgb(1,0,0),rgb(0,0,1)),cex=0.8) 

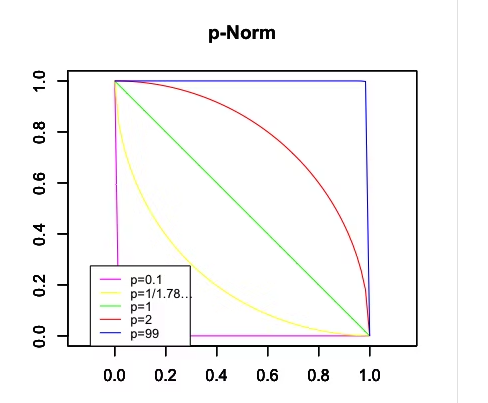
• ほとんど(0,1)→(0,0)→(1,0)と進む(距離2)のが$L_0$ノルム($\frac{1}{10}$でも結構小さい)
• 通常のユークリッド距離(距離$\sqrt{2}$)が$L_1$ノルム
• $\frac{1}{4}$円弧を描くのが(距離$\frac{π}{2}$)のが$L_2$ノルム
• ほとんど(0,1)→(1,1)→(1,0)と進む(距離2)のが$L_∞$ノルム(99でも結構大きい)

特に「L2空間の真逆の$\frac{1}{4}$円弧が軌跡として現れる(距離$\frac{π}{2}$)」pノウム=1/1.782273(=0.561081276)は垂直/水平座標系と対角線座標系、偶奇かんけいなどにも関わってくる重要な性質なので、引き続き注目していきたいところ…

「リーマン球面(Riemann Shere)」への拡張

正確には私は以下の内容を完全に理解出来てる訳ではないので「それっぽい何か」としか言い様がない。従って以下は「とりあえず私が理解したと信じている内容」という事になる。
Wikipedia「リーマン球面(Riemann Shere)

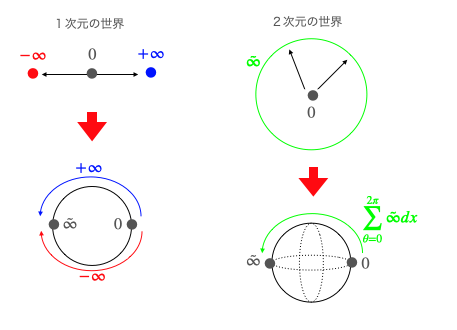
出発点はやはり冒頭に挙げた有理数直線。その片端である無限遠点には独特の不定性があり、符号付き無限直線の両端(2個)や観察原点0を囲む円弧(全方向=0→±π)という形でも現れるが指数写像/対数写像などの操作によって再び単一の点として観察される様になる。

• １次元の場合
  

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from functools import reduce
from itertools import accumulate
import matplotlib.animation as animation

def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=num.repeat(RIM/n,n)
    Tarm=num.concatenate([[(1+0j)], Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
c0=num.linspace(0,2*m.pi,61,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
plt.style.use('default')
fig = plt.figure(111)

#関数定義
def Eulerien_Identity(n):
    plt.cla()
    #ネイピア数算出
    ei01=num.array(list(Napier_culc(ABS,Time_Code[n])))
    EI0=[]
    for nm in range(len(ei01)):
        EI0.append(ei01[nm].conjugate())
    ei02=num.array(EI0)
    #円周描画
    plt.plot(s1.real,s1.imag,color="green", label="Circle")
    plt.plot(ei01.real,ei01.imag,color="blue", label="(1+1/n)^n")
    plt.plot(ei02.real,ei02.imag,color="red", label="(1-1/n)^n")
    plt.xlim([-m.pi,m.pi])
    plt.ylim([-m.pi,m.pi])
    plt.title("Eulerean Identity")
    plt.xlabel("Real")
    plt.ylabel("Imaginal")
    ax = fig.add_subplot()
    ax.set_aspect('equal', adjustable='box')
    #補助線描画
    plt.axvline(0, 0, 1,color="black")
    plt.axhline(0, 0, 1,color="black")
    plt.plot([-1,0],[0,0],color="red",lw=1)
    plt.plot([0,1],[0,0],color="blue",lw=1)
    ax.text(0, 0, "0",color="black",size=13)
    ax.text(1, 0, "1",color="blue",size=13)
    ax.text(-1, 0, "-1",color="red",size=13)
    ax.text(0, 1, "π",color="green",size=13)
    ax.text(0, -1, "-π",color="green",size=13)
    #凡例描画
    ax.legend(loc='lower right')

ABS=1
Time_Code=[1,2,4,8,16,32,64,128]

#Eulerien_Identity(0)
#plt.show()

ani = animation.FuncAnimation(fig, Eulerien_Identity, interval=100,frames=len(Time_Code))
ani.save("EI01.gif", writer="pillow")

• 2次元の場合
  
  
  

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.real,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="olivedrab",lw=0.5)
    ax.plot(uc.real,uc.imag,uz2,color="green",lw=1)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([0,np.pi*2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map100001.gif", writer="pillow")

それに加え「(-∞から+∞にかけて推移する)無限連続線を距離2に射影する」なる、プラネタリュームの半球型スクリーンを連想させるコンセプトに魅了された。

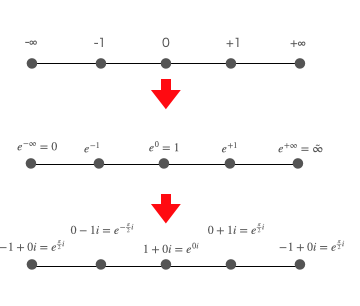
考え方としてはこういう感じ？

f(x) = \left\{
\begin{array}{ll}
e^x & (x < 0)\\
e^0=1 & (x = 0)\\
2-e^{-x} & (x > 0)
\end{array}
\right.

そしてtangent概念導入によって拡張された上掲座標系との関係はこんな感じ？

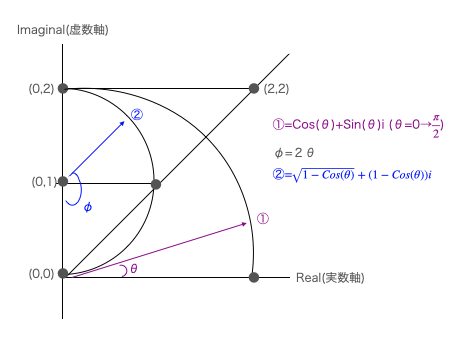
この考え方が正しい方向を向いているかどうか確かめる為にも、ますます複素関数輪についての知識を深めねばならない。何しろ現状は入門書すら満足に最後まで読み通せないレベルという…

この考え方の効用

実は別サイトで「私がこういう風に認識している」リーマン球面概念を主体認識(Subject recognition)の説明に使えないか試みています。例えば近世において期間会計と文書行政の概念導入を契機として欧州に誕生した「(国体の保全に充分な火力と機動力を有する常備軍を中央集権的官僚制による徴税で賄う)主権国家体制」。国家ごとに開始時点の規模がまちまちな上、以降の成長や衰退が倍率でしか測れないので「揃え方が見つかった次元の部分比較」しか出来ない辺りが「単位元1が不定で、上限♾️にも下限0にも到達する事なく往復を続ける」リーマン球面の特徴と重なりそうに感じたのです。
【とある本格派フェミニストの憂鬱3パス目】こんにちは、そしてさよならナチズム

とはいえその割に以下の定義を読んでも珍紛漢紛。複素関数論についての知識が徹底して足りてないせいですね。
Wikipedia「リーマン球面」
リーマン球面と無限遠点 | 高校数学の美しい物語
複素解析での無限遠点とは – リーマン球面への立体射影
リーマン球面 - 数学
リーマン球面と無限遠点｜複素数から実数への変換【複素解析】

こうした全体像を俯瞰して思い出したのがコンピューターGameのジャンルの一つであるTPS(Third Person Shooting)。

視界全体は、上掲の説明における「tangent的」な感じですが、そこに自分の姿が映り込んでる感じが「リーマン球面的」です。リーマン球面系の座標イメージ的には元来「足下あるいは尻側から空を見上げる」感じな訳ですが「空飛ぶスーパーマン」とかまさにそんな感じな訳で…時間が取れ次第随時pythonアニメーションで動作を確認していきたいと考えてますが、とりあえずその準備稿として投稿。