1. はじめに
自分のこれまでの経験を振り返って考えて見ると、なにごとも、勉強をする上で急に難しくなり乗り越えないと理解を次に進めることができない急所のようなものがあると思っています。そして、数学の勉強でいうと、大学1年の線形代数と微分積分は間違いなく急所なのではないかと思っています。特に、線形代数は全般的に強敵で、高校の数学からは一転して急に難しくなり、腰を据えてよく理解しないとちんぷんかんぷんだったように思います。一方で、微分積分については、大部分は高校の内容の延長なのですが、$\epsilon-\delta$のところが、最大、かつ、ほぼ唯一と言っていい難所なのではないかと思っています。
- 異論がある方もいらっしゃるかも知れませんが、$\epsilon-\delta$のあたりを正確に理解できれば、それ以降のところは延長ですんなり理解できるという意味で、急所ではないのではないかという意味で書いています。
- (ちなみに、線形代数については、こちらの記事も宣伝させていただきます。)
ということで、この記事では、(私と同じように)大学1年の数学で挫折して長年数学コンプレックスに苦しむ方を撲滅すべく、$\epsilon-\delta$についてできる限り分かりやすく説明してみたいと思います。
ちなみに、世の中、数学好きの方も多いので、ツッコミを入れたい方も多いかも知れませんが、建設的なツッコミ・訂正は歓迎いたします。攻撃的なツッコミはご容赦いただけましたらと思います。
2. まず、ε-δはなぜ必要か?
まず、なにごとも、目的がよく分かっていないと理解をするやる気が出ないと思いますので、まずは、$\epsilon-\delta$がなぜ必要かを少し考えてみます。
2.1. ε-δが必要な例 〜 「連続」とは何か?
例として、「連続」について考えてみます。連続というのは、漠然とは、「線がつながっているもの」と理解できると思います。しかし、よく考えてみると、「線がつながっている」という表現は実はちょっと曖昧なのではないでしょうか?例えば、鉛筆で書いた線は連続でしょうか?一見つながっているように見えますが、どんどん拡大していくと、黒い粉が紙の上に無数に乗っているだけなので隙間があるかも知れませんよね?また、さらに細かく見ていくと、分子とか原子のレベルでは本当につながっていると言えるのでしょうか?そう考えると、「線がつながっている」というのは雰囲気で定義しているだけで、厳密な定義ではないことが分かります。実は、$\epsilon-\delta$を使うことより、「連続」というものが、言葉により厳密に定義をすることができるのです。これが、数学でいろいろなことを$\epsilon-\delta$を使って定義する目的なのではないかと思います。
2.2. 言葉で定義ができることのメリット
では、言葉を使って厳密に定義ができると何が嬉しいのでしょうか?私の理解では、言葉を使って厳密に定義ができることで、意思疎通を行う上での曖昧さがなくなるというメリットがあると思います。ちょっとよい例か分かりませんが、例えば、絵や写真、音楽などの題名が思い出せないときに、絵や音楽は言葉では表現することができないので検索するのに苦労すると思いますが、題名が分かっていれば、言葉として表現ができるため、検索が簡単にできると思います。言葉で定義ができることによるメリットはこれと同じことなのではないかと思っています。
実際、ものごとを正確に定義するために、自然科学関連の論文や教科書を読んでいると、たまに(それなりに頻繁で)、$\epsilon-\delta$を用いた表現は出てくるもので、このような表現が出てきたときに、ひるまないようにするために、$\epsilon-\delta$を理解しておくことはとても重要なのではないかと思います。(個人的には、$\epsilon-\delta$で表現されたものは、実はそんなに難しいものではなく当たり前のことを言っていることも多いように思いますが、論文などでは何事も正確に表現しなければならないため、$\epsilon-\delta$を使わざるを得ないのではないかとも思っています。)
3. ε-δの解読
とういことで、目的も分かりやる気も出たところで、次に、$\epsilon-\delta$の意味について、「連続」の定義を例に、順を追って理解をしてみることにします。
3.1. ε-δを用いた連続の定義
では、まずは、何はともあれ、$\epsilon-\delta$を用いた連続の定義を見てみます。関数$f(x)$が$x=x_0$で連続であるということは、$\epsilon-\delta$を用いて次のように定義されます。(この定義の意味をこの後解読して行きます。)
$$
\forall \epsilon>0, \exists \delta>0, |x-x_0|<\delta \Rightarrow |f(x)-f(x_0)|<\epsilon \tag{1}
$$
3.2. ε-δの理解の手順
個人的には、$\epsilon-\delta$の理解は、以下の2段階で行う必要があると思っています。
- $\epsilon-\delta$の記法を日本語に変換する
- 日本語の意味を理解する
3.2. ε-δの記法を日本語に変換する
実はここは機械的にできるのでそんなに難しくはないと思います。単に、
- $\forall$ ・・・「どんな〜についても」
- $\exists$ ・・・「〜が存在して」
と訳せば大丈夫です。ということで、まず、(1)を日本語に変換してみますと、
どんな$\epsilon>0$についても、$\delta>0$が存在し、$|x-x_0|<\delta$だったら$|f(x)-f(x\_0)|<\epsilon$
となります。
3.3. 日本語の意味を理解する
では、次に、上の日本語の意味を解読してみます。(上の定義は、日本語では書かれていますが意味はちんぷんかんぷんという感じだと思いますので。)
そのため、まずは、「連続」というののはどういうものか?ということを今一度考えてみます。
3.3.1. 不連続な関数の例を考えてみる
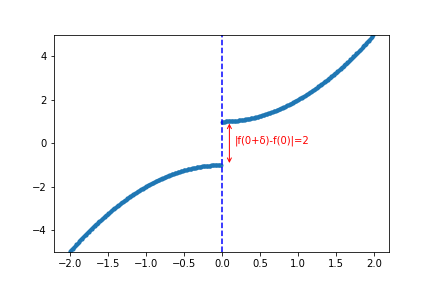
まずは、連続とはどいうものかという理解のきっかけをつかむため、以下のような、$x=0$で不連続な関数の例を考えてみます。
これは$x=0$付近で段差がある、つまり、|$f(x+\delta)-f(0)|=a$(今回の例では$a=2$)になってと言えます。(以下図もご参照ください。)
3.3.1. 連続な関数の例を考えてみる
次に、連続な関数を考えて見ます。例として、$f(x)=(x+2)^2-4$という関数の$x=0$付近の様子を見てみることにします。$x=0$付近で連続になっていますね。(線がつながっていますね.)
ちなみに、上のグラフは、以下のコードのように、$x$を0.01刻みでプロットしてみています。
def g(x):
y=(x+2)*(x+2)-4
return y
x=np.arange(-2, 2, 0.01)
y=g(x)
ymin=-5
ymax=5
xmin=-2
xmax=2
plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.scatter(x,y,marker='.')
ちょっと拡大してみてみます(グラフのスケールを変更してみます)。まあ、線はつながっていますね。
もっと拡大してみます。連続でなくなってしまいました。。まあ、$x$を0.01刻みで書いているので当たり前と言えば当たり前ですね。ただ、では、この関数は連続と言えるんでしょうか?
とりあえず、さらに拡大してみてみます(最初のグラフから100倍に拡大してみました)。先ほどの不連続のグラフの例と同様、$f(x)$の隣り合う点同士が離れてしまい、$|f(0+\delta)-f(0)|=0.04$となっています。ここで、$\delta=0.01$(グラフをプロットした時の刻み幅)です。
んー、これでは、連続とは程遠いですね。。ということで、刻み幅を先ほどの半分にして、0.005にしてグラフを書いてみましょう。
$|f(0+\delta)-f(0)|=0.02$になりました。では、さらに刻み幅を細かくして、$0.001$にしてみましょう。
だいぶ連続っぽく見えてきましたが、まだ間隔が空いている(つまり、$|f(0+\delta)-f(0)|$が大きい)ですね。
刻み幅をもう少し細かくして、0.0001にしてみましょう。
線がつながりましたね!(少なくとも見た目には)
以上、くどくどと書きましたが、以上から分かることは、
- 一見つながっていそうなグラフでも、実は拡大してみるとつながっていない。
- ただ、刻み幅を細かくすると、このような場合でも、つながったグラフを描くことが可能。
ということが分かりました。これを言い換えると、
- $|f(x+\delta)-f(x)|$がいくらでも小さくできるとき(つまりどんなに拡大しても、隣あう$f(x)$同士がつながっているとき)、連続であると言える。
- 連続な関数の時は、$x$の刻み幅(隣り合った$x$の同士の間隔)をどんどん小さくすれば、1を実現することができる。
ということが分かりました。
※ここで1点補足ですが、連続かどうかは、グラフの縦方向に隙間が空いているかどうかに注目をする必要があります。これまでの説明も、縦方向の隙間に注目して説明をしてきました。なぜならば、(最初に明示的に書くべきだったかも知れませんが)、$x$は実数(=連続)であると仮定しているため、グラフの横方向は、プロットの間隔をどんどん小さくしていけばいくらつなげられることは自明な前提としておいているからです。
3.3.2. さらに言い換えてみる
上記の表現をさらに言い換えてみると、以下のように言えます。
隣り合う$x$の間隔$\delta$をどんどん小さくしていけば、$|f(x+\delta)-f(x)|$はどんどん小さくすることできるとき、連続であると言える。
さらに言い換えると、
どんな小さな$|f(x+\delta)-f(x)|$も、$\delta$をどんどん小さくすれば実現できるとき、$f(x)$は連続である。
上の表現はどの点で連続かが書いてなく、ちょっと曖昧ですので、$x_0$で連続であることを正確に表すように書き方を変えてみると、
どんな小さな$|f(x)-f(x_0)|$も$|x-x_0|$をどんどん小さくすれば実現できるとき、$f(x)$は$x=x_0$で連続である。
と言えます。何度もくどくてすみませんが、さらに言い方を変えると、
どんな小さな$\epsilon>0$に対しても、$|x-x_0|<\delta$のようにすると、$|f(x)-f(x\_0)|<\epsilon$にすることができる
だんだん、$\epsilon-\delta$を使った定義に近づいてきましたね。もう一声変換すると、
どんな小さな$\epsilon>0$に対しても、$\delta>0$が存在し、$|x-x_0|<\delta$のようにすると、$|f(x)-f(x\_0)|<\epsilon$にすることができる
はい。3.2の日本語になりましたね。ということで、連続の定義を正確に表現しようとすると、$\epsilon-\delta$を使った定義になるということです。
4. 終わりに
できるだけ分かりやすく(疑問が発生しないまで詳細に)説明しようとしたつもりで書き始めましたが、ちょっとくどくなってしまったのと、結局なんだかんだで分かりにく説明になってしまったかも知れません。ただ、この説明だけでは理解できなかったとしても、他の説明を読んでよくわからないところやイメージが沸かないところを補う記事になってくれれば嬉しいかなと思っています。