実際のプログラミング演算に結びつけるまでにはまだまだ随分とかかりそうですが、とりあえずメモがてら。ちなみにエントロピー(Entropy)って中国語だと「熵」の1文字なんですね。なんだか痺れます。
エントロピー(Entropy)なる概念の二つの定義からの出発
「閉じた系(システム)においてはエントロピーが必ず増大する」とする「エントロピー増大の法則」は、しばしば「整理整頓された状態(秩序段階)から散らかった状態(無秩序段階)への移行」としてイメージされてきました。
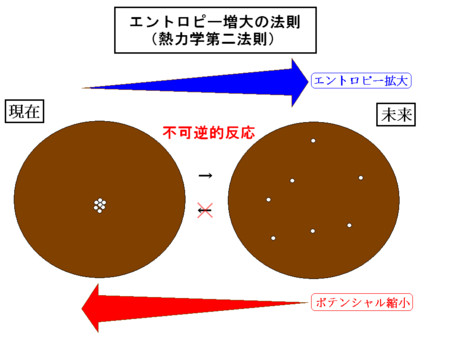

ここではあえて真逆に「散らかった状態(各地域文化が全く統合されてない段階)がエントロピー最小(すなわちあらゆる形で地域間交流が変化を引き起こす可能性が想定可能な状態)、全てが完全に整理整頓された状態(文化統合の結果、中央文化のみが残った段階)をエントロピー最大(すなわちもはや地域間交流が如何なる変化も引き起こさないある種の熱死状態)」とイメージし、その過程全体を「グローバリズムの進行」と捉えます。その志向性は「地域間差異の偏在」を克服しようとする動きとして始まり、全ての差異の消し込みに成功するとその役割を終える(熱的死状態を迎える)訳です。
人文学方面におけるエントロピー(Entropy)概念の援用
そう、ここで論じたいのは人文学方面へのエントロピー(Entropy)概念援用の為の定義整備なのです。
-
ゴビノー伯爵(Joseph Arthur Comte de Gobineau,1816年~1882年)の人種エントロピー論や(ポーランドの特権階層シュラフタ(ポーランド語:szlachta/ルーシ語:шляхта)擁護に端を発する)ニーチェ(Friedrich Wilhelm Nietzsche, 1844年~1900年)の(貴族論的)英雄主義やレヴィ=ストロース(Claude Lévi-Strauss、1908年~2009年)の構造主義的文化人類学といった「社団(Association=アソシアシオン)は実存する」なる前提に立脚するフランス社会学の伝統に分類される諸概念は、この意味合いにおける「グローバリズムの完成=あらゆる変化の源たる多様で多態な差異が失われた熱的死状態」への志向をニヒリズムの一種と捉え、徹底抗戦を誓う。
『ゴビノーの『人種不平等論』』
シュラフタ - Wikipedia
ただしゴビノー伯爵の人種エントロピー論がかかる志向性の展開を歴史的必然と見做す悲観主義(以下に述べるマンハイム分類における進歩主義)の立場に立つのに対し(すなわち、それ以上変化が起こらない熱的死状態の到来は不可避と考える)、ニーチェの英雄主義やレヴィ=ストロースの構造主義的文化人類学は「差異の温存こそが人類を(それ以上変化が起こらない熱的死状態の到来がもたらす)滅亡から救う」と考える楽観主義(マンハイム分類における伝統主義)の立場に立つ点が異なる。
【エントロピー理論の終着地点?】「距離のパトス」とメタ・レイシズム -
カール・マンハイム(Karl Mannheim,1893年〜1947年)「保守主義的思考(Das konservative Denken、1927年)」はまず「万物は(神の摂理を法源とする)自然法によって定められており、一切変えるべきではない」と考える中世的伝統主義が実存し、それに対して「数理的に抽出して改善を加える事が可能な次元では操作を遂行しよう」と提唱する楽観的進歩主義と「だが我々の数理抽出能力とその操作遂行能力はあくまで限られていて間違う事もあり、未知の変数を見逃してる可能性もあるから操作は慎重に進めるべき」と反論する悲観的保守主義が現れるが両者は表裏一体の関係にあり同一人物の中ですら共存可能とした。
【沈黙 -サイレンス-】【保守主義的思考】日本はシャトーブリアンがただの肉の呼称になってしまう国? - 一方英国政治学(英米法学)の伝統は薔薇戦争時代と清教徒革命時代から得た現実的教訓から「究極の自由主義は専制の徹底(すなわち反対意見の黙殺)によってのみ達成される」なる悲観主義に到達し「国家=暴力的解決手段の独占によってその処理遂行能力を担保された超越的裁定機関」が客観的に地域間紛争を裁定し裁定結果を守らせる「法実証主義(Legal Positivism)」を採用。
「究極の自由主義は専制の徹底によってのみ達成される」?
これが近代国家の枠組みの原型となったが、この理論において国家は原則として「数理的に抽出して改善可能な次元」のみを扱うと考えられるので、一応はマンハイムの分類においては楽観的進歩主義の一種と捉えられる。
法実証主義 - Wikipedia - 一方、中世から近世にかけて所領としては一定範囲を保ちつつ(純粋に国際情勢にのみ拠って外挿的に)王統だけが差し替え続けられた(ナポリやシチリア島を中心とする)南イタリアでは「国家は実存する」なる前提から出発して横軸に「(税収や兵役や賦役といった)国民負担」、縦軸に「(その見返りとしての)国家提供サービスに対する国民満足度」を取って国家経営の健全度を測定するイタリア経済学の伝統が発祥した。
イタリア経済学の伝統
これも一応は「国家は数理的に抽出して改善可能な次元のみを扱う」観点からマンハイム分類において楽観的進歩主義の一種に含め得るが、ここで現れる「国家が国民に強いる負担」や「見返りとして国民が国家に求めるもの」が「すべからく」数理的に抽出された改善操作を許すかどうかは随分と微妙な話題であり、実際「ここにムッソリーニのファシズムが付け込む余地があった」とユーロ・コミュニズムの父グラムシ(Antonio Gramsci、1891年~1937年)は反省しているのである。
「すべからく」の意味と類語、注意したい誤用と正しい例文5選 | マナラボ
【「諸概念の迷宮」用語集】ムッソリーニ VS グラムシ & ネグリ - こうした一連の考え方に対しドイツ社会学の伝統はマルクス主義元祖カール・マルクス(Karl Marx, 1818年~1883年)「経済学批判(Kritik der Politischen Ökonomie,1859年)」における「我々が自由意思や個性と信じ込んでいるものは、実際には社会の同調圧力に型抜きされ量産された既製品に過ぎない」提言や精神科医フロイト(Sigmund Freud,1856年~1939年)の神経症研究を通じて明かされた「人間の行動は思うより無意識や超自我の影響下にある」報告から出発する(当時の言説には実際「マルクス=フロイト主義」なる表現が見受けられる)。
「唯物史観」と「マルクス・フロイト主義」
この観点においてドイツ社会学の伝統は「人間の自由意志が純粋な形で顕現するのはいかなる制約も受けてない場合だけである」と考える立場から逆算して「それを実際には統制下に置いて拘束する超越的構造」を一つずつ炙り出してその相互関係について推察を加えるのである。
マックス・ウェーバーの「鋼鉄の檻理論」
このあたりの事情についてドイツ人作家ギュンター・グラス(Günter Grass, 1927年~2015年)の代表作「ブリキの太鼓(Die Blechtrommel, 1985年)」に「ドイツ人は魂で直接探すのを好むが、感覚器官でない魂が一体何を検出するというのだろう?(意訳)」なる(カントの観念論を告発する様な)鋭い懐疑を掲載している。ちなみにドイツのデュッセルドルフにユダヤ人として生まれ、後にフランスに亡命してパリでカソリック教徒として亡くなった詩人ハイネ(Christian Johann Heinrich Heine, 1797年~1856年)は「ドイツ近代文学の歴史のために(Zur Geschichte der neueren schönen Literatur in Deutschland, 1833年)の中で「五感が感受する官能、およびそれへの反応としての全身の運動器官の使用履歴の総体」として人間を理解しようとするフランス人の官能主義(行動主義)的伝統と「客観的経験論でなく主観的直観が人間を善導するイメージ」を重視するドイツ人の超絶主義(Transcendentalism=トランセンデンタリズム)的伝統を対比させていたりする。
【哲学ノート】カントの観念論 (人間学ブログ NINGENGAKU Blog)
ハインリヒ・ハイネ - Wikipedia
「精神と肉体の齟齬」の超克方法
超絶主義 - Wikipedia
全体的にゴチャゴチャしてるので整理を試みましょう。
- 文中で多用される「悲観的」「楽観的」なる形容詞は、それぞれの立場における観測原点(Ovservation Origin)に依存しており全体像を俯瞰する場合には切り捨てざるを得ない。
-
フランス社会学の伝統が立脚する方法論的集合主義(Methodological Collectivism)とドイツ社会学の伝統が立脚する方法論的個人主義(Methodological Individualism)の対峙についてはとりあえず$対象_n(n=個人 \rightleftharpoons 集団)$と単純化した次元として組み込み、フランス人の官能主義的伝統やドイツ人の超越主義的伝統などはかかる「数直線」上のしかるべき地点に配置されるものとする。
方法論的集合主義
方法論的個人主義 - Wikipedia - 英国政治学(英米法学)が立脚する法実定主義については、とりあえず上掲の対象次元に(それぞれの対象の存続可能性に影響する)$対象_n(n=マイノリティ(少数派) \rightleftharpoons マジョリティ(多数派))$なる評価軸の追加で対応する。ここで論じたいのはエントロピー増減に影響する部分だけなのでイタリア経済学の伝統の観点も含め全体を統制するのが自然競争状態であるのが正しいか、国家であるのが正しいかといった話題までは踏み込まない。
すると、ここで論じられているエントロピーが、数理的には以下の3種類のアプローチに大別可能である事実が浮かび上がってくるのです。
加法群(Additive Group)的アプローチ
任意の二点間の平均を求め続ける事で最終的に加法単位元(Additive Identity)0すなわち(熱的死状態に対応する)その系全体の平均値(分布の中心)に到達する流れ。
- ある意味、ゴビノー伯爵の人種エントロピー論そのものの実装。逆を言えばニーチェの英雄主義やレヴィ=ストロースの構造主義的文化人類学における「あえて演算を遂行しない事で結論への到達を回避する」伝統主義的態度は数理的には全く無意味となります。演算不可能なら最初から演算そのものが遂行不可能ですし、演算可能なら演算結果は自明の場合(Trivial Case)として勝手に算出されるだけの話。
- 統計学上、データセットの平均から中心を割り出すプロセスに対応します。
【数理考古学】群論とシミュレーション原理⑧族の分類とそれに下属する演算集合の関係の整理
【初心者向け】平均と標準偏差、中央値と平均偏差
【初心者向け】標本分散と不偏分散
【初心者向け】度数分布(Frequency Table)/度数分布図と最頻値(Mode)
【初心者向け】記述統計学と代表値
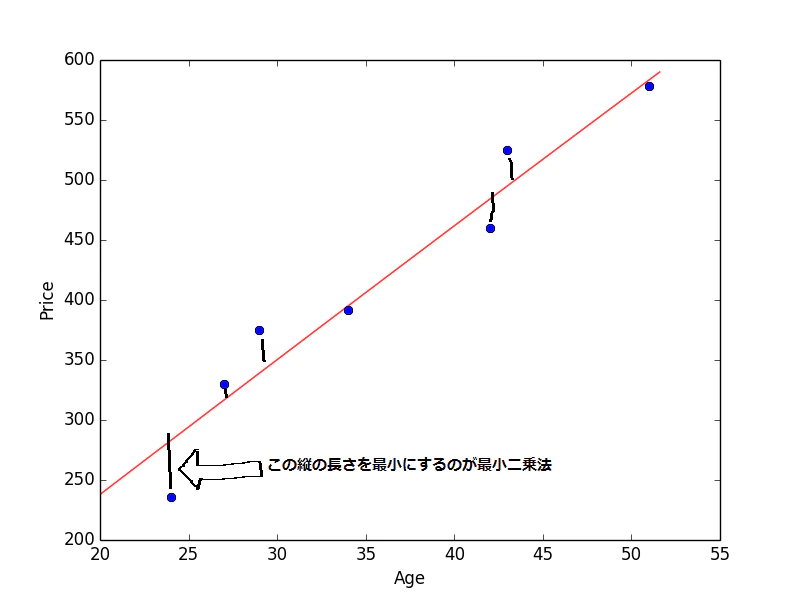
線形回帰とは何か - Qiita
乗法群(Multiplicative Group)的アプローチ
とりあえず乗法単位元(Multiplicative Identity)1をエントロピー最小の状態と考え、実態がこれから離れるほどエントロピーが増大していくとみなす。さしあたって結果として実態が到底乗法単位元1の近似とは見做せなくなった時点で(その状態への復元が絶望的となった段階で)熱的死状態を迎えると考える。
- どうやら英国政治学(英米法学)における法実定主義の運用的制度診断やイタリア経済学における国家経営状態の健全性診断に対応する様で、さらに制御工学(Control Engineering)におけるフィードバック理論の諸概念を追加する事で様々な発展系が考えられそうです。
制御工学 - Wikipedia -
ロジスティックス方程式(Logistic Equation)などを用いたアプローチとも相性が良さそうです。
【初心者向け】ロジスティック方程式とその関連範囲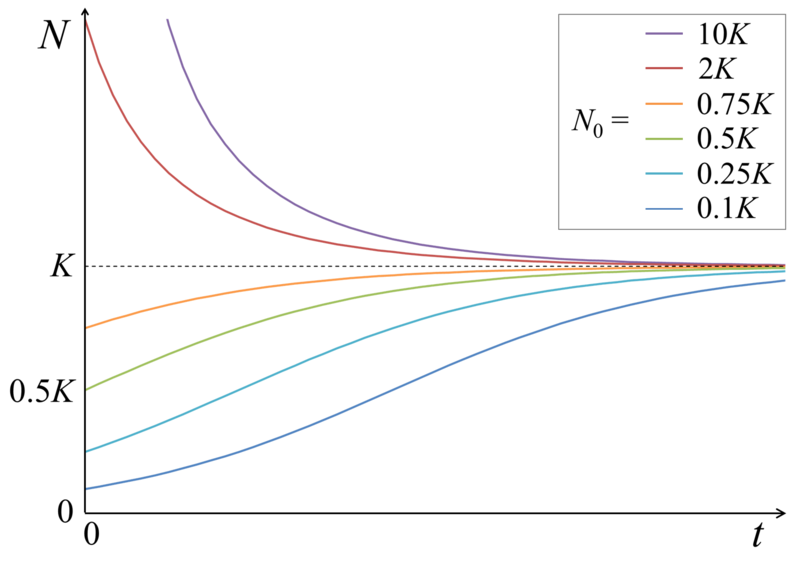
- という事は「テクノスリラー」ジャンルを創設した小説家マイケル・クライトン(Michael Crichton、1942年~2008年)が「ウエストワールド(Westworld,1973年)」や「ジュラシック・パーク(Jurrassic Park,1990年)」で扱った「(カオス過程進行による)テーマパークの暴走」の様な観点もこの分類に含まれる事になりますね。
ロジスティック写像 - Wikipedia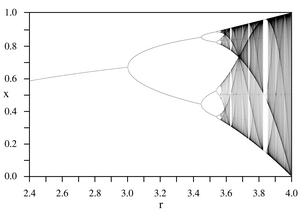
統計学的境界線(Statistical Boundaries)
統計学(Statistics)的には、その分布が有意水準++(Significance Level)を満たさない=帰無仮説(Null Hypothesis)を棄却**(Rejection)出来ない=サンプル数過剰などによってその分布が個性を喪失し正規分布(Normal Distribution)などの大数の法則的一般分布に併呑される展開を熱的死状態を迎えたと考える流儀も存在する。
- 一見、上掲の設問では扱わなかった存在論(Ontology)と関係してきそうに見えます。
存在論 - Wikipedia - しかし実際の数理的アプローチはかかる形而上学的側面に踏み込む事なく、例えば「**フーリエ級数による特定波形の近似は何処から何処まで有効か?」といった話題に進んでいくのです。
【初心者向け】フーリエ解析(Fourier Analysis)を可視化する。



- また 「その画像に写っているのが猫と分かる為には如何なる特徴抽出が有効か」といった機械学習的側面に進んでいく事も想定されます。
その呼称は1959年にアーサー・サミュエルによって造語された。
トム・M・ミッチェルによる定義
コンピュータプログラムがタスクのクラスTと性能指標Pに関し経験Eから学習するとは、T内のタスクの性能指数Pで測った性能が経験Eにより改善される事を言う。
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E。
- タスクとは、プログラムが解くべき課題を指す。例えば売上予測タスクであれば「明日の売上を予測する」といった課題設定がタスクとなる。
- 経験はなんらかのデータとしてプログラムに与えられ、それを訓練データもしくは学習データと呼ぶ。売上予測タスクなら例えば「過去の経験=今日までの売上」が訓練データとして与えられ、それを用いてプログラムの性能を改善する過程を、「プログラムを訓練する」もしくは「プログラムを学習させる」と呼ぶ。またプログラムの訓練に用いられるデータ全体の集合を(訓練もしくは学習)データセット(データ集合とも)と呼ぶ。
- 性能指標は、プログラムがタスクをどの程度の性能で達成したかを測る指標で、前述の売上予測タスクであれば、例えば実際の売上との誤差を性能指標として用いる事ができる。
こうして全体像を俯瞰すると乗法群的エントロピー制御の一種として組み込まれる形となりそうです。
人文学上の諸概念と数理の対応
上掲の諸概念は統計学や制御工学上の諸概念の爆発的発展が始まる以前にその定義が固まり、以降ちゃんとした形でアップデートされずにきました。ましてや以下ほど新しい概念となると…
ドイツの物理学者ルドルフ・クラウジウス(Rudolf Julius Emmanuel Clausius, 1822年~1888年)が、カルノーサイクルの研究をする中で、移動する熱を温度で割ったQ/Tという形で導入され、当初は熱力学における可逆性と不可逆性を研究するための概念であった。後に原子の実在性を強く確信したオーストリアの物理学者ルートヴィッヒ・ボルツマン(Ludwig Eduard Boltzmann, 1844年~1906年)によって、エントロピーが原子や分子の「乱雑さの尺度」であることが論証された。
クラウジウスは1854年にクラウジウスの不等式として熱力学第二法則を表現していたが、彼自身によって「エントロピー」の概念が明確化されるまでにはそれから11年を要した。不可逆サイクルでゼロとならないこの量をクラウジウスは仕事と熱の間の「変換」で補償されない量として、1865年の論文においてエントロピーと名付けた。エントロピーという言葉は「変換」を意味するギリシア語: τροπή(トロペー)に由来する。
その後ボルツマンやギブス(Josiah Willard Gibbs, 1839年~1903年)によって統計力学的な取り扱いが始まった。情報理論(直接的には通信の理論)における情報量の定式化が行われたのはクロード・シャノン(Claude Elwood Shannon,1916年~2001年)の1948年『通信の数学的理論』においてとなる。シャノンは熱統計力学とは独立に定式化にたどり着き、エントロピーという命名はフォン・ノイマン(ハンガリー語:Neumann János/独:John von Neumann, Margittai Neumann János Lajos, Johannes Ludwig von Neumann,1903年~1957年)の勧めによる、と言われることがあるが、シャノンはフォン・ノイマンの関与を否定している。
まぁ大体上記の様に考えておけば現代でも大体通用しそうです。そんな感じで以下続報…




