こんにちは。LiNKX株式会社のitoです。
このブログは、以下のシリーズの(2)となります。
- 異常検知(1)確率分布による基本の異常検知
- 異常検知(2)ガウス分布を仮定する異常検知、ホテリングのT2法 <----- このブログ
- 異常検知(3)データがガウス分布から外れていても使える、k近傍法
- 異常検知(4)時系列信号の変化の検知、特異スペクトル変換法など
- 異常検知アルゴリズムの評価方法 ROCAUC を分かりやすく説明
- 深層異常検知(1)Gaussian-AD; 学習時間ほぼなしの高性能異常検知アルゴリズム
※このブログは、会社の考え方ではなく私個人の解釈です。もし、私の思い込みで間違った解釈や記述がありましたら、ご指摘いただけると幸いです。
前回の異常検知(1)をまとめると、
「正常の観測値の分布$p({\bf x})$が分かっている場合、異常度は $a({\bf x}) = - \log p({\bf x})$ で表せます」
という内容でした。
しかし、通常は、真の$p({\bf x})$は分かりません。しかし、近似の分布$p'({\bf x})$を作ることができれば、それらしい異常度を$a({\bf x})=-\log p'({\bf x})$として作ることができます。この回は、真の確率分布をガウス分布で近似して異常度を求める、「ホテリングの$T^2$法」を紹介します(参考文献 [1])。
ただし、ホテリングの$T^2$法では、閾値の求め方も提案していますが、ここのブログではその方法にはふれません。異常度を求めるところまでの内容になります。
以降、以下の流れで進めます。
1. 異常検知の問題の定義
使用する変数と異常検知の問題を定義します。
まず、D次元の観測データを考えます。1回の観測データを以下の縦ベクトルで表します。インデックスはプログラムと合わせるために、0から始まりとします。
{\bf x} =
\begin{bmatrix}
x_0 \\
x_1 \\
\vdots \\
x_{D-1}
\end{bmatrix}
正常値として観察されたこのような観測データが$N$個あるとし、右肩のカッコの数字でデータのインデックスを表すことにします。それをまとめて $D$ とします。
D = \{ {\bf x}^{(0)}, {\bf x}^{(1)}, \cdots, {\bf x}^{(n)}, \cdots, {\bf x}^{(N-1)} \}
ここで、異常検知の問題を、
「この正常値の観測データ $D$ を使って、新しい観測${\bf x}$ に対する異常度 $a({\bf x})$を求める式を作りなさい。」
とします。異常度が分かれば、閾値を設定して、異常値がその閾値を超えたときに「異常」という警告を出すことができます。
2. ホテリングのT2法の概要
分布とデータ
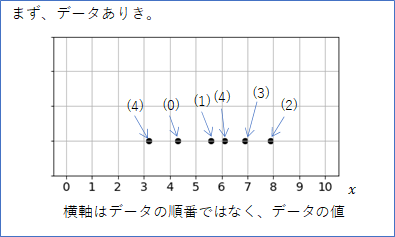
まず、簡単のため下図のような1次元の観測データ6個$x^{(0)}, \cdots, x^{(5)} $だけを考えます。横軸はデータの順番ではなく、データの値であることに注意してください。
このような、予測できない曖昧さ(ノイズなど)を含んだデータは、「何らかの確率分布から生成されたもの」と考えると見通しが良くなります。
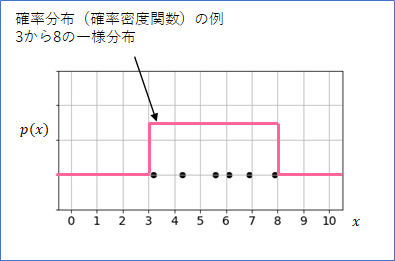
例えば、下の図の赤線は「3から8の一様分布」という確率分布1を表しています。この確率分布は、「データを3から8の間で等確率で生成」することができる分布なので、6個のデータはこの確率分布から生成されたとも考えることもできます。
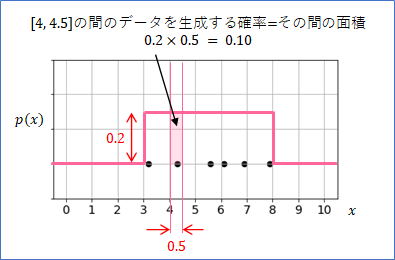
ここで、確率分布の正確な意味を説明したいと思います。今、下の図のように、[4, 4.5]のところで2本の縦線を引いたとします。この時、この2本の線とグラフに囲まれた領域の面積を考えることができます。
今、グラフの高さは$0.2$としており、よって、面積は、$0.5 \times 0.2 = 0.1$ となります。この値が、「[4, 4.5]の間にデータが生成される確率」となります。今考えている確率分布のグラフは高さが一定なので、[3, 8]の間では平等に(一様に)データが生成されることになります。
この確率分布で生成されるデータは、必ず3から8の間です。ですので、[3, 8]の間でデータが生成される確率は1です。つまり、[3, 8]の間のグラフの面積は1にならなくてはいけません。その理由から、このグラフの高さが0.2なのです$(0.2 \times (8-3) = 1)$。
しかし、通常はデータが生成された確率分布は分かりません。もしかしたら、下のような三角の確率分布(高さは適当に書いています)から生成されたのかもしれません。
この三角の確率分布だと、確率分布の定義から、8に近い数値ほど生成される確率が高くなります。しかし、あくまでも確率のことなので、そのような偏りが一見みられないようなデータが生成される場合も十分にありえます。
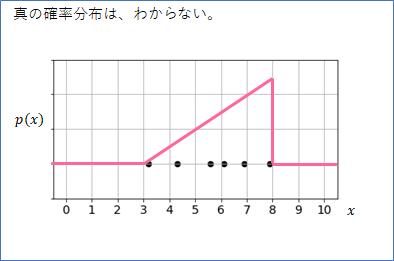
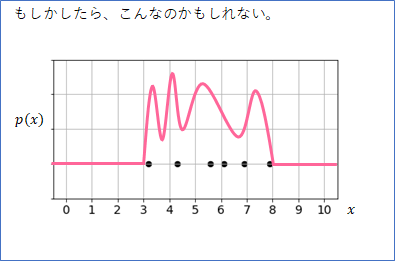
確率分布はシンプルな形をしているとは限りません。下のような、変な形の確率分布からこのデータは生成されたという可能性も無きにしも非ずです。
しかし、とにかく、データの背後にはこのような確率分布(確率密度関数)があり、その「真の確率分布からデータは生成された」、と考えるのがポイントです。そして、データがあればあるほど、真の確率分布の形は見えてきますので、良い近似の分布が作れるようになります。
そして、この真の分布$p({\bf x})$の近似の分布$p'({\bf x})$を作ることができれば、異常度は$a({\bf x})=-\log(p'({\bf x}))$で作れるので(異常検知(1)参照)、問題解決ということになります。
ガウス分布をフィッティング
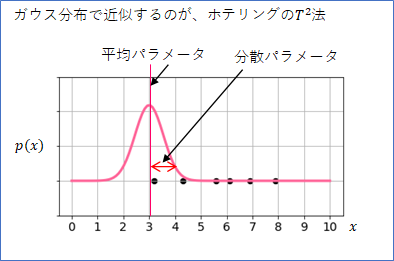
真の分布はわからないけれど、とりあえず、「ガウス分布で近似してみよう」、というのがホテリングの$T^2$法です。ガウス分布は下図のように、釣り鐘のような形をした分布です。身長の分布や、成績の分布など、ガウス分布は様々な現象で表れる分布なので、真の分布がうまくガウス分布に合う可能性は大いにあるでしょう。
ただし、多くの確率分布のモデル(数式化した確率分布)がそうであるように、ガウス分布にも、分布の形をチューニングするためのパラメータがあります。分布の中心を決める「平均パラメータ$\mu$」と、分布の広がりを決める「分散パラメータ $\sigma^2$」の2つです。
この2つのパラメータは、観測データから決めることができます。
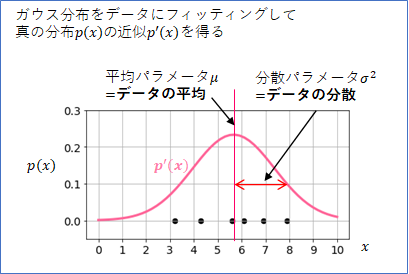
平均パラメータ$\mu$はデータの平均、分散パラメータ$\sigma^2$はデータの分散にセットすれば、ガウス分布は、データに最も合うように、チューニングされます(具体的な方法は「1次元データのホテリングの$T^2$法」で述べます)。この操作を、「データにガウス分布(モデル)をフィッティングする」と言います。
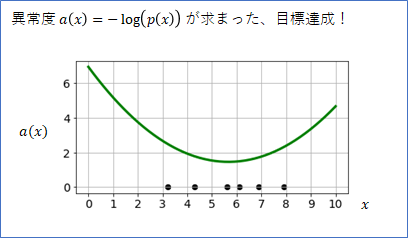
このフィッティングができれば、データの真の確率分布$p(x)$の近似分布$p'(x)$ を手に入れたことになりますので、そこから$a(x)=-\log(p'(x))$で異常値を決定すれば目標達成となります。
ところが、実はもっと簡単に$a(x)$ (の代用品)を求める方法があります。これが、ホテリングのT2法の偉いところの1つだと思います。
ここまでの手順を整理すると、以下のようになります。
(1) ガウス分布の平均パラメータ$\mu$と分散パラメータ$\sigma^2$ を決める
(2) $\mu$と$\sigma^2$から$p'(x)$を計算
(3) $p'(x)$から$a(x)$を計算
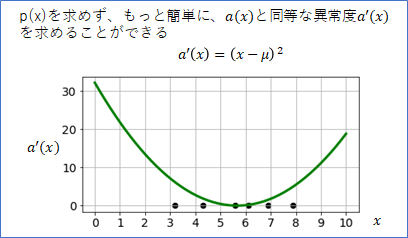
この手順を次のように簡単にします。
まず、(1)の$\sigma^2$を求めるのを省略します。(2)はまるまる省略します。(3)で、$a(x)$の代用品として $a'(x)$を以下のように定めます。まとめると以下のようになります。
(1) ガウス分布の平均パラメータ$\mu$を決める
(2) ---
(3) $a'(x) = (x - \mu)^2$
下が、$a'(x)$ のグラフです。$a(x)$とは、縦軸の倍率と上下の位置がことなりますが、中心の位置やグラフの広がり方は同じです。つまり、閾値を調節すれば、異常度としての$a'(x)$と$a(x)$の性能は同じです。
このように、背後の概念として$p(x)$はあるのですが、$p'(x)$を計算することなしに直接$a'(x)$を求めてしまう方法こそが、ホテリングの$T^2$法です。データが1次元の場合で考えましたが、多次元でも基本的には同じ流れになります。ただし、多次元データの場合は$\sigma^2$に対応するパラメータの計算は必要になってきます。
以上で概要の説明は終わりです。
3. 1次元データのホテリングのT2法
ここでは、少し数学とプログラムを使って、どのようにして前章の異常度$a'(x)$が出てきたかを説明します。そのあとで実際にPythonで異常度$a'(x)$を計算します。数学とプログラムが好きな方はぜひ読み進めてください。
異常度の導出
まず、1次元のガウス分布の具体的な式は以下のようになります。
p(x) = \frac{1}{\sqrt{2\pi \sigma}}\exp \Bigl(-\frac{(x-\mu)^2}{2 \sigma^2}\Bigr)
ここで、$\mu$は平均パラメータ、$\sigma^2$ は分散パラメータです。
平均パラメータ$\mu$は、データの平均値にセットします。
\mu' = \frac{1}{N}\sum_{n=0}^{N-1} x^{(n)}
分散パラメータ$\sigma^2$は、データの分散にセットします。
\sigma'^2 = \frac{1}{N}\sum_{n=0}^{N-1} (x^{(n)} - \mu')^2
異常度は、以下のようになります。
a(x) = -\log(p(x)) = -\log \Bigl( \frac{1}{\sqrt{2\pi \sigma'}}\exp \Bigl(-\frac{(x-\mu')^2}{2 \sigma'^2}\Bigr)\Bigr)
$a(x)$は、その閾値を調節すれば、掛け算されている定数を省略しても、足し算されている定数を省略しても、使用上の問題はありません。そこで、上の式を計算し、余計な定数を除くと、以下の異常度 $a''(x)$が得られます。
a''(x) = \frac{(x-\mu')^2}{\sigma'^2}
さらに、$\sigma'^2$ がなくても$a''(x)$の倍率が変わるだけなので省略できます。これが概要で出てきた$a'(x)$でした。
a'(x) = (x-\mu')^2
Pythonで異常度を計算
では、ここまでの関数をPython のプログラムで描いて確認します。プログラム環境は、google colaboratory を想定します。
必要なライブラリをインポートし、観測データをxsに作成します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
plt.rcParams["font.size"] = 14 # グラフのフォントサイズ調整
xs = np.array([3.2, 4.3, 5.6, 6.1, 6.9, 7.9]) # 観測データ
平均パラメータと分散パラメータをデータから決め、ガウス分布Px ($p(x)$)を作成します。
mu_prm = np.mean(xs) # 平均パラメータ
sigma2_prm = np.cov(xs) # 分散パラメータ
reso =50 # グラフの解像度
x_range=[0, 10] # 表示範囲
xxs = np.linspace(x_range[0], x_range[1], reso) # 表示用 x
Px = multivariate_normal(mu_prm, sigma2_prm).pdf(xxs) # ガウス分布
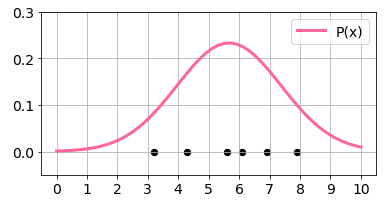
Px ($p(x)$)とデータxsのグラフを表示します。
# グラフ表示
def show_dat():
plt.figure(figsize=(6,3))
plt.scatter(xs, np.zeros_like(xs), s=40, c='k')
plt.grid(True)
plt.xlim(-0.5, 10.5)
plt.xticks(range(0, 11))
show_dat()
plt.ylim(-0.05, 0.3)
plt.plot(xxs, Px, color='#FF6699', lw=3, label='P(x)')
plt.legend()
plt.show()
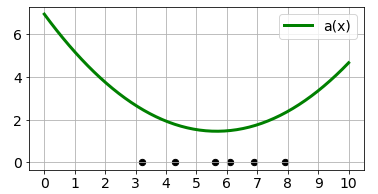
この$p(x)$から$a(x)=-\log(p(x))$で異常度を求めると以下のようになります。
Ax = -np.log(Px)
show_dat()
plt.plot(xxs, Ax, color='g', lw=3, label='a(x)')
plt.legend()
plt.show()
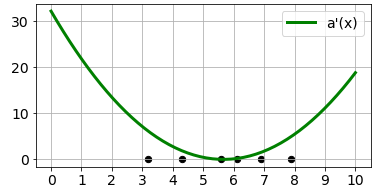
もっと簡単に求まる$a'(x)$は以下のようになります。
Ax2 = (xxs - mu_prm)**2
show_dat()
plt.plot(xxs, Ax2, color='g', lw=3, label="a'(x)")
plt.legend()
plt.show()
4. 2次元データのホテリングのT2法
ここまでは、1次元のデータ$x$で考えましたが、データが2次元${\bf x}=(x_0, x_1)^T$だったらどうなるでしょうか($T$は縦ベクトルであることを表します)。2次元のガウス分布を考えることになりますが、2次元ガウス分布は、1次元ガウス分布に比べると少し複雑なので、実際に問題を扱う方は2次元の場合も確認しておいた方がよいでしょう。2次元を確認すれば3次元以上はだいたい同じです。
まず、簡単に2次元のガウス分布を説明してから、ホテリングの$T^2$法を説明し、そのあとで、プログラムによる確認を行います。
2次元ガウス分布
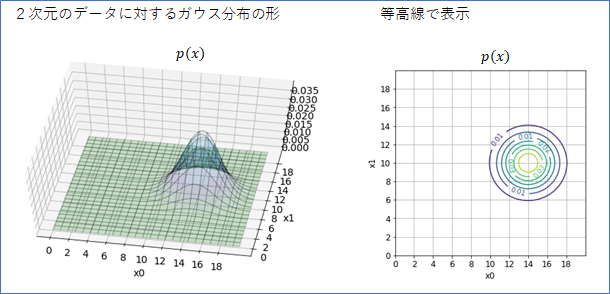
2次元データ用のガウス分布は、下の図に示したように、山のような形をしています。
右図のように等高線で表すと、その中心や広がり具合がはっきりわかります。1次元の時には全面積が1であったように、2次元の確率分布の場合は、山の体積が1となります。
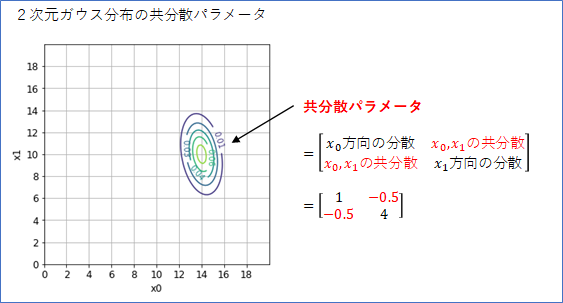
2次元のガウス分布のパラメータは、「平均パラメータ」と「共分散パラメータ」があります。1次元のガウス分布と比べるとちょっと複雑になります。
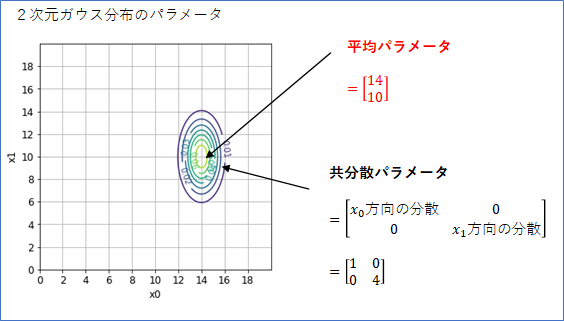
まず、「平均パラメータ」は、分布の中心位置を表しますが、$(x_0, x_1)$平面での位置を表すことになるので、2次元ベクトルになります。下の例では、平均パラメータを$\boldsymbol{\mu}=(14, 10)^T$としたときのガウス分布です。確率分布の中心が、座標$(14, 10)$にあることが分かります。
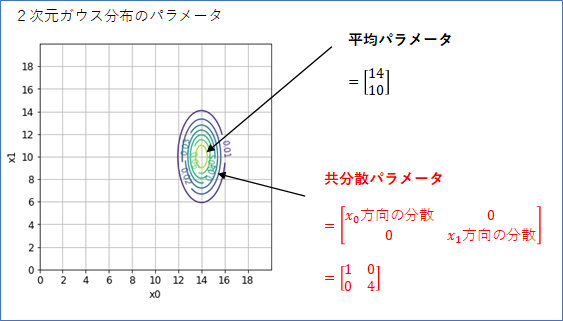
広がりを表すパラメータは、1次元ガウス分布の場合は「分散パラメータ」でしたが、2次元ガウス分布の場合は、「共分散パラメータ」となり、2x2の行列になります。ここがちょっとややこしいところです。
下の式のように、行列の[0, 0]成分が$x_0$の方向の広がり(分散)を表し、[1, 1]成分が$x_1$の広がり(分散)を表します。値が大きいほど広がりは大きくなります。この例では、[1, 1]に4と大きな値を指定しているので、$x_1$方向の広がりが大きくなっています。
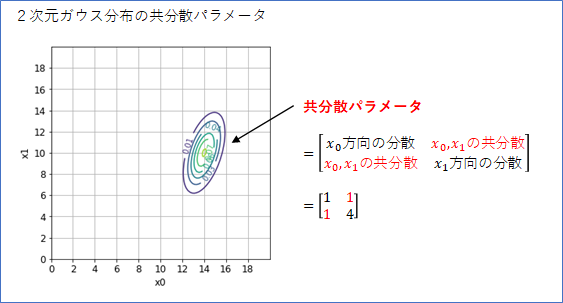
広がりパラメータの行列の[0, 1]成分と[1, 0]成分は、$x_0$と$x_1$の相関関係(共分散)の指定になります。この2つの成分は同じ値でなくてはいけません。$x_0$が大きい値をとるとき$x_1$も大きい値をとる傾向があるとすれば、共分散は正の数値になります。例えば、ここを1に設定すると、分布は右上がりになります。
行列の[0, 1]成分と[1, 0]成分を負の値にすると、負の相関、つまり、$x_0$が小さいとき$x_1$が大きくなる傾向を指定したことになります。例えば、-0.5を設定すると下のような分布になります。
以上が2次元ガウス分布の概要でした。
2次元データのホテリングのT2法
では、1次元と同じ要領で$a({\bf x})$を作っていきます。また、数式を使って進めていきます。
まず、${\bf x}$が2次元以上のガウス分布は、少し形が複雑ですが以下の式で表されます(今は2次元データを考えるので$d=2$です)。
p({\bf x})=
\frac{1}{(\sqrt{2 \pi})^d \sqrt{|\boldsymbol{\Sigma}|}} \exp\Bigl( -\frac{1}{2} ({\bf x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} ({\bf x}-\boldsymbol{\mu})\Bigr)
右辺の$\exp$の右側の分数は、分布全体の体積を1にするためのつじつま合わせの定数(つまり1つの数値)なのであまり気にする必要はありません。$\exp$の右のカッコの中は、ベクトルと行列の演算になっていますが、計算すると$x$の2次関数(2次形式)になります。つまりスカラーです。
このガウス分布がデータに合うように、パラメータをセットします。
平均パラメータ$\boldsymbol{\mu}$(2次元ベクトル)は、1次元のときと同様、データの平均値にセットします。
\boldsymbol{\mu'} = \frac{1}{N} \sum_{n=0}^{N-1} {\bf x}^{(n)}
共分散パラメータ$\boldsymbol{\Sigma}$(2x2行列)は、データの共分散行列にセットします。ここは、2次元ガウス分布のところで登場した2x2の共分散パラメータを、データから求めていることになります。
{\bf \Sigma'} = \frac{1}{N} \sum_{n=0}^{N-1} ({\bf x}^{(n)} - \boldsymbol{\mu'})({\bf x}^{(n)} - \boldsymbol{\mu'})^T
2次元のガウス分布の式$p({\bf x})$から異常度$a({\bf x})=-\log(p({\bf x}))$を計算して、余計な定数を除去すると以下の式になります。
a({\bf x})=({\bf x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} ({\bf x}-\boldsymbol{\mu})
つまり、ここに、上で求めたパラメータ$\boldsymbol{\mu'}$と${\bf \Sigma'}$をセットすれば、異常度$a({\bf x})$が求まり、目的達成です。
a({\bf x})=({\bf x}-\boldsymbol{\mu'})^T \boldsymbol{\Sigma'}^{-1} ({\bf x}-\boldsymbol{\mu'})
これが、2次元データの場合のホテリングの$T^2$法でした。
Pythonで異常度を計算
では、Pytonで異常度を計算してみます。ここでは、ポイントとなるPythonのコードのみを紹介します。
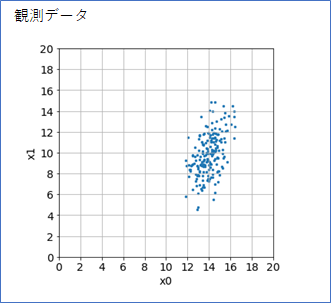
観測データが以下のように$x_0$と$x_1$に正の相関のあるデータ200点を考えます。
これは、numpyのrandom.multivariate_normalを使って以下のようにして生成したものです。これは、平均パラメータmeanと、共分散パラメータcovを、以下の数値で指定して、このパラメータを持つ2次元ガウス分布を「真の確率分布」としてデータxsを生成していることになります。
mean = np.array([14, 10])
cov = np.array([[1, 1],[1, 4]])
xs = np.random.multivariate_normal(mean, cov, size=200)
平均パラメータをデータから求めて、Muとします。データ生成時に設定した真の分布の平均パラメータに近い値が求まっています。
# 真の分布の値は [14, 10]
Mu = np.mean(xs, axis=0)
print(Mu)
# [13.969 9.853]
共分散パラメータを求めて、Sigmaとします。これも、データ生成時に設定した真の分布の共分散パラメータに近い値が求まっています。
# 真の分布の値は、[[1, 1],[1, 4]]
Sigma = np.cov(xs, rowvar=False, bias=True)
print(Sigma)
# [[0.929 0.937]
# [0.937 4.005]]
Sigma の逆行列 $\boldsymbol{\Sigma}^{-1}$ を求めてSigma_invとします。
Sigma_inv = np.linalg.inv(Sigma)
print(Sigma_inv)
# [[ 1.409 -0.33 ]
# [-0.33 0.327]]
分布中心の${\bf x}=(14, 10)^T$の異常度は、以下の計算で0.0053と求まりました。異常ではないパラメータ領域なので、0に近い値です。
x = np.array([14, 10])
a = (x - Mu) @ Sigma_inv @ (x - Mu)
print(a)
# 0.005376907789804893
分布中心から少し外れた${\bf x}=(12, 10)^T$の異常度は、5.66と求まりました。異常度が大きくなり、もっともらしい結果です。
x = np.array([12, 10])
a = (x - Mu) @ Sigma_inv @ (x - Mu)
print(a)
# 5.657417707878218
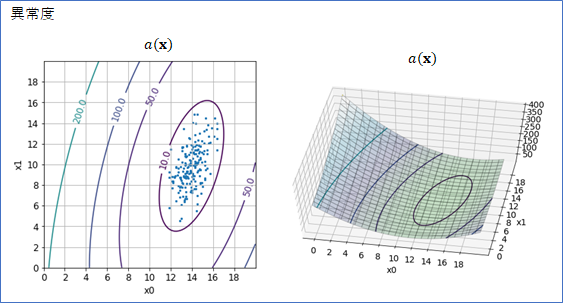
パラメータ平面で異常度を求めて等高線と3Dグラフを描くと以下のようになりました。ちょうど、データが分布しているところで異常値が小さくなっておりもっともらしい結果と言えます。
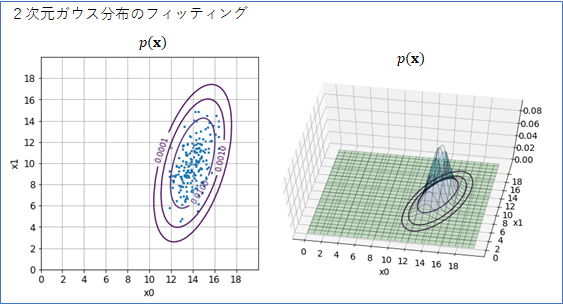
異常値の計算には必要ありませんが、求めたパラメータMuとSigmaで2次元ガウス分布がどのようにフィッティングされるかも可視化してみました。いい感じです。
5. さいごに
これで今回の異常検知(2)はおしまいです。最後までお読みいただきありがとうございました。
今回の方法は、データがガウス分布に近い場合には精度の高い異常度を計算できますが、そうでない場合は、精度が悪くなるので注意が必要です。
次の異常検知(3)は、データがガウス分布でない場合でも適用できる「近傍法」の説明をしたいと思います。
参考文献
[1] 井出・杉山著「異常検知と変化検知」機械学習プロフェッショナルシリーズ(講談社)
-
正確には、確率密度関数と言いますが、本ブログでは簡単のため確率分布と言うことにします。 ↩