異常検知アルゴリズムの評価方法 ROCAUC を分かりやすく説明

こんにちは。LiNKX株式会社のitoです。

異常検知のシリーズとして（４）まで紹介させていただきましたが、次からはディープラーニングを使った異常検知を紹介していきたいと思っています。論文などで提案されるアルゴリズムは、ベンチマークとしてのデータセットに対してROCAUCという指標で評価することが一般的です。そこで、このブログではディープラーニングに進む前段階としてROCAUCを紹介したいと思います。

ROCAUCを分かりやすく説明しているweb記事も多くありますが、その多くは確率分布の関数やその面積で説明しています。グラフをイメージすることが得意な方には、分かりやすい説明なのですが、グラフの苦手な方には少しややこしいかもしれません。

そこで、このブログでは、分布関数の図は使わずに「単なるプロット図」でROCAUCを説明しました。この方法はグラフが苦手な方でも直感的に分かりやすいのではないかと思います。是非読んでみてください。

※このブログは、会社の考え方ではなく私個人の解釈です。もし、私の思い込みで間違った解釈や記述がありましたら、ご指摘いただけると幸いです。

過去の異常検知ブログはこちら

• 異常検知（１） 確率分布による基本の異常検知
• 異常検知（２）ガウス分布を仮定する異常検知、ホテリングのT2法
• 異常検知（３）データがガウス分布から外れていても使える、k近傍法
• 異常検知（４）時系列信号の変化の検知、特異スペクトル法など
• 異常検知アルゴリズムの評価方法 ROCAUC を分かりやすく説明 <----- このブログ
• 深層異常検知（１）Gaussian-AD; 学習時間ほぼなしの高性能異常検知アルゴリズム

1. 異常検知アルゴリズム

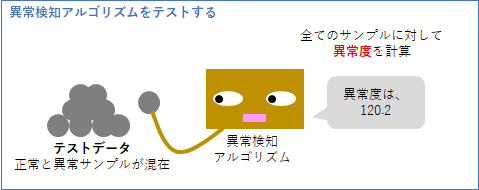
異常検知アルゴリズムの仕事は、「入力データに対して異常度という数値を出力すること」です。正常のデータに対しては異常度は小さく、異常のデータに対しては異常度は大きく出力することが理想です。異常度については、「[異常検知（１）] (https://qiita.com/makotoito/items/130b756473caa978f4ca)」でも説明していますので、そちらもご参照ください。

この異常検知アルゴリズムの性能を定量評価するために、正常と異常のサンプルが混在したテストデータを準備します。

このテストデータすべてに対して、アルゴリズムに異常度を計算してもらいます。当然、テストデータのラベル（正常か異常か）は見せません。

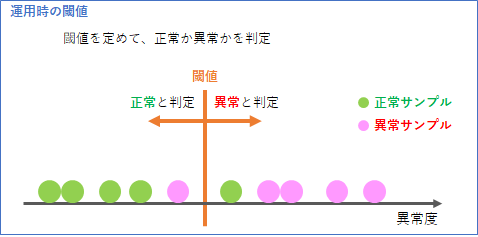
全てのサンプルに対して異常度の計算が終わったら、その異常度に従って、下の図のようにサンプルを並べます。ここで、正常と異常のラベルも明らかにします。

このアルゴリズムを運用するときには、どこかよさそうなところに閾値を設定し、入力データの異常値が閾値よりも低かったら「正常」、高かったら「異常」と判定することになります。

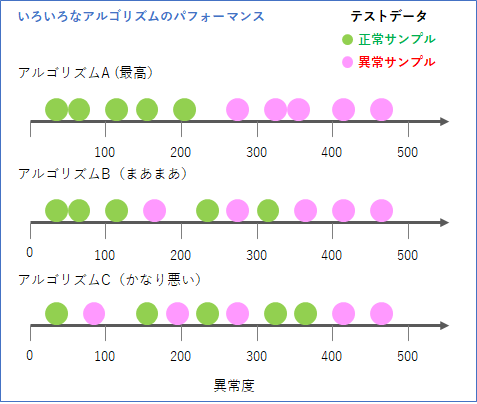
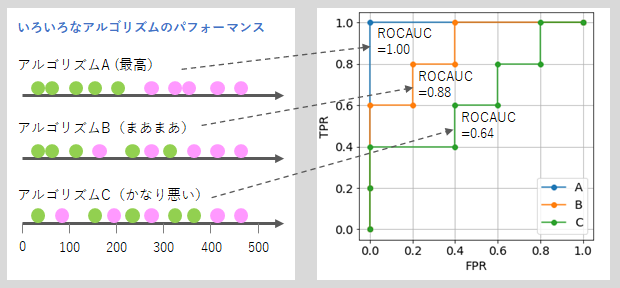
よって、正常と異常のサンプルが完全に左右に分かれれば、その間に閾値を設定することで、100点の異常判定ができます。これが下の図のアルゴリズムAです。

しかし、実際にはそうはいかなく、アルゴリズムBやアルゴリズムCのように、真ん中付近で、正常と異常のサンプルが混在することになります。この混じる程度が多ければ多いほど、異常検知としての性能は悪くなっていきます。

この混じり具合を異常検知の観点から定量的に表すのが、ROCAUCとなります。
そのために必要な概念としてTPRとFPRを説明します。

2. 正解の割合、True Positive Rate (TPR)

異常検知で最も重要なのは、「異常をどれくらい正しく検出できるか」という「正解の割合」です。

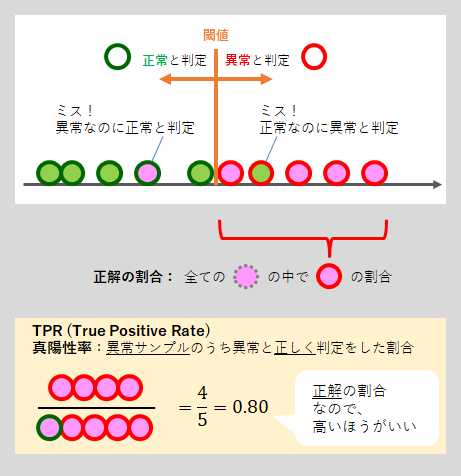
下の図のサンプル（円）の中の色は「ラベル」を表しています。「黄緑」は「真の正常」、「ピンク」は「真の異常」です。

サンプルのエッジの色はアルゴリズムが判定した結果を表しています。「緑のエッジ」は「正常と判定」、「赤のエッジ」は「異常と判定」の意味です。サンプルの位置が閾値より左側であればエッジは緑に、右側であればエッジは赤になります。

「正解の割合」は上の図でも示したようにTPRと呼び、以下のように定義できます。

TPR = 異常のサンプル（ピンク）のうち異常と正しく判定をした割合

TPRは「True Positive Rate」の略で、日本語では真陽性率となります。うーん、ややこしい名前ですよね。「陽性(Positive)」というのは、病気の検査などで使われる用語で、病気と判定されることが「陽性(Positive)」となります。この「陽性(Positive)」が異常検知でいう所の「異常」に対応します。

つまりTPRは、「正しく（True）異常（Positive）を検出できた割合（Rate）」という意味になります。異常検知アルゴリズムの性能は、TPRが大きいほどよいということになります。

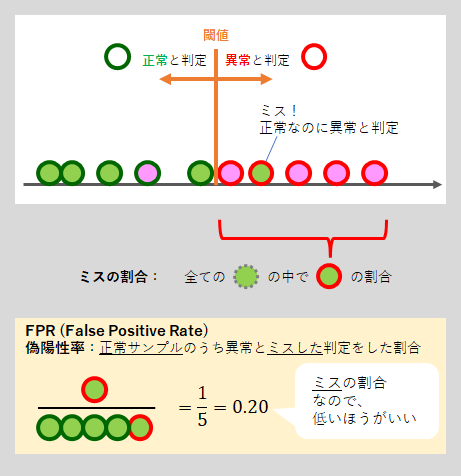
3. ミスの割合、False Positive Rate (FPR)

異常検知アルゴリズムは、異常を逃さないことも重要ですが、「正常なのに異常と判定してしまうミスの割合」はできるだけ小さくしなくてはいけません。これも、異常検知の重要な指標であり、以下の図のように考えます。

まとめると、「ミスの割合」は、

FPR = 正常のサンプル（黄緑）のうち異常とミスした判定をした割合

で定量化することができます。

FPRは、「False Positive Rate」の略で、日本語では偽陽性率となります。つまり、FPRは「間違って（Flase）異常（Positive）と検出してしまった割合（Rate）」ということになります。異常検知アルゴリズムの性能は、FPRが小さいほど小さいほどよいということになります。

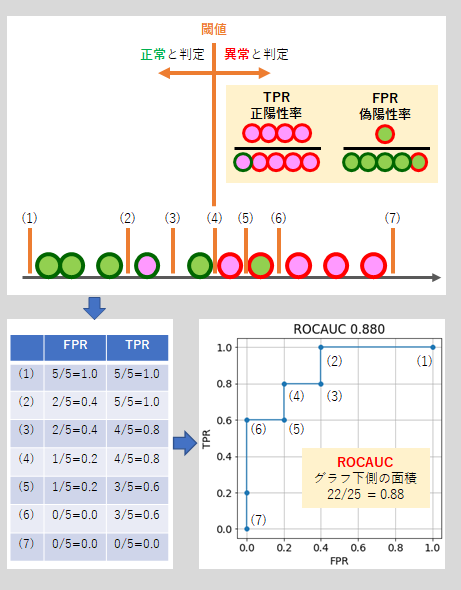
4. すべての閾値で評価、ROC曲線とROCAUC

TPRとFPRは閾値によって値が変わります。

TPRはできるだけ1に近い方がよいですが、TPRを1に近づくように閾値を動かすと、FPRも増えてしまうことが普通です。

この関係性が一目でわかるように、「すべての閾値に対して、TPRとFPRの組の値をグラフにプロット」したものが以下のROC曲線になります。以下の図のように、閾値を(1)から(7)まで変えたときのFPRとTPRを計算し、その値を座標としてプロットすれば、ROC曲線ができあがります。

そして、この「ROC曲線の下側の面積」をROCAUC (AUC; Area under the curve)と言い、これが異常検知アルゴリズムの性能の指標となります。

アルゴリズムの性能がよいほど、ROCAUCは大きい値となります。先に出した３つのアルゴリズムについてROC曲線を作成し、ROCAUCを計算したものを下の図でみてみましょう。

最高のアルゴリズムAのROC曲線は、左上のFPR=0、TPR=1 の点を通る線となり、ROCAUCは最高の1.00となります。一方、正常と異常のラベルが入り混じったアルゴリズムCのROCAUCは1.00よりも大分小さく、0.64という値です。

テストデータが十分にたくさんあれば、完全にランダムな値を出すアルゴリズムのROC曲線は、左下のFPR=0, TPR=0の点から、右上のFPR=1, TPR=1の点を結ぶ対角線となり、その時のROCAUCは0.5となります。

実際に計算してみると、ROCAUCが0.5よりも小さくなってしまった？！ということがあるかもしれませんが、この場合は、ラベルが逆になっていないか、プログラムにバグがないかなどを疑ったほうがよいでしょう。

以上が、ROCAUCの説明となります。このようにROCAUCは、閾値に関係しない指標になりますので便利ですね。

5. Python でROC曲線の描画とROCAUCの計算

Pythonでは、sklearnライブラリを使うと、ROC曲線の描画とAUCの計算は簡単にできます。

以下、google colaboratory を想定した実装です。

まず、グラフを描くためのmatplotlib.pyplotをインポートし、
ROC曲線とROCAUC用に、sklearn.metricsからroc_curveとroc_auc_scoreをインポートします。

cell1

import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score

データをリスト（numpy.arrayでも可）で準備します。

cell2

labels = [  0,   0,   0,   1,   0,   1,   0,   1,   1,   1]  # 0:正常, 1:異常
scores = [ 40,  60, 120, 170, 240, 280, 310, 360, 410, 460]  # 異常値

FPRとTPR、ROCAUCの値は以下のようにして取得できます。

cell3

fpr, tpr, th = roc_curve(labels, scores) # FPR, TPRの計算 (A)
rocauc = roc_auc_score(labels, scores)   # ROCAUCの計算 (B)

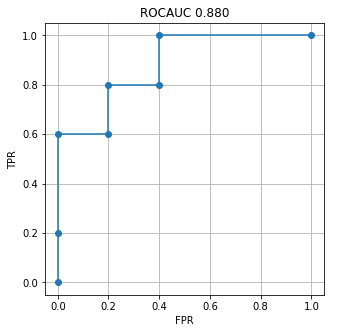
ROC曲線の描画は、普通にplt.plot()が使えます。

cell4

plt.figure(figsize=(5, 5))
plt.plot(fpr, tpr, '-o')
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.title(f'ROCAUC {rocauc:.3f}')
plt.grid()
plt.show()

cell4 の実行結果

6. さいごに

最後まで読んでいただきありがとうございます。
次は、このROCAUCを使って、ディープラーニングを使った異常検知を紹介していきたいと思います。
よろしくお願いしたします。

2021/8/18 K.T氏からROCAUCの最低値についてのコメントをいただき本文中に反映しました。ありがとうございました。またタイポの指摘もありがとうございました。