Go to Qiita Advent Calendar 2024 Top
LoginSignup
27
28

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@makotoito(makoto ito)

深層異常検知（１） Gaussian-AD; 学習時間ほぼなしの高性能異常検知アルゴリズム

Last updated at Posted at 2021-08-27

soap-bubbles-3540411_1280s.jpg

こんにちは。LiNKX株式会社のitoです。

ディープラーニングを使った異常検知を深層異常検知と言いますが、その中でも注目度が高い Gaussian-ADを紹介します。

Gaussian-ADは、ドイツのアーヘン工科大学のチームが2020年に紹介したアルゴリズムです1。普通のPCで軽々と動き、学習にかかる時間はほとんどありません（普通のPCで1分とか2分のレベル。対して、通常ディープラーニングで画像の学習をさせるとGPU付きの高性能PCでも数時間から数日かかったりします）。それなのに、精度は2020年の異常検知ベンチマーク(MTVec AD)でNo.1というすごいアルゴリズムです(PaperWithCode参照)。ちなみに、Gaussian-ADという名前は、このPaperWithCodeで使われているニックネームです（論文では特に名称の指定がありません）。

Gaussian-ADはQiitaのブログでもすでに紹介されており2 3、そのすごさが称えられています。

このブログでは、Gaussian-ADの概要とその動作を丁寧に解説し、さらに、あまり掘り下げられていないネットワークの構造についても補足Aで紹介します。

// 過去の異常検知ブログはこちら //
異常検知（１） 確率分布による基本の異常検知
異常検知（２）ガウス分布を仮定する異常検知、ホテリングのT2法
異常検知（３）データがガウス分布から外れていても使える、k近傍法
異常検知（４）時系列信号の変化の検知、特異スペクトル法など
異常検知アルゴリズムの評価方法 ROCAUC を分かりやすく説明
深層異常検知（１） [Gaussian-AD; 学習時間ほぼなしの高性能異常検知アルゴリズム] <--- このブログ

1. Gaussian-ADの概要

では、Gaussian-ADの仕組みについて簡単に説明します。

1-1. Gaussian-ADができること

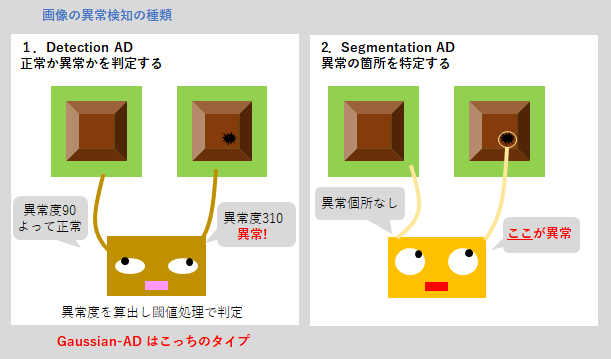
画像の異常検知(Anomaly Detection; AD)には、入力画像が正常か異常かを判定するDetection ADと、異常の場所を特定するSegmentation ADがあります。

image.png

ここで紹介するGaussian-ADは、前者の「Detection AD」用のアルゴリズムです。

Gaussian-ADは、通常の異常検知アルゴリズムと同様に、入力画像に対して異常度という数値を出力するので、異常と判定する閾値を設定して運用します。

1-2. Gaussian-ADの仕組み

Gaussian-ADは、学習が完了している自然画像の分類モデルを使います。補足Aで詳しく説明しますが、EfficientNetと呼ばれるGoogleが作った高性能分類モデルです。

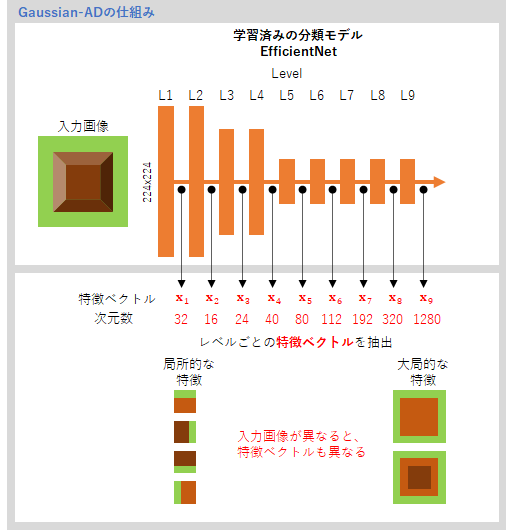
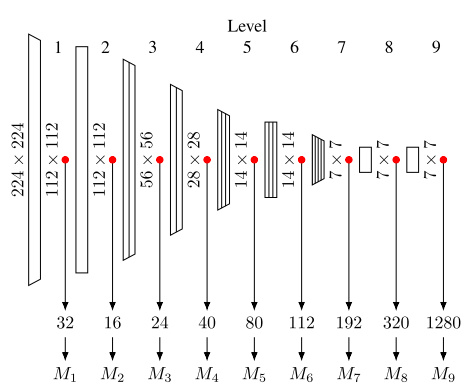
このEfficientNetは多層の畳み込みディープラーニングモデルですが、下の図のように、9つのレベル（ブロック）に分割することができます。レベルとは、EfficientNetで定義された情報処理の単位で、1つのレベルには同じ種類の層が複数層含まれます（補足A参照）。

image.png

EfficientNetに画像を入力すると、L1からL9へと情報処理が進みますが、この途中の情報を抜き出すのがGaussian-ADの特徴です。L1での情報処理結果を32次元のベクトル${\bf x}_1$として抜き出し、同様に、L2, L3, ..., L9 までの情報処理結果を16, 24, ..., 1280次元のベクトル ${\bf x}_2$, ${\bf x}_3$, ..., ${\bf x}_9$ として抜き出します。

一番初めの${\bf x}_1$ は画像の局所的な特徴をとらえた（局所的な特徴で変化しやすい）ベクトル表現であり、レベルが上がるほど、大局的な特徴をとらえた表現になっていると考えらえます。

このEfficientNetで特徴抽出した${\bf x}_L$ に対して基本の異常検知アルゴリズムであるホテリング$T^2$法を適用するのがGaussian-ADです。ホテリング$T^2$法については、「異常検知（２）」で説明していますので参考にしてください。

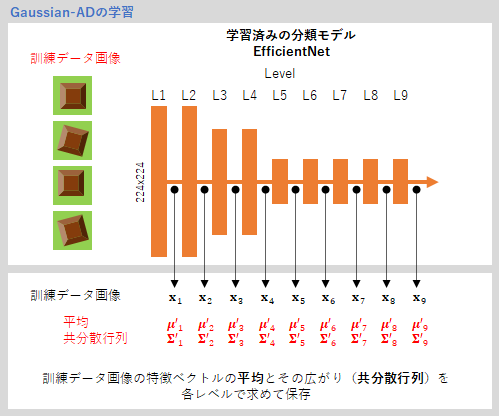
学習フェーズでは、複数の訓練データ画像（正常画像）をEfficientNetに入力し、各レベルでの特徴ベクトル${\bf x}_L$の平均$\boldsymbol{\mu}_L'$と共分散行列$\boldsymbol{\Sigma}_L'$を求めて保存します。学習フェーズといえども、学習済みのネットワークに画像を入れるだけで、ネットワークの重みを変えるという操作はありませんから、この計算にはほとんど時間はかかりません。これが、Gaussian-ADの学習が高速である秘訣です。

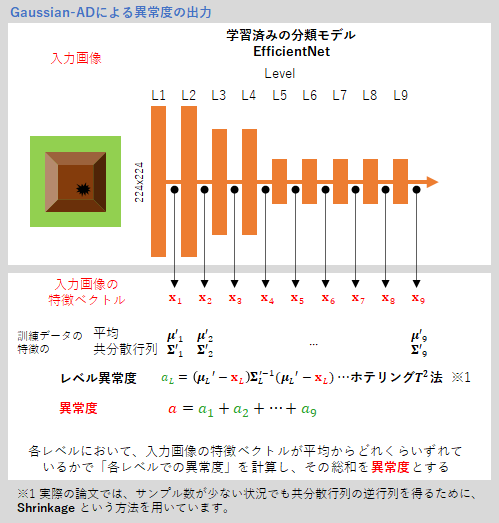
image.png

運用時には、入力画像に対する異常度を計算することが目的になります。

EfficientNetで入力画像の特徴ベクトル${\bf x}_L$を算出し、各レベルにおいて、${\bf x}_L$が平均からどれくらいずれているかで「各レベルでの異常度」を計算し （ホテリング$T^2$法）、各レベルでの異常度の総和を異常度とします。

これが、Gaussian-ADです。とてもシンプルです。

image.png

2. ベンチマークの画像での動作確認

それでは、まず、このアルゴリズムの評価に使われた異常検知ベンチマークのデータベース、MVTEC ADの画像での動作を確認しましょう。

2-1. データ

「MVTEC AD」は、2019年に公開された、15種類の工業用品や農作物からなるデータベースです。

image.png
図は 公式HPより転用（一段目が正常の画像、２段目が異常の画像、３段目が異常箇所の拡大）

この15項目の中で「カプセル」が見た目で分かりやすいので（上図左から３列目）、これを使うことにします。

各カテゴリーのデータは訓練データとテストデータに分かれています。

「カプセル」の「訓練データ」には、正常のみの画像（219枚）が含まれています。

「テストデータ」には、正常画像（23枚）といくつかの種類の異常画像（ひっかき傷 23枚、歪み20枚、印刷不良22枚、など）が含まれています。他にも異常画像はありますが、今回試すのはこの3種とします。まとめると下のようになります。

  • 訓練データ
    • 正常画像 --- 219枚
  • テストデータ
    • 正常画像 --- 23枚
    • 異常画像
      • ひっかき傷(scratch) --- 23枚
      • 歪み（squeeze) --- 20枚
      • 印刷不良(fauly_imprint) --- 22枚

訓練データ（正常画像）の例です。当然ですが、正常画像にもばらつきがあります。例えば、左側の黒いキャップ部分に白い文字が見えているものと見えていないものがあります。一方右側の「500」の文字は常に見えているように配置されています。

image.png

2-2. 学習

ではデータが準備できたので学習です。学習は、何を「正常」とするかを決めるフェーズと言えます。

学習は1-2で説明しましたように、各画像の特徴ベクトルを9つのレベルで抽出し、その平均と共分散行列を保存します。私の普通のノートPC（windows 10, CPU:i5-10210U, RAM:8M, GPUなし）で、219枚の訓練データの処理にかかった時間は、たった68秒でした。これで準備OKです。

実装は、下のgithubのコードをもとに、任意の画像が入力できるものを作りました。
https://github.com/byungjae89/MahalanobisAD-pytorch

著者らのオフィシャルのコードは以下で共有されています。
https://github.com/ORippler/gaussian-ad-mvtec

2-3. 動作テスト

では、テスト画像を入力して、異常度の数値を見てみましょう。

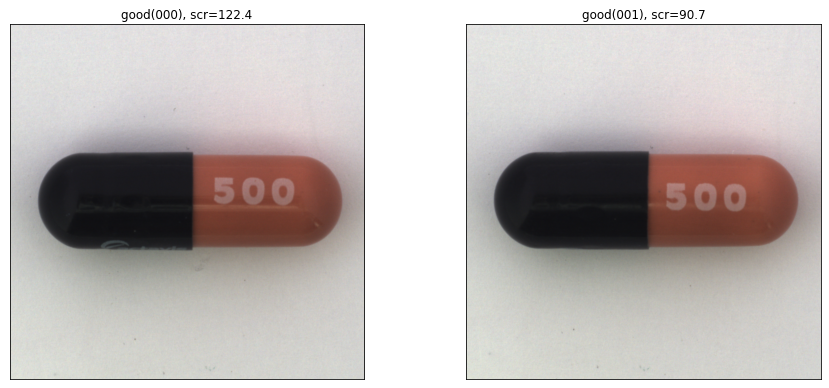
まずは、正常画像からです。
画像タイトルの「scr」がアルゴリズムが算出した異常度になります。左が122.4、右が90.7です。正常画像だと、異常度は100前後のようです。

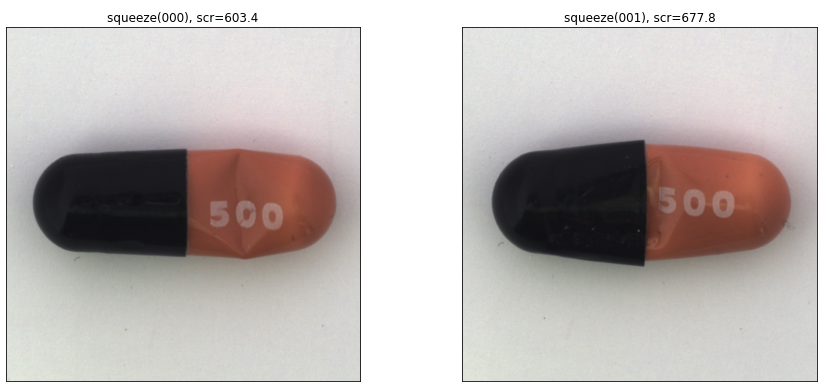
image.png

では、「歪みの異常画像」(squeeze)を入力します。

左は603.4、右は677.8です。正常画像に比べてずっと大きな異常度が出力されました。うまく動いているようですね。

image.png

次は、「ひっかき傷の異常画像」(scratch)です。歪みに比べて画像の差異はかなり小さいものになっています。

image.png

しかし、異常度は、172.8と152.5なので、最初の正常画像（122.4と 90.7）よりも、ちゃんと大きい数値が帰ってきています。

最後、「印刷不良の異常画像」(faulty imprint)です。

image.png

これも、数値は179.4と147.2なので、最初の正常画像（122.4と90.7）よりも、ちゃんと大きい数値となっていますね。ちなみに、印刷不良は「500」の文字に限った印刷不良ということのようです。

2-4 動作の評価

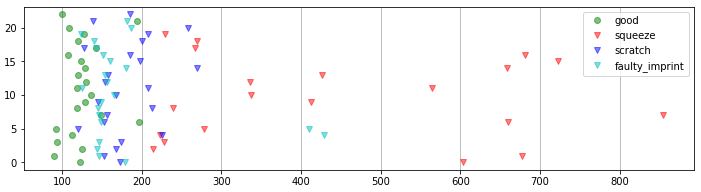
全てのテスト画像に対して異常度を計算しプロットしたものが下です。横軸が異常度、縦軸が画像番号です。

image.png

「good」（緑）が正常画像の異常度です。他の異常に対して小さい値をとっていることが分かります。

異常画像の方は、種類によって異常度の大きさがかなり異なっていました。「squeeze」（歪み；赤）は比較的大きい値をとっていますが、「faulty imprint」（印刷不良；水色）と「scratch」（ひっかき傷；赤）は低めで、正常画像の異常の分布と若干の重なりがあります。

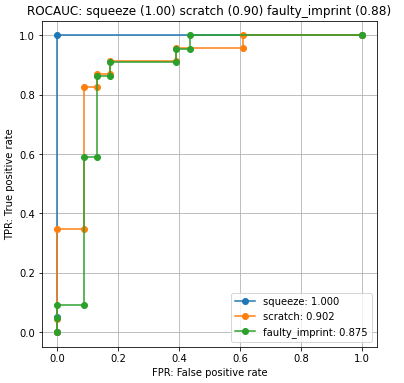
各クラスに対する異常度判別の精度は、ROC曲線を作成し、その下部面積であるROCAUCで定量化できます。ROCAUCは1に近いほど精度が高いという指標です。ROCAUCの説明は「異常検知アルゴリズムの評価方法 ROCAUC を分かりやすく説明」を参考にしてください。

image.png

「squeeze」（歪み）のROCAUCは1なので、テストデータでは完全に正常と異常を分けることができたということになります。
それに比べると、「scratch」（ひっかき傷）、「faulty imprint」（印刷不良）は、それぞれ、0.90と0.88なので、精度は若干低めですね。

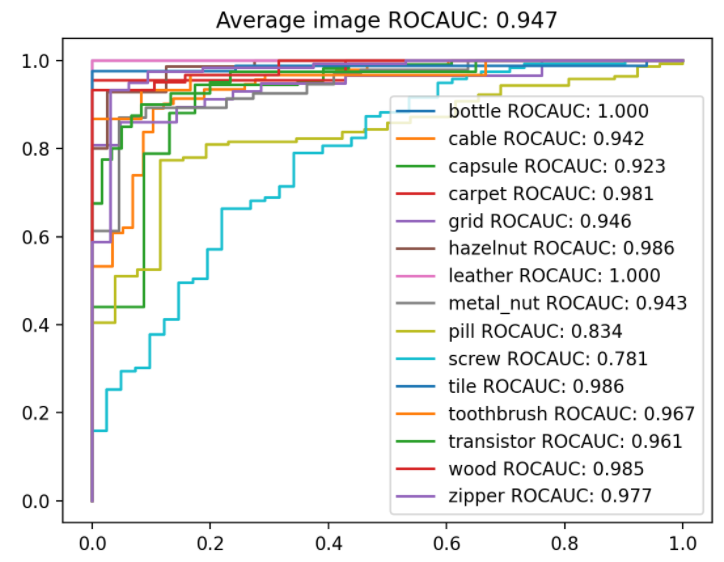
15種類すべてのカテゴリーに対するROCAUCを計算するPythonコードと結果が以下のgithubで参照できます。https://github.com/byungjae89/MahalanobisAD-pytorch

image.png

図はbyungjae89/MahalanobisAD-pytorchより転用

ROCAUCが高いのは、bottle(瓶；1.00)、leather（皮；1.00）、hazelnut（ヘーゼルナッツ; 0.986)、tile（タイル；0.986）、wood（木；0.985）、carpet（カーペット；0.981）です。
一方、ROCAUCが低いのは、screw（ネジ；0.781）、pill（ピル；0.834）です。

どうやら、皮、タイル、木、カーペットなどと、テクスチャー系は強いように見えますね。それだけではなさそうですが、得意不得意を分析すれば、良い運用ができそうです。

3. 自作100円玉画像での動作確認

Gaussian-AD、いい感じですね。それにしても、ベンチマークにない画像でもちゃんとうまくいくのでしょうか。そこで、100円玉を10枚集めて画像データを自作し、そのデータでの動作も見てみました。

3-1. 訓練データ

100円玉の表（桜側）の「日本国」の文字が上になるようにして、1つの100円玉で10枚撮影（各画像につき位置・角度をほんの少しだけ変化させる）し、これを10個の100円玉で行い、合計100枚作成しました。画像サイズは640x480ピクセルです。

image.png

3-2. 学習

上で準備した訓練データ100枚の学習にかかった時間は、たったの24.1秒でした。早い。

3-3. 動作テスト

では、いろいろなテスト画像に対して異常度（scr）を見てみましょう。

まずは、正常画像の異常度。もちろん訓練データにはない画像です。130～140くらいの値でした。

image.png

下の画像は、ゴミ（アルミホイル）が付着している異常の場合です。この3つの例では、異常度は全て300以上となっています。いい感じですね。

image.png

下のように、90度回転させた場合ではどうでしょうか。これも異常度は270以上となり、正常の範囲（130～140）より高い値となりました。

image.png

裏表が違っていたらどうなるでしょうか。どれくらいの異常度がでるのか見てみると、900以上というすごい高い数値となりました。

image.png

違うコインだったら？これも680以上というとても高い数値となりました。

image.png

とてもよいパフォーマンスだと思います。

3-4. 動作の評価

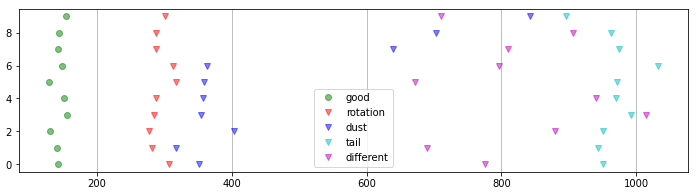
テストデータとして、正常画像10枚、すべての異常タイプに対して10枚の画像を作り、異常度をプロットしました。

image.png

「good」（正常画像）の異常度が150付近であるのに対して、「rotation」（90度回転）、「dust」（ゴミ付着）、「tail」（裏返し）、「different」（違うコイン）のすべての異常画像の異常度が250以上となりました。

正常画像と異常画像の異常度の分布に重なりがないので、（テストデータの範囲では）ミスなしで異常検知ができることを示しています。

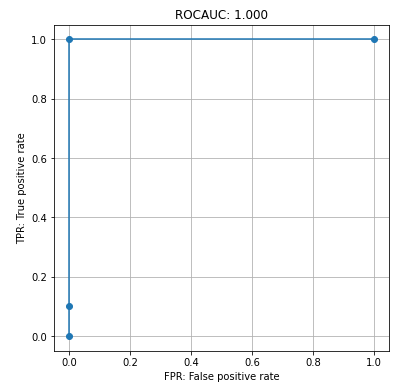
全テストデータでのROCAUCは最高点の1.00となりました。

image.png

たった30秒弱の学習時間でこれだけのパフォーマンスが出せるというのは素晴らしいと思います。

4. さいごに

Gaussian-AD、いいですね。いろいろと使い道がありそうです。

レベル毎に異常度を出してまとめるというアイディア、「なるほど！」と思いました。ただ、少し不思議に思ったのは、各レベルでの異常度を何の重みづけもせずにそのままの和を「異常度」としているところです。

論文では、「これでもいいパフォーマンスが出た」とのみあり、実際それでもよさそうなのですが、対象物が決まってしまえば、レベル毎に重みづけを入れるというチューニングで精度は上げられそうですね。

論文では1、さらにPCAと組み合わせるという方法も紹介しています。主要な主成分を捨てるとさらにパフォーマンスが上がるという結果は興味深いです。

最後に、あえてGaussian-ADでは難しい異常検知を2点考えてみたいと思います。

１．正常画像のバリエーションが大きいと大変になると考えられます。対象物自体が不定形である場合以外にも、外光が変化したり、対象物への光の当たり方が様々だったり、背景が一定でない場合などでバリエーションが大きくなるでしょう。

このような場合、訓練データにはそのバリエーションを十分にカバーする量のデータが必要になるでしょう。しかし、バリエーションをカバーできたとしても、その分布がガウス分布で近似しにくくなりパフォーマンスが落ちるという可能性も出てくるでしょう。

２．特定の部分のサイズや面積、角度などが閾値を超えたら異常とするような異常検知には向いていないでしょう。このように異常を数値で定義できる異常検知の場合は、従来のシンプルな画像処理による異常検知で実装する方がよいと思われます。

まとめると、Gaussian-ADは、「正常の製品はほぼ一定だが、異常のバリエーションが様々で数値化できないような場面で力を発揮するアルゴリズム」、と言えるのではないでしょうか。この特性にマッチするお題を見つけて実践で使ってみたいですね。

最後まで読んでいただきありがとうございました！

2021/8/26 TKo氏、YK氏から有用なコメントをいただき、内容を改善させることができました。ありがとうございました。

補足A Efficient Net

Gaussian-ADは、画像分類用のEfficientNetというgoogleが考案したディープラーニングモデルを使っています4 5。

EfficientNetは、画像分類のベンチマークデータベース、ImageNetにおける2019年のNo.1モデルです。

EfficientNetというのは、正確にはEfficientNet-B0から、EfficientNet-B7までの規模の異なるネットワークモデルの集合体を指します。B0が一番軽いベースのネットワークであり、ここから「解像度」「層」「チャンネル数」を一定の比率で増加させ、B1からB7までが提案されています。

B7が一番規模が大きく、精度も一番高いのですが、計算時間もかかります。動作環境に合わせて、適切な規模のEfficientNetを選ぶことが大切です。Gaussian-ADで使われているのはこのうちのEfficientNet-B4です。

ベースとなったEfficientNet-B0 は、Gaussian-ADのオリジナルの論文1では、以下の図で説明されています。

image.png

図は GaussianADのオリジナル論文（Ripple2020）4 から転用

ディープラーニングを知っている方用の説明になりますが、右端から224x224, 112x112, ... と続く数値は処理されていく画像のサイズです。徐々に小さくなって最後は7x7になります。その分、チャンネルという次元が増えていきますが(フィルターの数に対応します)、それが特徴ベクトル(32, ..., 1280 )の次元に対応しています。特徴ベクトルは、各チャンネルに対して画像を平均化したものとなっています。

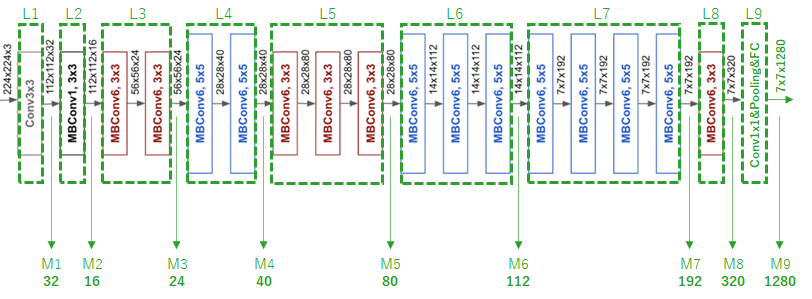
ただ、この図だけでは具体的な構造（各レベルの層数や層のタイプ）はよく分かりません。しかし、google AI blog 5 の方で、もう少し具体的な構造図が紹介されています。ただ、この図も最後の層が省略されていると思いますので、それを私が補足して、Level との対応を書き加えたのが下図になります（緑がitoが補足した部分です）。

image.png

図はGoogle AI Blog より転用修正5

ここで、はじめと最後の層で使われている「Conv」は通常の「Convolution layer」（畳み込み層）です。それ以外は、MBConv（mobile inverted bottleneck convolution）と呼ばれる層で構成されています。

MBConvはConvの計算量を少なくするために提案された近似手法だと思いますが、詳しくはMobileNetV2の論文を参照してください6（私もまだここは勉強中です）。

ところで、EfficientNet-B0のこの構造についてですが、これは、専門家がハンドチューニングで作ったものではありません。少ない計算量で、かつ、精度がでるように、自動探索でたどりついた着いた構造なのです7。この自動探索アルゴリズムには強化学習が使われています。うーん、何から何まですごいです。

  1. GaussianAD: Rippel O, et al.,(2020) Modeling the Distribution of Normal Data in Pre-Trained Deep Features for Anomaly Detection, arXiv. ↩ ↩2 ↩3

  2. @sUenaraE4 氏【異常検知】MVTec-ADを学習無しで正常/異常分類する ↩

  3. @shinmura0 氏【異常検知】学習ゼロの衝撃！を可視化する ↩

  4. EfficientNet: Tan M, et al., (2019) EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks, arXiv. ↩ ↩2

  5. EfficientNet: Tan M, (2019) Improving Accuracy and Efficiency through AutoML and Model Scaling, google AI blog. ↩ ↩2 ↩3

  6. MobileNetV2: Sandler M, et al., (2019) MobileNetV2: Inverted Residuals and Linear Bottlenecks, arXiv.](https://arxiv.org/abs/1801.04381) ↩

  7. MNasNet: Tan M, et al., (2019) MnasNet: Platform-Aware Neural Architecture Search for Mobile, arXiv. ↩

27
28
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
27
28

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?