異常検知（４）時系列信号の変化の検知、特異スペクトル変換法など

こんにちは。LiNKX株式会社のitoです。

このブログは、以下のシリーズの（４）となります。

• 異常検知（１） 確率分布による基本の異常検知
• 異常検知（２）ガウス分布を仮定する異常検知、ホテリングのT2法
• 異常検知（３）データがガウス分布から外れていても使える、k近傍法
• 異常検知（４）時系列信号の変化の検知、特異スペクトル法など <----- このブログ
• 異常検知アルゴリズムの評価方法 ROCAUC を分かりやすく説明
• 深層異常検知（１）Gaussian-AD; 学習時間ほぼなしの高性能異常検知アルゴリズム

※このブログは、会社の考え方ではなく私個人の解釈です。もし、私の思い込みで間違った解釈や記述がありましたら、ご指摘いただけると幸いです。

---

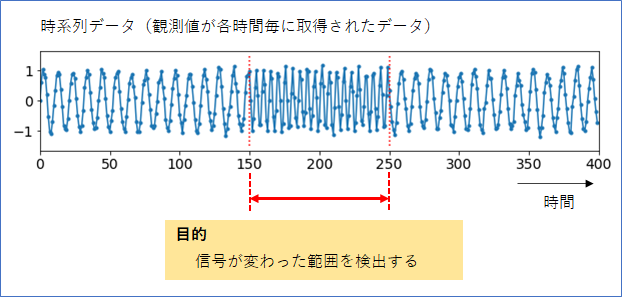
この異常検知（４）では、下図のような時系列信号の変化の検知（変化検知）を考えます。「データを複数点観測しないと異常が分からない」という点がこれまでとは異なるポイントです。時系列信号が「変化した区間」を検出したい場合と、「変化した時刻」を検出したい場合がありますが、本ブログでは前者を考えます（前者ができれば、後者も可能です）。

以降、大まかな流れとして、まず、異常検知（２）（３）で考えてきた「ホテリングの$T^2$法」と「k近傍法」を使って変化検知を試します。そしてより安定した変化検知ができる「特異スペクトル変換法」を紹介していきます。

1. 時系列情報をベクトルの集合に変換

検査の対象とする時系列情報を$s(t)$とします。$t$ は時間を表し、$0$から$1, 2, \cdots$ と整数値で増えていくとします。時間の単位は「ステップ」と呼ぶことにします。

ここで、「1つのデータ点だけでは異常の検出ができない」ことへの対策として、「複数のデータ点をまとめて新しい1つのデータ点とする」という方法を考えます。このようにデータ点を再定義すれば、1つのデータ点に複数の信号が含まれることになり、「1つのデータ点だけで異常の検出ができる」ようになります。そうすれば、異常検知（２）（３）で考えてきた「ホテリングの$T^2$法」や「k近傍法」を使うことができます。

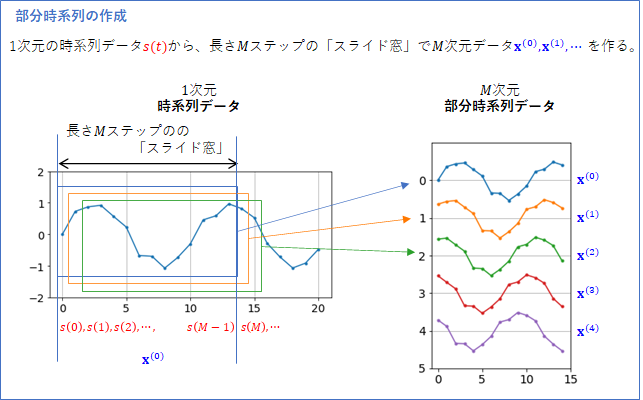
具体的に考えていきましょう。下の図のように、データの開始地点に長さ$M$ ステップの「スライド窓」（水色）を想定し、その範囲にある$s(0) \cdots s(M-1)$をまとめて、$M$次元のデータ点 ${\bf x}^{(0)}$ とします。

次に、スライド窓を右に1ステップずらし（オレンジ）、$s(1) \cdots s(M)$をまとめて、${\bf x}^{(1)}$を作ります。

この要領で、スライド窓を1ステップずらしながら、${\bf x}^{(t)}$を作っていきます。まとめると以下のようになります($T$ は縦ベクトルであることを表します)。

\begin{align}
{\bf x}^{(0)} &=& [s(0), s(1), \cdots, s(M-1)]^T \\
{\bf x}^{(1)} &=& [s(1), s(2), \cdots, s(M)  ]^T \\
{\bf x}^{(2)} &=& [s(2), s(3), \cdots, s(M+1)]^T \\
\vdots
\end{align}

このようにして作られた$M$次元のデータ点${\bf x}^{(t)}$ を、部分時系列と呼びます（参考文献[1]）。

2. 時系列情報の異常検知の問題の定義 I

ここで解くべく問題をクリアにし、最終的にどんなグラフを作ればよいかのイメージを作りたいと思います。

時系列信号$s(t)$から、長さ$M$ステップのスライド窓で、$M$次元の部分時系列データ${\bf x}^{(0)}, {\bf x}^{(1)}, \cdots $を作成したとします。

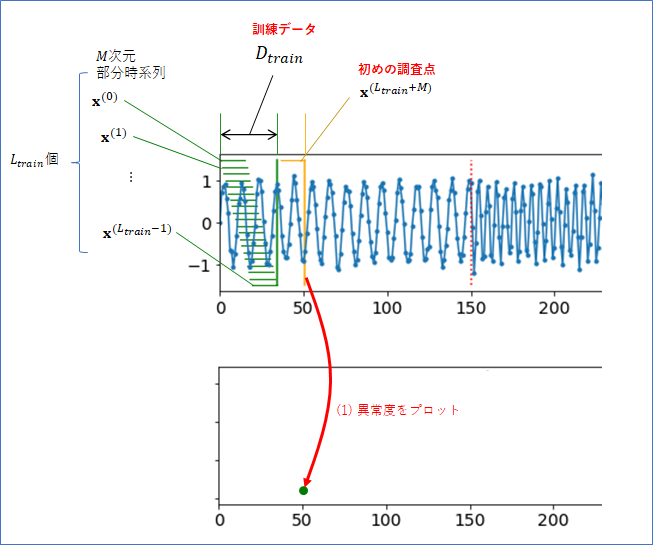
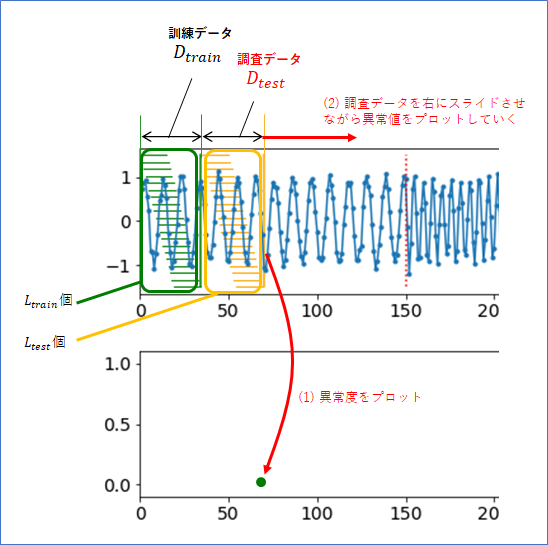
以下の図のように、最初の$L_{train}$ 個の ${\bf x}^{(0)}, \cdots, {\bf x}^{(L_{train}-1)}$ をまとめて訓練データ$D_{train}$とします¹。

そして、訓練データを含まないその他の部分時系列のデータ点を調査点²と呼ぶことにします。${\bf x}^{(L+M)}$ が初めの調査点となります。

ここで、時系列の異常検知の問題を、

「訓練データ$D_{train}$を使って、各調査点${\bf x}$に対する異常度$a({\bf x})$を求めなさい」

とします。

この問題は、異常検知（２）（３）で考えてきた「異常検知の問題設定」と本質的に同じです。部分時系列を定義したことで、「時系列の異常検知の問題」が、普通の「異常検知の問題」として扱うことができるようになったということです。

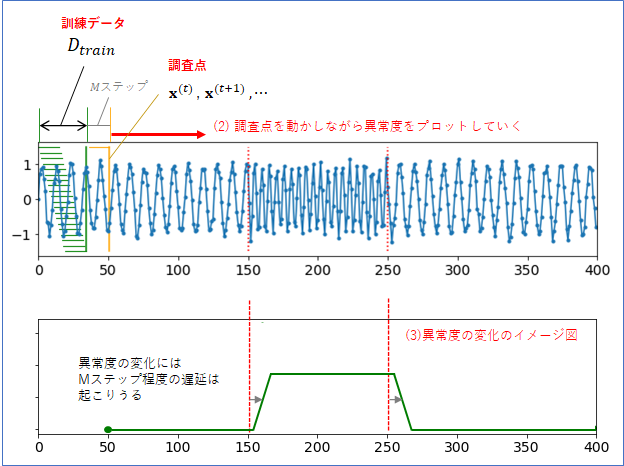
では、各調査点の下にその異常度をプロットすることを考えます。上図の(1)のイメージです。プロットする時間は、調査点が含む時系列情報の一番新しい（右端の）時間とします。そして、下図の(2)のように、調査点を右に動かしながら異常度をプロットしていくことを考えます。

(3)は異常度のグラフのイメージ図になります(パワポで描きました)。時系列が変化したところで異常度は増加しますが、調査点が含む時間情報に$M$ステップの幅があることに注意すると、その増加には幾分かのディレイが生じることは致し方ないといえます。「信号が変化したある程度の遅延後に異常値は上がり、信号が正常に戻ったあとは、いくらかの遅延後に異常値は下がる」、こういったグラフが描ければ、成功といえるでしょう。

3. ホテリングのT2法とk近傍法で変化検知

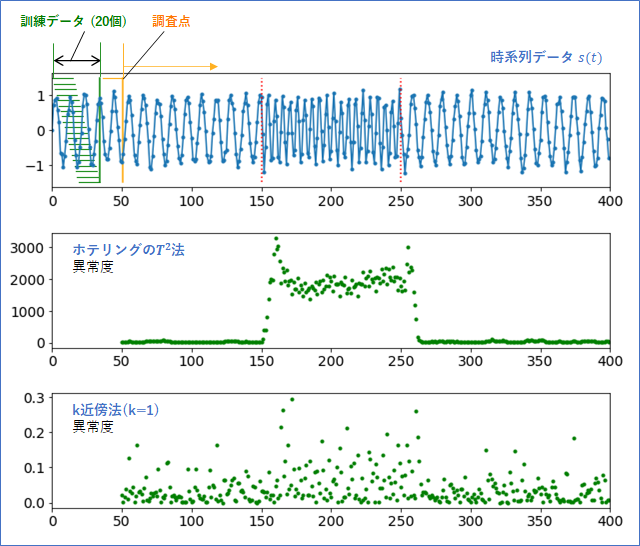
さっそく、この$M$次元の部分時系列データ${\bf x}^{(t)}$に対して、「ホテリングの$T^2$法」と「k近傍法」を試してみたのが下のグラフになります。スライド窓の長さは$M=15$、訓練データの数は$L_{train}=20$とした場合です。

意外にも、「ホテリングの$T^2$法」で異常度の検出がよかったです。遅延もほとんどなく、信号が変化した直後に異常度が反応していることが分かります。このようなサイン波から作った部分時系列は、実は高次元のガウス分布でフィッティングしやすい形に分布しているのだと思います。

一方、「k近傍法」の異常度はボロボロでした。これはk=1の場合の結果ですが、kを大きくしても結果は余計悪くなります。これは、k近傍法を使うにはデータが少なすぎるからだと思われます。データ次元が、15次元という高次元データなのに、データはたった20個だからです。この結果は、異常検知（３）で「k近傍法はデータが多くないとうまく動かない」と考察した通りでもあります。

4. 時系列情報の異常検知の問題の定義II

ここまでは、訓練データに対して、部分時系列の調査点1点から異常度を計算していましたが、調査点を複数まとめて調査データとし、「訓練データに対して、調査データの異常度を計算する」、という方法も考えることができます。調査点1点よりも複数点を含む調査データで異常度を計算する方が、よりノイズに強く安定すると期待できます。

そこで、以下のように、「問題の定義II」を考えます。

まず、時系列信号$s(t)$から、$M$次元の部分時系列データ${\bf x}^{(0)}, {\bf x}^{(1)}, \cdots $を作成したとします。

そして、以下の図のように、最初の$L_{train}$ 個の ${\bf x}^{(0)}, {\bf x}^{(1)}, \cdots, {\bf x}^{(L_{train}-1)}$ をまとめて訓練データ$D_{train}$とします。また、訓練データを含まない、連続した$L_{test}$ 個のデータを調査データ ³ $D_{test}$とします。

ここで、時系列の異常検知の問題を、

「訓練データ$D_{train}$を使って、各調査データ$D_{test}$ に対する異常度$a(D_{test})$ を求めなさい」

とします。「問題の定義I」と同様に、調査データの下に、異常度をプロットして結果とします。プロットする異常度の時間は、$a(D_{test})$が含む時系列情報で一番新しい（右端の）時間とします。

5. 特異スペクトル変換法の概要

「問題の定義II」を解く方法に、「特異スペクトル変換法」という方法があります（参考文献[1]）。この紹介がこの異常検知（４）のメインです。直感的に納得がいくように、行列中の数値データも波形データとして図示する説明を考えてみました。

5-1. 特異スペクトル変換法の適用例

特異スペクトル変換法は少し原理が複雑なので、まずは適用した結果から示したいと思います。

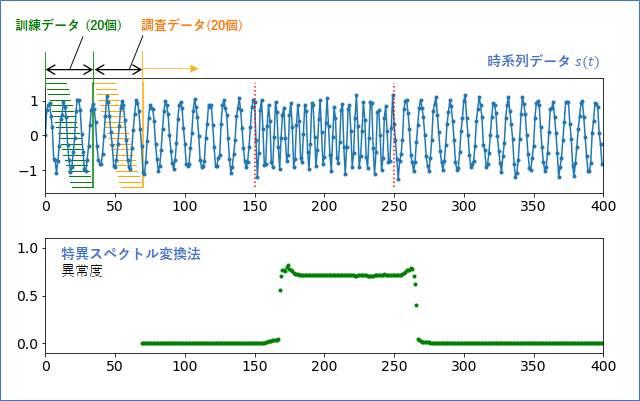
スライド窓の長さ$M=15$ 、訓練データ数 $L_{train}=20$、調査データ数 $L_{test}=20$ で行った結果です。信号が変化している区間で、想定していたディレイはありますが、異常度がきれいに立ち上がっていることが分かります。信号にはノイズが含まれていますが、異常度にはぶれがほとんどなく、安定した結果となっています。「調査点」で計算したホテリングの$T^2$法の結果よりも安定しています。

5-2. 要素波形を取り出す

それでは、「特異スペクトル変換法」の原理の説明です。この節「要素波形を取り出す」と、次の節「要素波形の違いを定量化する」の２段階で説明します。

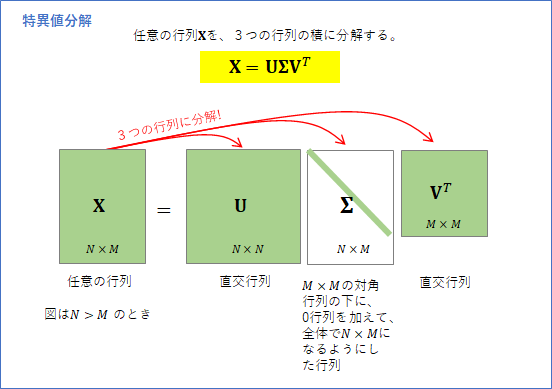
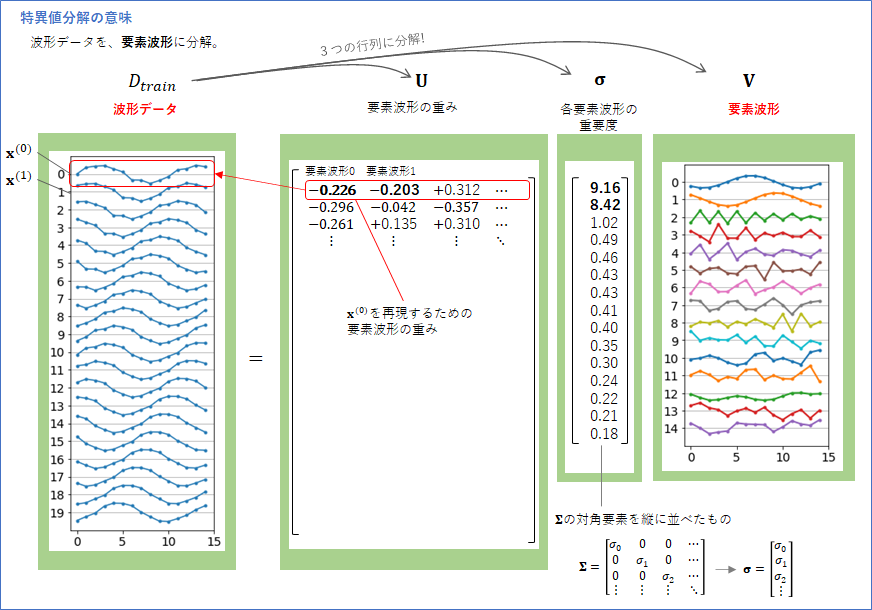
まず、「特異スペクトル変換法」は、特異値分解 という方法で時系列データの「要素」を取り出します。ここではこの要素に要素波形⁴という名前を付けました。「特異値分解」は、一般的には、以下の図に示したように、$N \times M$の任意の行列${\bf X}$を、3つの行列${\bf U}, \boldsymbol{\Sigma}, {\bf V}$に分解する方法です。

この特異値分解を訓練データ$D_{train}$に適用した場合を考えます。

$D_{train}$を、行ごとに部分時系列データが入った$L_{train} \times M$ の行列と考え、特異値分解を施して3つの行列に分解すると以下のようになります。図は$L_{train}=20$、$M=15$ の場合です。

ポイントは、一番右側の行列${\bf V}$です。行列${\bf V}$は、$M \times M$ の行列で、各列が「波形」を表します。図は$M=15$の場合なので、0から14までの合計15個の波形が表されています。この波形は、データの波形が、先ほど紹介した「要素波形」です。主成分分析をご存じの方は、それとの関係が気になるかもしれません。実は、波形データを主成分分析したときの主成分ベクトルが波形要素に対応します（特異値分解と主成分分析の関係については、 「PCAとSVDの関連について」が参考になります）。

ちなみに、$D_{train}$の定義を変えて、列ごとに部分時系列データを入れた$M \times L_{train}$ 行列で定義すると（転置の関係です）、UとVの役割が逆転します。参考文献[1]ではこちらで定義していましたが、ここでは、機械学習の流儀を採用して、$L_{train} \times M$ 行列で定義しています。

なぜこの${\bf V}$が「要素的な波形」と言えるかというと、${\bf X}$にある全ての波形データは、この「要素波形」に適当に重みづけした足し算で、再現することができるからです。

そして、$M$個の「要素波形」はすべて同等というわけでははなく、それぞれに重要度があります。それが$\boldsymbol{\sigma}$ で表された数値です。$\boldsymbol{\sigma}$ は、特異値分解で分解される対角行列$\boldsymbol{\Sigma}$ の対角成分に対応ます（特異値分解では特異値と呼ばれていますが、このブログでは意味が分かりやすいように「重要度」と呼ぶことにします）。

「重要度」が大きい要素波形は「波形データ」の再現に必須ですが、「重要度」が小さい要素波形は、なくてもあまり問題にならない（重要度が小さい波形を使わずに再現しても再現誤差は少ない）、ということになります。上の例での重要な要素波形は、「重要度9.16の要素波形0」と「重要度8.42の要素波形1」の2つだといえるでしょう。要素波形2からは重要度が1.02と極端に小さくなります。

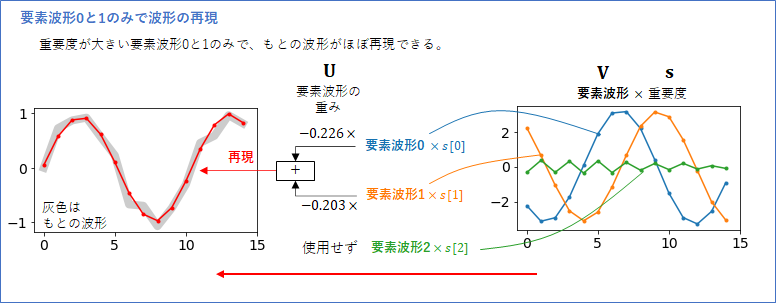
では、要素波形0と、要素波形1で、初めの波形データ${\bf x}^{(0)}$ を再現してみましょう。

まず、「要素波形」に「重要度」を掛け算した波形を考えます。下図の右側には、要素波形0、要素波形1、要素波形2 に重要度を掛け算した波形を示しています。要素波形2は、比較のために表示しましたが、重要度が低いので波形の振幅が大きくありません。

行列${\bf U}$ の0行目は、$[-0.226, -0.203, \cdots]$でしたが、これが0番目の波形データを再現する、要素波形の「重み」です（この「重み」の値は、これをベクトルとみなしたときに長さが1となるように正規化されています）。　

この「重み」と対応する（要素波形×重要度）に掛け算して、足し合わせたものが、上図左（赤線）になります。もとの波形データ（灰色）に、ほぼぴったり重なっていることが分かります。むしろ、元の波形のノイズ部分が除去されて再現されている、とも見て取れます。

このようにして、すべての波形データは、「重み」を変えることで、重要度の大きい要素波形から再現することができるのです。

ここで抽出された2つの要素波形は、「90度位相がずれた2つのサイン波」のような形をしています。サイン波は山から次の山までを360度の位相というので、90度はその1/4のずれになります。なぜ、サイン波が要素波形で出てきたかというと、もともとの波形データ（人工データです）は、サイン波にノイズを足して作られたものだったからです。

波形データはサイン波を1ステップずつずらした波形の集合ですが、この要素波形のような「90度位相の異なる2つのサイン波」があれば、重みをうまく調節ることで、「さまざまなステップずれ」のサイン波を再現することができるのです。

ここで、改めて、「重要度の高い要素波形とは」何か？を考えると、

重要度の高い要素波形とは、波形データの本質をコンパクトに表したもの

と言えると思います。

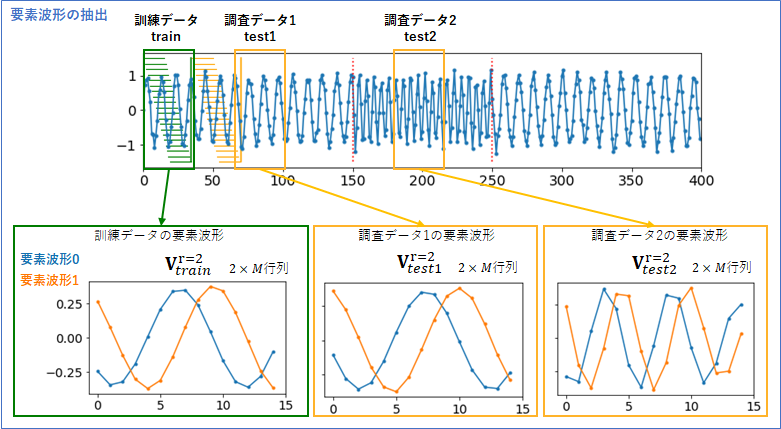
以上のような特異値分解を、「訓練データ」だけではなく、特定の「調査データ1」と「調査データ2」に対して行い、重要度の高い要素波形を抜き出した結果が下図です。

「調査データ1」は、訓練データと同様な波形を含んでいるので、要素波形は「訓練データ」のものと似ています。しかしよく見ると、「訓練データ」の要素波形に比べて、1ステップ分右に平行移動した波形となっています。サイン波を再現するための要素波形には、このような平行移動（位相）の自由度があり、その時のノイズの具合によって、任意の位相でのサイン波が要素波形として出現しますが、2つの要素波形の位相差は常に90度になります。

一方、「調査データ2」は、信号が変化している区間なので、要素波形も「訓練データ」のものとは異なっています。より周期の短い、位相が90度ずれたサイン波が抽出されています。

これで、「重要度の高い要素波形は、波形データをコンパクトに表したもの」という主張に納得がいったのではないかと思います。

よって、「訓練データと調査データの要素波形の違いを定量化」できれば、それを「異常度」として解釈できそうです。

5-3. 要素波形の違いを定量化する

では、「訓練データと調査データの要素波形の違いを定量化する」ことについて考えます。

その前に、1つ、注意しないといけないことがあります。前節で、訓練データと調査データ1から抽出した「要素波形」は似ていながらも、1ステップ分ずれているという違いがありました。ですので、要素波形間の違いを、例えば二乗誤差、で測るような方法ではうまくいきません。

「要素波形」そのものを比較するのではなく、「要素波形の和で作り出すことができる波形」の類似度を測る方法が必要です。そのような類似度を波形類似度⁵と呼ぶことにします。

結論から言うと、まさにそういった計算が行列ノルムを使うとできます。

「ベクトル」のノルムといえばベクトルの「長さ」を表しますが(p=2の場合)、それを行列に拡張したものが、「行列ノルム」ということです。あまり、なじみがないという方もいると思いますが、ここでは「波形類似度を計算するツール」として認めてしまうことにします。

行列ノルムの計算方法やその性質を詳しく知りたいという方は、「行列のpノルムの定義と性質」 がおすすめです。

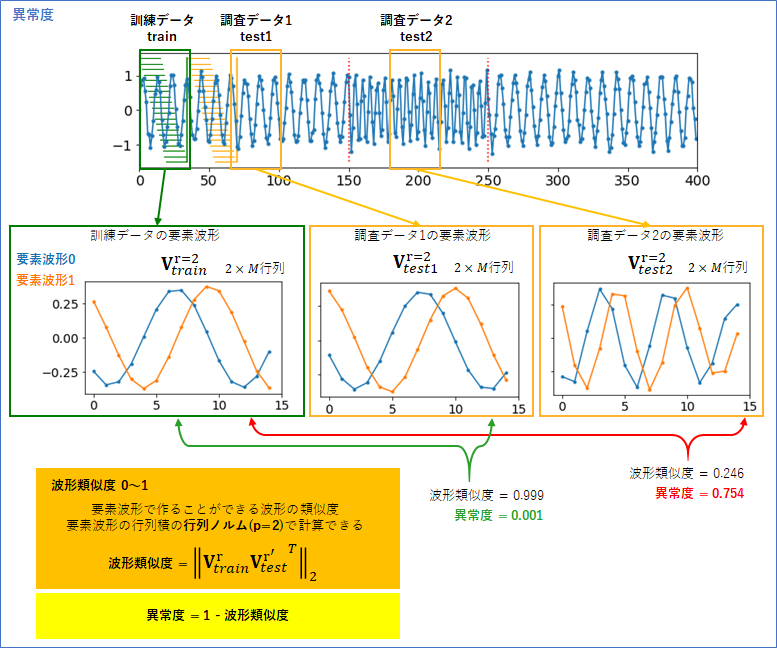
具体的には、訓練データの要素波形行列${\bf V}_{train}$の重要度の高い$r$ 個(今は2個)の要素波形を残した$r \times M$ の行列を以下のように表します。

{\bf V}_{train}^r

同様に、調査データの要素波形行列${\bf V}_{test}$の重要度の高い$r'$ 個(今は2個)の要素波形を残した$r' \times M$ の行列を以下のように表します。

{\bf V}_{test}^{r'}

この2つの行列の積の「行列ノルム」が、「訓練データと調査データの波形類似度」となります。

訓練データと調査データの波形類似度 = || {\bf V}_{train}^r {{\bf V}_{test}^{r'}}^T ||_2

$||\cdot ||_2$が行列ノルムの演算を表します。

具体的に、訓練データと調査データ1, 2の波形類似度を計算したものが下図です。訓練データと調査データ1は、波形類似度が0.999で、訓練データと調査データ2は、0.246でした。

ここまで計算できれば、異常度を作ることは簡単です。波形類似度は最高で1なので、異常度は、

異常度 = 1 - 波形類似度

と定義すれば、波形が異なっている時に異常度が高くなります。この定義で、訓練データと調査データ1の異常度は0.001で、訓練データと調査データ2の異常度は0.754となりました。もっともらしい結果がえられたと思います。

説明が長くなりましたが、このような流れで異常度を求める方法が、「特異スペクトル変換法」でした。

6. 特異スペクトル変換法の実装

特異スペクトル変換法のpythonによる実装として、以下の関数 sst() を紹介します。方法の説明は長くなってしまいましたが、整理すると計算すべきことは特に多くなく、コードはたった5行ですみます。　

import numpy as np 

def sst(X_test, X_train, r_test=2, r_train=2):
  U_test, sv_test, V_test = np.linalg.svd(X_test)      # 特異値分解 (A)
  U_train, sv_train, V_train = np.linalg.svd(X_train)  # 特異値分解 (B)
  C = V_train[:r_train, :] @ V_test[:r_test, :].T      # 行列の積 (C)
  normC = np.linalg.norm(C, ord=2)  # 行列ノルム (D)
  return 1-normC  # 異常度 (E)

引数のX_testは、これまで議論してきた、調査データ$D_{test}$を $L_{test} \times M$ の行列で表したものです。同様に、引数のX_trainは、$D_{train}$を訓練データ $L_{train} \times M$ の行列で表したものです。

r_testとr_trainは、それぞれ、調査データと訓練データに対して、何個の要素波形を重要として抜き出すかを調節するパラメータです。

sst()のコードの方に移りますと、まず、(A)と(B)が特異値分解です。numpy.linalg パッケージのsvd()で実行できます。(C)が行列の積であり、その行列ノルムを計算しているのが(D)になります。ord=2 は行列ノルムのp値を表しています。

ここでは、r_testとr_trainを手動で与えるようにしていますが、重要度を表すsv_testとsv_trainから自動でr_testとr_trainを決めるようにすると、実用的になるかなと思います。

8. さいごに

さて、ここまでの異常検知（１）（２）（３）では、「異常検知とはデータ分布$p({\bf x})$を知ることなり」と豪語してきたのですが、「特異スペクトル変換法」の背後にある確率分布は一体なんだったのでしょうか。

ここも興味深いところなのですが、今回に関しては、まだまとめるには私の考察が及ばないところもあり宿題にさせていただこうと思います。「$D_{train}$と$D_{test}$ のデータを2つのガウス分布で近似し、その分布の差をKL距離カルバック・ライブラー・ダイバージェンスで定量化したものが、、」などとまとめられればエレガントだったのですが、そうもいかないようです。

これで予定していた異常検知のシリーズは終わりです。読んでいただいた方、大変ありがとうございました。

それにしても、異常検知はまだまだ奥が深いです。ディープラーニングなどを応用した異常検知の技術もあります。また機会がありましたらまとめていきたいと思います。

2021/07/21 C.S氏には、分かりにくかった箇所の言い回しの案をいただきました。N.Y氏からはData行列の定義の仕方でUとVの役割が逆転することを指摘してもらい、その内容を加えました。K.T氏からは言葉やグラフの整合性に関する多くのコメントをもらい、だいぶブラッシュアップできました。ありがとうございました。

参考文献

[1] 井出・杉山著「異常検知と変化検知」機械学習プロフェッショナルシリーズ（講談社）
[2] PCAとSVDの関連について
[3] 行列のpノルムの定義と性質

1. ここでの「訓練データ」とは、これまで異常検知（２）（３）で考えてきた正常値データ$D$と同じものと考えてください（本ブログでは、以降の調査データと対比させるために、訓練データと呼ぶことにしました）。参考文献で紹介している履歴行列と似ていますが、ここでは、「時間でスライドさせない固定データ」として考えたいので、別な名前を付けました。 ↩

2. 異常検知（１）（２）（３）までは、「新しい観測」という呼び方をしていましたが、後半出ててくる「新しい観測の集合」とすっきりと区別するために、「調査点」「調査データ」という言葉を用いました。このブログ独自での呼び方となります。 ↩

3. 先に命名した「調査点」に対して、調査点のグループを「調査データ」と命名しました。このブログ独自での呼び方となります。 ↩

4. 意味が分かりやすいようにこのブログで付けた呼び方です。 ↩

5. 意味が分かりやすいようにこのブログで付けた呼び方です。 ↩