こんにちは。LiNKX株式会社のitoです。
このブログは、以下のシリーズの(3)となります。
- 異常検知(1) 確率分布による基本の異常検知
- 異常検知(2)ガウス分布を仮定する異常検知、ホテリングのT2法
- 異常検知(3)データがガウス分布から外れていても使える、k近傍法 <----- このブログ
- 異常検知(4)時系列信号の変化の検知、特異スペクトル変換法など
- 異常検知アルゴリズムの評価方法 ROCAUC を分かりやすく説明
- 深層異常検知(1)Gaussian-AD; 学習時間ほぼなしの高性能異常検知アルゴリズム
※このブログは、会社の考え方ではなく私個人の解釈です。もし、私の思い込みで間違った解釈や記述がありましたら、ご指摘いただけると幸いです。
異常検知(1)(2)までの要点をまとめますと、
「観測値の分布$p({\bf x})$を、$p'({\bf x})$で近似できれば、異常度は$a({\bf x}) = −\log p'({\bf x})$で表せます」
という内容でした。
異常検知(2)では、「ガウス分布」でデータを近似する「ホテリングの$T^2$法」を紹介しました。
今回のブログ、異常検知(3)は、データがガウス分布から外れている場合でも対応できる「k近傍法」を紹介します。
今回は、異常検知(2)の時とは異なり、直接異常度$a({\bf x})$を作ります。その後で、その異常度$a({\bf x})$に対応する確率分布$p'({\bf x})$を考察したいと思います。
以降、以下の流れで進めていきます。
1. 異常検知の問題の定義
ここは前回の異常検知(2)と同じ内容になります。
使用する変数と異常検知の問題を定義します。
まず、D次元の観測データを考えます。1回の観測データを以下の縦ベクトルで表します。インデックスはプログラムと合わせるために、0から始まりとします。
{\bf x} =
\begin{bmatrix}
x_0 \\
x_1 \\
\vdots \\
x_{D-1}
\end{bmatrix}
正常値として観察されたこのような観測データが$N$個あるとし、右肩のカッコの数字でデータのインデックスを表すことにします。それをまとめて $D$ とします。
D = \{ {\bf x}^{(0)}, {\bf x}^{(1)}, \cdots, {\bf x}^{(n)}, \cdots, {\bf x}^{(N-1)} \}
ここで、異常検知の問題を、
「この正常値の観測データ $D$ を使って、新しい観測${\bf x}$ に対する異常度 $a({\bf x})$を求める式を作りなさい。」
とします。異常度が分かれば、閾値を設定して、異常度がその閾値を超えたときに「異常」という警告を出すことができます。
2. ガウス分布から外れたデータとホテリングのT2法
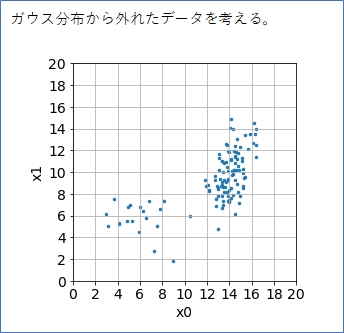
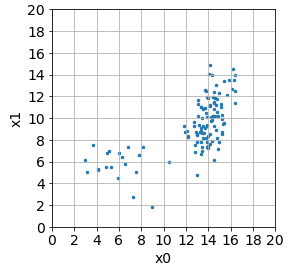
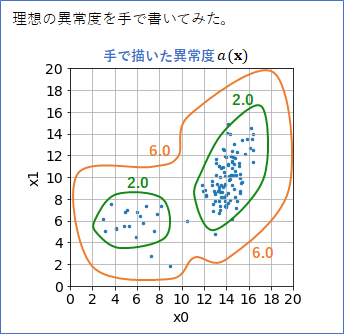
以下のように、観測するデータがガウス分布から明らかに外れているような場合を考えます。データはすべて正常値として考えます。
メインのデータの分布が右側にありますが、左下にも少数派の分布があることに注目してください。
このデータの分布対して、理想の異常度のイメージを手(パワポ)で描いてみたのが下です。2か所の分布に対して異常度が低くなって、そこから外れるほど異常度が高くなる、というところがポイントです。数値は適当です。
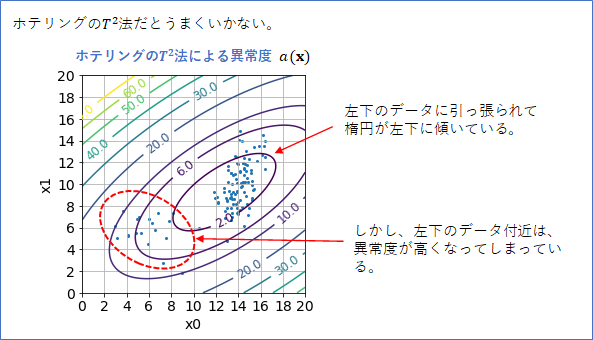
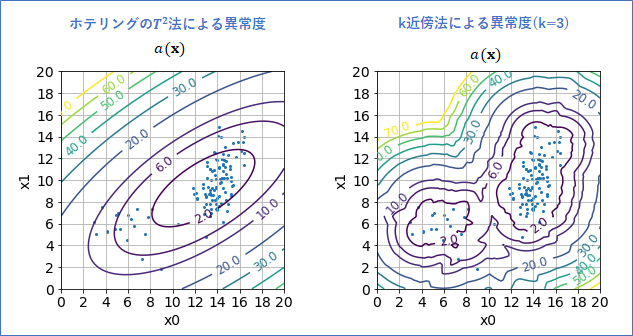
このデータ分布に対して、異常検知(2)で紹介したホテリングの$T^2$法を適用して異常度$a({\bf x})$を作ってみたら、案の定うまくいきませんでした。ホテリングの$T^2$法は1つのガウス分布をデータにフィッティングするのでこうなってしまうのはしょうがありません。
そこで、k近傍法の出番です。
3. k近傍法
k近傍法は、クラス分類の方法として有名ですが(wikipedia)、異常検知でも使われます(参考文献 [1])。
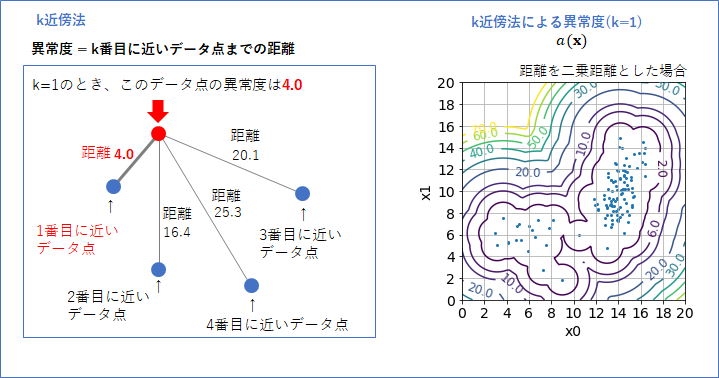
正常データしかない場合での k近傍法はいたってシンプルで、異常度は「k番目に近いデータ点までの距離」で定義されます。
k=1の時では異常度は、下の図のように、「異常度を測定したいデータ点から一番近いデータまでの距離」となります。新しいデータが、これまでのデータのどれよりも異なっていれば(距離が遠ければ)異常度は高くなるよね、ってことです。
これをx0-x1平面のすべての点に対して異常度を計算し、等高線表示したものが右図です。この等高線は距離に「二乗距離」を使って書きました(次に説明します)。いい感じの等高線が引けていると思います。
ここで「距離」をどう決めるかには選択肢があるのですが、ここでは通常の距離(ユークリッド距離)を二乗した「二乗距離」を想定して話を進めます。
観測${\bf x}=(x_0, x_1)^T$からデータ${\bf x}^{(n)}=(x_0^{(n)}, x_1^{(n)})^T$までの距離を$d_n$とすると、二乗距離は以下のようになります。
d_n({\bf x}) = (x_0^{(n)} - x_0)^2 + (x_1^{(n)} - x_1)^2
これを使って、異常度$a({\bf x})$は以下のように定義できます(上の言葉を式で表現しただけです)。
a({\bf x}) = \min_n d_n({\bf x})
異常度に「普通の距離」と「二乗距離」のどちらを使っても、閾値を調節すれば同じ異常と正常の境界線が引けますが、二乗距離の方が計算が楽です。最後にルートをとらないで済みますので。また、最後に確率分布を考える際に、二乗距離だと説明しやすいということもあります。
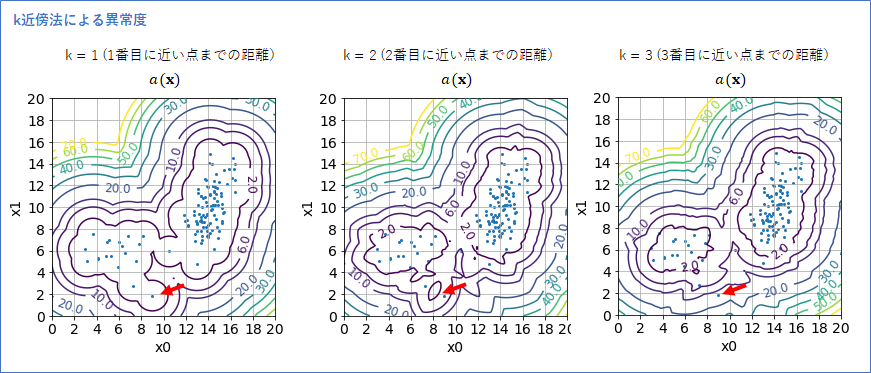
さて次に、kの違いで、異常度がどう変わるかを確かめようと、k=1, 2, 3 の場合の異常度の等高線を描いてみました。
k=1のときは、外れ値のように1つのデータがぽつんと存在する場合でも(上図 赤い矢印)、その点での異常度が小さくなったのですが、k=3になると、そのように1つのデータに異常度が引きずられるということがなくなり、境界線がより妥当な形になりました。
k=3のときのk近傍法の異常度は、初めに想像した理想の異常度に近く、メインの分布と左下の分布で異常度が小さくなっていることが分かります。
ホテリングの$T^2$法とk近傍法の異常度を並べてみました(下図)。この例だと、間違いなくk近傍法の異常度の方がよいですね!
それにしても、この結果を見てしまうと、「もう初めからk近傍法でいいじゃん、ホテリングの$T^2$法いらないじゃん」、と思ってしまうかもしれません。
そこで、ホテリングの$T^2$法と比べた場合のk近傍法のディスアドバンテージをあえて4つ考えてみました。
(1) kを自分で決めなくてはいけない。
(2) データの各次元に対するスケールを調節しなくてはいけない。
(3) データが多く必要。
(4) 新しい観測に対する異常度の計算がk近傍法は、データ数が多いほど多くなってしまう。
(1) kは設計者が自分で決めなくてはならないハイパーパラメータです。使えるデータ数によっても最適なkは変わります。ちゃんと決めるには、例えば、「$a({\bf x})$を作るときに使用しなかった新たなデータ(テストデータ:異常データと正常データ)を準備し、テストデータでの正答率が最も高くなるkを選ぶ」、というような方法が必要です。ホテリングの$T^2$法にはハイパーパラメータはありません。
(2) 例えば、長い釘の異常検知を考えます。横(頭の幅)の長さは平均10mm、 縦の長さは平均100mm の長い釘だとします。データは、横の長さを$x_0$mmとし、ネジの縦の長さ$x_1$mmとした2次元データ ${\bf x}=(x_0, x_1)^T$ とします。
このデータに対して、今のk近傍法を使うと、ネジの横の長さが1mmずれても、ネジの縦の長さが1mmずれても異常度は同じになります。しかしこれは変な感じです。ネジの横の方が短いので、ずれが同じでも横の同じずれに対しては異常度はより大きくなってほしいです。なので、例えば、ネジの横と縦の長さのずれが同等になるように数値を変換しておく前処理が必要になります。ホテリングの$T^2$ではある意味そのような差が自動的に調整されます(共分散パラメータの推定がその操作に値対応します)。
(3) k近傍法はある程度のデータの量が必要です。k近傍法の原理からして、データがスカスカだと、k近傍法の性能は著しく悪くなります。データの次元が多くなると、そのデータの空間をデータが埋め尽くすには大量のデータが必要になってきます。単純計算で、1次元分を10個のデータでカバーするとしたら、2次元では100個、3次元では1000個と次元に対して指数関数的に増えていきます。よって、データが少ない場合には、ホテリングの$T^2$の方が精度が出る可能性があります。
(4) 新しい観測データに対して異常度を計算するとき、k近傍法はそのたびに全てのデータ点までの距離を計算し、その距離を小さい順番に並べ替えるという処理が必要になります。すなわちデータが多ければ多いほど、計算に時間がかかってしまうのです。一方、ホテリングの$T^2$法は、手持ちのデータの平均値と共分散行列を1回作ってしまったら、新しい観測データに対する計算はデータ数には依存しなく一瞬で終わります(データ次元数 << データ数と仮定した場合)。
結局のところ、データの量や性質に合わせて、ホテリングの$T^2$法、k近傍法、またはそれ以外のアルゴリズムを使い分けることが大切ということですね。
4. k近傍法の実装
では、Pythonでk近傍法の関数を作ってみたいと思います。
google colaboratory を想定した実装です。
まず、numpyとmatplotlibをインポートし、表示の設定をします。
import numpy as np # ベクトル・行列計算ライブラリ
import matplotlib.pyplot as plt # グラフ表示ライブラリ
np.set_printoptions(precision=3) # 小数点以下の表示桁数
plt.rcParams["font.size"] = 14 # グラフのメモリのフォントサイズ
2次元の疑似データ120個を作成し (100x2)行列 xsとします。
np.random.seed(0)
mean = np.array([14, 10])
cov = np.array([[1, 1],[1, 4]])
mean2 = np.array([6, 6])
cov2 = np.array([[4, 0],[0, 4]])
xs = np.random.multivariate_normal(mean, cov, size=100)
xs2 = np.random.multivariate_normal(mean2, cov2, size=20)
xs = np.r_[xs, xs2]
def show_setting():
plt.figure(figsize=(4, 4))
plt.xticks(range(0, 21, 2))
plt.yticks(range(0, 21, 2))
plt.xlim([0, 20])
plt.ylim([0, 20])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid(True)
show_setting()
plt.scatter(xs[:,0], xs[:,1], s=6)
plt.show()
k近傍法での異常度を返す関数 knn() は、例えば、以下のコードで実装できます。
def knn(x, xs_data, k=1):
"""
k近傍法で x の異常度を計算(二乗距離)
x : d次元ベクトル
xs_data : n x dのデータ行列
k : k近傍法のパラメータ
"""
dx = (xs_data - x) # xs_data と x の差のベクトル
dis = dx[:, 0] ** 2 + dx[:, 1] ** 2 # 二乗距離
dis.sort() # 要素を小さい順番に並び替える
return dis[k-1] # k-1番目の要素がk番目に近いデータ点までの距離
# テスト
knn(np.array([10, 10]), xs, k=3)
# 5.975744815455611
5. k近傍法が仮定している確率分布
さて、このブログのシリーズの流れとしては、
・・・データの背後に真の分布$p({\bf x})$ありき、そして、それを近似して$p'({\bf x})$とし、異常度を$a({\bf x})=-\log(p'({\bf x}))$で求めるべし・・・
という流れにこだわりたかったのですが、今回は、近似分布$p'({\bf x})$を考えることなく、異常度$a({\bf x})$がさっさと求まり、一件落着となっています。
しかし、あえて、この異常度$a({\bf x})$に対する近似分布$p'({\bf x})$はなんなのかと、逆に考えてみるのも意味のあることだと思います。
この点に関しましては、あまり参考になる資料がなく、私独自に考えたものになりますので、おかしいなと思われた方は、コメントなどいただけると幸いです。
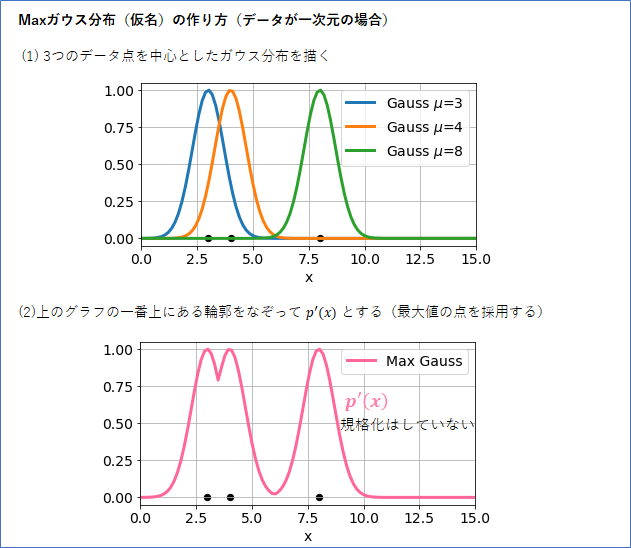
まず1次元のデータ3点 (3 と 4 と 8) で考えます。
そして、シンプルにした以下のようなガウス分布 $g(x; \mu)$ を考えます。
g(x; \mu) = \exp (-(x - \mu)^2)
分散パラメータはなし、平均パラメータ$\mu$のみがあります。積分して1にするための定数(通常は$\exp$の前にある数値です)は省略しています(なので、正確には確率分布とは言えないのですが、ここの議論では無視しても大丈夫です)。
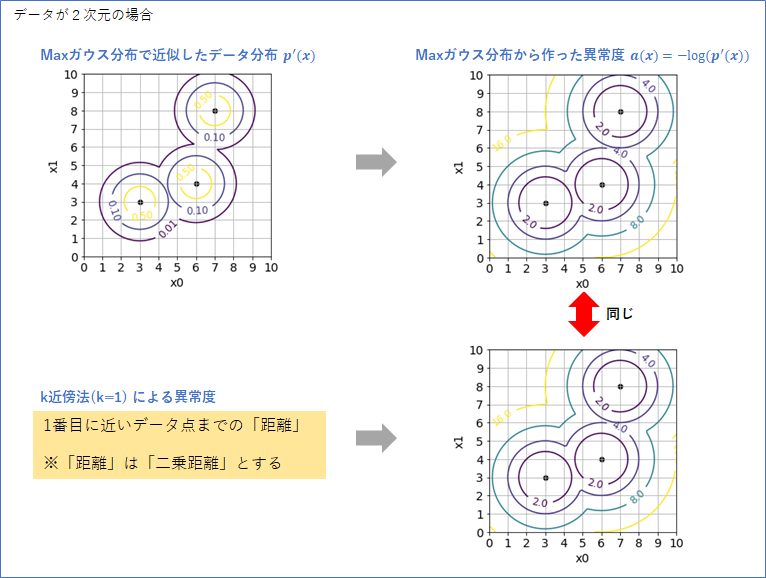
このガウス分布を使って、以下の上図ように、(1) 3つのデータ点を中心とした分布を描きます。そして、(2) グラフの一番上にある輪郭をなぞってそれを$p'(x)$とします。この$p'(x)$こそが、k近傍法(k=1)が暗に仮定している、データの近似の確率分布だと思われます。「Maxガウス分布」、とでも名付けておきましょう。
このMaxガウス分布は、確率分布は積分しても1にはならないことに注意してください(異常度を作る分には問題になりまません)。
このMaxガウス分布ですが、「混合ガウス分布(こちらが分かりやすいと思います)」をご存じの方は、それとどう違うの?と思われるかもしれませんので、その違いについて2点整理しました。
(1) まず分布そのものの形が異なります。複数のガウス分布が重なったところの$p(x)$の値は、Maxガウス分布では複数のガウス分布での値の中での「最大の点」となりますが、混合ガウス分布では、すべての「和」になります。混合ガウス分布はガウス分布を密集させると、そこでの値が高くなりますが、Maxガウス分布では、一つのガウス分布の高さより高くなることはありません。
(2) パラメータの使い方が異なります。「Maxガウス分布」の各ガウス分布の平均パラメータは、各データ点として固定です。共分散パラメータも固定です。ガウス分布の数もデータ数に一致します。「混合ガウス分布」は、各ガウス分布に対して平均パラメータと共分散パラメータを決める必要があります。ガウス分布の数もパラメータです。
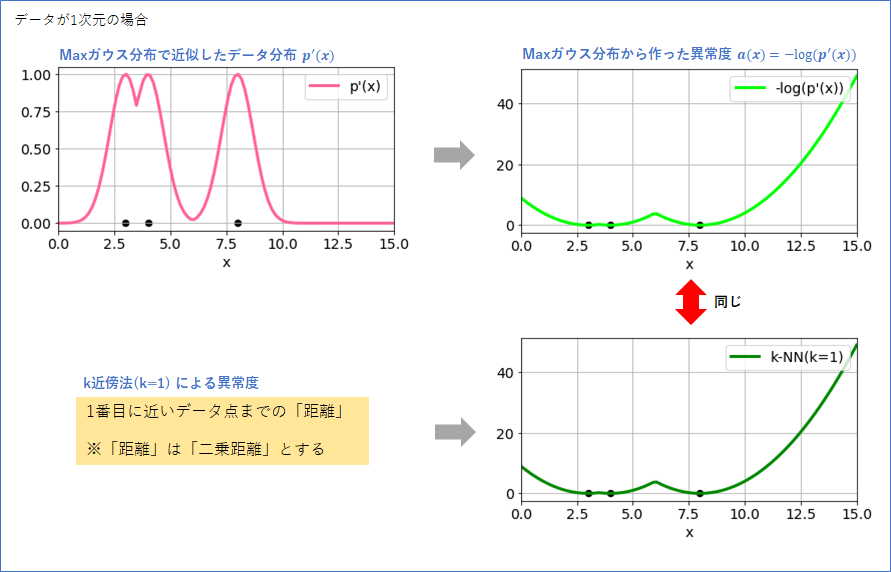
では、話を元に戻します。上記で作った「Maxガウス分布 $p'(x)$」から、異常度$a(x)=-\log (p'(x))$を求めたものが、下の右上のグラフになります。ちょうど、データのある個所で一番小さい値をとっていますので、もっともらしい形と言えるでしょう。
同じデータを使って、k近傍法(k=1)で異常度$a(x)$を求めると、右下のグラフになりました。これは、Maxガウス分布から求めた異常度と一致します。つまり、k近傍法(k=1)が暗に想定している確率確率分布は、Maxガウス分布に他ならないということです。
同様の確認を2次元データでやってみたものが下図です。この場合でも、Maxガウス分布から作った異常度と、k近傍法が作った異常度が一致しました。
よって、k近傍法(k=1)が暗に想定している確率分布は、「Maxガウス分布」と考えてよさそうです。
つまり、k近傍法というのは、データ点一つ一つにガウス分布を帽子のようにかぶせて確率分布を作っているようなものなのです。確かにそういった分布の作り方もありですね。なるほどです。ちなみに、このブログの見出しの樹氷の写真も、この分布をイメージして選びました。
6. さいごに
これで、今回の異常検知(3)はおしまいです。最後までお読みいただきありがとうございました。
ここまでは、データ点1つで異常度が判定できる問題でしたが、次は、複数点があって初めて判定できる問題を扱い、時系列データに応用することを考えたいと思います。
※2021/7/9 K氏からデータ計算量に関するコメント、K氏からはkのデータ数依存性についてのコメントをいただいたので、内容に追加させていただきました。ありがとうございました。
参考文献
[1] 井出・杉山著「異常検知と変化検知」機械学習プロフェッショナルシリーズ(講談社)