本記事の概要
Kaggleの有名な課題として「Titanic : Machine Learning from Disaster」があります。
今回は、教師あり学習の機械学習手法で分類に利用されるロジスティック回帰を学びます。
「機械学習を触ってみたいけど、データもないからどこから手を付けていいか分からない。」
そんな方にも機械学習の入門としておすすめです。
目次
1. データセットの確認
[2. データの前処理](#2. データの前処理)
3. モデルの作成(ロジスティック回帰モデル)
4. モデルの評価
5. おわりに
1. データセットの確認
今回利用するタイタニックデータをKaggleからダウンロードしていきます。
Kaggleの無料会員登録を実施し、Kaggleタイタニックデータページで今回利用する下記のデータをダウンロードして下さい。
- training set (train.csv)
- test set (test.set) ※今回は使用しません
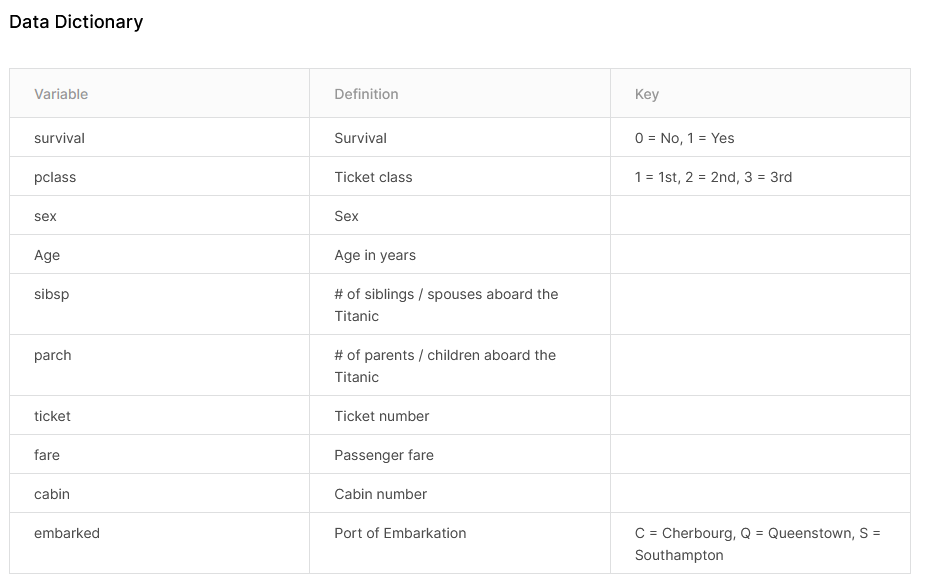
Kaggleタイタニックデータページには、データの詳細も記述されています。
タイタニックの事故での生死に加え、チケットクラスや性別などのパラメータがセットになっています。
import numpy as np
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
# matplotlibをinlineで表示するためのおまじない (plt.show()しなくていい)
%matplotlib inline
# titanic data csvファイルの読み込み
titanic_df = pd.read_csv('/データを保存したディレクトリを指定/train.csv')
# ファイルの先頭部を表示し、データセットを確認する
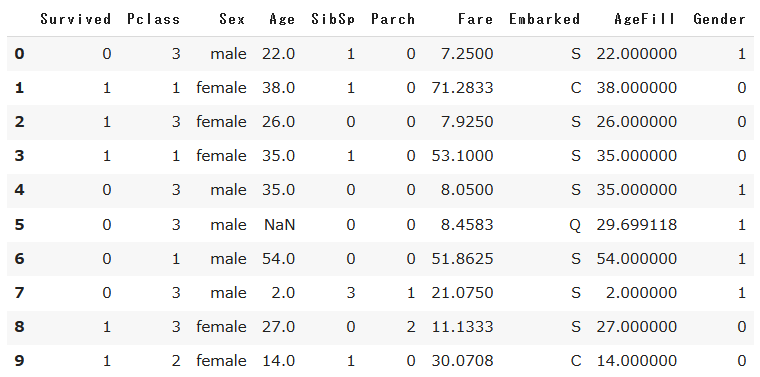
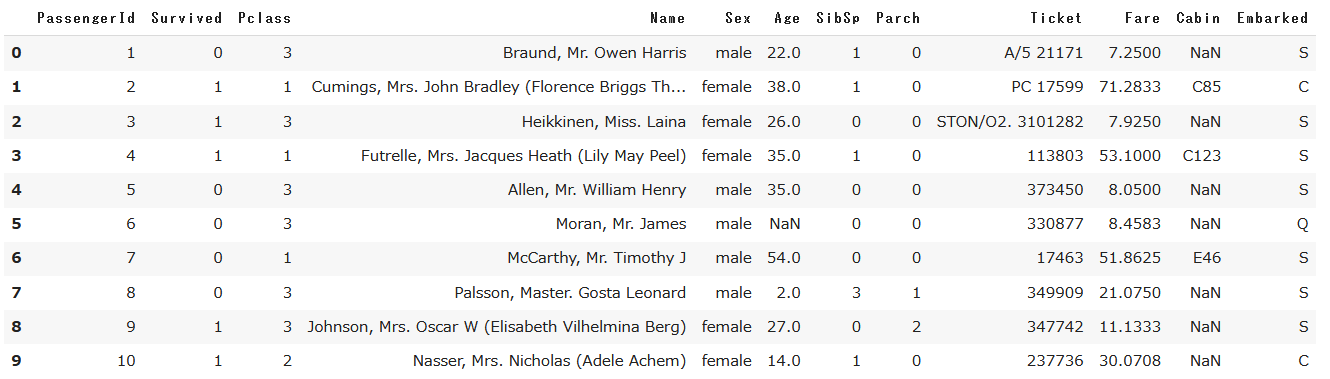
titanic_df.head(10)
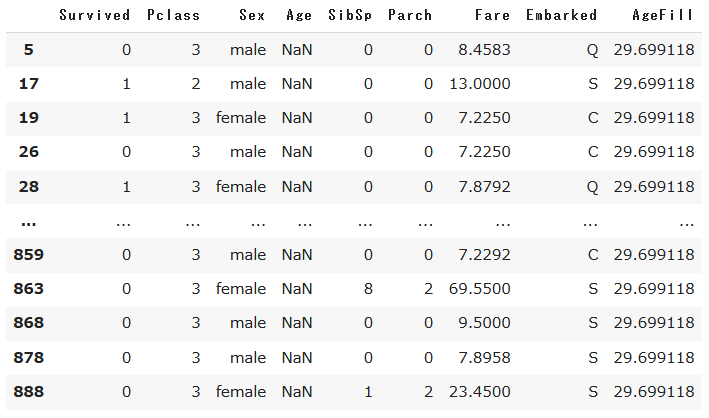
以下に、CSVの読み込みから得られた訓練データのデータフレームを示します。データを確認するとAge、Cabinに欠損値(NaN)が含まれていたりすることが分かりますね。
2. データの前処理
データフレームから確認された欠損値などの前処理をしていきましょう。
まずは、今回の分析で取り扱わないデータをデータフレームから落としていきます。(※今回は入門編のため)
# 予測に不用と考えるカラムをドロップ
titanic_df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
# 1部カラムをドロップしたデータを表示
titanic_df.head(10)
分析に不用と判断したカラムをドロップした後のデータフレームです。

次に冒頭で確認された欠損値が含まれている行を表示します。
# nullを含んでいる行を表示
titanic_df[titanic_df.isnull().any(1)].head(10)
Ageカラムの欠損値を平均値で補完します。
# Ageカラムのnullを平均値で補完し、新しくAgeFillカラムを作成
titanic_df['AgeFill'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())
# 再度nullを含んでいる行を表示(Ageのnullは補完されている)
titanic_df[titanic_df.isnull().any(1)]
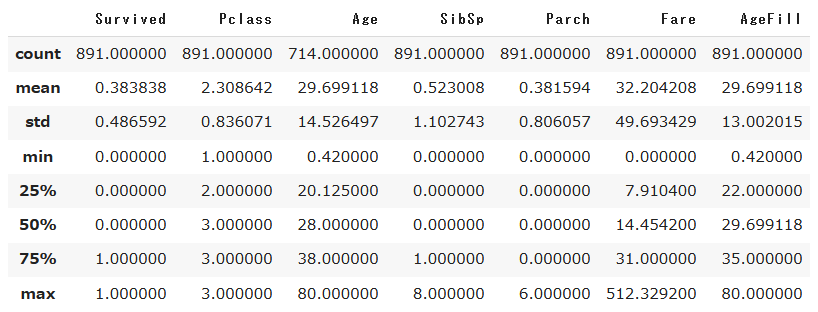
また、要約統計量を表示させてみます。
titanic_df.describe()
これにより各パラメータのデータ範囲がざっくりとつかめます。例えば、Survivedの平均値が0.38ですので、半分以上が死んでいるということですね…
3. モデルの作成(ロジスティック回帰モデル)
3.1. 1変数のみを用いた生死の判別
まずは1変数のみを利用してロジスティック回帰モデルを学習させてみましょう。scikit-learnで、ロジスティック回帰を実装するには、sklearn.linear_model.LogisticRegressionを利用します。
# 運賃(Fare)だけのリストを作成
data1 = titanic_df.loc[:,["Fare"]].values
print(data1.shape) # データ形状の確認
> (891, 1)
# ターゲットである生死フラグのみのリストを作成
label1 = titanic_df.loc[:,["Survived"]].values
from sklearn.linear_model import LogisticRegression
# ロジスティック回帰モデルのオブジェクト生成
model = LogisticRegression()
# モデルの学習
model.fit(data1, label1)
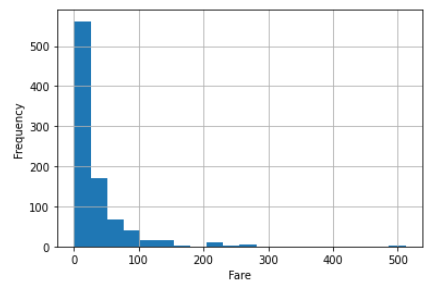
1変数を用いて学習が完了しました。この学習モデルを用いて生死を判別してみましょう。前章で確認した要約統計量から、運賃(Fare)の範囲が0(min)~512.3(max)、全体の75%が31以下の運賃で乗車していることが分かっています。(文章だけだとイメージをしづらいので、ヒストグラムで確認してみると以下の通り。)
plt.hist(data1,bins=20)
plt.ylabel('Frequency')
plt.xlabel('Fare')
plt.grid()
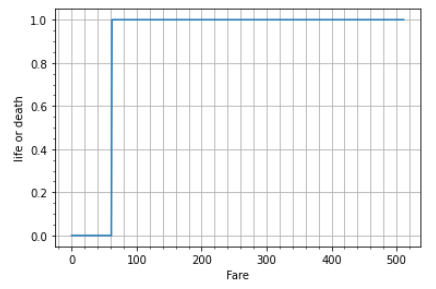
この運賃の情報を念頭に、今回学習させたモデルで運賃範囲0~512.3のどこから生死が分かれているか、結果をグラフ化します。
n = np.arange(0,512,1)
result = [] # 結果を入れるリストを用意
for fare in range(0,512,1):
result.append(model.predict([[fare]]))
# 結果をグラフ化
plt.plot(n,result)
plt.ylabel('life or death')
plt.xlabel('Fare')
plt.minorticks_on()
plt.grid(which = "both", axis="x")
plt.grid(axis="y")
このグラフから運賃が約60以上で生死が分かれるモデルが得られたことが分かります。運賃の分布から、大半の人がなくなっている結果になりますね。また、運賃が高いほど生き残っている、と予測されるとも言えますね(感覚的に傾向は合致していると思います…)。
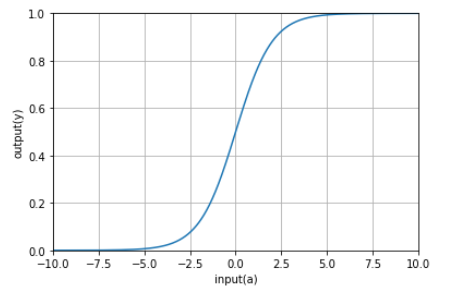
このグラフのようにロジスティック回帰は分類の機械学習手法にあたるので、入力に対して最終的な予測結果は分類結果(0 or 1)が得られます。ただ、実際モデルの中では、入力の線形結合結果をシグモイド関数に入力し、出力として0~1の連続値を得て、シグモイド関数の値(=確率)が0.5以上であれば1、未満であれば0と予測する、という処理が組み込まれています。この予測結果と教師データ(タイタニックデータでいう生死データ)の誤差を学習していくことで、精度を高めているわけですね。
このような処理がなされているので、scikit-learnのロジスティック回帰のモジュールには、分類結果(0、1)だけでなく、分類確率も出力するメソッドが実装されています。
原理をより詳しく知りたい方は、以下の方の記事が参考になりました。
<参考になる解説記事>
・ロジスティック回帰
# 運賃が62の場合の分類結果と確率を示す
model.predict([[62]])
> array([1])
model.predict_proba([[62]])
> array([[0.49978123, 0.50021877]]) # 0の確率、1の確率
# 運賃が10の場合の分類結果と確率を示す
model.predict([[10]])
> array([0])
model.predict_proba([[10]])
> array([[0.68769203, 0.31230797]]) # 0の確率と、1の確率
# シグモイド関数で処理されていることの確認
# モデルで学習された重み
w_0 = model.intercept_[0]
w_1 = model.coef_[0,0]
def sigmoid(x):
return 1 / (1+np.exp(-(w_1*x+w_0)))
x_range = np.linspace(-1, 500, 3000)
plt.plot(data1, model.predict_proba(data1), 'o', label='predict_ploba') # 各運賃での生死の確率の計算(0と1の確率どちらも算出される)
plt.plot(x_range, sigmoid(x_range), '-', color='black', label='sigmoid') # 自作したシグモイド関数のプロット
plt.ylabel('probability')
plt.xlabel('Fare')
plt.legend(loc=2)
plt.grid()
運賃が62の場合は、生死がほぼ同じ確率である一方で、運賃が10の場合は死亡確率が69%程度であることが分かります。
また、作成した生存確率のグラフを見ると、自作したシグモイド関数と、各運賃に対してクラス=1を分類する確率がぴったり一致していることが見て取れます。前述の通り、ロジスティック回帰モデルの内部でシグモイド関数が機能していることが分かりましたね。本モデルの精度に関しては、4章以降で検証していきます。
3.2. 2変数を用いた生死の判別
これまで1変数を用いて生死の判別を行ってきましたが、続いて変数を増やしたモデルを作成してみましょう。
欠損値処理をしたデータフレームを改めて確認します。性別(Sex)に着目すると、データが数値ではなく、文字列になっています。モデルの学習のためには数値である必要があるため、データを変換しましょう。
# 性別データの数値変換
titanic_df['Gender'] = titanic_df['Sex'].map({'female':0, 'male':1}).astype(int)
titanic_df.head()
一番右の列に新たにデータ列を加えました。次に乗客の社会階級(Pclass)に着目していきましょう。直観ではありますが、社会階級が高い男性、社会階級が低い女性、といった性別と階級の組み合わせの特徴量をつくると、生死の確率と相関のありそうなデータが得られそうです。そこで、本仮説を基に、新たな特徴量を作成してみます。(※エンジニアとして働いているとデータを加工することは良くあります。)
# 社会階級と性別を組み合わせた新たな特徴量の作成
titanic_df['Pclass_Gender'] = titanic_df['Pclass'] + titanic_df['Gender']
titanic_df.head()
この作成した特徴量(Pclass_Gender)を入力データとして使用していくので、不要なデータを削除しましょう。
titanic_df = titanic_df.drop(['Pclass', 'Sex', 'Gender','Age'], axis=1)
titanic_df.head()
作成した特徴量を基に生死の分布を可視化してみましょう。
np.random.seed = 0
xmin, xmax = -5, 85
ymin, ymax = 0.2, 4.5
# 生存者と死亡者の分類
index_survived = titanic_df[titanic_df["Survived"]==0].index
index_notsurvived = titanic_df[titanic_df["Survived"]==1].index
from matplotlib.colors import ListedColormap
fig, ax = plt.subplots()
# AgeFillとPclassGenderのグラフ、生存者と死亡者を別々にプロット
sc = ax.scatter(titanic_df.loc[index_notsurvived, 'AgeFill'], titanic_df.loc[index_notsurvived, 'Pclass_Gender'] + (np.random.rand(len(index_notsurvived))-0.5)*0.1, color='r', label='NotSurvived', alpha=0.3)
sc = ax.scatter(titanic_df.loc[index_survived, 'AgeFill'], titanic_df.loc[index_survived, 'Pclass_Gender'] + (np.random.rand(len(index_survived))-0.5)*0.1, color='b', label='Survived', alpha=0.3)
ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass_Gender')
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.legend(bbox_to_anchor=(1.4, 1.03))
plt.grid()
このグラフより、社会階級が高い女性(=1)の生存率が極めて高い傾向があると言えます。また、値が小さいほど生存率が高そうなので、社会階級が低いより高いほうが、男性より女性が、生存率が高いことが分かり、仮説の確からしさがグラフからも見て取れます。また、x軸に年齢を取っており、年齢からも子ども(10~20歳)の生存率が高いことも分かりますね。
グラフから、おおよその傾向がつかめたので、ロジスティック回帰モデルを作成していきましょう。
# AgeFillとPclass_Genderだけのリストを作成
data2 = titanic_df.loc[:, ["AgeFill", "Pclass_Gender"]].values
# 生死フラグのみのリストを作成
label2 = titanic_df.loc[:,["Survived"]].values
# データの確認
print(data2.shape)
> (891, 2)
print(data2)
> [[22. 4. ]
[38. 1. ]
[26. 3. ]
...
[29.69911765 3. ]
[26. 2. ]
[32. 4. ]]
model2 = LogisticRegression()
model2.fit(data2, label2)
ロジスティック回帰モデルの学習ができました。続いて、モデルで予測値を算出してみましょう。
# 10歳、社会階級の高い女性
model2.predict([[10,1]])
> array([1]) # 生存
model2.predict_proba([[10,1]])
> array([[0.03754749, 0.96245251]]) # 96%生存
妥当な予測結果が得られました。年齢が若く、社会階級の高い女性ほど、生存確率が高そうです。
3.3 分類の境界線の可視化
ロジスティック回帰の理解を深めるため、この予測結果がどのように算出されているか分類の境界線を可視化してみましょう。今回得たいのは、AgeFillとPclassGenderの2変数生死分布の分類境界線です(前述の赤と青のプロットグラフ参照)。
3.1.で前述したように、ロジスティック回帰は、入力の線形結合結果をシグモイド関数に入力し、出力として0~1の連続値=確率を得て、シグモイド関数の値(=確率)が0.5以上であれば1、未満であれば0と予測するモデルでした。変数をx1、x2(今回の場合はx1:AgeFill、x2:Pclass_Gender)とし、重みをw1、w2、バイアスをbと置くと、ロジスティック回帰の流れは、以下の図のようになります。
図で書くと分かりやすいですね。これを式で書くと、
a = w_1 \cdot x_1 + w_2 \cdot x_2 + b\\
y = \frac{1}{1+\exp(-a)}
と表されます。ここで、aは実数全体(-∞~∞)を取りますが、yはシグモイド関数なので0~1の範囲になります。有名なシグモイド関数のグラフを見ると、この説明が理解できるかと思います。
ここで、このシグモイド関数の値(=確率)が、≧0.5であればクラス1、≦0.5であればクラス2に分類されるので、このyの分類境界線はy=0.5になり、yへの入力aの分類境界線はa=0になると言えます。グラフをわかりやすくすると以下の通り。
分類の境界線がa=0であることが理解できたところで、先ほどの式に戻ります。今回得たいのは、x1(AgeFill)とx2(PclassGender)の2変数グラフの生死分類の境界線なので、境界線のx1とx2の関係です。つまり、
0 = w_1 \cdot x_1 + w_2 \cdot x_2 + b\\
x_2 = -(w_1 \cdot x_1 + b)/w_2
が、境界線の式になります。それでは実際のデータで境界線を可視化していきましょう。
fig, ax = plt.subplots()
sc = ax.scatter(titanic_df.loc[index_notsurvived, 'AgeFill'], titanic_df.loc[index_notsurvived, 'Pclass_Gender'] + (np.random.rand(len(index_notsurvived))-0.5)*0.1, color='r', label='NotSurvived', alpha=0.3)
sc = ax.scatter(titanic_df.loc[index_survived, 'AgeFill'], titanic_df.loc[index_survived, 'Pclass_Gender'] + (np.random.rand(len(index_survived))-0.5)*0.1, color='b', label='Survived', alpha=0.3)
ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass_Gender')
xmin, xmax = -5, 85
ymin, ymax = 0.2, 4.5
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
x1 = xmin
x2 = xmax
y1 = -1*(model2.intercept_[0]+model2.coef_[0][0]*xmin)/model2.coef_[0][1]
y2 = -1*(model2.intercept_[0]+model2.coef_[0][0]*xmax)/model2.coef_[0][1]
ax.plot([x1, x2], [y1, y2], 'k--', label='border')
ax.legend(bbox_to_anchor=(1.4, 1.03))
plt.grid()
境界線と生死分布をみると、概ね分類出来ていることが分かります。ただ、AgeFillが20~30、PclassGenderが3~4のあたりを見ると、実際は生存者であっても、死亡と予測している点がありますね。そこで、次にこのモデルの性能を評価していきたいと思います。
4. モデルの評価
先ほど作成した決定係数R^2を確認してみましょう。
from sklearn.model_selection import train_test_split
# 訓練データとテストデータの分割
traindata1, testdata1, trainlabel1, testlabel1 = train_test_split(data1, label1, test_size=0.2)
traindata2, testdata2, trainlabel2, testlabel2 = train_test_split(data2, label2, test_size=0.2)
eval_model1 = LogisticRegression()
eval_model2 = LogisticRegression()
predictor_eval1 = eval_model1.fit(traindata1, trainlabel1).predict(testdata1)
predictor_eval2 = eval_model2.fit(traindata2, trainlabel2).predict(testdata2)
# 1変数のみを用いたモデルの評価
print(eval_model1.score(traindata1, trainlabel1))
print(eval_model1.score(testdata1, testlabel1))
> 0.6643258426966292 # 訓練データのR^2
> 0.664804469273743 # 検証データのR^2
# 2変数を用いたモデルの評価
print(eval_model2.score(traindata2, trainlabel2))
print(eval_model2.score(testdata2, testlabel2))
> 0.7682584269662921 # 訓練データのR^2
> 0.7988826815642458 # 検証データのR^2
2変数を用いたときの決定係数R^2が大きいのでより精度がいいモデルが得られていると言えそうです。ただ、このR^2という指標は分類性能を測る一つの指標でしかないため、アプリケーションによっては、R^2が高くても本当に得たいモデルが得られていない場合もあります。そこで、混同行列(Confusion Matrix)で性能を評価してみましょう。
4.1. 混同行列
混同行列とは、2クラス分類の評価結果を最も包括的に表現できる方法で、予測の分類と教師データの分類のマトリックスで表されます。
間違い(False)としては、偽陰性(FN)、偽陽性(FP)があります。偽陰性の具体例としては、健康な患者を陽性に分類してしまうことが挙げられ、この場合健康な患者に無駄な費用や心労をかけてしまうことになります。一方、偽陽性の具体例としては、病気患者を陰性と分類してしまうことで、この場合必要な検査や治療が受けられず、最悪死に至る可能性があります。この例からも分かる通り、アプリケーションの要件次第で、偽陽性、偽陰性の重みが変わってきます。
より詳しい解説は、以下の記事が参考になりました。
<参考になる解説記事>
・混同行列
それでは実際に混同行列を求めてみましょう。
from sklearn.metrics import confusion_matrix
confusion_matrix1 = confusion_matrix(testlabel1, predictor_eval1)
confusion_matrix2 = confusion_matrix(testlabel2, predictor_eval2)
# 1変数のみを用いたモデルのグラフ
fig = plt.figure(figsize = (7,7))
sns.heatmap(
confusion_matrix1,
vmin=None,
vmax=None,
cmap="Blues",
center=None,
robust=False,
annot=True, fmt='.2g',
annot_kws=None,
linewidth=0,
linecolor='White',
cbar=True,
cbar_kws=None,
cbar_ax=None,
square=True, ax=None,
mask=None)
# 2変数を用いたモデルのグラフ
fig = plt.figure(figsize = (7,7))
sns.heatmap(
confusion_matrix2,
vmin=None,
vmax=None,
cmap="Blues",
center=None,
robust=False,
annot=True, fmt='.2g',
annot_kws=None,
linewidths=0,
linecolor='white',
cbar=True,
cbar_kws=None,
cbar_ax=None,
square=True, ax=None,
mask=None)
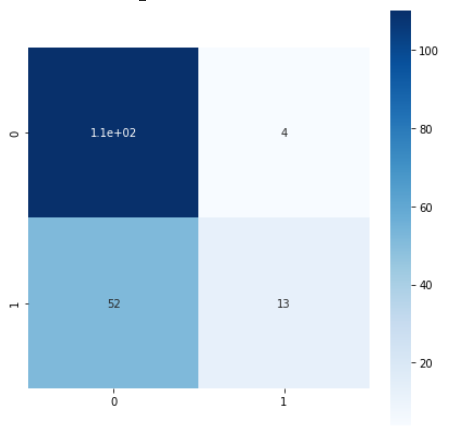
TP=13、実際に生存者(=1)を生存(=1)と予測
FP=4、実際は死亡者(=0)で生存(=1)と予測
FN=52、実際は生存者(=1)で死亡(=0)と予測
TN=110、実際に死亡者(=0)を死亡(=0)と予測
TP=46、実際に生存者(=1)を生存(=1)と予測
FP=5、実際は死亡者(=0)で生存(=1)と予測
FN=32、実際は生存者(=1)で死亡(=0)と予測
TN=96、実際に死亡者(=0)を死亡(=0)と予測
2変数を用いたモデルのほうが、TPが圧倒的に大きいですね。1変数では運賃、2変数では年齢、性別をパラメータとして利用したので、生存には年齢と性別の寄与が大きいと考えられます。
この混同行列を用いた以下の評価指標を計算してみます。
精度 \quad Accuracy = \frac{TP+TN}{TP+TN+FP+FN} \\
適合率 \quad Precision = \frac{TP}{TP+FP} \\
再現率 \quad Recall = \frac{TP}{TP+FN} \\
f値 \quad F = 2 × \frac{適合率×再現率}{適合率+再現率} \\
from sklearn import metrics
print(metrics.classification_report(testlabel1, predictor_eval1))
> precision recall f1-score support
0 0.66 0.93 0.77 110
1 0.68 0.25 0.36 69
accuracy 0.66 179
macro avg 0.67 0.59 0.57 179
weighted avg 0.67 0.66 0.61 179
print(metrics.classification_report(testlabel2, predictor_eval2))
> precision recall f1-score support
0 0.79 0.91 0.85 110
1 0.81 0.62 0.70 69
accuracy 0.80 179
macro avg 0.80 0.77 0.78 179
weighted avg 0.80 0.80 0.79 179
1変数のみを用いたモデルと2変数を用いたモデルの生存者の再現率を比較すると、0.25から0.62に大きくなっていますが、2変数を用いたモデルでもまだ不十分な値であることが分かります。
前章で示したAgeFillとPclassGenderのグラフにおいて、生存者であっても死亡と予測している点が多かったことからもこの値は妥当であることが分かります。
5. おわりに
本記事では、ロジスティック回帰を活用して分類問題を解き、混同行列を用いてモデルの評価を実施しました。
実装に焦点を当てたので、今後は数学的背景などの解説記事を書いていきたいと思います。
機械学習入門のリンク
今後も引き続き機械学習の実装入門を記事にしていきます。
参考にどうぞ。
・線形回帰
・非線形回帰
・k-近傍法
・ロジスティック回帰 本記事
・主成分分析
・K-means
・サポートベクターマシン ※今後更新予定