本記事の概要
scikit-learnのボストンの住宅価格データセットを活用し、ボストンの住宅価格を予測するモデルを作成します。
教師あり学習の機械学習手法で回帰に利用される線形回帰モデルを実践的に学びます。
「機械学習を触ってみたいけど、データもないからどこから手を付けていいか分からない。」
そんな方にも機械学習の入門としておすすめです。
目次
1. データセットの確認
2. データの可視化
3. モデルの作成(線形モデル)
4. モデルの検証
5. モデルの改良
6. 残差プロット
7. おわりに
1. データセットの確認
まずはじめに、ボストンの住宅価格データセットをscikit-learnのライブラリからダウンロードをしましょう。
ダウロード後にpandasを活用してデータの確認をします。
import pandas as pd
from sklearn.datasets import load_boston
# ボストンデータセットの読み込み
boston = load_boston()
# ボストンデータセットのデータフレームの作成
df = pd.DataFrame(boston.data, columns=boston.feature_names)
# 目的変数(PRICE)をデータフレームに結合
df['PRICE'] = np.array(boston.target)
# ボストンデータセットの変数の説明の表示
print(boston['DESCR'])
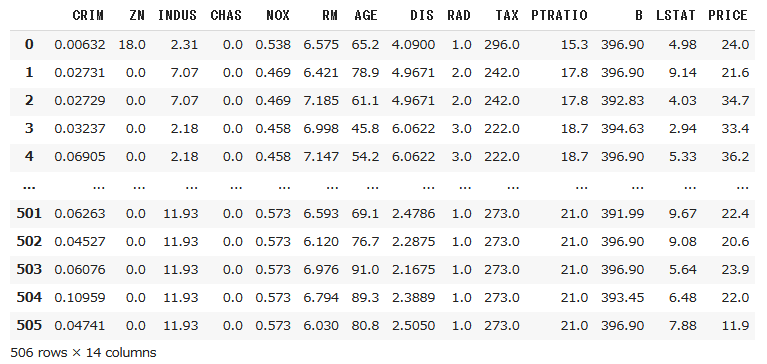
データフレームの出力結果は以下の通りです。
レコード数は506個、変数は14個(うち1個は目的変数(PRICE))であることが確認できます。
また、DESCRに各変数(目的変数以外)の概要が記述されているので、表示をさせてみます。
(※日本語要約は理解をしやすくするため追記しています)
Data Set Characteristics:
:Attribute Information (in order):
- CRIM per capita crime rate by town :犯罪発生率
- ZN proportion of residential land zoned for lots over 25,000 sq.ft. :25000平方フィート以上の住宅区間の割合
- INDUS proportion of non-retail business acres per town :非小売業の土地面積の割合
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) :チャールズ側沿いかどうか(1:川沿い、0:川沿いではない)
- NOX nitric oxides concentration (parts per 10 million) :窒素酸化物の濃度
- RM average number of rooms per dwelling :一戸あたりの平均部屋数
- AGE proportion of owner-occupied units built prior to 1940 :1940年よりも前に建てられた家屋の割合
- DIS weighted distances to five Boston employment centres :ボストンの主な雇用圏までの重み付き距離
- RAD index of accessibility to radial highways :幹線道路へのアクセス指数
- TAX full-value property-tax rate per $10,000 :10000ドルあたりの所得税率
- PTRATIO pupil-teacher ratio by town :教師あたりの生徒の数
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town :アフリカ系アメリカ人居住者の割合
- LSTAT % lower status of the population :低所得者の割合
2. データの可視化
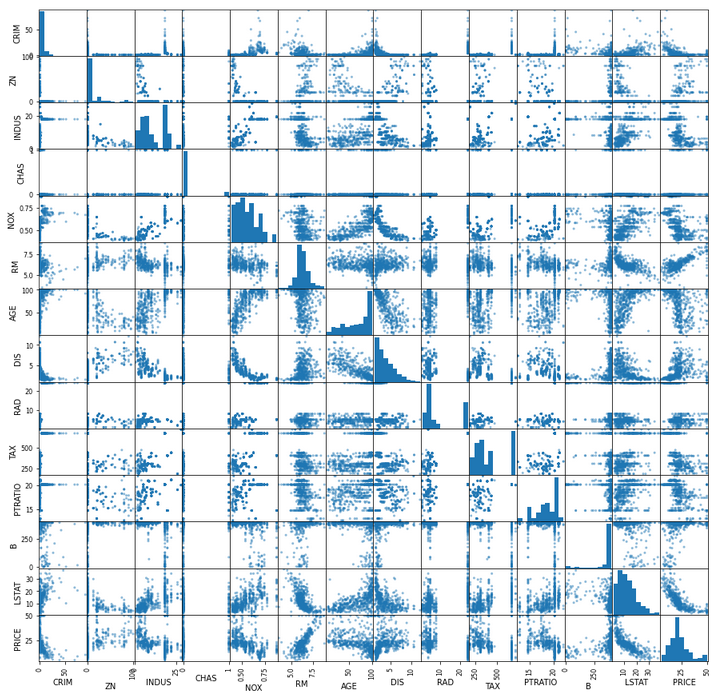
次に各変数間のペアプロットを表示し、データの相関を確認してみましょう。
データを可視化することで、あらかじめデータ間の相関が予測されたり、異常な点を見つけたりすることができます。
# pandasのscatter_matrix関数を使いペアプロットを表示
from pandas.plotting import scatter_matrix
fig = pd.plotting.scatter_matrix(df, figsize=(15,15))
目的変数(PRICE, 一番下の行)と各説明変数に着目してみると、RM(一戸あたりの平均部屋数, 6列目)などは明らかな右肩上がりの関係を持つことが確認できます。
当たり前ですが、部屋数が増えると住宅価格が上がる、という関係があることが分かりますね。
その他にも、犯罪発生率(CRIME, 1列目)が低いと、低所得者の割合が低い(LSTAT, 13列目)と、住宅価格は高くなる関係があることも分かります。
3. モデルの作成(線形モデル)
それではいよいよモデルの作成に移っていきましょう。
今回は、線形モデルを作成し、住宅価格の予測をしてみます。
「2.データの可視化」で相関が見られた2変数(RM, CRIME)を活用してモデルを作成します。
from sklearn.model_selection import train_test_split
# 説明変数の抽出(CRIME、RM)
data = df.loc[:,['CRIM','RM']].values
# 目的変数の抽出
target = df.loc[:,'PRICE'].values
# データの分割(訓練データ、検証データ)
X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=0)
# sklearnモジュールからLinearRegressionをインポート
from sklearn.linear_model import LinearRegression
# 線形モデルのオブジェクト生成
model = LinearRegression()
# モデルの学習
model.fit(X_train, y_train)
これで線形モデルの学習が終わりました。
試しにモデルを活用して住宅価格を予測してみましょう。
例えば、犯罪発生率(CRIM)=0.2、部屋数(RM)=6とすると、下記の住宅価格の予測値が得られました。
model.predict([[0.2, 6]])
> array([20.94426001])
一方で、犯罪発生率(CRIM)=10、部屋数(RM)=6のように犯罪発生率を大きくしてみると、住宅価格が約$3,000安くなると予測されました。
model.predict([[10, 6]])
> array([17.81097374])
4. モデルの検証
続いて作成したモデルの性能を評価します。
# 作成したモデルから予測(学習用、検証用モデル使用)
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
# 誤差の計算
from sklearn.metrics import mean_squared_error
# 平均二乗誤差:小さいほど誤差の小さなモデルと言える
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 決定係数:回帰式の適合性の指標(1に近いほど良い)
print('R^2 Train : %.3f, Test : %.3f' % (model.score(X_train, y_train), model.score(X_test, y_test)))
> MSE Train : 37.004, Test : 44.945
> R^2 Train : 0.566, Test : 0.450
今回作成した2変数の線形重回帰モデルは、誤差が大きく、決定係数≦0.5なので、適合度が低いことがわかります。
2変数だけだと正確な予測が出来ないということですね。
5. モデルの改良
2変数だけだと予測精度が低いので、単純に説明変数を増やしてみましょう。
# 説明変数の抽出(13個の変数)
data = df.loc[:,'CRIM':'LSTAT'].values
print(data2.shape)
> (506, 13)
# 以下は先ほどのデータ処理と同様の処理を実施
X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=0)
model = LinearRegression()
model.fit(X_train, y_train)
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
print('R^2 Train : %.3f, Test : %.3f' % (model.score(X_train, y_train), model.score(X_test, y_test)))
> MSE Train : 19.641, Test : 29.782
> R^2 Train : 0.770, Test : 0.635
先ほどの2変数のモデルと比較し、説明変数が増えたことにより誤差が小さくなり、決定係数≧0.5と適合度も向上させることができました。
ただし、精度としてはさらに向上させる余地がありそうですね。
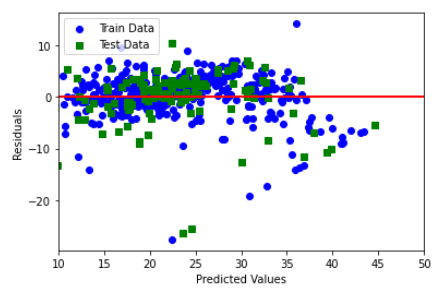
6. 残差プロット
モデルの改良、および検証まで終わったので、残差プロットを作成して外れ値を確認してみましょう。
import matplotlib.pyplot as plt
plt.scatter(y_train_pred, y_train_pred - y_train, c = 'blue', marker = 'o', label = 'Train Data')
plt.scatter(y_test_pred, y_test_pred - y_test, c = 'green', marker = 's', label = 'Test Data')
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y = 0, xmin = -10, xmax = 50, lw = 2, color = 'red')
plt.xlim([10,50])
plt.show()
プロットから、どうやら右下の方に外れ値が存在していることが確認されます。
綺麗な直線であることからも、何かしらデータに問題がありそうですね。
記事には示しませんが、改良前の2変数で作成したモデルにも同様の外れ値が見られたので、CRIM、RMとPRICEの関係を確認します。
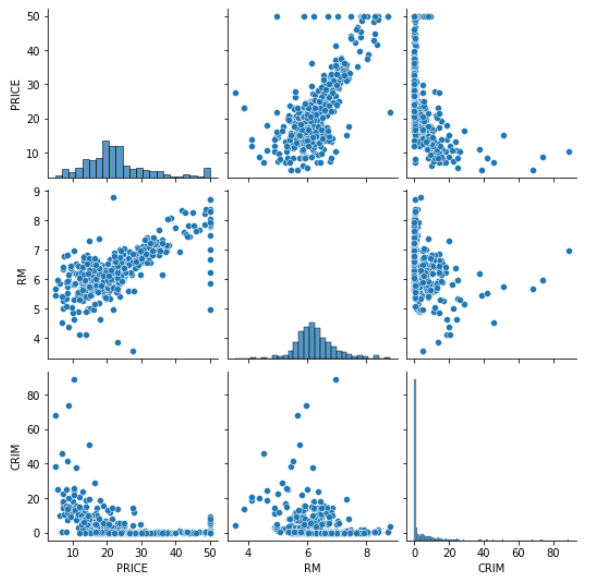
import seaborn as sns
pg = sns.pairplot(df[['PRICE','RM']])
散布行列図を確認すると、どうやらPRICEの上限が50に設定されていることが分かります。
このようなデータの制限、偏りが原因で外れ値が出てしまったと考えられます。
7. おわりに
今回は、ボストンの住宅価格データセットを用いて、住宅価格の線形回帰モデルを作成しました。
変数を増やすことで精度を上げることができましたが、更なる精度向上には、データの前処理の工夫やモデルの変更等が必要になると考えられます。
機械学習入門のリンク
今後も引き続き機械学習の実装入門を記事にしていきます。
参考にどうぞ。
・線形回帰モデル 本記事
・非線形回帰モデル
・k-近傍法
・ロジスティック回帰モデル
・主成分分析
・K-means
・サポートベクターマシン ※今後更新予定