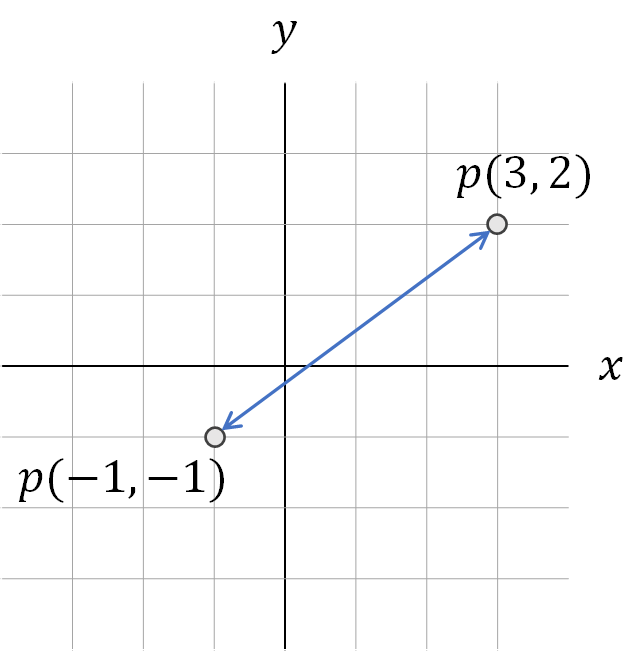本記事の概要
最も単純な学習アルゴリズムであるk-近傍法(k-NN:k-nearest neighbor)を用いて簡単な分類問題を解き、実践的に使い方を学びましょう。
目次
1. k-近傍法(k-NN)の概要
2. データの作成
3. k-近傍法による分類
4. おわりに
1. k-近傍法(k-NN)の概要
k-最近傍法は教師あり学習の分類問題に利用される機械学習手法です。最近傍のデータをk個取ってきて、それらがもっとも多く所属するクラスに分類します。要するに、多数決をしているわけです。kの数は任意に決められるハイパーパラメータであり、kの数が小さすぎると外れ値(ノイズ)に弱く、多すぎると精度が悪くなります。
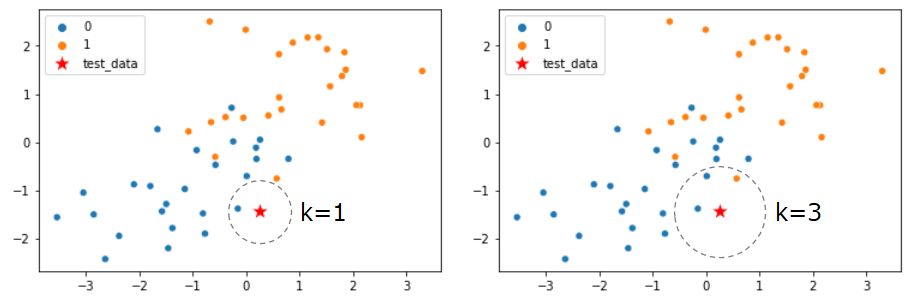
k-近傍法のイメージ図です。テストデータを赤い星のプロットで示しています。
テストデータから、訓練データまでの距離を測るのは、一般的にユークリッド距離を使います。ユークリッド距離とは、下記図のように人が定規で2点間を測る距離のことを指します。
ユークリッド距離を式で表すと下記の通りです。
p = (p_1, p_2, \cdots , p_n), q = (q_1, q_2, \cdots , q_n)\\
d(p,q)=\sqrt{(q_1-p_1)^2 + (q_2-p_2)^2 + \cdots + (q_n-p_n)^2} = \sqrt{\sum_{i=1}^{n} (q_i-p_i)^2}
上記図のプロットp,qを計算してみると、
d(p,q) = \sqrt{(3-(-1))^2+(2-(-1))^2} = 5
となりますね。
この距離を用いることでテストデータから各訓練データの距離を測り、距離が近いk個の訓練データのラベルで一番多いクラスに分類するのが、k-近傍法のアルゴリズムになります。
2. データの作成
まずはじめにnumpyを活用して分析するデータを作成していきましょう。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# クラス0、1に対応するデータ点の作成
x0 = np.random.normal(size=50).reshape(-1, 2) - 1 #(-1, -1)を中心とした正規分布
x1 = np.random.normal(size=50).reshape(-1, 2) + 1 #(1, 1)を中心とした正規分布
X_train = np.concatenate([x0, x1])
# 教師データの作成
y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
# データ形状の確認
print("x0:{}, x1:{}, X_train:{}, y_train:{}".format(x0.shape, x1.shape, X_train.shape, y_train.shape))
> x0:(25, 2), x1:(25, 2), X_train:(50, 2), y_train:(50,)
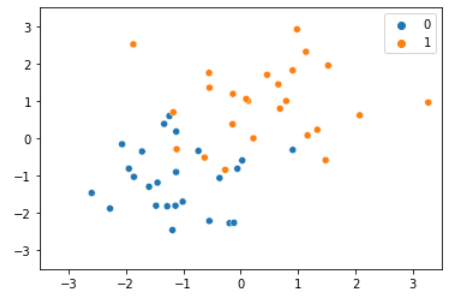
クラス0とクラス1のデータ点がそれぞれ25点ずつあります。グラフを可視化してみましょう。
sns.scatterplot(X_train[:,0], X_train[:,1], hue=y_train)
plt.xlim(-3.5, 3.5)
plt.ylim(-3.5, 3.5)
3. k-近傍法による分類(k-近傍法による分類)
それでは作成したモデルを学習させ、新たな点に対する分類問題を解いてみましょう。
# 予測したいデータ点の作成
x = np.random.normal(size=2).reshape(-1, 2)
print(x)
> [[-0.56838004 -1.52474231]]
from sklearn.neighbors import KNeighborsClassifier
# kの設定
n_neighbors = 3
# モデルの学習
knc = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X_train, y_train)
# テストデータの分類予測
y_pred = knc.predict(x)
print(y_pred)
> [0] # 予測結果=クラス0
# 可視化
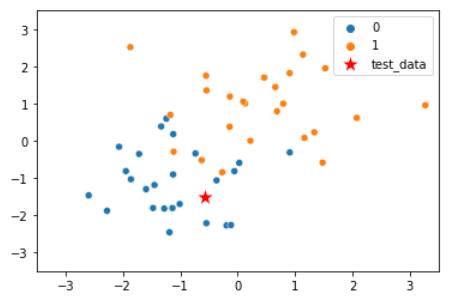
sns.scatterplot(X_train[:,0], X_train[:,1], hue=y_train)
sns.scatterplot(x[:,0], x[:,1], color='r', marker='*', s=300, label='test_data')
予測したいデータ点を赤星でプロットしていますが、予測結果(y_pred)がクラス0に分類されており、グラフからも妥当な結果であることが分かります。
冒頭でハイパーパラメータkについて触れましたが、kが分類境界に与える影響を可視化して確認してみましょう。
xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
X_test = np.array([xx0, xx1]).reshape(2, -1).T
fig, axes = plt.subplots(1, 5, figsize=(25,4))
for i, ax in zip(range(5), axes.flat):
n_neighbors = i*2 + 1
knc = KNeighborsClassifier(n_neighbors=n_neighbors).fit(X_train, y_train)
y_pred = knc.predict(X_test)
sns.scatterplot(X_train[:, 0], X_train[:, 1], hue=y_train, ax=ax)
axes[i].contourf(xx0, xx1, y_pred.reshape(100, 100).astype(dtype=np.float), alpha=0.2, levels=np.linspace(0, 1, 3), cmap='bwr')
axes[i].set_title('n_neighbors={:.0f}'.format(n_neighbors))
plt.show()
k=1~k=9のときの分類境界を示しています。k=1のときはクラス0の中にクラス1の分類範囲があることが分かり、分類境界が複雑になり、訓練データに過剰適合する結果になります(汎化性能が低い)。kを増やしていくと境界がなめらかになっていき単純なモデルになっていくと言えます。
4. おわりに
本記事では、最も単純な学習アルゴリズムであるk-近傍法(k-NN:k-nearest neighbor)を用いて簡単な分類問題を解きました。kの値を変えることで、分類モデルの複雑さを制御できることを学びました。
機械学習入門のリンク
今後も引き続き機械学習の実装入門を記事にしていきます。
参考にどうぞ。
・線形回帰モデル
・非線形回帰モデル
・k-近傍法 本記事
・ロジスティック回帰モデル
・主成分分析
・K-means
・サポートベクターマシン ※今後更新予定