本記事の概要
エンジニアとして働いていると、実験データを回帰分析して所望の特性を得るためのパラメータの設計をする、という場面に直面することがあると思います。
所望の特性とパラメータが線形の関係であれば、線形回帰モデルで予測式が得られますが、物理式の中には、特性とパラメータの関係が、2次関数や指数関数、三角関数など、線形では表されない非線形な場合も多々あり、精度の良い回帰式を得るためには線形回帰モデルだと不十分な場合があります。
今回は、numpyにより非線形データを自作し、非線形回帰モデルを活用して分析することで、実践的に学びたいと思います。
目次
1. 非線形回帰の概要
2. データの作成
3. モデルの作成(非線形モデル)
4. 正則化法
5. おわりに
1. 非線形回帰の概要
線形回帰とは、説明変数(x)に対して目的変数(y)が線形で表される状態を指します。
モデル式で書くと以下の通りです。
y=w_0+w_1 \cdot x_1+w_2 \cdot x_2+ \cdots +w_i \cdot x_i
ここで、非線形な回帰の具体的な例を考えてみると、
e.g. \qquad y=w_0 + w_1 \cdot x + w_2 \cdot x^2 + w_3 \cdot x^3\\
e.g. \qquad y=w_0 + w_1 \cdot \sin x+w_2 \cdot \cos x + w_3 \cdot \log x
などが挙げられますね。いずれの式もxに対しては明らかに線形ではありません。
ここで、線形回帰のモデル式と非線形回帰の具体例を比べてみると、線形回帰の各x(x1, x2, …)が、非線形回帰では任意のxの関数_Φ_(x)で置き換えられていることが分かると思います。分かりづらいので具体例の1つ目の式で説明すると、
y=w_0 + w_1 \cdot x + w_2 \cdot x^2 + w_3 \cdot x^3\\
\Leftrightarrow \quad y=w_0 + w_1 \cdot \phi_1(x) + w_2 \cdot \phi_2(x) + w_3 \cdot \phi_3(x)\\
\phi(x):xの任意の関数 \quad \phi_1(x) = x, \ \ \phi_2(x) = x^2, \ \ \phi_3(x) = x^3
この_Φ_(x)に多項式関数などの非線形関数を用いると、非線形回帰式が得られます。ここで、このモデルをよく観察すると、xに対しては非線形ですが、重みwに対して線形であるという関係を持っていることが分かりますね。これはつまり、基底関数を用いた非線形回帰の重みwの学習は、線形回帰と同様の計算で求められる、ということです。
(※今後、詳しく説明した記事は書いていきます…)
Φ(x)は基底関数とも呼ばれ、よく使われる基底関数としては、
- 多項式関数
- ガウス型基底関数
などが挙げられます。本記事では、この基底関数に色々な関数を用いた際の非線形回帰モデルを求めていきたいと思います。
2. データの作成
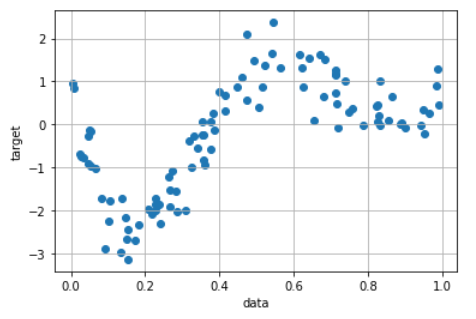
まずはじめに、非線形回帰分析をする非線形データをnumpyを活用して作成していきましょう。
import numpy as np
import matplotlib.pyplot as plt
# データ点数
n = 100
# データを生成する関数の定義(4次関数)
def true_func(x):
z = 1-48*x+218*x**2-315*x**3+145*x**4
return z
# ランダムな点と定義した関数からtargetを生成
data = np.random.rand(n).astype(np.float32)
data = np.sort(data) ## 後に作成するグラフの関係でデータを昇順に並べ替える
target = true_func(data)
# targetにノイズを与える
noise = 0.5 * np.random.randn(n)
target = target + noise
# 作成したデータの可視化
plt.scatter(data, target)
plt.ylabel('target')
plt.xlabel('data')
plt.grid()
plt.show()
3. モデルの作成
3.1. 多項式関数を利用したモデル
早速モデルの作成に移っていきましょう。まずは、イメージの付きやすい多項式関数を利用したいと思います。
多項式関数は以下の通り表されます。
\phi(x) = x^j
scikit-learnで多項式関数に変換するには、sklearn.preprocessing.PolynomialFeaturesを利用します。
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
# データとターゲットをモデルに適した形状に変換する
data = data.reshape(-1,1)
target = target.reshape(-1,1)
# 次数の設定
deg = [1,2,3,4,5,6,7,8,9,10]
# 次数の数だけグラフを準備(2行5列のサブプロット)
fig, axes = plt.subplots(2, 5, figsize=(25,8))
# 非線形変換とパラメータ学習
for d in deg:
# pipelineを活用してデータの変換から学習・推定までの処理を一つの推定器として実行
# 多項式変換した後、線形回帰モデルでパラメータを学習
regr = Pipeline([
('poly', PolynomialFeatures(degree=d)),
('linear', LinearRegression())
])
# モデルの学習
regr.fit(data, target)
# 学習モデルによる予測結果の算出
p_poly = regr.predict(data)
# グラフ作成(次数の数だけグラフ化)
if d < 6:
i, j = 0, d-1
else:
i, j = 1, d-6
axes[i][j].scatter(data, target)
axes[i][j].plot(data, p_poly, color='black') # 決定係数の算出
axes[i][j].set_title('R^2={:.3f}'.format(regr.score(data, target)))
plt.show()
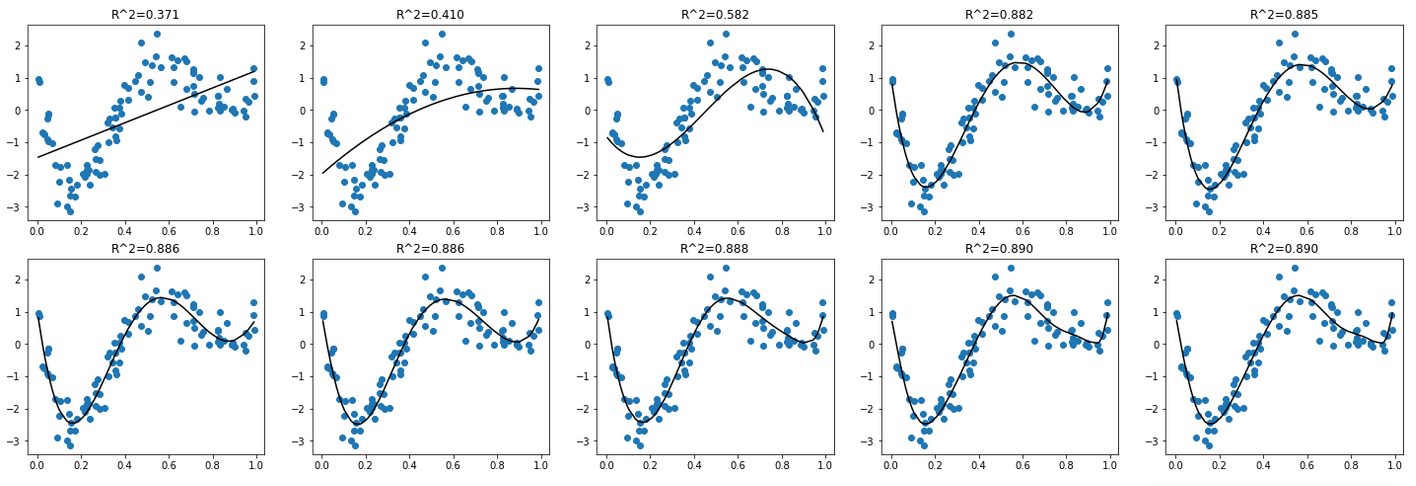
訓練データをプロットとして、学習した回帰モデルを線として併せてグラフ化しています。各グラフは、左上から順に1つずつ次数が大きくなった場合の回帰モデルを描画しており、各グラフの上には決定係数R^2を示しています。
決定係数を見ると、4次以上で決定係数R^2>0.8と比較的高く、グラフのプロットと回帰線が適合していることからも、精度良く予測可能なモデルが得られることが分かります。
※そもそも4次式からデータを作成したので当たり前ですね…
3.2. ガウス型基底関数を利用したモデル
次に、基底関数としてよく使用されるガウス型基底関数を利用したいと思います。
ガウス型基底関数は以下の通り表されます。
k_{rbf} (x_1,x_2) = exp(-\gamma \ ||x-x'||^2)
<参考になる解説記事>
・ガウスカーネル
scikit-learnでガウス型基底関数に非線形変換するには、sklearn.metrics.pairwise.rbf_kernelを利用します。
from sklearn.metrics.pairwise import rbf_kernel
# ガウス型基底関数によるの非線形変換
kx = rbf_kernel(X=data, Y=data, gamma=500)
# 線形回帰によるパラメータ学習
clf = LinearRegression()
clf.fit(kx, target)
# 学習モデルによる予測結果の算出
p_lin = clf.predict(kx)
# グラフ作成
plt.scatter(data, target,label='data')
plt.plot(data, p_lin, color='black', linestyle='-',label='ridge regression')
plt.legend()
plt.grid()
plt.show()
# 決定係数の算出
print(clf.score(kx, target))
> 0.8831058790919062
多項式関数と同様に決定係数R^2は高い一方で、グラフを見ると回帰線が各プロットに追従しており、過学習が生じていることが推察されます。これは、ガウス型基底関数を用いた非線形回帰モデルの表現力が高すぎたことによると考えられます。
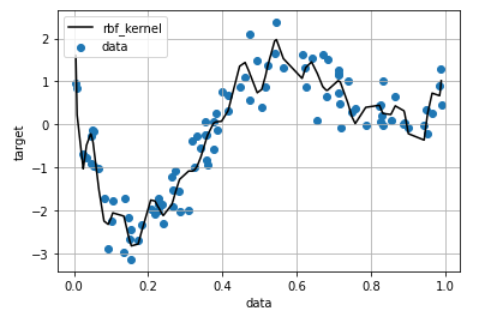
4. 正則化法
先ほどのモデルでは、過学習が起きてしまいました。私たちが欲しいのは訓練データに対する精度ではなく、予測データに対する精度、すなわち汎化性能ですので、望ましい結果とは言えません。そこで過学習を防ぐために用いるのが、正則化(regularization)と呼ばれる手法です。
<参考になる解説記事>
・正則化
4.1 リッジ回帰
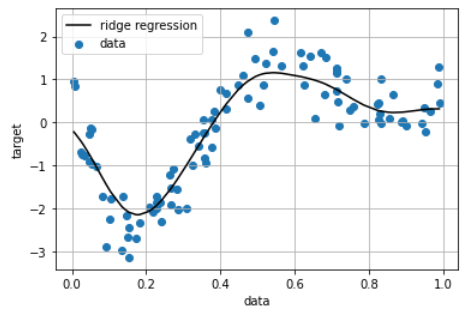
リッジ回帰では重みwのL2ノルムの2乗を加えることで正則化(L2正則化)を行います。
実装は非常に簡単で、リッジ回帰をするにはscikit-learnでsklearn.linear_model.Ridgeを利用します。
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Ridge
kx = rbf_kernel(X=data, Y=data, gamma=100)
clf = Ridge(alpha=30) #リッジ回帰モデル
clf.fit(kx, target)
p_ridge = clf.predict(kx)
plt.scatter(data, target,label='data')
plt.plot(data, p_ridge, color='black', linestyle='-',label='ridge regression')
plt.ylabel('target')
plt.xlabel('data')
plt.legend(loc=2)
plt.grid()
plt.show()
print(clf.score(kx, target))
> 0.8509308250546881
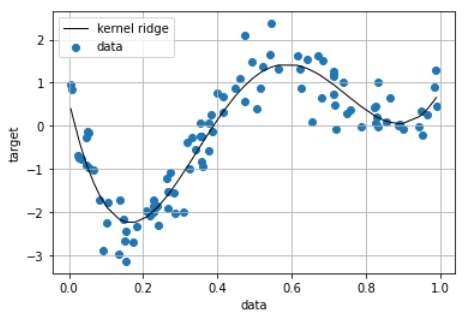
(補足)KernelRidgeによる実装
scikit-learnでは、ガウス型基底関数とRidge回帰を組み合わせたモデルであるKernelRidgeモデル(L2制約付き最小二乗学習)が実装されています。sklearn.kernel_ridge.KernelRidge
from sklearn.kernel_ridge import KernelRidge
clf = KernelRidge(alpha=0.0002, kernel='rbf') #KernelRidge
data = data.reshape(-1,1)
target = target.reshape(-1,1)
clf.fit(data, target)
p_kridge = clf.predict(data)
plt.scatter(data, target, label='data')
plt.plot(data, p_kridge, color='black', linestyle='-', linewidth=1, label='kernel ridge')
plt.ylabel('target')
plt.xlabel('data')
plt.legend()
plt.grid()
plt.show()
print(clf.score(data, target))
> 0.8761027031239897
4.2 ラッソ回帰
ここまでにL2正則化をするリッジ回帰を見てきたが、L1正則化をするラッソ回帰を適用してみましょう。scikit-learnでラッソ回帰をするには、sklearn.linear_model.Lassoを利用します。
L1正則化では、いくつかの係数が完全に0になり、モデルにおいていくつかの特徴量が完全に無視されるということになります。
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Lasso
kx = rbf_kernel(X=data, Y=data, gamma=100) #ラッソ回帰モデル
clf = Lasso(alpha=10000, max_iter=1000)
clf.fit(kx, target)
p_lasso = clf.predict(kx)
plt.scatter(data, target,label='data')
plt.plot(data, p_lasso, color='black', linestyle='-',label='lasso regression')
plt.ylabel('target')
plt.xlabel('data')
plt.legend(loc=2)
plt.grid()
plt.show()
print(clf.score(kx, target))
> 0.0
グラフを見ると、ラッソ回帰では制約の掛け方強すぎて、表現力が失われてしまっていることが分かります。
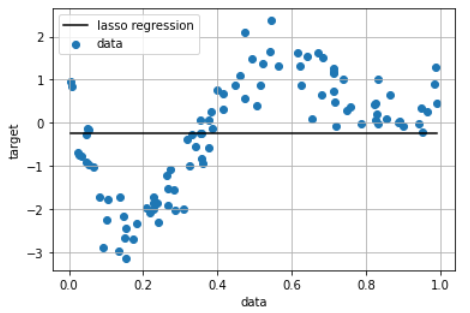
4.3 サポートベクター回帰(SVR)
サポートベクターマシン(SVM)を回帰分析に応用したサポートベクター回帰(SVR)を利用してみます。
<参考になる解説記事>
・サポートベクター回帰
from sklearn import model_selection, preprocessing, linear_model, svm
clf = svm.SVR(kernel='rbf', C=1e3, gamma=0.1, epsilon=0.1) # サポートベクター回帰, カーネル:ガウス型基底関数
clf.fit(data, target)
p_rbf = clf.fit(data, target).predict(data)
plt.scatter(data, target, label='data')
plt.plot(data, p_rbf, color='black', label='Support Vector Regression (RBF)')
plt.legend()
plt.show()
print(clf.score(data, target))
> 0.39919066878220344
結果が得られましたが、グラフ、決定係数からもそれほど当てはまりが良くないことが分かります。ハイパーパラメータの設計が必要そうです。
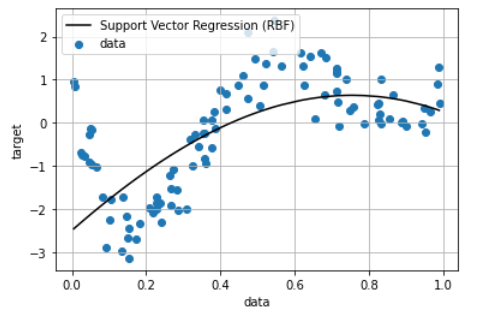
5. おわりに
本記事では、非線形回帰を活用して回帰問題を解きました。基底関数に、多項式関数、ガウス型基底関数を利用してデータを非線形変換し、回帰モデルでパラメータ学習することでモデルが得られました。モデルの表現力が高すぎると過学習が生じるため、正則化(L2正則化:Ridge、L1正則化:Lasso)を活用して適切な表現力を持つモデルを作成しました。
実装に焦点を当てたので、今後は数学的背景などの解説記事を書いていきたいと思います。
機械学習入門のリンク
今後も引き続き機械学習の実装入門を記事にしていきます。
参考にどうぞ。
・線形回帰モデル
・非線形回帰モデル 本記事
・k-近傍法
・ロジスティック回帰モデル
・主成分分析
・K-means
・サポートベクターマシン ※今後更新予定