線形な手法とカーネル法（回帰分析）

まえがき

線形な手法とはなんぞや。カーネル法とはなんぞや。機械学習について学んだことがある人なら言葉くらいは聞いたことがあるかもしれません。

線形な手法とは、ざっくり言えば一次の連立方程式を解くだけで答えが求まるように問題を設計することです。つまり逆行列さえ計算できれば問題が解けるということなので、とても簡単です。

ただ、線形な手法で解ける問題は限られています。たとえばグラフ上の点を直線で近似するようなことしかできません。けれど世の中そんなまっすぐじゃないですよね。もっとクネクネしたい。クネクネしているのを「非線形」といいますが、非線形な手法は解くのが非常に難しい場合が多いです。

そこで用いるのがカーネル法です。カーネル法は生データに非線形写像を施してやって、それを新しいデータとみなして線形な手法を適用してやることで問題を解きます。つまり「生データをクネクネした空間にうまいこと並べ直してあげれば、その空間の中ではスパッと一直線になってるんじゃないの？」というのがカーネル法の発想です。そしてクネクネした空間で引いた直線を、私たちの住むまっすぐな空間に持ってきてあげたら、きっとクネクネになっていますよね。やったぜ、ほとんど線形な手法を使ってクネクネできた！

カーネル法を使うと、線形な手法で培ってきた知識をほとんどそのまま生かして非線形なデータを扱うことができます。また、カーネル法はいま流行りの深層学習やニューラルネットワークに比べて数学的に整備されており、なぜ上手くいくのかといった点にブラックボックスがありません。

今回は線形回帰と多重線形回帰についてじっくり解説したあと、カーネル回帰へと話を展開します。

注意

この記事では列ベクトルを${\bf x}$と表記し、行ベクトルは${\bf x}^{\mathrm{T}}$のように転置記号を用いて表記します。

今回用いるサンプルコードはこちらです。Google Colaboratory にアップロードしてあるので、Googleアカウントをお持ちであれば実行できるかと思います。

2020/11/28追記

当記事のコメント欄で議論した、より理論的な側面に踏み込んだ内容を整理した記事を公開しました。

カーネルリッジ回帰

線形回帰

ものすごい今さら感がありますが、まずは線形回帰について解説します。

そもそも回帰ってなんぞや。統計とか機械学習の分野で回帰と言ったら回帰分析のことを指します。回帰分析とは、実際に観測されたデータの分布を見て、それを再現するような関数を探し出してあげよう、という方法です。回帰分析によって関数を見つけてあげれば、実際に観測していないデータについてもどんな値を取るか予測できるようになります。データを直線に回帰する場合、これを線形回帰といいます。

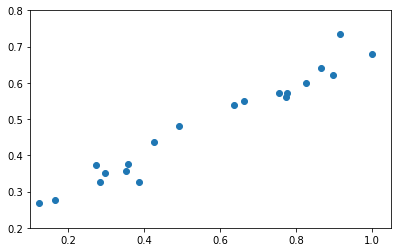
どういうものかは実際に見たほうが早いです。下のように、いかにも直線っぽいデータが観測されたとします。

たとえば縦軸を電圧$V$、横軸を電流$I$として物質の電気抵抗$R$を測ろうとしたらこういうグラフが出てきますよね。理論的には$V=RI$なので綺麗に直線になっていてほしいのですが、電気抵抗に限らず実際のデータはなんかよくわからない理由によってゆらぎます。ここから先は議論を一般化するため、縦軸を$y$、横軸を$x$として直線$\hat{y}=f(x)=w_0 + w_1x$の切片$w_0$と傾き$w_1$を求めよ、ということにします（回帰した結果としての出力にはハット記号をつけて$\hat{y}$のように表記し、実際に観測された値$y$と区別することが多いです）。

私たちは$N$個のデータを観測したとします。すなわち$x$に対応した$y$の値のデータの組を、

(x^{(1)}, y^{(1)}), (x^{(2)},y^{(2)}), \ldots, (x^{(N)},y^{(N)})

のように集めてきました。観測されたデータに含まれるゆらぎを考慮しつつも、それっぽい直線を引きたい。じゃあどんな直線が一番それっぽいの？ということを表すために誤差関数$R({\bf w})$というものを定義します（念のため、抵抗$R$とはまったく関係ないです）。

誤差関数$R$の選び方にはいろいろあるのですが、とりあえず二乗誤差$r_{square}$（残差平方和$RSS$ともいいます）を用いることを考えて見ましょう。二乗誤差とは、実際に観測されたデータと回帰直線によって予測された値との差の2乗を取って、それをすべての点について総和したものであり、$w_0$と$w_1$の関数です（${\bf w}=(w_0, w_1)^{\mathrm{T}}$とおけば、$R$はベクトル${\bf w}$の関数です）。

R({\bf w}) = r_{square}(w_0,w_1)= \sum_{i=1}^{N}\left\{y^{(i)}- f(x^{(i)})\right\}^2
= \sum_{i=1}^{N}\left\{y^{(i)}- (w_0 + w_1 x^{(i)})\right\}^2

つまりこの誤差関数$R({\bf w})$を最小化する${\bf w}$を見つけてやれば、二乗誤差という尺度のもとでもっともそれっぽい直線を引けるというわけです。見つけ方は簡単です。$R({\bf w})$は$w_1,w_2$に関する二次式になっているので、偏微分して$0$になる場所が極値になります（$R({\bf w})$は0以上の範囲にある二次関数なので、極値で最小となります）。ここで、

{\bf y} = 
\left(\begin{matrix}
y^{(1)} \\
y^{(2)} \\
\vdots \\
y^{(N)}
\end{matrix}\right)
,\;
X=
\left(\begin{matrix}
1 & x^{(1)} \\
1 & x^{(2)} \\
\vdots & \vdots\\
1 & x^{(N)}
\end{matrix}\right)

とおくと、実は誤差関数は

R({\bf w}) = ({\bf y} - X{\bf w})^{\mathrm{T}} ({\bf y} - X{\bf w})

と表すことができます（本当にそうなるか、一度確かめてみると面白いです）。合成関数の微分を用いれば、

\begin{align}
\frac{\partial R({\bf w})}{\partial {\bf w}} &=
\left(\begin{matrix}
\frac{\partial R({\bf w})}{\partial w_0} \\
\frac{\partial R({\bf w})}{\partial w_1} 
\end{matrix}\right)
=
\left(\begin{matrix}
 - 2\sum_{i=1}^{N}1 \cdot \left\{y^{(i)}-(w_0+w_1x^{(i)})\right\} \\
 - 2\sum_{i=1}^{N}x^{(i)}\left\{y^{(i)}-(w_0+w_1x^{(i)})\right\}
\end{matrix}\right)\\
&= -2X^{\mathrm{T}}({\bf y} - X{\bf w}) ={\bf 0}
\end{align}

となりますので、これを解いて

\begin{align}
-2X^{\mathrm{T}}({\bf y} - X{\bf w}) ={\bf 0} \\
\therefore {\bf w} =(X^{\mathrm{T}}X)^{-1}X^{\mathrm{T}}{\bf y}
\end{align}

となります（ただし$X^{\mathrm{T}}X$に逆行列が存在するときに限ります）。

では実際にやってみましょう。実は、さっき図に示したいかにも直線っぽいデータはガウス分布にしたがった人工的なバラつきを与えて直線の周囲に生成したデータです。

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns

# 線形回帰モデル用データセット
# a : slope of a line
# b : intercept of a line
# size : number of data
# xlim : domain of variable x
# scale : standard deviation
def linear_dataset(a, b, size, xlim=[0, 1], scale=None):
    x = np.random.uniform(xlim[0], xlim[1], size)
    y = a * x + b
    if scale is not None:
        noize = np.random.normal(0, scale, size)
        y = y + noize
    df = pd.DataFrame()
    df['x'] = x
    df['y'] = y
    return df

# データを生成
data = linear_dataset(0.5, 0.2, 20, scale=0.03)

# データを描画
plt.figure(figsize=(6.472, 4))
plt.scatter(data['x'].values, data['y'].values)
plt.xlim((0.1, 1.05))
plt.ylim((0.2, 0.8))
plt.show()

傾きは0.5,切片は0.2に設定してあります。上のコードを実行すると大体同じようなデータセットが生成されると思います。そしてこれを線形回帰にかけます。

def linear_regression(X, Y):
    X = np.stack((np.ones(X.shape[0]), X), axis=1)
    W = (np.linalg.inv(X.T.dot(X)).dot(X.T)).dot(Y)
    return W

# 重みWを求める
W = linear_regression(data['x'].values, data['y'].values)

こうして求めたWを print(W) などを用いて表示すると求めた重みを直接覗くことができます。私が実行したときは [ 0.19135655 0.50836672] となりました。元々が切片0.2,傾き0.5の直線から生成したデータであることを考えれば、うまくいってますね。実際はこんな出来レースみたいな評価はよろしくないので、求めた直線を元のグラフに描画して確かめます。

X = np.arange(0, 1.5, 0.01)
Y = W[0] + W[1] * X

plt.figure(figsize=(6.472, 4))
plt.scatter(data['x'].values, data['y'].values)
plt.plot(X, Y)
plt.xlim((0.1, 1.05))
plt.ylim((0.2, 0.8))
plt.show()

多重線形回帰

先ほどは入力$x$と出力$y$がいずれも1次元の場合を扱っていたので、直線$\hat{y}=w_0 + w_1x$に回帰させていました。入力がより高次元の${\bf x}=(x_1,x_2,\ldots,x_n)^{\mathrm{T}}$のn次元の入力に一般化された線形回帰を多重線形回帰といい、次の式で表します。

\hat{y} = f({\bf x}) = w_0 + w_1 x_1 + w_2 x_2 + \ldots + w_n x_n 

この式は行列を用いて

\hat{y} =
\left(\begin{matrix}
1 & x_1 & x_2 & \cdots & x_n
\end{matrix}\right)
\left(\begin{matrix}
w_0 \\
w_1 \\
w_2 \\
\vdots \\
w_n
\end{matrix}\right)

と書き直すことができます。さらに出力が${\bf y} =(y_1,y_2,\ldots,y_m)^{\mathrm{T}}$の$m$次元の場合にも

Y = 
\left(\begin{matrix}
y_1^{(1)} & y_2^{(1)} & \cdots & y_m^{(1)} \\
y_1^{(2)} & y_2^{(2)} & & \vdots \\
\vdots & & \ddots & \vdots\\
y_1^{(N)} & \cdots & \cdots & y_m^{(N)}
\end{matrix}\right)
,\;
X =
\left(\begin{matrix}
1 & x_1^{(1)} & x_2^{(1)} & \cdots & x_n^{(1)}\\
1 & x_1^{(2)} & x_2^{(2)} & & \vdots\\
\vdots & & & \ddots&\vdots\\
1 & x_1^{(N)} & \cdots & \cdots & x_n^{(N)}
\end{matrix}\right)

W =
\left(\begin{matrix}
w_{10} & w_{20} & \cdots & w_{m0} \\
w_{11} & w_{21} & & \vdots \\
\vdots & & \ddots & \vdots\\
w_{1n} & \cdots & \cdots & w_{mn}
\end{matrix}\right)

のように定義することで、

\hat{Y} = f(X)=XW \\
R(W) = (Y-XW)^{\mathrm{T}} (Y-XW) \\
\therefore W = (X^{\mathrm{T}}X)^{-1}X^{\mathrm{T}} Y

として、一次元の場合と同様に解くことができます。

カーネル回帰

ちょっとだけ多重線形回帰を思い出してみましょう。多重線形回帰は$x_0=1$とおけば以下の式で表すことができるのでした（$\Sigma$を用いて書き直してあります）。

f({\bf x}) = \sum_{i=0}^{n} w_i x_i

カーネル回帰では以下のような式で関数を近似します。

f({\bf x}) = \sum_{i=1}^{N} \alpha_i k({\bf x}^{(i)}, {\bf x})

多重線形回帰によく似た式になっていますね。$k({\bf x}, {\bf x}')$はカーネル関数と呼ばれるもので、一定の条件さえ満たせば自由に設計することができます（この辺りを詳しく知りたい人は参考文献[1]をご覧ください）。今回はよく使われるガウスカーネルを用います。ガウスカーネルは次のように定義されます。

k({\bf x}, {\bf x}') = exp(-\beta \|{\bf x} - {\bf x}'\|^2)

ただし$\|{\bf x} - {\bf x}'\|=\sqrt{\sum_{j=1}^n (x_j - x'_j)^2}$はベクトル同士の距離（$L^2$ノルム）を表しています。$\beta$は$\beta \gt 0$を満たす実数のハイパーパラメータであり、使う人が勝手に決めます（結果を見ながらいろいろいじくってみるのが普通です）。

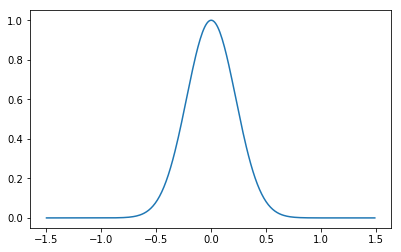
もう少しカーネル回帰の式を詳しく考察してみましょう。入力が1次元の場合、ガウスカーネルは$k(x,x')=exp(-\beta(x-x')^2)$と書き直すことができます。$x'=0$とおいて$x$を動かしてガウスカーネルをプロットすると、下の図のようになります。

def kernel(xi, xj, beta=1):
    return np.exp(- beta * np.sum((xi - xj)**2))

X = np.arange(-1.5, 1.5, 0.01)
Y = np.zeros(len(X))
for i in range(len(X)):
    Y[i] = kernel(X[i], 0, 10)

plt.figure(figsize=(6.472, 4))
plt.plot(X, Y)
plt.show()

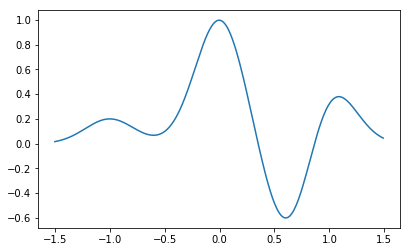
$x'$に値を入れると、このガウスカーネルは左右に動きます。実際は観測されたデータの数だけ$x'$に値を代入して、その$N$個のガウスカーネルを線形に足し合わせたものがカーネル回帰になります。ガウスカーネルを5個くらい適当にズラしつつ適当に重みづけて足し合わせたのが下の図です。

def kernel(xi, xj, beta=1):
    return np.exp(- beta * np.sum((xi - xj)**2))

X = np.arange(-1.5, 1.5, 0.01)
Y = np.zeros(len(X))

centers = [-1, 0, 0.5, 0.6, 1]
weights = [0.2, 1, 0.3, -1, 0.5]
for i in range(len(X)):
    for weight, center in zip(weights, centers):
        Y[i] += weight * kernel(X[i], center, 10)

plt.figure(figsize=(6.472, 4))
plt.plot(X, Y)
plt.show()

これ、うまいこと足し合わせればどんな関数でも近似できそうですよね（実際、無限個のガウス関数の足し合わせで、任意の非線形関数を任意の精度で近似することができます）。このうまい足し合わせ方を見つけてやるのがカーネル回帰です。

カーネル回帰の式はやはりベクトルを使って次のように書くことができます。

\hat{y} =
\left(\begin{matrix}
k({\bf x}^{(1)}, {\bf x}) & k({\bf x}^{(2)}, {\bf x}) & \cdots & k({\bf x}^{(N)}, {\bf x})
\end{matrix}\right)
\left(\begin{matrix}
\alpha_0 \\
\alpha_1 \\
\vdots \\
\alpha_N
\end{matrix}\right)

ここまで来れば、なぜ線形回帰についてしつこく丁寧に解説してきたか、察しがつくかと思います。

{\bf y} = 
\left(\begin{matrix}
y^{(1)} \\
y^{(2)} \\
\vdots \\
y^{(N)}
\end{matrix}\right)
,\;
K=\left(\begin{matrix}
k({\bf x}^{(1)}, {\bf x}^{(1)}) & k({\bf x}^{(2)}, {\bf x}^{(1)}) & \cdots & k({\bf x}^{(N)}, {\bf x}^{(1)}) \\
k({\bf x}^{(1)}, {\bf x}^{(2)}) & k({\bf x}^{(2)}, {\bf x}^{(2)}) & & \vdots \\
\vdots & & \ddots & \vdots \\
k({\bf x}^{(1)}, {\bf x}^{(N)}) & \cdots & \cdots & k({\bf x}^{(N)}, {\bf x}^{(N)})
\end{matrix}\right) 
,\;
{\bf \alpha}
=
\left(\begin{matrix}
\alpha^{(1)} \\
\alpha^{(2)} \\
\vdots \\
\alpha^{(N)}
\end{matrix}\right)

とおきます（この$K$はグラム行列と呼ばれています）。グラム行列を用いるとカーネル回帰による二乗誤差$R({\bf \alpha})$は

\begin{align}
R({\bf \alpha}) &= r_{square}({\bf \alpha})= \sum_{i=1}^{N}\left\{y^{(i)}- f({\bf x}^{(i)})\right\}^2
=\sum_{i=1}^{N}\left\{y^{(i)}- \sum_{i=1}^{N} \alpha_i k({\bf x}^{(i)}, {\bf x})\right\}^2 \\
&=({\bf y}- K {\bf \alpha})^{\mathrm{T}}({\bf y}- K {\bf \alpha})
\end{align}

と表すことができ、したがって

{\bf \alpha} = (K^{\mathrm{T}}K)^{-1}K^{\mathrm{T}}{\bf y} = K^{-1}{\bf y}

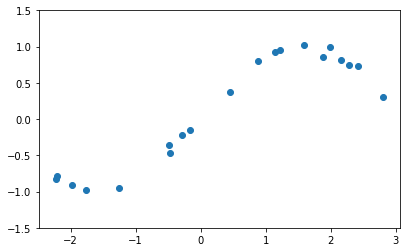
と解くことができます。線形回帰はせいぜい直線とかまっすぐな平面でしか近似することができませんでした。つまり次のようなデータセットに対して線形回帰を用いてもうまくいかないことはすぐに分かります。

# カーネル回帰モデル用データセット
# size : number of data
# xlim : domain of variable x
# scale : standard deviation
def wave_dataset(size, xlim=[0, 1], scale=None):
    x = np.random.uniform(xlim[0], xlim[1], size)
    y = np.sin(x)
    if scale is not None:
        noize = np.random.normal(0, scale, size)
        y = y + noize
    df = pd.DataFrame()
    df['x'] = x
    df['y'] = y
    return df

# データを生成
data = wave_dataset(20, xlim=[-3.14, 3.14], scale=0.05)

# データを描画
plt.figure(figsize=(6.472, 4))
plt.scatter(data['x'].values, data['y'].values)
plt.ylim((-1.5, 1.5))
plt.show()

実際に線形回帰してみたらどうなるかはご自身で試してみてください。sin関数を使って生成したデータであり、直線ではないのできっとうまくいかないでしょう。

カーネル法で回帰を行うためにはまずグラム行列を計算します（グラム行列は愚直に各成分ごとに計算するしかなく、どうあがいても$O(N^2)$の計算量を要するので、大規模なデータ分析にカーネル法を用いる場合はここがネックのひとつになります）。

from itertools import combinations_with_replacement

X = data['x'].values
Y = data['y'].values

# ハイパーパラメータ
beta = 1

# データ数
N = X.shape[0]

# グラム行列の計算
K = np.zeros((N, N))
for i, j in combinations_with_replacement(range(N), 2):
    K[i][j] = kernel(X[i], X[j])
    K[j][i] = K[i][j]

あとはこれの逆行列に${\bf y}$をかけてやれば重み${\bf \alpha}$が求まるのでした。

# 重みを計算
alpha = np.linalg.inv(K).dot(Y)

あとは最初のほうで示した次の式にこの${\bf \alpha}$を代入してやれば、関数を近似することができるはずです。

f({\bf x}) = \sum_{i=1}^{N} \alpha_i k({\bf x}^{(i)}, {\bf x})

それではこの${\bf \alpha}$を用いていざ近似！

# カーネル回帰
def kernel_predict(X, x, alpha, beta):
    Y = 0
    for i in range(len(X)):
        Y += alpha[i] * kernel(X[i], x, beta)
    return Y

# 回帰によって結果を予測        
X_axis = np.arange(-3.14, 3.14, 0.01)
Y_predict = np.zeros(len(X_axis))
for i in range(len(X_axis)):
    Y_predict[i] = kernel_predict(X, X_axis[i], alpha, beta)

# 結果を描画
plt.figure(figsize=(6.472, 4))

## 観測データ
plt.scatter(data['x'].values, data['y'].values)
## 真の関数
plt.plot(X_axis, np.sin(X_axis), c='red')
## 予測した関数
plt.plot(X_axis, Y_predict)

plt.ylim((-1.5, 1.5))
plt.show()

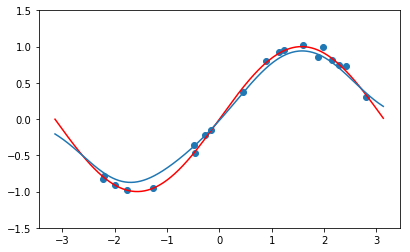
あれれ？全然ダメですね。見つけ出してほしい関数である赤い曲線とは似ても似つかない曲線が描画されています。実はカーネル回帰は表現力が高すぎてそのまま使うと過学習してしまいます（データに含まれるノイズにも正確に合わせようとしてめちゃくちゃになります）。なんでこんなことが起こるかといえば、私たちは${\bf \alpha}$の大きさについてなんの制約も設けなかったからです。${\bf \alpha}$がどんな値を取っているのか、各要素の絶対値の平均を取って見てみましょう。

print(np.mean(np.abs(alpha)))

私が実行したときは45943294574.645447と表示されました。$10^{10}$のオーダーであり非常に大きな値です。ガウスカーネルは$(0, 1]$の値域を持つ関数なので、こんな非常識な大きさの重みをかけて足し合わせようものなら予測した値は宇宙の彼方までぶっ飛んでいきます。sin関数の値域が$[-1,1]$なので重みはせいぜい$1$とか$-1$とかそういう小さい値を取ってほしいはずなのです。

そこで用いるのが正則化 （regularization）と呼ばれる手法です。二乗誤差に正則化項と呼ばれる項を付け加えて最適化します。

\begin{align}
R({\bf \alpha})
&=({\bf y}- K {\bf \alpha})^{\mathrm{T}}({\bf y}- K {\bf \alpha}) + \lambda {\bf \alpha}^{\mathrm{T}} K {\bf \alpha}
\end{align}

このように通常の残差平方和に$\lambda {\bf \alpha}^{\mathrm{T}} K {\bf \alpha}$という項を付け加えて最小化を行うことをリッジ回帰といいます。$\lambda {\bf \alpha}^{\mathrm{T}} K {\bf \alpha}$はリッジ回帰の正則化項といい、実数$\lambda$はハイパーパラメータで、人間が勝手に決めます。

いきなり$\lambda {\bf \alpha}^{\mathrm{T}} K {\bf \alpha}$と言われてもイメージがつかみにくいかもしれませんが、$K{\bf \alpha}$という値は、学習に用いたデータセットについての予測値を列ベクトルとして並べたものであることを思い出せば、${\bf \alpha}^{\mathrm{T}} K {\bf \alpha}$とは、この学習器における予測値にさらに重み${\bf \alpha}$をかけて足し合わせたものです。${\bf \alpha}$が大きくなれば${\bf \alpha}^{\mathrm{T}} K {\bf \alpha}$も大きくなることがわかります。つまり${\bf \alpha}^{\mathrm{T}} K {\bf \alpha}$を最小化することは、${\bf \alpha}$を小さく抑えようという意味があるのです。

$R({\bf \alpha})$は$\lambda = 0$であれば$r_{square}({\bf \alpha})$に一致し、$\lambda$が大きくなるほど${\bf \alpha}^{\mathrm{T}} K {\bf \alpha}$の項が支配的になります。$\lambda$を大きくするほど${\bf \alpha}$は小さい値しか取ることができなくなる、つまり${\bf \alpha}$は限られた範囲の値しか取れなくなるので、学習器の表現力を落とすことになります。もともとの表現力が高すぎたのでこれでいいのです。

正則化項が加わってもやることは変わりません。${\bf \alpha}^{\mathrm{T}} K {\bf \alpha}$は二次形式で、$K$は半正定値であることが証明できる（文献[1]を参照のこと）ので、微分して$0$になったところが最小です。

\begin{align}
\frac{\partial R({\bf \alpha})}{\partial {\bf \alpha}} 
&= -2K^{\mathrm{T}}({\bf y} - K{\bf \alpha}) +2\lambda K {\bf \alpha}={\bf 0}
\end{align}

グラム行列が実対称行列$K=K^{\mathrm{T}}$であることを利用すれば、

{\bf \alpha} = (K+\lambda I_N)^{-1}{\bf y}

となります。$I_N$は$N \times N$の単位行列です。こうして求めた$\alpha$を用いて近似すると、下のようになります。

# 正則化項の係数
lam = 0.5
alpha_r = np.linalg.inv(K + lam * np.eye(K.shape[0])).dot(Y)

# 回帰によって結果を予測
Y_predict_r = np.zeros(len(X_axis))
for i in range(len(X_axis)):
    Y_predict_r[i] = kernel_predict(X, X_axis[i], alpha_r, beta)

# 結果を描画
plt.figure(figsize=(6.472, 4))

## 観測データ
plt.scatter(data['x'].values, data['y'].values)
## 真の関数
plt.plot(X_axis, np.sin(X_axis), c='red')
## 予測した関数
plt.plot(X_axis, Y_predict_r)

plt.ylim((-1.5, 1.5))
plt.show()

今度はうまくいきましたね。${\bf \alpha}$の値をprint(np.mean(np.abs(alpha_r)))で覗いてみると0.14025541758683496となっており、正則化がうまく機能したことがわかります。

多重線形回帰のときのように${\bf \alpha}$をベクトルから行列に拡張することで、出力が高次元の場合にも適用できます。

まとめ

さて、今回はカーネル法の力を用いてクネクネした関数を近似する方法を解説しました。実際にカーネル法の力はすごいのですが、観測したデータ数$N$に対してグラム行列の計算が$O(N^2)$のオーダーになるので、実用を考えるとビッグデータの分析にはあまり向いていません。実務でカーネル法を試すこともあるのですが、感想としては、大規模なデータだとやはり逆行列の計算に恐ろしいくらい時間がかかります。逆行列は要素数$n$に対して$O(n^3)$の計算量を持っていますし、メモリも食います。また、グラム行列はすべての要素が(0,1]の区間にあるため、グラム行列の次元が大きくなると行列式の定義より$det(K) \to 0$となるのでそもそも逆行列がコンピュータでは計算できないというケースすらあります。こういう場合には線形代数やスパースモデリングの知識を駆使しても結果が出るか出ないかって感じなので、データをとりあえず突っ込んでおけばそれっぽい結果が出るニューラルネットワークに押されてるのも仕方ないかなと思います。

それでもデータ数が少ないときとか、中規模のデータくらい（1000件くらい？）までならカーネル法は十分使えます。ニューラルネットワークは基本的にデータをたくさん（1万件とか10万件）持ってこないと学習がうまくいかないことが多いので、住み分けができているのではと思います。

以上でカーネル法を用いた回帰分析の話を終わります。~~続きは書くかもしれないし書かないかもしれません。気長にお待ちください。~~今回で打ち切ることにしました（2020/3/17追記）。お疲れさまでした。

【2019/11/14 追記】
現在は「乱択化フーリエ特徴関数」という手法で大規模データに対しても線形のオーダーで適用可能になっているようです。

『乱択化フーリエ特徴を用いたリッジ回帰』(@hiroponX 様)

【2022/4/16追記】
続きではないですが、もっと理論的にきっちり学びたいという人のために書籍を書きました。

参考

[1]カーネル多変量解析
[2]統計的学習の基礎
[3]https://www.slideshare.net/ShinyaShimizu/ss-11623505