本記事の概要
scikit-learnの乳がん検査のデータセット(Breast Cancer)を分析しましょう。
本記事では教師なし学習の機械学習手法で次元圧縮に利用される主成分分析(PCA:principal component analysis)を実践的に学びます。
「機械学習を触ってみたいけど、データもないからどこから手を付けていいか分からない。」
そんな方にも機械学習の入門としておすすめです。
目次
1. 主成分分析の概要
2. データセットの確認
3. 主成分分析(PCA)
4. おわりに
1. 主成分分析の概要
主成分分析とは、多数のデータの持つ構造を、重要な一部の指標(変数)に次元を削減する分析手法です。次元削減では、特徴量を相互に統計的に関連しないように回転させ、情報の損失を小さくしています。次元削減をすることで少数の重要な変数を利用した分析や可視化が出来ます。
<参考になる解説記事>
・主成分分析
2. データセットの確認
まずは、今回分析の対象とする乳がんデータセットを確認してみましょう。scikit-learnのsklearn.datasets.load_breast_cancerを利用します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
%matplotlib inline
data_breast_cancer = load_breast_cancer()
# Pandasによるデータの表示
df_target = pd.DataFrame(data_breast_cancer["target"], columns=["target"])
df_data = pd.DataFrame(data_breast_cancer["data"], columns=data_breast_cancer["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
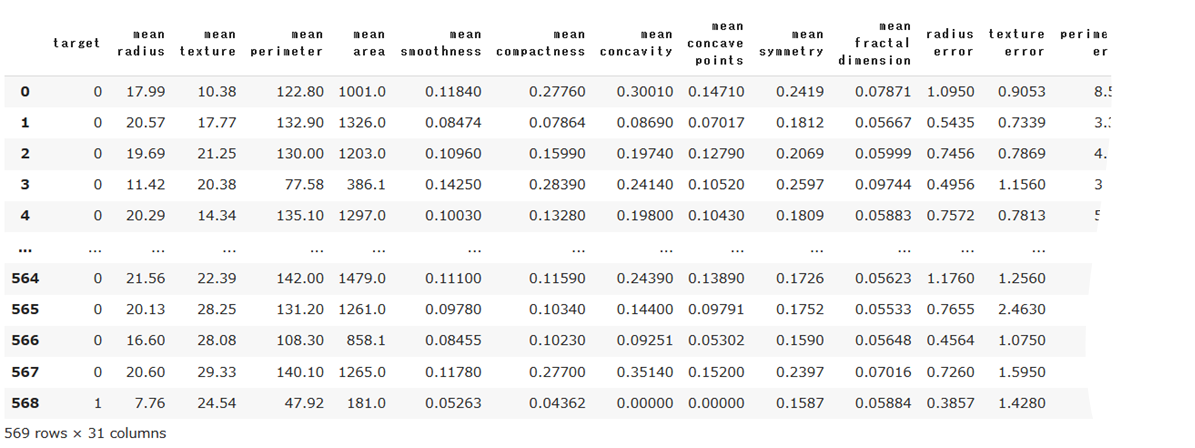
df
目的変数(target)を除いて、説明変数が30個、データが569個あります。targetの0と1はそれぞれ以下の通りです。
print(data_breast_cancer.target_names)
> ['malignant' 'benign']
# 0 = malignant:悪性、1 = benign:良性
表だけだと理解出来ないので、malignant(悪性)とbenign(良性)を色分けしてデータを可視化してみましょう。
fig, axes = plt.subplots(10, 3, figsize=(10,20))
# targetによるデータフレームのソート
malignant = df[df["target"] == 0]
benign = df[df["target"] == 1]
ax = axes.ravel()
# 説明変数1~30のグラフ作成、dfはtargetと結合しているためインデックスに注意
for i in range(30):
_, bins = np.histogram(df.iloc[:,i+1], bins=50)
ax[i].hist(malignant.iloc[:,i+1].values, bins=bins, alpha=0.5)
ax[i].hist(benign.iloc[:,i+1].values, bins=bins, alpha=0.5)
ax[i].set_title(df.columns[i+1])
ax[i].set_yticks(())
ax[0].set_xlabel("Feature magnitude")
ax[0].set_ylabel("Frequency")
ax[0].legend(["malignant", "benign"], loc="best")
fig.tight_layout()
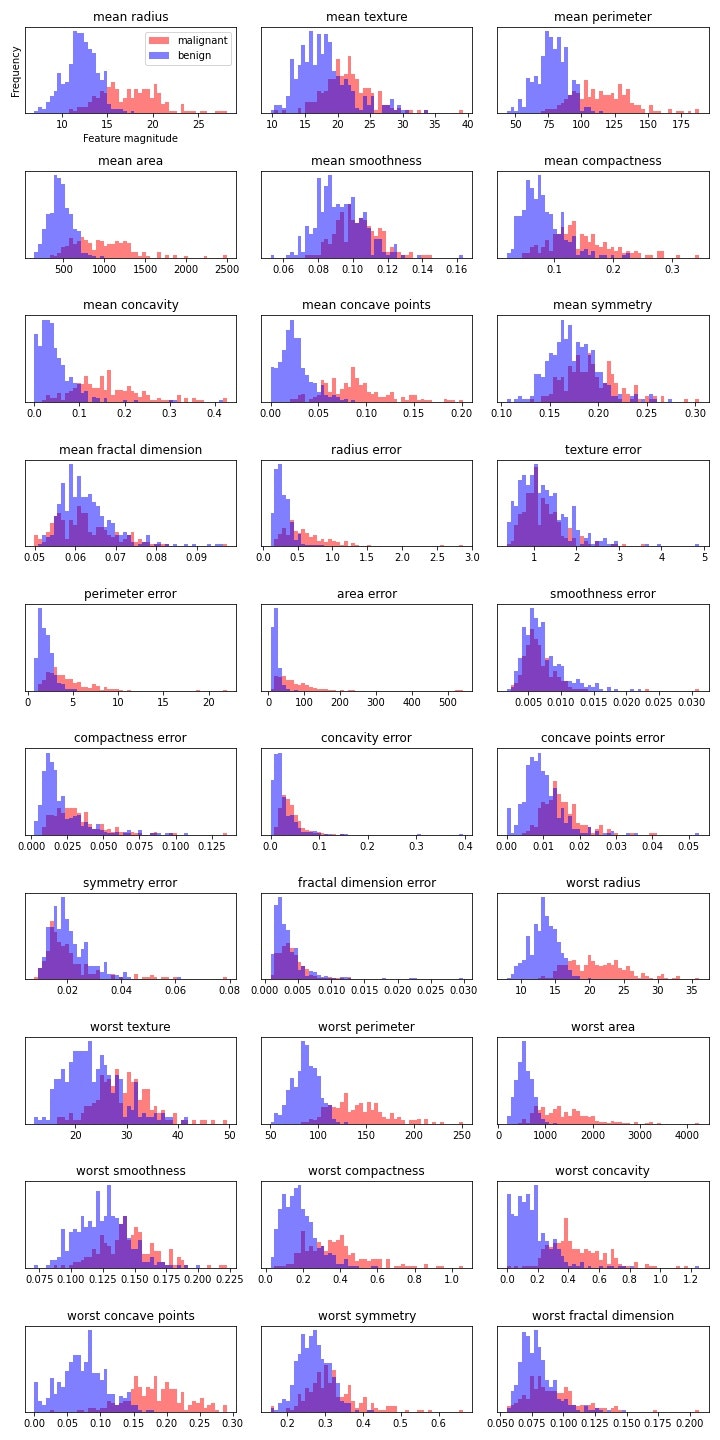
以下のようなヒストグラムが得られました。このデータから、mean radiusやworst concave pointsなどの説明変数の重なりが少ないため、malignant(悪性, 赤色)とbenign(良性, 青色)を分類するのに役に立ちそうです。
3. 主成分分析(PCA)
乳がんデータセットの説明変数を確認すると、malignant(悪性)とbenign(良性)をなんとなく分類できそうなことが分かりました。ただ、説明変数が30個もあるので、個々の変数の相関や分類に与える影響については理解できません。
そこで、主成分分析(PCA)を用いて人が相関を確認できる2次元まで次元を削減できれば、主な相関を捉えることができるので全体像が見やすくなります。それでは、主成分分析で解析を進めてみましょう。scikit-learnで、主成分分析を実装するには、sklearn.decomposition.PCAを利用します。
3.1. データの前処理
まずはじめにデータの前処理をしていきます。
個々の特徴量を平均が0で分散が1になるように変換します。
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 目的変数の抽出
y = df["target"]
# 説明変数の抽出
X = df.loc[:, "mean radius":]
# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
X_train.shape
> (426, 30)
# 標準化
scaler = StandardScaler()
# fit_transform 統計情報を計算して正規化を実行する
X_train_scaled = scaler.fit_transform(X_train)
# テストデータの変換には訓練データで計算された最小・最大値を使用
X_test_scaled = scaler.transform(X_test)
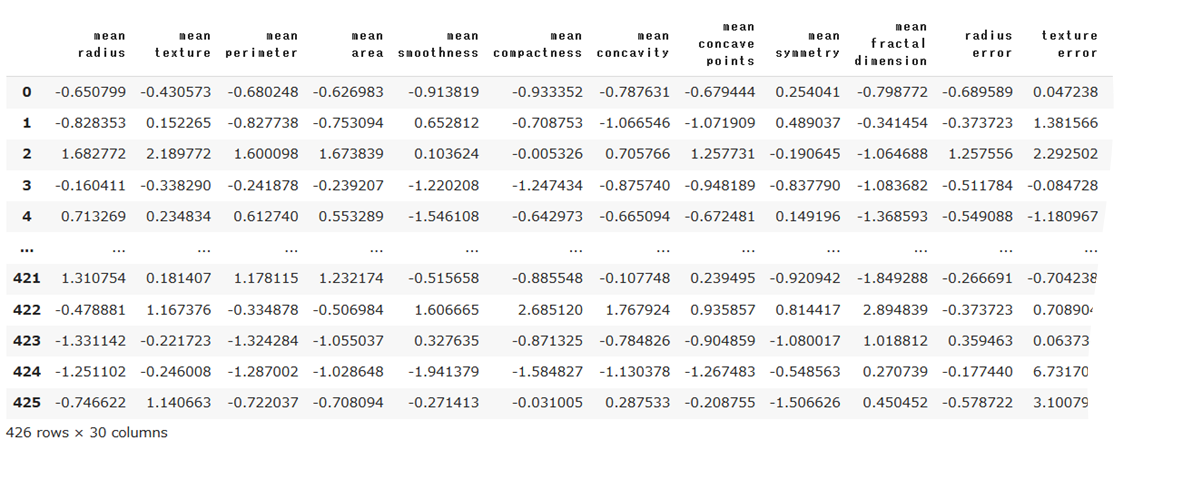
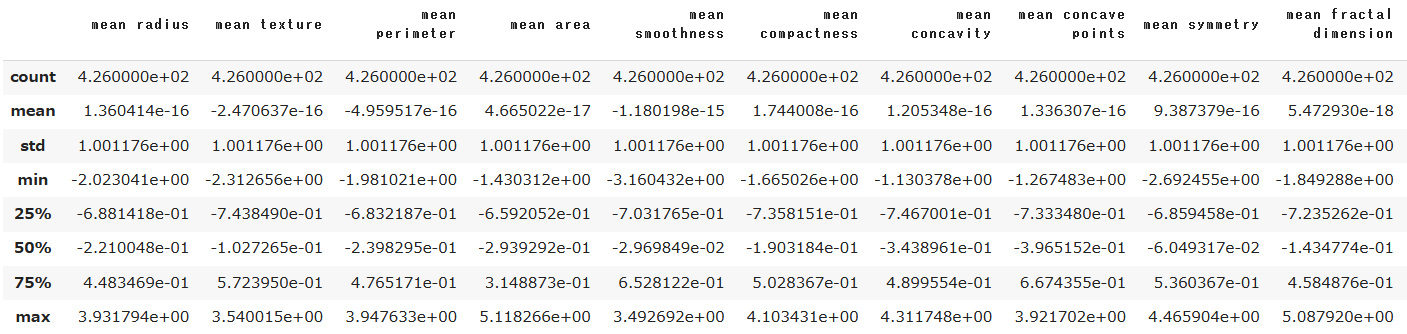
要約統計量を確認してみます。
df_scaled.describe()
いずれの特徴量に対しても、平均(mean)が10^-16とほぼ0で、分散(std)が1になっていることが分かります。あくまで、平均と分散を基にした処理なので、最大値、最小値は各特徴量でバラバラになっていることが分かります。
3.2. 主成分分析(30成分)
データの前処理が出来たので、早速主成分分析を行っていきましょう。まずは、特徴量の数と同じ数だけ主成分を設定し、学習させてみます。
from sklearn.decomposition import PCA
# 主成分分析の学習(30の主成分で抽出, 教師なし学習)
pca = PCA(n_components=30) # n_components:抽出したい主成分の数
pca.fit(X_train_scaled)
学習が完了しました。得られた各主成分の分散の割合(=寄与率)を確認してみましょう。
# explained_variance_ratio_:各主成分が持つ分散の比率
print(pca.explained_variance_ratio_)
> [4.33151261e-01 1.95865064e-01 9.57061086e-02 6.68256792e-02
5.71099742e-02 4.02177092e-02 2.17658540e-02 1.48998125e-02
1.41051623e-02 1.17646492e-02 1.04466423e-02 8.92872287e-03
7.85431930e-03 5.01584805e-03 3.13322648e-03 2.65044932e-03
1.98943309e-03 1.68551393e-03 1.49667384e-03 1.05953262e-03
1.05116615e-03 8.54150580e-04 7.21294486e-04 6.01226101e-04
5.47278774e-04 2.60309706e-04 2.16631872e-04 4.69695401e-05
2.56644788e-05 3.67268770e-06]
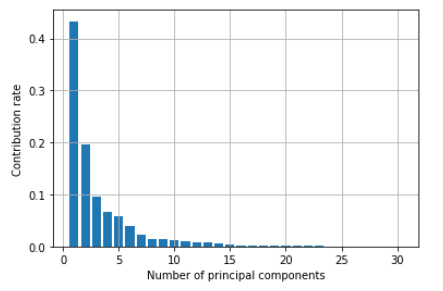
第1主成分で元のデータの43.3%、第2主成分で19.5%の情報を持っていることが分かります。数字だけだと分かりづらいですね。各主成分の寄与率と、累積寄与率をグラフ化してみます。
# 主成分のグラフ化
plt.bar([n for n in range(1, len(pca.explained_variance_ratio_)+1)], pca.explained_variance_ratio_)
plt.ylabel("Contribution rate")
plt.xlabel("Number of principal components")
plt.grid()
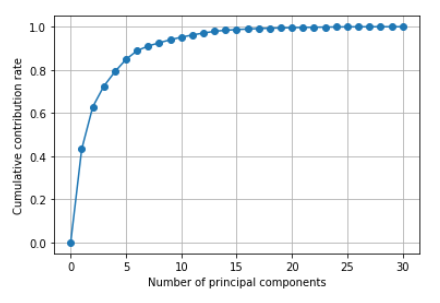
plt.plot([0] + list(np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.ylabel("Cumulative contribution rate")
plt.xlabel("Number of principal components")
plt.grid()
累積寄与率のグラフから、第5主成分までで80%以上の情報を持っていることが分かります。
3.2. 主成分分析(2成分)
2成分まで次元圧縮をして散布図を作成してみましょう。
# PCA 次元数2まで圧縮
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
print(pca.explained_variance_ratio_)
> [0.43315126 0.19586506]
# データを主成分空間に写像
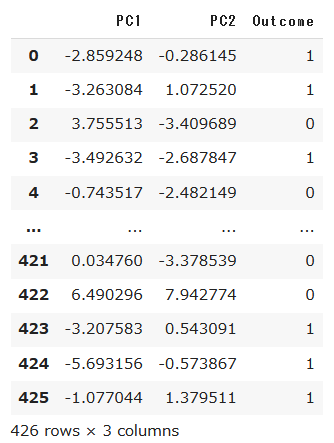
df_pca = pd.DataFrame(X_train_pca, columns=["PC{}".format(x+1) for x in range(2)])
df_pca['Outcome'] = y_train.values # 分類結果も表に併せる
df_pca
# 散布図にプロット
m = df_pca[df_pca['Outcome'] == 0]
b = df_pca[df_pca['Outcome'] == 1]
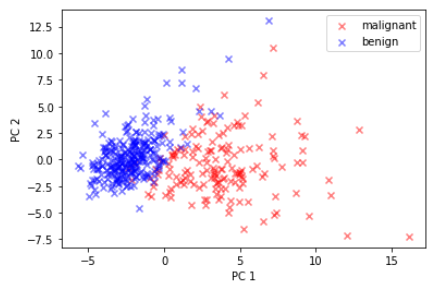
plt.scatter(x=m['PC1'], y=m['PC2'], label='malignant', c='r', marker='x', alpha=0.5)
plt.scatter(x=b['PC1'], y=b['PC2'], label='benign', c='b', marker='x', alpha=0.5)
plt.legend()
plt.xlabel('PC 1')
plt.ylabel('PC 2')
この2つの主成分のグラフを見ると、malignant(悪性, 赤色)とbenign(良性, 青色)が概ね分離出来ていることが分かります。主成分分析はロジスティック回帰などの教師あり学習とは異なり、教師なし学習です。あくまで、データの分散情報を基にデータを回転させているだけになります。このグラフを見ると、悪性と良性のプロットがわずかに重なっていますが、第1主成分と第2主成分で基のデータの62.8%(=43.3%+19.5%)の情報に留まっていることが要因と考えられます。
3.3. 主成分の結果を用いたクラスタリング
ここまでに行ってきた主成分分析はあくまで教師なし学習ですので、前節の最後に示したグラフは、実際にはPC1とPC2のグラフから分類(色分け)までは実行されません。(※今回は教師データ(=分類結果)があったので、色分けして分類を実施しました。)
仮にこの教師データがなかった場合を想定したときに、主成分分析をして得られた結果を活用して教師なし学習であるクラスタリングを実施してみましょう。今回は、scikit-learnのsklearn.cluster.KMeansを利用してみました。(※k-meansの解説は別記事で実施します。)
from sklearn.cluster import KMeans
# クラスター数を2に設定(悪性、良性)
model = KMeans(n_clusters=2)
# pcaデータを基にクラスタリング
y_pred = model.fit_predict(X_train_pca)
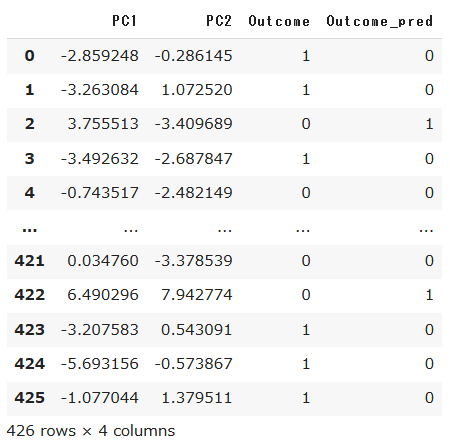
df_pca['Outcome_pred'] = y_pred
df_pca
実際の教師データとk-meansで得られたクラスターで0, 1は逆転してそうですが、概ね予測結果は一致していそうです。(クラスター0がおそらく悪性=1判定)
ちょっとわかりづらいので、0、1を逆転させます。
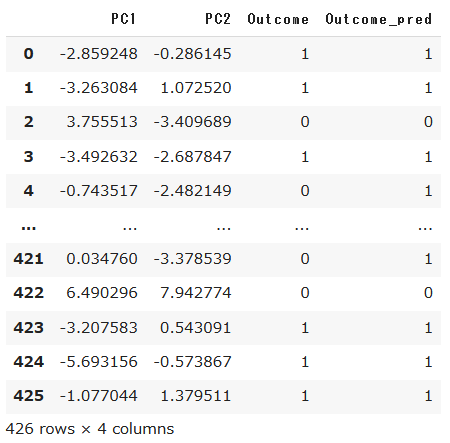
df_pca['Outcome_pred'] = df_pca['Outcome_pred'].map({1 : 0, 0 : 1}).astype(int)
df_pca
それでは、グラフにしてみましょう。
pred_kmeans_1 = df_pca[df_pca['Outcome_pred'] == 0]
pred_kmeans_2 = df_pca[df_pca['Outcome_pred'] == 1]
# 教師データを基にしたデータをリファレンスとしてプロット
plt.scatter(x=m['PC1'], y=m['PC2'], label='malignant', c='r', marker='x')
plt.scatter(x=b['PC1'], y=b['PC2'], label='benign', c='b', marker='x')
# クラスタリングの結果をプロット
plt.scatter(x=Ir1[0], y=Ir1[1], label='Ir1', c='b', alpha=0.5)
plt.scatter(x=Ir2[0], y=Ir2[1], label='Ir2', c='r', alpha=0.5)
plt.legend()
plt.xlabel('PC 1')
plt.ylabel('PC 2')
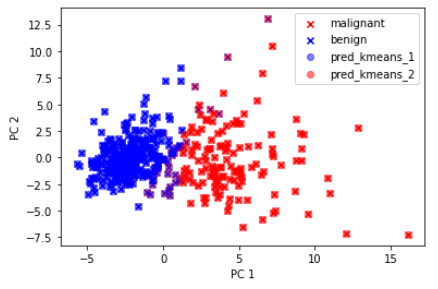
k-meansにより2つのクラスターが得られ、リファレンス(xプロット)に対して、結果が概ね一致していることが分かります。但し、分類の境界線のあたりが、k-meansでのクラスターが良性(青〇プロット)なのに、実際の結果は悪性(赤×プロット)という結果もあり、誤差は大きそうですね。
k-meansは教師なし学習ですが、本データセットは教師データがあるので、クラスタリングの評価をしてみましょう(※本来は教師データがないはずなので、評価はできません)。教師あり学習の分類で活用した混同行列で評価してみます。
from sklearn.metrics import confusion_matrix
confusion_matrix = confusion_matrix(df_pca['Outcome'].values, df_pca['Outcome_pred'].values)
confusion_matrix
> array([[128, 31],
[ 7, 260]])
良性(=1)と予測して、悪性(=0)だった点が31点あります。今回はがんのデータセットですので、このモデルでの診断は危険そうです(良性判断の患者が見落とされ、病状が悪化する可能性があるため)。
今回は教師データがあるので併せてプロットを行いましたが、本来は教師なし学習の場合、教師データがないので結果を評価するには人間が確かめるしかありません。
(番外編)ロジスティック回帰による分類
主成分分析とk-meansを使ってクラスタリングを実施しましたが、今回のデータセットは教師データも付属しているので、ロジスティック回帰モデルで分類をしてみましょう。ロジスティック回帰については、こちらの記事で使い方を説明しています。
# ロジスティック回帰モデルの学習
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import confusion_matrix
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_scaled, y_train)
# 学習モデルの検証
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
print('Confusion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))
> Train score: 0.988
Test score: 0.972
Confusion matrix:
[[50 3]
[ 1 89]]
30個の特徴量を使って学習させたロジスティック回帰モデルは、検証データの決定係数R^2=0.97と、かなり高い精度で悪性、良性を分類出来ています。
4. おわりに
今回は、乳がんデータセットを主成分分析により解析を実施しました。30個の特徴量を、約70%の情報を持つ2変数まで次元削減をすることで、2軸にプロットすることができ、構造をわかりやすく可視化することができました。
機械学習入門のリンク
今後も引き続き機械学習の実装入門を記事にしていきます。
参考にどうぞ。
・線形回帰モデル
・非線形回帰モデル
・k-近傍法
・ロジスティック回帰モデル
・主成分分析 本記事
・K-means
・サポートベクターマシン ※今後更新予定