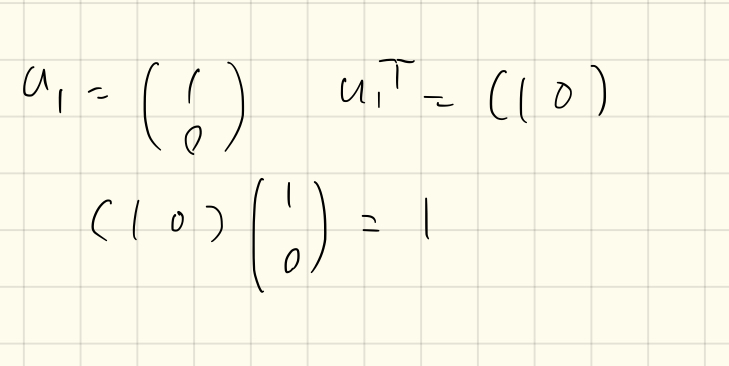主成分分析とは
主成分分析(Principle Component Analysis)とは,どういったものなのかを説明したいと思います.主成分分析は多次元のデータを次元圧縮(データは減らない)する方法です.
主成分分析とは直接は関係ありませんが,次元圧縮の一例として例えばプログラマのスキルとしてpython,Java,給料でプログラマのの熟練度を測るためにGithub上でのstar⭐️の数でスキル(2次元とする)を評価できると仮定しましょう.
それはつまり3次元のデータを2次元に要約(圧縮)したことになります.
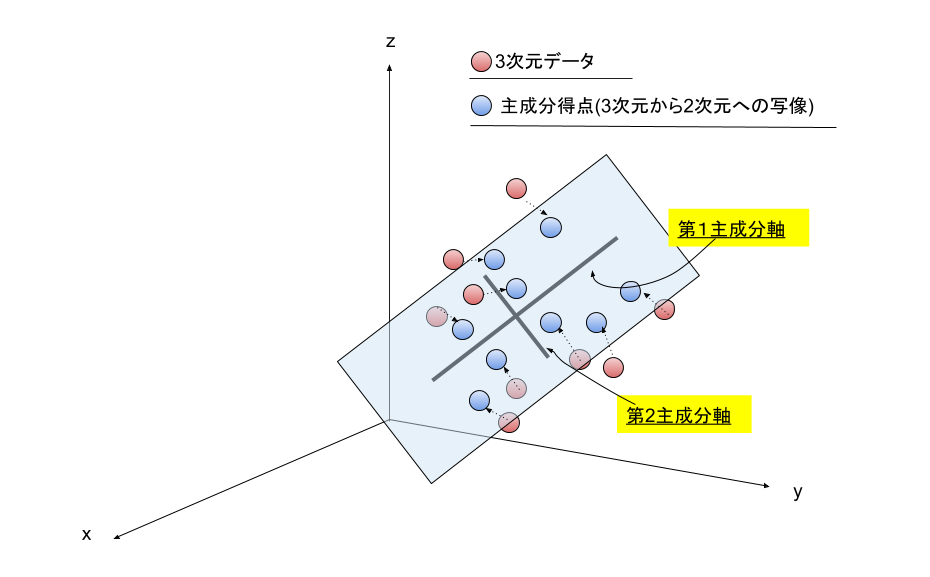
次に3次元から2次元への写像($f:\mathbb{R}^3 \to \mathbb{R}^2$)を考えた主成分分析とは、座標で考えると,例えば3次元のデータ(x,y,z座標)を二次元のデータ(l,m座標)に要約(圧縮)するようなものです.
この時,第n主成分を分散の大きい順に,l(エル)を第1主成分,mを第2主成分と呼びます.
イメージとしては,三次元空間にある赤い点を主成分軸(この場合第1・第2主成分)にして2次元で表すということです.
本記事では,3次元を2次元に圧縮する例を紹介します.
誤解してほしくないこと
今回は3次元から2次元への射影を考えますが,100次元から10次元への圧縮でも主成分分析を使えばそれは主成分分析です.Twitterに誤解して覚えてる人がいましたが”空間を面に、面を直線に落とし込んでいる”わけではありません.
主成分分析は次元圧縮のアルゴリズムというだけで、分かりやすいように3次元から2次元への射影を表現しているに過ぎません.高次元では高次元多様体から低次元多様体への次元圧縮を計算していると考えても良いかもしれません(※多様体学習を参照)が,射影できる次元が特別決められているわけではありません.詳しくはPRMLの下巻を参照してください.
主成分軸をどのように見つけるのか.
主成分を見つけるためには,分散が最大になるような軸を探します.
分散はどのようなものかといえば以下の式のようにデータ$x_i$とデータ平均$\mu$の二乗和を平均nで割ったものです.(端的に言ってしまえば,データの散らばり具合を定義していることになります.)
分散の定義
Var[X] = E[(X - \mu)^2] = \frac{1}{n} \sum_{i=1}^n(x_i - \mu)^2
この時Xを確率変数といいます.右辺の$x_i$と同じです.定義から$x_i =\mu$の時分散は0になり,$\mu=0$のとき分散は最大となります.($\mu > 0$)
分散が最大となる軸を探すというのことは軸に最も近い確率変数を探すということになります.
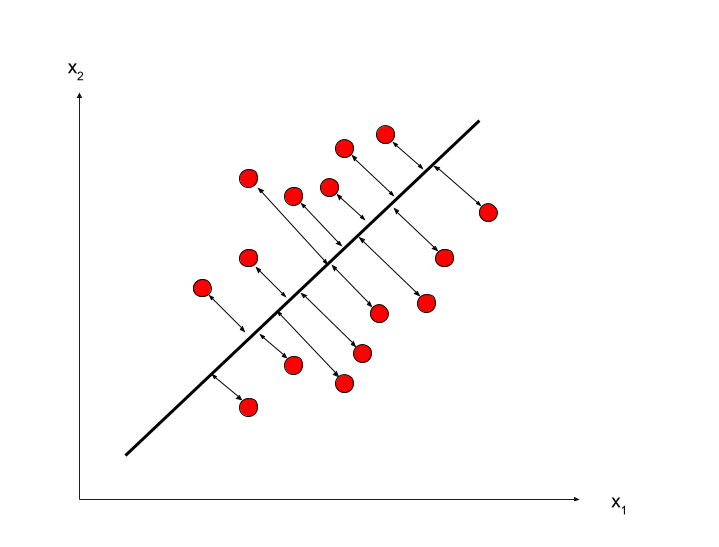
下の図のような具合にデータが散りばめられている時分散は小さくなり情報の損失は大きくなります.
それに対して,ほぼありえないことですが,直線にぴったし確率変数が当てはまった場合は分散は最大になり情報の損失は0になります.(下の図)
このような軸を求めるのが主成分分析の目標です.

固有値と固有ベクトル
固有値と固有ベクトルの定義
n次正方行列において,
$A \vec{v} = \lambda \vec{v}$ を満たす零ベクトルではないn次元実数ベクトル,
$\vec{v} \neq \vec{0}_n$ とスカラー**$\lambda$** が存在するとき,
$\lambda$ をAの固有値. **$\vec{v}$**をAの($\lambda$に対する)固有ベクトルという.
これだけでは何を言っているか分からないので実際に計算をしてみる.
実際には行列に対して固有多項式を定義してやりそれを解くことによって求まる.
固有多項式の定義
$n$次正方行列Aに関して
|A - \lambda E| = 0
をAの固有方程式という.
例
以下の2次正方行列の固有値と固有ベクトルを求めよ.
A =
\begin{pmatrix}
a & b \\
c & d \end{pmatrix}
固有方程式は代入すればいいだけなので,
|A-\lambda E| = |\begin{pmatrix} 1 & 2 \\ 3 & 2 \end{pmatrix} - \begin{pmatrix} \lambda & 0 \\ 0 & \lambda \end{pmatrix}| \\
\\
= |\begin{pmatrix} 1-\lambda & 2 \\ 3 & 2-\lambda \end{pmatrix}|
あとはサラスの公式で計算すればいいだけなので,
$= (1-\lambda)(2-\lambda)- (2 ・ 3)$
$=\lambda ^2 -3\lambda -4$
$=(\lambda + 1)(\lambda -4) = 0$
よって$\lambda = -1,4$
固有値$\lambda_1=-1$に対する固有ベクトル
\vec{p} = \begin{pmatrix}p_1 \\ p_2 \end{pmatrix} を求める.
\begin{pmatrix}1 & 2 \\ 3 & 2\end{pmatrix} \begin{pmatrix}p_1 \\ p_2 \end{pmatrix} = (-1)\begin{pmatrix}p_1 \\ p_2 \end{pmatrix} \\
\Rightarrow p_1 + 2p_2 = -p_1, 3p_1 + 2p_2 = -p_2 \Rightarrow p_1 = -p_2
連立方程式を解くと
$3p_1 = -3p_2 = p_1 = -p_2$となる.
よってスカラー$\kappa \neq 0$を用いて$\lambda_1$に対応する固有ベクトル$\vec{p}$は次式で与えられる.
\vec{p} = \kappa \begin{pmatrix} 1 \\ -1 \end{pmatrix} ただし \kappaは0以外の整数(k \neq 0)
また固有値$\lambda_2 = 4$に対する固有ベクトルは
\vec{q} = \begin{pmatrix} q_1 \\q_2 \end{pmatrix} を求める.
上と同じ手順に解くと$\lambda_2=4$に対する固有ベクトル$\vec{q}$が求まる.
\vec{q} = \kappa \begin{pmatrix} 1 \\ \frac{3}{2} \end{pmatrix} (k \neq 0)
寄与率と累積寄与率
次に寄与率についての説明です.第1主成分と第2主成分の定義は以下になります.
第1主成分の寄与率は第1主成分がデータ全体のデータの散らばり具合をどれくらいカバーしているかを表しています.第2主成分以降も同様です.
第1主成分の寄与率 = $\frac{(第1主成分の固有値)}{(第1主成分の固有値)+(第2主成分の固有値)}$
第2主成分の寄与率 = $\frac{(第2主成分の固有値)}{(第1主成分の固有値)+(第2主成分の固有値)}$
一般に第i主成分までの定義は以下になります.
第i主成分の寄与率 = $\frac{l_i}{総分散}$ = $\frac{l_i}{総固有値}$
総分散 = $\Sigma^n_{i=1}l_i$ (ただし $l_i$は第i固有値)
累積寄与率
累積寄与率とは,第1主成分から第m主成分までの寄与率の和です.
第1主成分から第m主成分での圧縮がデータの散らばり具合をどの程度カバーしているかの説明する割合です.(1に近ければデータの散らばり具合を説明できている割合が高いことになります.)
第1主成分から第m主成分までの累積寄与率 = $\frac{l_1+l_2 + \cdots + lm}{総分散}$
(分散共分散行列で求めた固有値は,主成分方向の分散に対応します.)
$Su_1=\lambda_1u_1$これに左から$u_1^T$を書けると
$u_1^TSu_1=\lambda_1$で与えられ,したがって分散は,$u_1$を最大固有値$\lambda_1$に属する固有ベクトルに選んだときに最大となります.この固有ベクトルとを第1主成分といいます.その他の主成分も主成分ベクトルに直行するという条件の下で,射影分散を最大にするような方向を選ぶことで逐次的に得ることが出来ます.
一般的にはM次元の射影空間を考えれば,データ共分散行列Sの大きい順にM個の固有値$\lambda$に対応する固有ベクトル$u$を選んだあげれば,射影されたデータの分散を最大にする最適な線形射影が定義されます.
以上のことが主成分分析の全てだと思います.分散に対応する最大固有値に対応する固有ベクトルを選ぶことによって,データを圧縮していると考えられます.
相関があるとデータを射影しやすいというのは以上のことから考えることが出来ると思います.
分散共分散行列についてはこちらがわかりやすいです.
https://mathtrain.jp/varcovmatrix
参考PRML 下 p277~p288
実際に応用して見る.
PythonとJavaのソースコードのGithub上でのスターの総数と給料という3次元のデータを2次元に次元圧縮する例を考えてみました.あたいはある程度相関があるように適当に調整しました.(現実とはおそらく異なるでしょう....)
pythonのscikit-learnのPCAのライブラリを使用しました.
| 点の色 | Pythonのstar⭐️の総数 | Javaのstar⭐️の総数 | 給料(万円) |
|---|---|---|---|
| 青 | 70 | 30 | 700 |
| 緑 | 32 | 60 | 480 |
| 赤 | 32 | 20 | 300 |
| 黄色 | 20 | 120 | 600 |
| 茶色 | 40 | 120 | 630 |
| グレー | 40 | 30 | 520 |
| ディープピンク | 300 | 1100 | 1200 |
| 黒 | 2000 | 400 | 1500 |
| オレンジ | 40 | 180 | 800 |
import matplotlib.pyplot as plt
import numpy as np
# 主成分分析をするライブラリ
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# [Pythonのコードのスター総数, Javaのコードのスターの総数, 年収]
X = np.array([[70, 30, 700],[32, 60, 480],[32, 20, 300],[20, 120, 600],[40, 120, 630], [40, 30, 520], [300, 1100, 1200], [2000, 400, 1500],[40, 180, 800]])
pca = PCA(n_components=2)
pca.fit(X)
# 各主成分によってどの程度カバー出来ているかの割合(第一主成分,第二主成分)
print(pca.explained_variance_ratio_)
# 次元削減をXに適用する.
pca_point = pca.transform(X)
fig = plt.figure(figsize=(10,10))
fig.suptitle("$R^3$ to $R^2$ mapping", fontsize=16)
ax1 = fig.add_subplot(221, projection='3d')
ax2 = fig.add_subplot(222)
color = ['blue', 'green', 'red', 'yellow', 'brown', 'gray', 'deeppink', 'black','orange']
ax1.set_title("3 dimension space")
ax1.scatter3D(X[:,0],X[:,1],X[:,2],color=color)
ax2.set_title("2 dimension space")
ax2.scatter(*pca_point.T, color=color)
plt.show()
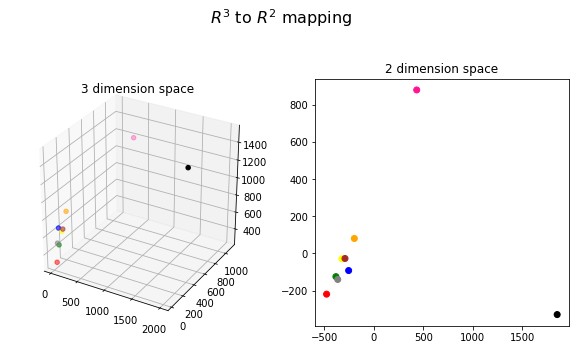
主成分得点をプロットすると以下のグラフになる.
**x軸に相当するのが給料と見ることができるでしょう.y軸に相当する方向の解釈が難しいですが,よーくデータ分布を見るとJavaができて給料がそこそこの人が高くなる傾向にあるように見ることができそうです.**黒の人は給料は高いがpythonで勝負している人と解釈できそうだ.ピンクさんは給料が高くpythonよりもjavaが得意な人と見ることができそうです.
他の人たちもだいたい同じ規則でしたがっていそうです.
正直に言うと完璧な解釈などこの世には存在しません.解釈は自由で良いのです.
まとめ
最後のはデータをQiitaのアドベントカレンダーように急いで作ったのであくまで参考程度に解釈してほしい.自然のリアルなデータだと主成分分析は気づかない特徴を調査することができるので使えるだろう.またカーネルPCAなどもあるが私の現在のレベルでは難しいのでもう少しレベルアップしたらどこかで書きたい.
また,主成分分析では主成分軸を見つけて関係している因子を自分で解釈するが,逆の発想で因子を自分で仮定して推定する手法に因子分析というものがある.それはおいおい書けたら書きたいと思う.
追記
渡辺澄夫先生のページから
http://watanabe-www.math.dis.titech.ac.jp/users/swatanab/dataan201905.pdf

主成分分析の目的を面白く書かれておりました。考えてみると勉強になると思います。
参考文献
統計科学研究所_R_主成分分析.ppt から数式など参照させてもらいました.
固有値の計算手順や主成分分析の考え方などの文言など.
線形代数学に基づくデータ分析法: 原田 史子,島川 博光
WhisponMLCafe.はAI受託開発しております。気軽にご相談ください。