【機械学習】ロジスティック回帰の実装

ロジスティック回帰による分類を実装します。
参考にした文献は以下のものです。

「機械学習を理解するための数学のきほん」　著：立石賢吾

ロジスティック回帰とは

ロジスティック回帰（ロジスティックかいき、英: Logistic regression）は、ベルヌーイ分布に従う変数の統計的回帰モデルの一種である。連結関数としてロジットを使用する一般化線形モデル (GLM) の一種でもある。1958年に David Cox が発表した[1]。確率の回帰であり、統計学の分類に主に使われる。医学や社会科学でもよく使われる。(Wikipedia)

標本データを２値、あるいは多値に分類する教師あり学習の方法の一つ。
他の分類はデータの量的変数を算出するのに対して、ロジスティック回帰はデータの発生確率を算出する。

ロジスティック回帰による分類の目的

標本データを分類し、その上でその分類が成立する確率を各入力値について算出する。

実装に当たって必要な概念

シグモイド関数

シグモイド（英: sigmoid）とは、ギリシア文字シグマ (σ) の語末形（ς）に似た形のこと。S字形ともいう。
特に各種グラフに現れるシグモイド曲線 (英: sigmoid curve) を指す。このようなグラフは個体群増加や、ある閾値以上で起きる反応（例えば急性毒性試験での死亡率）などに見られる。(Wikipedia)

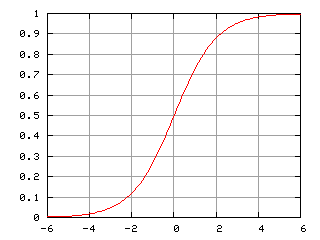
シグモイド関数は以下のような数式及びグラフで表される。

シグモイド関数

f_θ(x) = 1 / (1 + exp(-θ^T * x))

シグモイド関数 fθ(x) の取りうる値域は 0 < fθ(x) < 1 であるため、分類の成立確率を算出するロジスティック回帰との相性が良い。

決定境界

シグモイド関数は入力値に対する分類の成立確率を示す関数であるから、決定境界とはならないため別の計算式が必要となる。

シグモイド関数を fθ(x) と置いた時、次の式が成り立つ。

θ^Tx >= 0 のとき、 y = 1\\
θ^Tx < 0 のとき、 y = 0

シグモイド関数では、分類確率 0.5 が確率の中間地点となっている。
その中間地点における横軸 θTx は０であるため、シグモイド関数により算出された分類確率が 0.5 以上であれば(θTx が０以上であれば)分類Aに、それ以外であれば(θTx が０未満であれば) 分類B へ、という振り分け方で決定境界を決めることができる。

尤度関数

尤度関数（ゆうどかんすう、英: likelihood function）とは統計学において、ある前提条件に従って結果が出現する場合に、逆に観察結果からみて前提条件が「何々であった」と推測する尤もらしさ（もっともらしさ）を表す数値を、「何々」を変数とする関数として捉えたものである。また単に尤度ともいう。(Wikipedia)

標本データに於いて、それぞれの入力値が正解値と紐づけられる分類確率の総和は以下のように表せる。

L(θ)=ΠP(y^{(i)} =1|x^{(i)}){y^{(i)}}P(y^{(i)} = 0 | x^{(i)})^{1-y^{(i)}}

和訳：
全体の発生確率 L は、変数xについて、
①Aと分類される確率[P(y = 1 | x)]
②Bと分類される確率[P(y = 0 | x)]
を全て乗算したものである。

ここでいう分類確率とは入力値が正解値と紐付く可能性であり、L(θ) はその乗算結果であるから、 L(θ) が最大になるようにパラメータ θ を設定することが目的となる。

最小二乗法では誤差の総和 E(θ) を求めていたのでそれが最小となるようにθを設定したが、ロジスティック回帰では最大を求めることに注意する。

尤度関数の対数をとり計算を簡略化すると以下のような形になるので、それをパラメータ更新式で用いる。

Σ(y^{(i)} - fθ(x^{(i)}))x_j^{(i)}

パラメータ更新式

パラメータ θ の更新式は次のようになる。

θ_j := θ_j + ηΣ(y^{(i)} - fθ(x^{(i)}))x_j^{(i)}

ロジスティック回帰の実装

##目標
入力値と正解値が正しく紐付く確率が最大になるようなパラメータ θ を発見し、その値を用いて決定境界及びロジスティック回帰モデルを生成する。

実装の流れ

①データの準備
②シグモイド関数の実装
③パラメータ更新式の実装
④パラメータの更新
⑤結果の確認

実装

ロジスティック回帰の実装

import numpy as np
from matplotlib import pyplot as plt

#①------------------------

#別途用意したcsvからデータを読み込む
test = np.loadtxt('0226.csv',delimiter=',',skiprows=1)

#標本データの抽出。元データの２列を読み込み、以後ベクトルとして扱う
train_x = test[:,0:2]
#正解値の抽出
train_y = test[:,2]

#パラメータの初期化。ベクトル同士の乗算を成立させるため、１行３列のデータを設定。
theta = np.random.rand(3)


#標準化関数の実装
#平均
mu = train_x.mean()
#分散
sigma = train_x.std()
def standardize(x):
    return (x - mu) / sigma

#標本データの標準化。標準化を行うことで、データの平均を０に、分散を１に慣らすことができる
train_x = standardize(train_x)


#ベクトル同時の乗算を成立させるため、標本データに０列目を追加する
def add_x0(x):
    #標本データの行数分、要素１の行データを生成する
    x0 = np.ones([x.shape[0],1])
    #生成した行データを、標本データの直前に置いて結合する
    return np.hstack([x0,x])


#標準化され、かつ０列目に要素１のデータが設定された標本データ
X = add_x0(train_x)


#②③---------------------


#識別関数としてのシグモイド関数を実装
def f(x):
    #θ群と変数群をそれぞれベクトルと見なし乗算を行なっている
    return 1 / (1 + np.exp(-np.dot(x, theta)))


#学習率の定義。厳密な規定はない。
ETA = 1e-3

#指定回数パラメータの更新を行う更新式を実装
def update_theta():
    new_theta = theta + ETA * np.dot(train_y - f(X), X)
    return new_theta


#④----------------------


#更新回数の指定
epoch = 5000


print('更新前のパラメータθ')
print(theta)

#パラメータ更新の実行
for _ in range(epoch):
    theta = update_theta()

print('更新後のパラメータθ')
print(theta)


#⑤----------------------


#標本データの可視化
##正解値が１のデータを'o'で可視化
plt.plot(train_x[train_y==1, 0],train_x[train_y==1,1],'o')
##正解値が０のデータを'o'で可視化
plt.plot(train_x[train_y==0, 0],train_x[train_y==0,1],'x')


#描画するグラフのx軸の長さ
xline = np.linspace(-2,2,100)

#決定境界を可視化する関数を実装
def validator(theta):
    #(x,y)におけるy軸。
    #シグモイド関数では θTxa=0 が分類AとBの境界だったので、その時の値を求めてプロットする。
    #θTx = θ0x0 + θ1x1 + θ2x2 = 0
    #x2  = -(θ0 + θ1x1) / θ2
    y = -(theta[0] + theta[1] * xline) / theta[2]
    
    return y

#決定境界の可視化
#plt.plot(x0, -(theta[0] + theta[1] * xline) / theta[2], linestyle='solid')
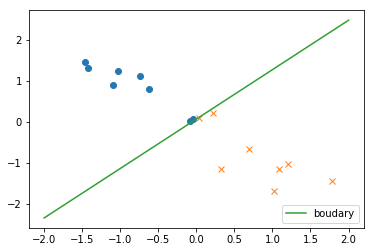
plt.plot(xline, validator(theta), linestyle='solid', label='boudary')
plt.legend(loc='lower right')
plt.show()

print('算出された決定境界の式')
print('y = {:0.3f} + {:0.3f} * x1 + {:0.3f} * x2'.format(theta[0], theta[1], theta[2]))

# 分類確率の可視化
plt.plot(np.reshape(np.arange(X.shape[0]),16,1), np.sort(f(X))[::-1])
plt.ylabel('probability')
plt.xlabel('number')
plt.show()

決定境界

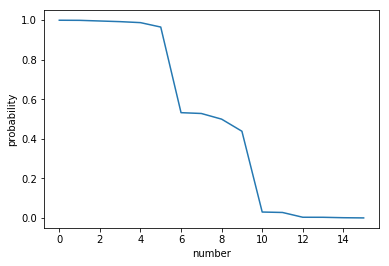
分類確率
初めの及び末尾の６つはほぼ９割以上の確率で分類されることがわかる。
対して真ん中の４データについては、分類確率が５割程度であり精度が怪しいことが見て取れる。

線形分離不可能な問題について

パーセプトロンによる分類では線形分離不可能な問題に対して無力であったが、ロジスティック回帰ではその問題を解決することができる。

使用するcsvデータを変更し、以下のようにコードを書き直すと曲線による分類を再現できる。

線形分離不可能な問題の分類

#パラメータの初期化。二次関数を定義するため、１行４列のデータを設定。
theta = np.random.rand(4)

#ベクトル同時の乗算を成立させるため、標本データに０列目と４列目を追加する
def add_x0_x3(x):
    #標本データの行数分、要素１の行データを生成する
    x0 = np.ones([x.shape[0],1])
    x3 = x[:, 0, np.newaxis] ** 2
    #生成した行データを、標本データの直前に置いて結合する
    return np.hstack([x0,x,x3])

#決定境界を可視化する関数を実装
def validator(theta):
    y = -(theta[0] + theta[1] * xline + theta[3] * xline ** 2) / theta[2]    
    return y

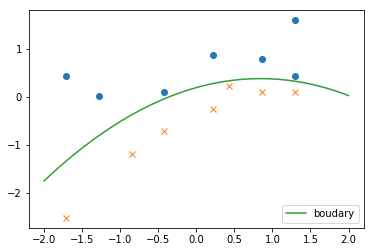
このように決定境界式の次元を上げることで曲線を実現することができるため、パーセプトロンでは解決できなかった線形分離不可能な問題についても対応できる。

以上。