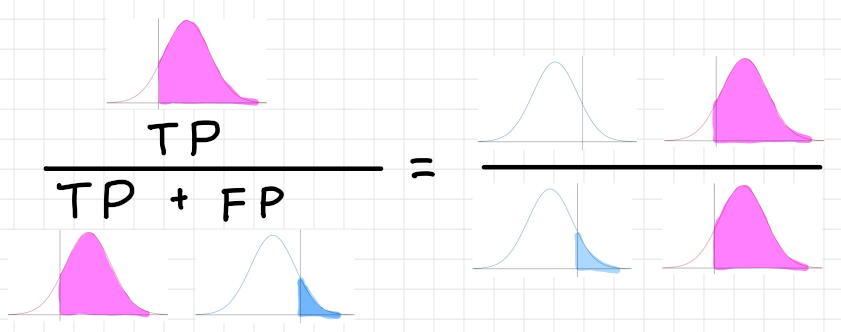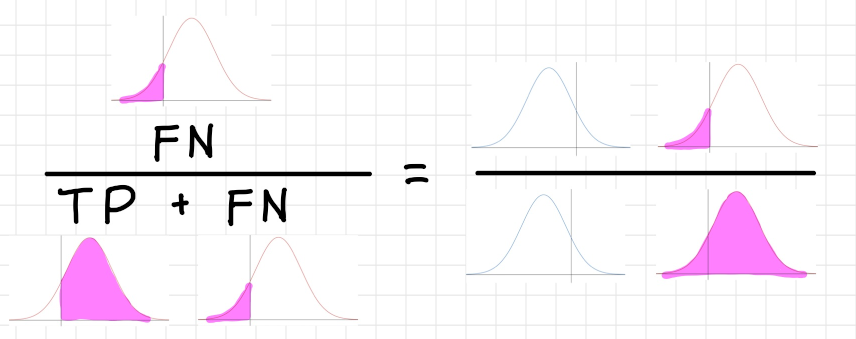混同行列とは(Confusion Matrix) とは
ここでいう混同行列(Confusion Matrix) とは2 値分類問題で出力されたクラス分類の結果をまとめたマトリックス(行列≒表)のことで、2 値分類機械学習モデルの性能を測る指標として使われます。
猫を推測する2 値分類の機械学習モデルを例に混同行列を理解する
ここで2 値分類の機械学習モデルを理解するために、猫である虎さんがオーナーとなっている虎猫鮮魚店でのできごとを例にみていきましょう。
虎猫鮮魚店は新鮮で旬な魚を取り扱っていることで有名で、主婦やおつかいに来た子供、散歩にきたお爺ちゃんお婆ちゃんらからも大人気な街一番の魚屋です。
ところが最近、その新鮮な魚のにおいを嗅ぎつけ猫が寄っては魚を盗んでいくようになりました。
大将の虎さんは「このままではお店の利益が下がり、良くしてくれているお客様に新鮮な魚をとどけられなくなってしまう…」と危機感を抱いていました。
そこで大将の虎さんは最近流行りの機械学習なるものを勉強し、プログラミングも勉強し、監視カメラで猫が映った時にそれを検知するシステムを作ってみました。
では大将の虎さんと一緒に**混同行列(Confusion Matrix)**について学んでいきましょう。
2 値分類の機械学習が行うクラス分類について
2 値分類の機械学習を導入したとしても、2 値分類の機械学習は常に正しい分類をしてくれるとは限りません。 その2 値分類の機械学習が猫を撮影して正しく猫と判断することもありますし、その一方で誤って猫ではないと判断してしまうケースもあります。
そういった2 値分類の機械学習が出した結果と実際の結果との間には以下のようなケースパターンが存在し、次のように呼ばれます。
これらを表にあらわすと以下のようになり、これを**混同行列(Confusion Matrix)**と呼びます。
混同行列を使って、機械学習モデルの性能を測るための指標を以下のように算出することができます。
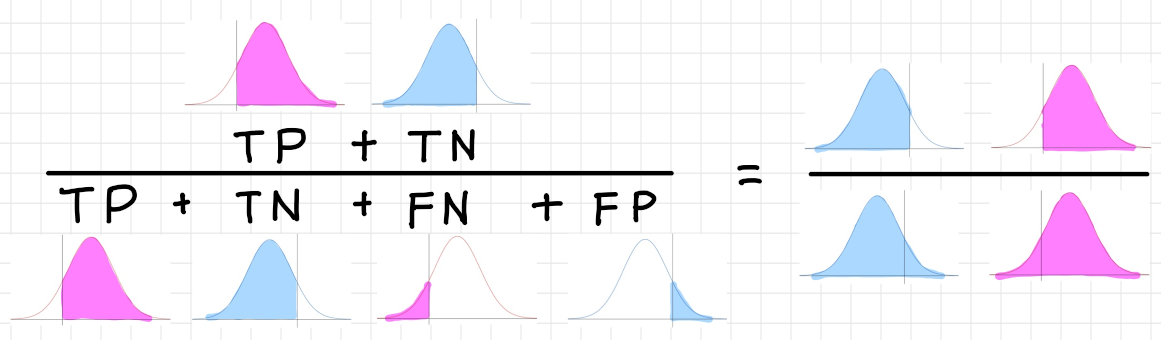
正解率・正確さ(Accuracy)
全体のデータの中で正しく分類できたTP とTN
がどれだけあるかという指標。高いほど性能が良い。
$Accuracy = \dfrac{TP + TN}{TP + FP + FN + TN}$
精度・適合率(Precision)
Positive と分類されたデータ(TP + FP)の中で実際にPositive
だったデータ(TP)数の割合。この値が高いほど性能が良く、間違った分類が少ないということを意味する。
$Presision=\dfrac{TP}{TP + FP}$
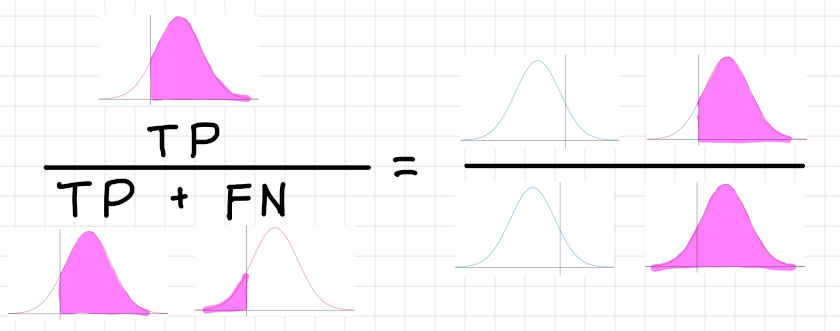
再現率・真陽性率(Recall, True Positive Rate)
取りこぼし無くPositive なデータを正しくPositive
と推測できているかどうか。この値が高いほど性能がよく、間違ったPositive
の判断が少ないということ。別の言い方をすれば本来Positive
と推測すべき全データの内、どれほど回収できたかという指標。
$Recall=\dfrac{TP}{TP + FN}$
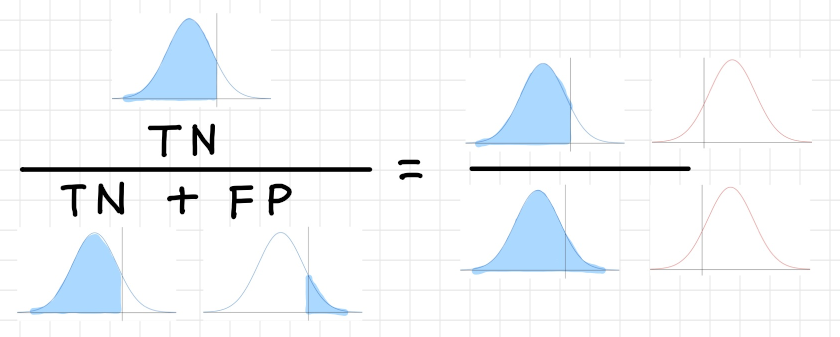
真陰性率(True Negative Rate)
取りこぼし無くNegative なデータを正しくNegative
と推測できているかどうか。この値が高いほど性能がよく、間違ったNegative
の判断が少ないということ。別の言い方をすれば本来Negative
と推測すべき全データの内、どれほど回収できたかという指標。
$True\ Negative\ Rate=\dfrac{TN}{FP + TN}$
偽陰性率(False Negative Rate)
実際にはPositive であるサンプルの内、Negative
であると判定されたクラスの割合。この値が低いほど性能が良い。
$False\ Negative\ Rate=\dfrac{FN}{TP + FN}$
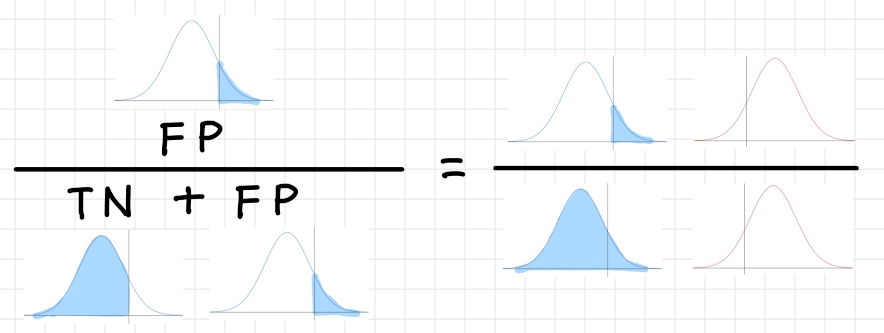
偽陽性率(False Positive Rate)
実際にはNegative であるサンプルの内、Positive
であると判定されたクラスの割合。この値が低いほど性能が良い。
$False\ Positive\ Rate=\dfrac{FP}{FP + TN}$
正解率・正確さ(Accuracy) 以外の指標が必要な理由
正解率・正確さ(Accuracy)だけ指標があれば十分なのでは?思われるかもしれませんが、他の指標が必要である理由があります。例えば虎猫鮮魚店で導入した機械学習モデルを使い、とある1 日の正解率(Accuracy)を集計したところ97% でした。
…これはかなり良い成績では無いでしょうか?
そこで大将の虎さんは閉店後に実際にその日の映像を見て、お店の監視カメラの前を何が通っているのか、そして機械学習モデルのがどのように判断しているかを確認したところ以下のようになりました。
| 物体 | 数 | 猫と推測した数 | 猫でないと推測した数 |
|---|---|---|---|
| 人間 | 900 | 0 | 900 |
| 犬 | 50 | 0 | 50 |
| ヤギ | 15 | 0 | 15 |
| バッファロー | 5 | 0 | 5 |
| 猫 | 30 | 0 | 30 |
この機械学習モデルはすべての人間と犬(+その他猫ではないもの)に対して**猫ではない(Negative)と推測をしていた一方で、すべての猫に対しても猫ではない(Negative)**と推測をしていたのです。
上記の結果より正解率を計算してみると…
$Accuracy = \dfrac{TP + TN}{TP + FP + FN + TN} = \dfrac{0 + 970}{0 + 0 + 30 + 970} = 0.97$
となり正しいですが猫を1 匹たりとも正しく推測することができておらず、使い物になりません…。
このように一見すると正解率が高くて性能の良い機械学習モデルに見えても、実際その蓋をあけてみると、ただひたすら**猫ではない(Negative)**と出力するだけの何も判断しない機械学習モデルとなってしまっているのです。
こういった理由から、正解率(Accuracy)だけでは2 値分類の機械学習モデルの性能を測ることはできないのです。
どれ程猫を正しく猫と判定できるかという性能を測る(再現率・回収率・真陽性率(Recall, True Positive Rate))
そこで役に立つ指標が再現率・回収率・真陽性率(Recall, True Positive Rate)といった指標です。
この指標を使うと本物の猫に対して**猫である(Positive)**と漏れなく推測できているかを計測することができます。
今回の場合、再現率を計算してみると…
$\dfrac{TP}{TP + FN} = \dfrac{0}{0 + 30} = 0$
となり、猫を正しく推測することが全くできていないことがわかります。
そこで虎さんは機械学習モデルを改良して導入し、新たに以下の通り結果が得られたとしましょう。
| 物体 | 数 | 猫と推測した数 | 猫でないと推測した数 |
|---|---|---|---|
| 人間 | 900 | 2 | 898 |
| 犬 | 50 | 20 | 30 |
| ヤギ | 15 | 4 | 11 |
| バッファロー | 5 | 1 | 4 |
| 猫 | 30 | 27 | 3 |
再現率を計算すると以下のようになります。
$\dfrac{TP}{TP + FN} = \dfrac{27}{27 + 3} = 0.9$
正解率・正確さ(Accuracy) は0.95 で変わっていませんが再現性は0.9 と向上し、猫を推測する機械学習モデルとしてはこちらのほうが性能が良くなります。
保守的に猫の判定をしたい(精度・適合率(Precision))
猫を検知したら猫を追い払いたいものの、虎猫鮮魚店は大繁盛店。猫の対応に追われて時間を奪われ、お客さんの対応がおろそかになるのは避けたいところです。
そこで虎さんは猫でないものを誤って猫であると推測してしまう事態はなるべく減らしたいと考えるようになりました。そこで役に立つの指標が精度・適合率(Precision)です。
また、それに加えてROC 曲線の考え方(別記事で説明)を導入して精度・適合率(Precision) の値が大きくなるように閾値を調節して猫の誤検知率を下げることができるのです。
ただし、ここで注意しなければいけないのは、**再現率・真陽性率(Recall, True Positive Rate)と精度・適合率(Precision)は対の関係にあり、一般的に精度・適合率(Precision)を上げると再現率・真陽性率(Recall, True Positive Rate)は下がる傾向にあります。
その点を考慮して、あなたのビジネスモデルを基準に再現率・真陽性率(Recall, True Positive Rate)と精度・適合率(Precision)**を適宜見ながら閾値を調整するようにしましょう。
今回のケースでは虎さんは精度・適合率(Precision)を上げることで再現率・真陽性率(Recall,
True Positive Rate)を下げる結果になり、本物の猫を猫ではないと判断して取りこぼしする可能性も上がることになります。
が、虎さんは猫の対応に追われることにより、お客さんへの対応時間を失うことを心配しているため、この判断はビジネス戦略によって変わってくるものになります。
// 補足: 観点として偽陽性率(False Positive Rate)の値が小さくなるように調整することでも同様な効果を得られます
2 値分類 をビジネスで利用するには
2 値分類の機械学習モデルをビジネスで利用するには性能を測る指標を算出し、目的にあった指標値をしっかりと理解して見ることが重要です。
単に正解率・正確さ(Accuracy) だけを見て2 値分類の機械学習の性能を測るのではなく、再現率・真陽性率(Recall, True
Positive Rate)の指標も組み合わせて利用するようにしましょう。
またROC曲線の考え方も導入して、本当に猫である可能性が高い対象に対してのみ猫であると検知してほしいのか、それとも多少なりとも間違いはあっても取りこぼし無く猫であると検知して拾ってほしいのかといった、ビジネス戦略に沿った閾値を決定することも重要です。
そのあたりを理解したうえで、上手に2 値分類の機械学習モデルを利用するようにしましょう。
ROC 曲線とAUC について
混同行列について勉強したら次はROC 曲線とAUC について紹介していきます。これは別記事まとめましたのでもしよろしければご覧ください。
ROC 曲線とAUC を用いて2値分類機械学習モデルの性能を計測・チューニングする
参考
混同行列(Confusion Matrix)
http://popo.ara.black/etc/confusionmatrix.htm
Confusion matrix (Wikipedia)
https://en.wikipedia.org/wiki/Confusion_matrix
Simple guide to confusion matrix terminology
https://www.dataschool.io/simple-guide-to-confusion-matrix-terminology/