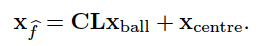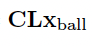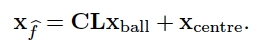はじめに
私がロボットに関して興味を持っており，ロボットの経路を作成したいと思い，経路生成の手法を学んだため，本記事にまとめる．
経路生成の手法は論文として，記載されているがソースコードを探すのに手間がかかったため，自作しようと考えた．
また，私が学生時代にロボットの経路生成に関して研究をしており，理論は理解できてもソースコードを作ることが出来なかった経験をしたため，記事を投稿しようと思った．
本記事に記載すること
・経路生成手法( RRT/RRT-Connect/RRT* )のアルゴリズムをまとめる
・私が作成した経路生成に関する記事の概要およびリンクと将来作成したい記事をまとめる
本記事では記載できないこと (将来作成したい記事)
・RRT/RRT-Connect/RRT* 以外の経路生成手法の記事を作成する
経路生成手法(RRT)のアルゴリズム
経路生成手法(RRT)のアルゴリズムの概要および参考文献を下表にまとめる．
具体的な内容は別章に記載する．
| アルゴリズム | 概要 | 参考文献 |
|---|---|---|
| RRT | 始点から終点までの経路を探索 | J.Kuffner "RRT-Connect: An Efficient Approach to Single-Query Path Planning.", ICRA 2000. |
| RRT-Connect | 始点と終点の両方から経路を探索 | J.Kuffner "RRT-Connect: An Efficient Approach to Single-Query Path Planning.", ICRA 2000. |
| RRT* | RRTに最適性を付与 | S.Karaman, E.Frazzoli "Incremental Sampling-based Algorithms for Optimal Motion Planning.", arXiv 2010. |
| Informed RRT* | RRT*の探索範囲を効率化 | J.D.Gammell, S.S.Srinivasa, and T.D.Barfoot “Informed RRT*: Optimal Sampling-based Path Planning via Direct Sampling of an Admissible Ellipsoidal Heuristic.”, arXiv 2014. |
| Pruning | RRTで作成した経路の経由点を始点側から順番に削除 | R.Geraerts "Creating High-quality Paths for Motion Planning.", The International Journal of Robotics Research 2007. |
| Shortcut | RRTで作成した経路の経由点をランダムで2点選択し，2点間の全経由点を削除 | R.Geraerts "Creating High-quality Paths for Motion Planning.", The International Journal of Robotics Research 2007. |
| Partial Shortcut | RRTで作成した経路の経由点をランダムで2点選択し，2点間の全経由点の情報を修正 | R.Geraerts "Creating High-quality Paths for Motion Planning.", The International Journal of Robotics Research 2007. |
| RRT*-Smart | RRT*の探索範囲を効率化 + 経路最適化 | J.Nasir, F.Islam et al. "RRT*-SMART: A Rapid Convergence Implementation of RRT*", International Journal of Advanced Robotic Systems 2013. |
| RRT*-Connect | RRT-Connectの双方向探索 + RRT*の最適化 | S.Klemm, J.Oberlander et al. "RRT*-Connect: Faster, Asymptotically Optimal Motion Planning", IEEE 2015. |
RRTアルゴリズム
RRTのアルゴリズムを説明する．
参考文献に記載されているRRTのアルゴリズムを抜粋して，下記に記す．
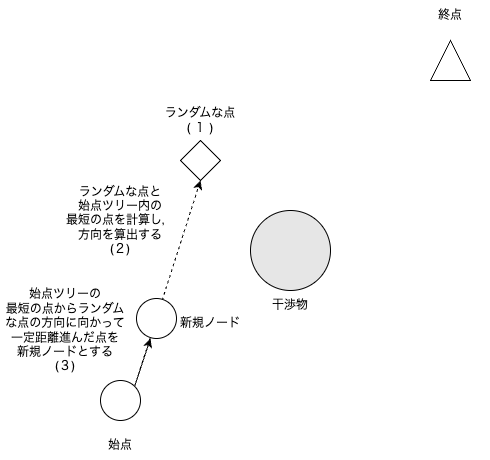
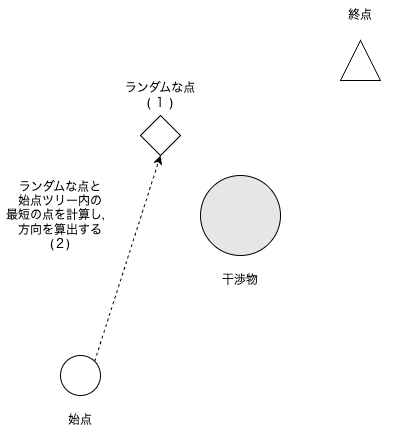
RRTは始点から，終点に向かってどんどんノードを増やしていき，終点との距離がある値以下になったら，経路生成を完了する．
RRTは下図のようなアルゴリズムである．
RRT-Connectアルゴリズム
RRT-Connectのアルゴリズムを説明する．
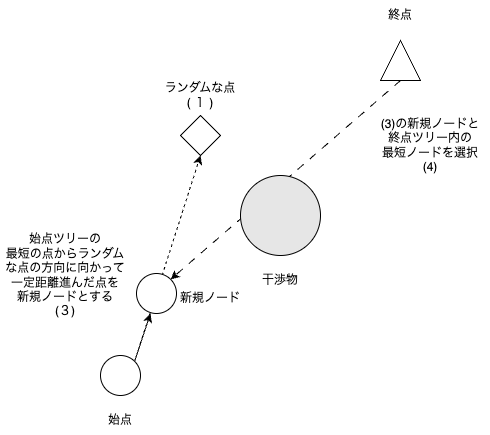
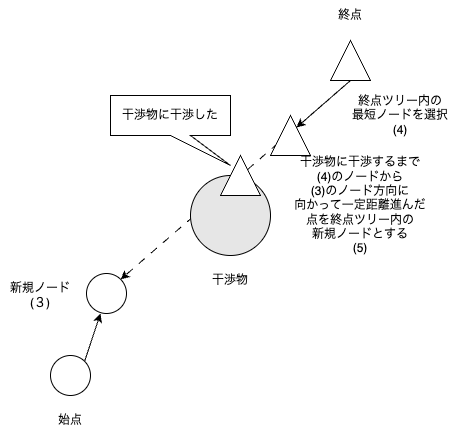
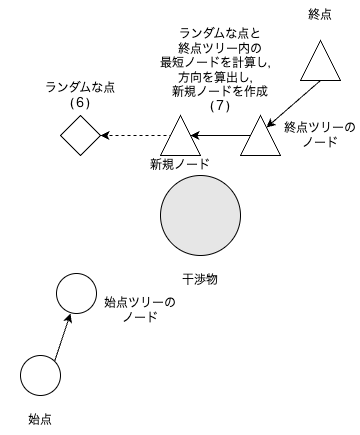
RRT-Connectは始点と終点の両方からノードを増やしていき，始点から終点までノードが繋がれば，経路生成を完了する．
RRT-Connectは下図のようなアルゴリズムである．
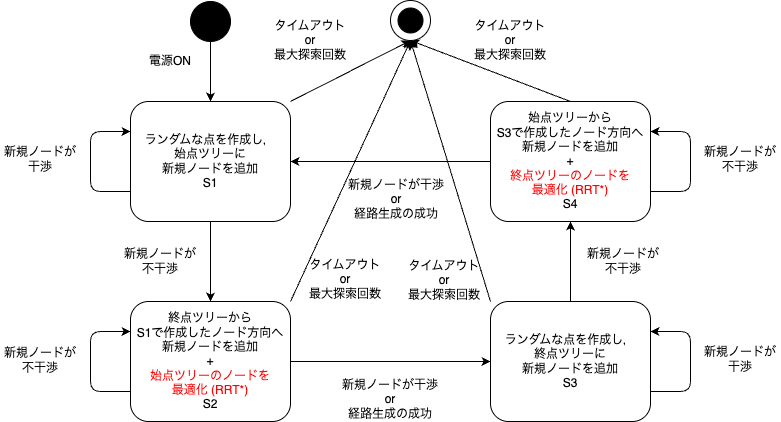
上図のRRT-Connectアルゴリズムより，状態遷移図を作成した．状態としては，下図の通りになる．
RRT*アルゴリズム
RRT*のアルゴリズムを説明する．
参考文献に記載されているRRT* のアルゴリズムを抜粋して，下記に記す．
RRTとの差異を赤枠で記載した．
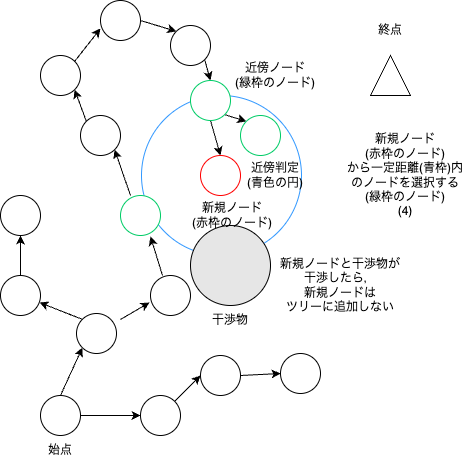
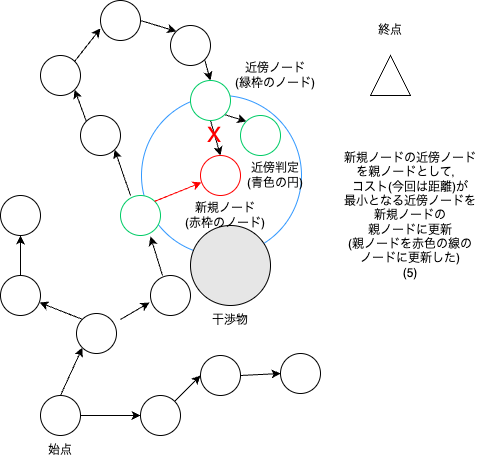
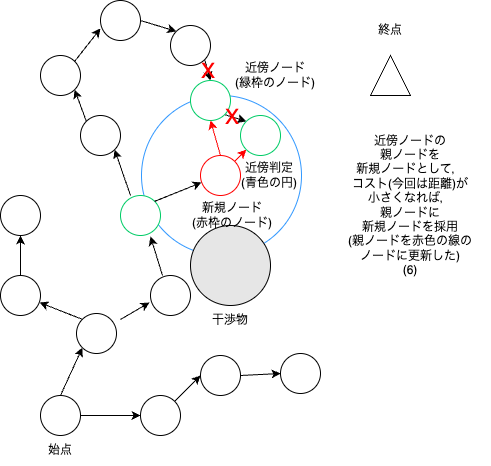
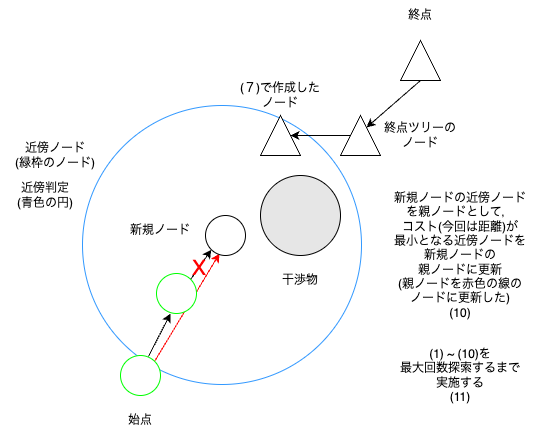
RRT* は始点から，終点に向かってどんどんノードを増やしていき，新規ノードの周辺ノードでコストが最小となるように，親ノードを修正していく．
一定回数実行後に，始点から終点までのコストが最小となる経路を選択する
RRT* は下図のようなアルゴリズムである．
新規ノードを作成した時の近傍ノードを探索する範囲は以下のように定義されている．
\displaylines{
r = R * (\log N / N)^{1/d} \\
r ... 近傍ノードの探索範囲 \\
N ... ツリー内のノード数 \\
d ... 探索空間の次元数 \\
R ... ハイパーパラメータ \\
}
ノード数(N)が多い(探索の試行回数が多い)ほど，近傍ノードの探索範囲(r)は小さくなる．
ハイパーパラメータであるRの値を決めるのが困難である．
Rの値が大きい時のメリット・デメリットは以下の通りである．
メリット
・近傍ノードの数が増えるため，コストが最小となる経路を算出しやすい
デメリット
・処理時間が増える
Informed RRT* アルゴリズム
Informed RRT* のアルゴリズムを説明する．
参考文献に記載されている Informed RRT* のアルゴリズムを抜粋して，下記に記す．
RRT* との差異を赤枠で記載した．
各赤枠内の内容を説明する．
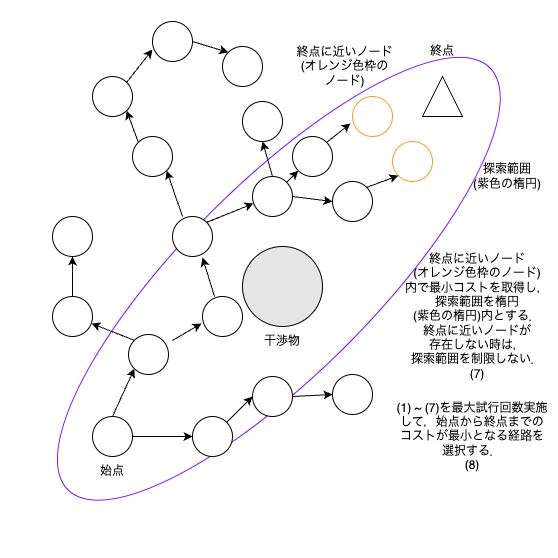
赤枠①：終点に近いノードを保存するためのデータを新規追加
赤枠②：終点に近いノードの中から最小のコストを取得 (終点に近いノードが存在しなければ，コストを無限大と考える)．取得したコストを使用して，ランダムな位置を算出する (詳細は赤枠④に記載)．
赤枠③：新規ノードが終点に近ければ，赤枠①にノードを追加
赤枠④：コストが無限大よりも小さい (終点に近いノードが存在する) 時は，探索範囲を楕円内に制限して，ランダムな位置を算出する．コストが無限大 (終点に近いノードが存在しない) の時は，RRT* と同様に探索範囲は制限せずに，ランダムな位置を算出する．
Informed RRT* は終点に近いノードが存在するまでは，RRT* と同様の処理を実施する．終点に近いノードが存在したら，探索範囲を制限することによってRRT* よりも効率なアルゴリズムとなる．
一定回数実行後に，始点から終点までのコストが最小となる経路を選択する．
Informed RRT* は下図のようなアルゴリズムである．
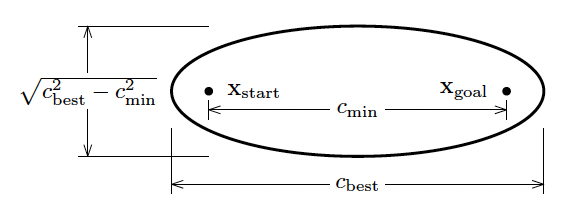
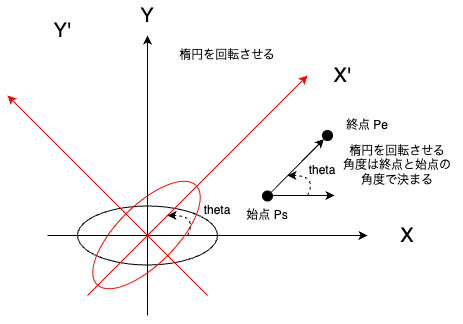
探索範囲を制限する楕円半径は下図のように定義されている．
c_minは，始点と終点のコスト(距離)である．c_bestは，始点から終点までの経路の中での最小コスト(距離)である．楕円の長軸の長さは c_min，楕円の単軸の長さは root(c_best ** 2 - c_min ** 2)だそうだ．
また，楕円内をサンプリングする方法は以下の数式で定義されている．
\displaylines{
x_{center} ... 始点と終点の中点 (ベクトル) \\
x_{ball} ... 単位球内のサンプリング点 (ベクトル) \\
L ... 楕円の各軸の長さを対角要素に持つ対角行列 \\
C ... 始点から終点までの方向ベクトルを座標系とする回転行列 \\
}
数式を分解して，図を用いながら上記数式の内容を説明する．
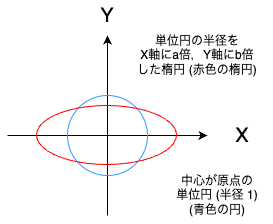
初めに，数式の Lx_ball を説明する．
単位球を楕円に変換している．
次に，数式の CLx_ball を説明する．
楕円を回転させている．回転角度は終点と始点の角度で決まる．
最後に，x_f を説明する．
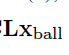
回転させた楕円の中心点を始点と終点の中点に並行移動させている．
上記のようにして，探索範囲を制限する楕円を作成している．
Pruningアルゴリズム
Pruningのアルゴリズムを説明する．
参考文献に記載されているPruningのアルゴリズムを抜粋して，下記に記す．
上記アルゴリズムを説明する．
$N$は，経路を指す．
$2$行目の$|N| - 2$は，経由点数 $- 2$を実施している．経路の中に始点・終点が含まれているため，$-2$を実施することで，始点と終点は選択しないようにしている．
$3$行目の$LP[v_{i}, v_{i+2}] \in C_{free}$は，経路内の$i$要素と$i+2$要素を直線で結び，干渉がなければ$4$行目を実施して，干渉があれば$6$行目を実施する．
$4$行目の$N \leftarrow N / v_{i+1}$は経路$N$から経由点$v_{i+1}$を削除する．
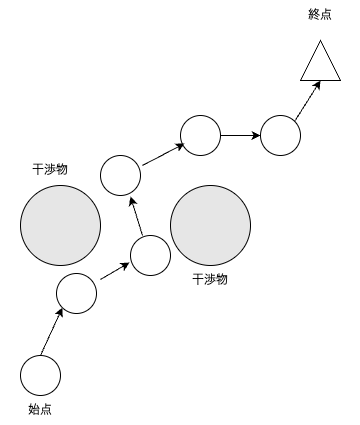
始点側の経由点を順番に削除できるか確認するのが，Pruningである．
PruningはRRTで作成した経路の始点側の経由点から順番に選択していき，選択した経由点前後で干渉判定を行い，干渉がなければ選択した経由点を削除するアルゴリズムである．
Pruningは下図のようなアルゴリズムである．
下図はRRTで作成した経路である．
$i+1$番目の経由点を選択して，選択した経由点前後で干渉判定する．
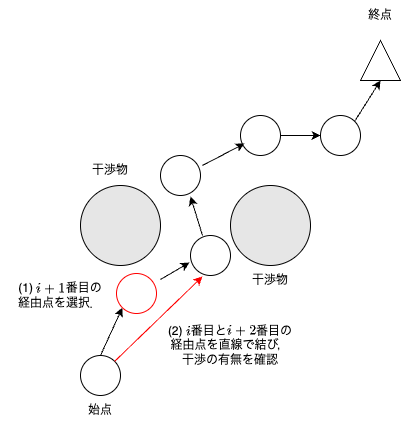
$i+1$番目前後の経由点で干渉なしなら，$i+1$番目の経由点を削除する．
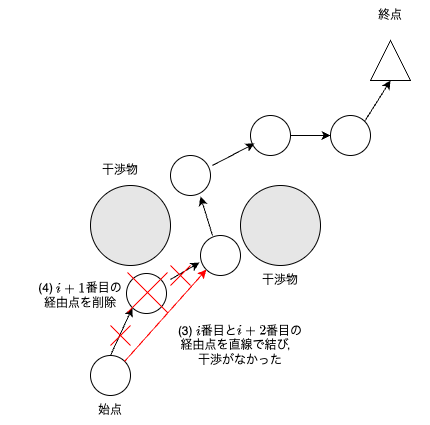
$i+1$番目前後の経由点で干渉ありなら，何もしない(経路は変わらない)．
Pruningによる最終的な経路は下図のようになる．
Pruningを実施することで，環境に依存するが経由点数を減らすことができる．
Pruningはランダムで経由点を選択する訳ではないため，Pruning前の経路が同じであれば，Pruning後の経路は一意に決まる．
Shortcutアルゴリズム
Shortcutのアルゴリズムを説明する．
参考文献に記載されているShortcutのアルゴリズムを抜粋して，下記に記す．
上記アルゴリズムを説明する．
$\prod$は，経路を指す．
$2$行目の$n \leftarrow |\prod|$は，経由点数である．
$3$行目の$a, b \leftarrow$ two random indices $0 \leq a + 1 < b < n$は，$a$と$b$をランダムで選択するが，制約条件も存在する．$a$と$b$が同じ経由点または隣接した経由点を選択しないように制約条件が存在する．
$7$行目の$LP(\pi_{a}, \pi_{b}) \in C_{free}$は，経路内の$\pi_{a}$要素と$\pi_{b}$要素を直線で結び，干渉がなければ$8$行目を実施する．干渉があれば，$loop$の先頭に戻る．
$8$行目の$\prod \leftarrow \prod' \cup LP(\pi_{a}, \pi_{b}) \cup \prod'''$は経路内の$\pi_{a+1}$から$\pi_{b-1}$の経由点を全部削除する．
Shortcutの最大回数分ループする．
ShortcutはRRTで作成した経路から2点をランダムに選択していき，選択した経由点間で干渉判定を行い，干渉がなければ選択した経由点間の全経由点を削除するアルゴリズムである．
Shortcutは下図のようなアルゴリズムである．
下図はRRTで作成した経路である．
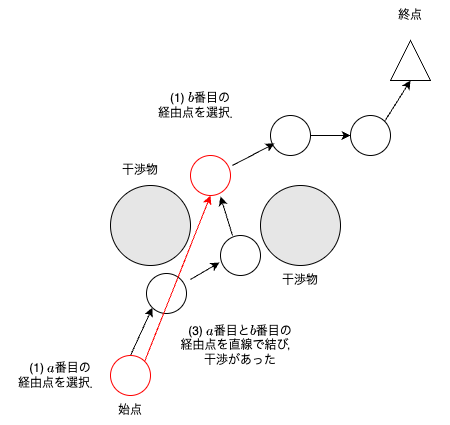
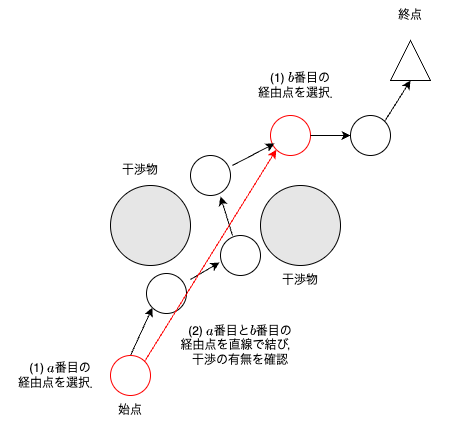
$a$，$b$番目の経由点を選択して，選択した経由点間で干渉判定する．
$a$，$b$番目の経由点間で干渉ありなら，何もしない(経路は変わらない)．
$a$，$b$番目の経由点間で干渉なしなら，$a+1$番目から$b-1$番目の全経由点を削除する．
Shortcutによる最終的な経路は下図のようになる．
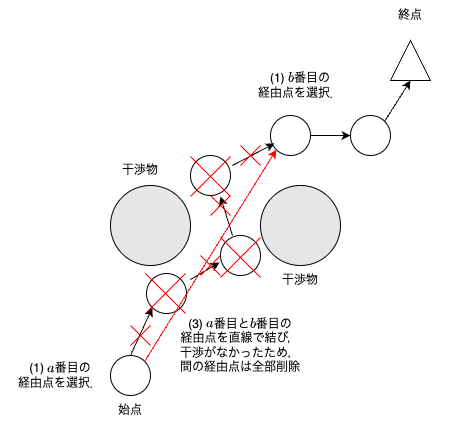
Shortcutを実施することで，環境に依存するが経由点数を減らすことができる．
Shortcutはランダムで経由点を選択するため，Shortcut前の経路が同じであっても，Shortcut後の経路は異なる．ランダムで経由点を選択するため，Shortcut後の経路が最適な経路であるとは限らない．
Partial Shortcutアルゴリズム
Partial Shortcutのアルゴリズムを説明する．
参考文献に記載されているPartial Shortcutのアルゴリズムを抜粋して，下記に記す．
上記アルゴリズムを説明する．
$\prod$は，経路を指す．
$2$行目の$f \leftarrow$ a random degree of freedom は，自由度からランダムで特定の要素を選択して，$f$に代入する．本記事では，経路は2次元$(x, y)$であるため，自由度も$2$である．$f$は$x$または$y$が選択される．
$3$行目の$n \leftarrow |\prod|$は，経由点数である．
$4$行目の$a, b \leftarrow $two random indices $0 \leq a + 1 < b < n$は，$a$と$b$をランダムで選択するが，制約条件も存在する．$a$と$b$が同じ経由点または隣接した経由点を選択しないように制約条件が存在する．
$8$行目の$m \leftarrow |\prod''|$は，経路内の$\pi_{a}$要素と$\pi_{b}$要素内の経由点数を$m$に代入している．$m$には$\pi_{a}$要素と$\pi_{b}$要素の経由点を含んでいる．
$9$行目の for all $\pi_{i}'' \in \prod''$ doは，経路内の$\pi_{a}$要素と$\pi_{b}$要素内の全経由点ループしている．
$10$行目の$\pi_{i}''[f] \leftarrow $INTERPOLATE$(\pi_{0}''[f], \pi_{m-1}''[f], i/(m - 1))$は，経路内の$\pi_{a}$要素と$\pi_{b}$要素内の全経由点の$f$要素を$\pi_{a}$要素と$\pi_{b}$の$f$要素の線形補間(INTERPOLATE)で置き換える．
$12$行目の$\prod'' \in C_{free}$は，$10$行目で置き換えた経路が干渉なければ，$13$行目を自死する．干渉があれば，$loop$の先頭に戻る．
$13$行目の$\prod \leftarrow \prod' \cup \prod'' \cup \prod'''$は経路内の$\pi_{a}$要素と$\pi_{b}$要素内の全経由点を，$10$行目で置き換えた$\prod''$に変更する．
Partial Shortcutの最大回数分ループする．
Partial ShortcutはRRTで作成した経路から2点をランダムに選択していき，選択した経由点間のある要素を直線補間で置き換え，干渉がなければ選択した経由点間の全経由点を直線補間に置き換えるアルゴリズムである．
Partial Shortcutは下図のようなアルゴリズムである．
下図はRRTで作成した経路である．
$a$，$b$番目の経由点と自由度から修正したい要素(図では$x$座標)を選択して，選択した経由点間の$x$座標を直線補間する．
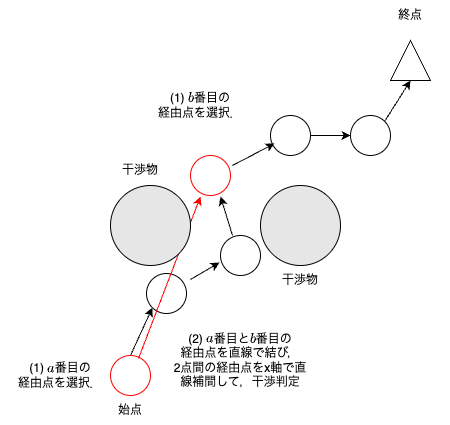
直線補間した$a$番目から$b$番目の全経由点間で干渉ありなら，何もしない(経路は変わらない)．
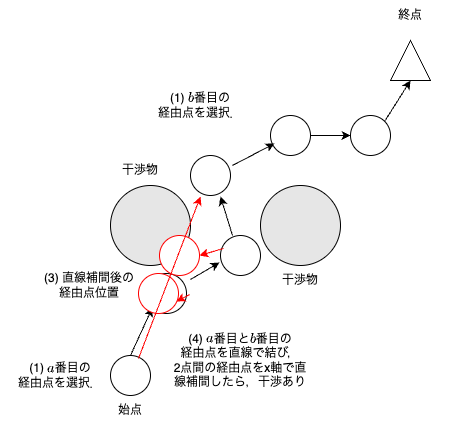
直線補間した$a$番目から$b$番目の全経由点間で干渉なしなら，経路内の$a$番目から$b$番目の全経由点を直線補間した経由点に置き換える．
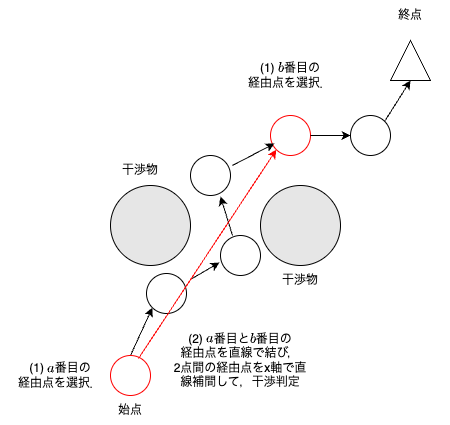
Partial Shortcutによる最終的な経路は下図のようになる．
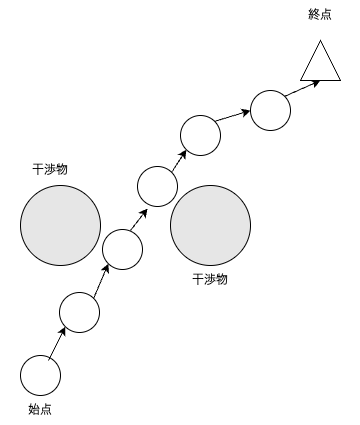
Partial Shortcutを実施することで，経路はスムーズになるが，経由点数は変わらない．
経由点数を減らすためには，Partial Shortcut後の経路に対して，Pruningなどを実施した方が良いかもしれない．
RRT*-Smart アルゴリズム
RRT*-Smart のアルゴリズムを説明する．
参考文献に記載されている RRT*-Smart のアルゴリズムを抜粋して，下記に記す．
RRT* との差異を赤枠で記載した．
各赤枠内の内容を説明する．
赤枠①：
4行目では一定回数(if条件成立時)で，サンプリング手法を変更する．Intelligent Sampling(効率化した探索範囲内でのサンプリング)というサンプリング手法を実装する．Intelligent Samplingに関しては後ほど詳細を説明するが，簡単に言うと$z_{beacons}$を中心とした球内を探索範囲とするサンプリング手法である．4行目のnやbに関しても後ほど説明する．
6行目のelseの場合は，RRT*と同様のランダムサンプリングを実装する．
赤枠②：
15行目では始点から終点までの経路生成に初めて成功したら，16行目でnにiを代入する．要するにnは始点から終点までの経路生成に初めて成功した探索回数が保存される．
17行目ではPath Optimization(経路最適化)と呼ばれる手法を実装して，ツリーの更新および始点から終点までの経路の最小コストを取得する．Path Optimizationに関しては後ほど詳細を説明するが，簡単に言うとあるノードの親ノードをあるノードの親ノードの親ノードに修正して，経路を最適化する手法である．
18行目では始点から終点までの経路の最小コストが以前の最小コストよりも小さければ，19行目のPath Optimization(経路最適化)を実装して，Intelligent Samplingで使用する$z_{beacons}$を計算する．
RRT*-Smart は始点から終点までの経路が初めて生成できるまでは，RRT* と同様の処理を実装する．初めて経路が生成できたら，一定回数でIntelligent Sampling，Path Optimizationを実装する．始点から終点までの最小コストが以前よりも小さくなれば，Intelligent Samplingで使用する$z_{beacons}$を更新する．
RRT*-Smart は下図のようなアルゴリズムである．
上図まではRRT* アルゴリズムである．
下図からは始点から終点までの経路が初めて生成できた後の処理であり，RRT*-Smart 特有アルゴリズムである．
Intelligent SamplingやPath Optimizationに関しての詳細に関しては，次で説明する．
RRT*-Smart のおおまかなアルゴリズムは上図の通りとなる．
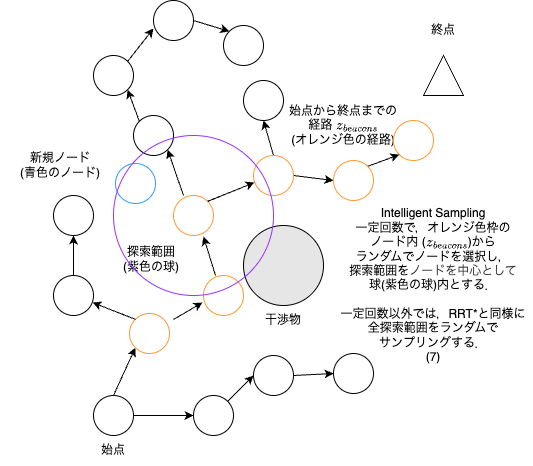
Intelligent Sampling
Intelligent Sampling について説明する．
Intelligent Sampling はサンプリングする時の探索範囲を効率的にするための手法である．
RRT* でのサンプリングは，全探索範囲の中をランダムで探索している．
Intelligent Sampling は$z_{beacons}$と呼ばれる，複数の経由点から1点を選択して，選択した点を中心点として，半径$R_{beacons}$の球内をサンプリングする．
ここで，$z_{beacons}$は始点から終点までの経路の内，最小コストとなる経路の経由点(始点・終点を除く)を指している．
ここからは，複数の経由点が保存されている$z_{beacons}$から，1点を選択する方法および球の半径$R_{beacons}$を決める方法を説明する．
z_{beacons}から1点を選択する方法
複数の経由点が保存されている$z_{beacons}$から，1点を選択する方法を説明する．
案としては下表の3点が挙げられる．
| 案 | 概要 | メリット | デメリット |
|---|---|---|---|
| 1 | ランダム | 選択する点の偏りが少ない | 効率的ではない |
| 2 | 干渉物に近い点 | 干渉物近傍を最適化できる | 選択する点の偏りが大きい |
| 3 | ランダム + 干渉物に近い点(探索回数が多くなるほど干渉物に近い点を選択する確率を高くする) | 選択する点の偏りが少なく，干渉物近傍も最適化できる | 確率の調整が困難 |
上表より本記事では，案3を採用する．
下式のような確率でランダムおよび干渉物に近い点を選択する．
\displaylines{
p = min(0.8, 0.002 * (i - n) \\
p ... 干渉物に近い点を選択する確率 \\
1 - p ... ランダムで選択する確率 \\
i ... RRT*-Smart の探索回数 \\
n ... 始点から終点までの経路生成に成功した時の探索回数 \\
}
初めのうちは$p$が小さいため，ランダムで選択する確率は高くなる．
探索回数を増やしていくと$p$が大きくなるため，干渉物に近い点を選択する確率は高くなる．
次に，干渉物に近い点をどうやって計算するかについて説明する．
python-fcl(干渉判定用ライブラリ)を使用して，干渉物との距離を計算する．python-fclに干渉物との距離を計算できるメソッドがあるため，使用する．
python-fclの使用方法は，下記リンクに記載した．
(python-fclのリンク https://qiita.com/haruhiro1020/items/d364e4c56b1570e1423a)
球の半径$R_{beacons}$を決める方法
球の半径$R_{beacons}$を決める方法を説明する．
案としては下表の3点が挙げられる．
| 案 | 概要 | メリット | デメリット |
|---|---|---|---|
| 1 | 小さい値の固定値 | 局所的な改善ができる | 環境の大きさに応じて，毎回手動で修正 |
| 2 | 始点から終点までの経路コスト * 係数(0.2程度) | 半径が自動で修正 | 経路コストが変わらないときは固定値 |
| 3 | 始点から終点までの経路コスト * 係数(0.2程度) * (1 - min(0.5, (i - n) * 0.001)) | 探索回数が増えると半径が自動で小さくなる | パラメータ調整が困難 |
上表より本記事では，案3を採用する(案3の$i$は探索回数で，$n$は始点から終点までの経路が初めて生成できた探索回数である)．
これらより，Intelligent Sampling を実装していく．
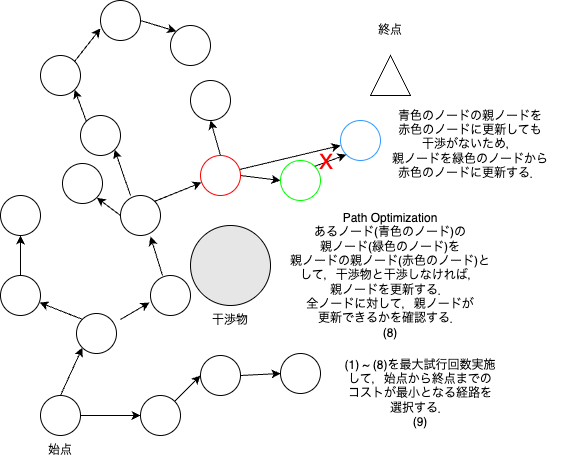
Path Optimization
Path Optimization について説明する．
Path Optimization は経路を最適化するための手法である．
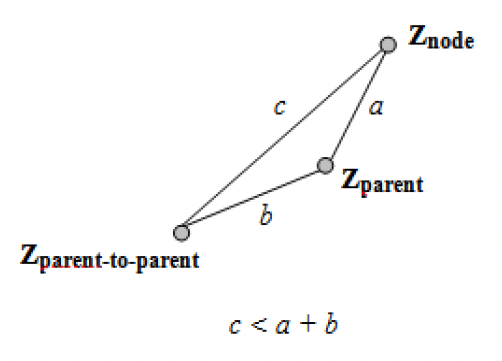
手法およびアルゴリズムを論文から抜粋したのが，下図である．
あるノード$z_{node}$の親ノード($z_{parent}$)を親ノードの親ノード($z_{parent-to-parent}$)にしても干渉がなければ，親ノードを修正するアルゴリズムである．
これを全ノードに対して，実装するのがPath Optimization である．
RRT*-Connect アルゴリズム
RRT*-Connect のアルゴリズムを説明する．
RRT*-Connect は RRT-Connect と同様に始点と終点の双方向から探索し， RRT* ど同様に新規ノードを追加したら，コスト(距離)が最小となるように親ノードを選択する手法である．要するに RRT-Connect の探索回数削減と RRT* の最適性を組み合わせた手法となる．
RRT*-Connect は下図のようなアルゴリズムである．
上図のRRT-Connectアルゴリズムより，状態遷移図を作成した．状態としては，下図の通りになる．
経路生成に関する記事の概要およびリンクと将来作成したい記事
私が作成した経路生成に関する記事の概要およびリンクを下表にまとめる．
将来作成したい記事を下表にまとめる．
| 将来作成したい記事の内容 |
|---|
| 3次元空間で球以外の干渉物が存在する経路生成 (Informed RRT*) |
| 上表以外の経路生成手法 |
| 様々な経路生成手法の比較および組み合わせ |
おわりに
本記事では，経路生成手法の自作記事をまとめた
次記事では，下記内容を実装していきます．
・本記事の"将来作成したい記事"に記載した記事を作成する
・ロボットアームに関する記事を作成する
(https://qiita.com/haruhiro1020/items/47efa3f201f6931ff26b)
・機械学習に関する記事を作成する