はじめに
私がロボットに関して興味を持っており,ロボットの経路を作成したいと思ったところ,RRT* (Rapidly-exploring Random Tree) と呼ばれる経路生成の手法に辿り着いた.
本記事では,経路生成の古典的手法である RRT* (Rapidly-exploring Random Tree) をPythonより,実装してみる.
前記事では,球の干渉物が存在する3次元空間を探索するRRT-Connectを実装した.
前記事の内容を下記に記します.
・https://qiita.com/haruhiro1020/items/74ed385c068d4268f4d5
本記事では,円形の干渉物が存在する2次元空間を探索する RRT* を実装する.
記事に数式を記述する際に下記を参考にした.
・https://qiita.com/PlanetMeron/items/63ac58898541cbe81ada
記事に表を記述する際に下記を参考にした.
・https://qiita.com/zakuroishikuro/items/f33929eab9d55c5bd073
RRTは下記を参考にした.
・https://dronevisionml.blogspot.com/2016/11/rrt.html
・https://developers.agirobots.com/jp/rapidly-exploring-random-tree-star/
・https://myenigma.hatenablog.com/entry/2017/05/07/022346
参考文献:
S.Karaman, E.Frazzoli "Incremental Sampling-based Algorithms for Optimal Motion Planning.", arXiv 2010.
RRT* はRRTに最適性を付与したアルゴリズムである.RRTとRRT* の違いは後ほど説明する.
本記事で実装すること
・円形の干渉物が存在する2次元空間でのRRT* による経路生成
・RRTとRRT* の経路生成結果をグラフで表現する
本記事では実装できないこと(将来実装したい内容)
・球の干渉物が存在する3次元空間でのRRT* による経路生成
・RRT* の経路生成の過程をアニメーション化する
動作環境
・macOS Sequoia (バージョン15.5)
・Python3 (3.10.9)
・Numpy (1.23.5) (数値計算用ライブラリ)
・Matplotlib (3.7.0) (アニメーション作成用ライブラリ)
経路生成手法のまとめ
経路生成手法をまとめた記事を展開いたします.RRT以外の手法も記載してますので,参照いただけますと幸いです.
(https://qiita.com/haruhiro1020/items/000b3287fce082ae4283)
RRTに関して
RRTに関して説明する.
参考文献に記載されているRRTのアルゴリズムを抜粋して,下記に記す.
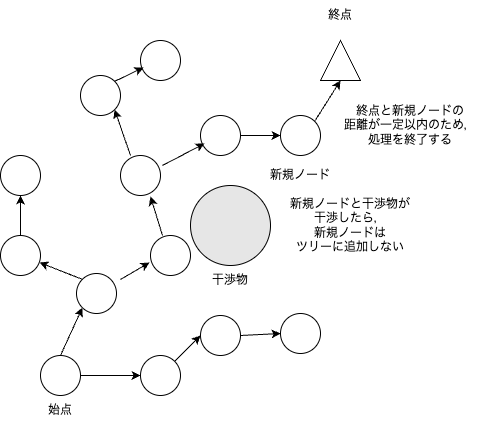
RRTは始点から,終点に向かってどんどんノードを増やしていき,終点との距離がある値以下になったら,経路生成を完了する.
RRTは下図のようなアルゴリズムである.
RRT* に関して
RRT* に関して説明する.
参考文献に記載されているRRT* のアルゴリズムを抜粋して,下記に記す.
RRTとの差異を赤枠で記載した.
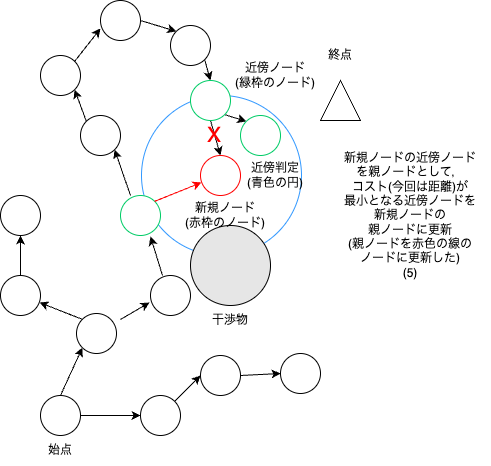
RRT* は始点から,終点に向かってどんどんノードを増やしていき,新規ノードの周辺ノードでコストが最小となるように,親ノードを修正していく.
一定回数実行後に,始点から終点までのコストが最小となる経路を選択する
RRT* は下図のようなアルゴリズムである.
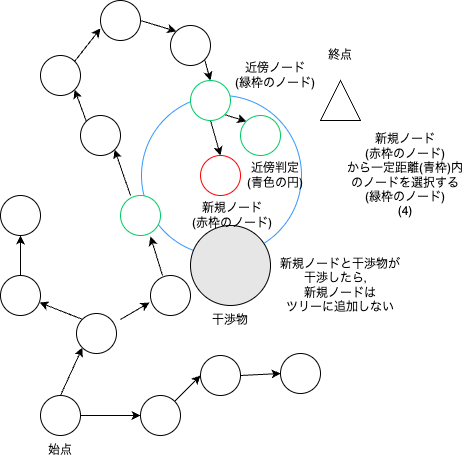
新規ノードを作成した時の近傍ノードを探索する範囲は以下のように定義されている.
\displaylines{
r = R * (\log N / N)^{1/d} \\
r ... 近傍ノードの探索範囲 \\
N ... ツリー内のノード数 \\
d ... 探索空間の次元数 \\
R ... ハイパーパラメータ \\
}
ノード数(N)が多い(探索の試行回数が多い)ほど,近傍ノードの探索範囲(r)は小さくなる.
ハイパーパラメータであるRの値を決めるのが困難である.
Rの値が大きい時のメリット・デメリットは以下の通りである.
メリット
・近傍ノードの数が増えるため,コストが最小となる経路を算出しやすい
デメリット
・処理時間が増える
後ほど,RRT* の経路生成結果のグラフを提示することで,ハイパーパラメータRの値による経路生成結果への影響を説明する.
RRTとRRT* との差異
上でRRTとRRT* を説明した.
ここでは,RRTとRRT* で 同じ/異なる 内容を説明する.
RRTとRRT* で同様な内容
・ランダムな点を取る
・ランダムな点とツリー内の最短ノードを計算し,新規ノードを作成する
・最短ノードと新規ノード間での干渉チェック
RRTとRRT* で異なる内容
・新規ノードの親ノードは近傍ノードからコストが最小となるノードを採用する
・新規ノードを採用したら,近傍ノードの親ノードを新規ノードと仮置きして,コストが下がれば,親ノードを新規ノードとして採用する
RRTでは,新規ノードが乱数に影響するため,最適な経路が保証されない.
RRT* では,新規ノードを乱数で作成するが,コスト(今回は距離)が最小となるように親ノードも更新するため,最適な経路になりやすい.(試行回数を無限にすると,最適な経路になるが,実装時は試行回数を有限とするため,必ず最適な経路になるとは限らない)
RRT* は,コストが最小となるように親ノードを更新する処理が増えるため,RRTに比べると処理時間が増加する.
始点から終点までの経路生成(円形の干渉物が存在する2次元空間)
Pythonによる RRT/RRT-Connect/RRT* の実装は下記の通りです.
# 複数ファイルで使用する定数の定義
# RRT-Connectの状態を定義
STATE_START_TREE_RANDOM = 0 # 始点ツリーにランダム点を追加
STATE_START_TREE_END_TREE = 1 # 始点ツリーから終点ツリーへノードを伸ばす
STATE_END_TREE_RANDOM = 2 # 終点ツリーにランダム点を追加
STATE_END_TREE_START_TREE = 3 # 終点ツリーから始点ツリーへノードを伸ばす
# 経路生成アルゴリズムを定義
PATH_PLANNING_RRT = 10 # RRTによる経路生成
PATH_PLANNING_RRT_CONNECT = 11 # RRT-Connectによる経路生成
PATH_PLANNING_RRT_STAR = 12 # RRT*による経路生成
# ノードの最短ノード要素とコスト要素を定義
RRT_NEAR_NODE_IDX = -1 # RRTでの最短ノード要素
RRT_CONNECT_NEAR_NODE_IDX = -1 # RRT-Connectでの最短ノード要素
RRT_STAR_NEAR_NODE_IDX = -3 # RRT*での最短ノード勝訴
RRT_STAR_COST_IDX = -2 # RRT*でのコスト要素
RRT_STAR_RADIUS_IDX = -1 # RRT*での半径要素
# 次元数を定義
DIMENTION_2D = 2 # 2次元
DIMENTION_3D = 3 # 3次元
# ツリーの初期ノードの親ノード
INITIAL_NODE_NEAR_NODE = -1 # 初期ノードに親ノードが存在しないから-1
# プロットする時にグラフ(静止画)とするかアニメーションを定義
PLOT_NONE = 20 # プロットしない
PLOT_GRAPH = 21 # グラフ
PLOT_ANIMATION = 22 # アニメーション
# 経路生成手法であるRRT (Rapidly-exploring Random Tree) の実装
# ライブラリの読み込み
import numpy as np
import time
import os
# 自作モジュールの読み込み
from constant import *
class RRT:
"""
RRTクラス
プロパティ
_pathes(numpy.ndarray): 始点から終点までの経路
_debug_pathes(numpy.ndarray): デバッグ用経路
_debug_random_pathes(numpy.ndarray): デバッグ用ランダム位置
_strict_min_pos(numpy.ndarray): 探索の最小範囲
_strict_max_pos(numpy.ndarray): 探索の最大範囲
_interference_obj(list): 干渉物
publicメソッド (全てのクラスから参照可能)
planning(): 経路生成の実装
pathes(): _pathesプロパティのゲッター
debug_pathes(): _debug_pathesプロパティのゲッター
debug_random_pathes(): _debug_random_pathesプロパティのゲッター
strict_min_pos(): _strict_min_posプロパティのゲッター
strict_max_pos(): _strict_max_posプロパティのゲッター
interference_obj(): _interference_objプロパティのゲッター
protectedメソッド (自クラスまたは子クラスが参照可能)
_reset(): データの初期化
_set_node(): データにノードを設定する
_chk_end_pos_dist(): 終点との距離が一定範囲内であるかの確認
_fin_planning(): 経路生成の終了処理
_calc_new_pos(): 最短ノードからランダムな値方向へ新しいノード(位置)を作成
_get_near_node(): ランダムな位置と最短距離であるノードを取得
_strict_planning_pos(): 探索範囲を制限する
_get_random_pos(): ランダムな位置を取得
_set_interference_obj(): 干渉物を設定
_is_interference_pos(): 干渉判定処理
"""
# 定数の定義
_MOVING_VALUE = 0.25 # 1回の移動量
_STRICT_PLANNING_POS = 0.2 # 探索範囲の制限
_TIMEOUT_VALUE = 10 # タイムアウト時間 [second]
_FILE_NAME_PATHES = "pathes.csv" # _pathesプロパティを保存するファイル名
_FILE_NAME_DEBUG_PATHES = "debug_pathes.csv" # _debug_pathesプロパティを保存するファイル名
_FILE_NAME_DEBUG_RANDOM_PATHES = "debug_random_pathes.csv" # _debug_random_pathesプロパティを保存するファイル名
_NODE_RADIUS = 0.05 # ノードの半径
_NODE_NEAR_NODE_IDX = RRT_NEAR_NODE_IDX # ノード内の最短ノード要素
_GOAL_SAMPLE_RATE = 0.0 # ランダムな値を取るときに,終点を選択する確率
_DEVIDED_DISTANCE = 0.05 # 2点間を分割する際の基準距離
def __init__(self):
"""
コンストラクタ
"""
self._debug_pathes = []
self._debug_random_pathes = []
self._pathes = []
self._interference_obj = []
@property
def pathes(self):
"""
_pathesプロパティのゲッター
"""
return self._pathes
@property
def debug_pathes(self):
"""
_debug_pathesプロパティのゲッター
"""
return self._debug_pathes
@property
def debug_random_pathes(self):
"""
_debug_random_pathesプロパティのゲッター
"""
return self._debug_random_pathes
@property
def strict_min_pos(self):
"""
_strict_min_posプロパティのゲッター
"""
return self._strict_min_pos
@property
def strict_max_pos(self):
"""
_strict_max_posプロパティのゲッター
"""
return self._strict_max_pos
@property
def interference_obj(self):
"""
_interference_objプロパティのゲッター
"""
return self._interference_obj
def _set_interference_obj(self, interference_obj):
"""
干渉物を設定
パラメータ
interference_obj(list): 干渉物
戻り値
set_result(bool): True / False = 設定の成功 / 失敗
"""
set_result = True
if interference_obj:
# 干渉物が存在する
# 干渉物と始点/終点の次元数が一致しているかの確認 (# 変更 ↓)
for interference in interference_obj:
if self._dim != interference.dimention:
# 不一致
set_result = False
break
if set_result:
self._interference_obj = interference_obj
# 変更 ↑
else:
self._interference_obj = []
return set_result
def _set_node(self, node):
"""
データにノードを設定する
パラメータ
node(numpy.ndarray): ノード位置と最短距離ノード番号 (最終要素)
"""
if len(self._debug_pathes) == 0:
self._debug_pathes = node
else:
self._debug_pathes = np.append(self._debug_pathes, node, axis=0)
def _set_random_node(self, node):
"""
データにノードを設定する
パラメータ
node(numpy.ndarray): ノード位置と最短距離ノード番号 (最終要素)
"""
if len(self._debug_random_pathes) == 0:
self._debug_random_pathes = node
else:
self._debug_random_pathes = np.append(self._debug_random_pathes, node, axis=0)
def planning(self, start_pos, end_pos, interference_obj):
"""
経路生成
パラメータ
start_pos(numpy.ndarray): 経路生成の始点
end_pos(numpy.ndarray): 経路生成の終点
interference_obj(list): 干渉物
戻り値
result(bool): True / False = 成功 / 失敗
"""
# 処理結果
result = False
# 始点と終点の次元数が一致しているかの確認
start_pos_dim = np.size(start_pos)
end_pos_dim = np.size(end_pos)
if start_pos_dim != end_pos_dim:
# 次元数が異なるので異常
return result
self._dim = start_pos_dim
# 干渉物を設定
if not self._set_interference_obj(interference_obj):
# 干渉物と始点/終点の次元数が不一致のため,処理失敗
return result
# 始点ノードを設定
self._set_node(np.append(start_pos, INITIAL_NODE_NEAR_NODE).reshape(1, -1))
self._set_random_node(np.append(start_pos, INITIAL_NODE_NEAR_NODE).reshape(1, -1))
# 探索する範囲を設定
self._strict_planning_pos(start_pos, end_pos)
# 経路生成は一定時間内に終了させる
start_time = time.time()
# 終点までの経路生成が終わるまでループ
while True:
# ランダムな値を取得
random_pos = self._get_random_pos(end_pos)
# ランダムな値と最短ノードを計算
near_node = self._get_near_node(random_pos)
# 最短ノード位置を取得
near_pos = self._debug_pathes[near_node, :self._NODE_NEAR_NODE_IDX]
# 最短ノードからランダムな値方向へ新しいノード(位置)を作成
new_pos = self._calc_new_pos(random_pos, near_pos)
# 新規ノードと最短ノード間での干渉判定
is_interference = self._line_interference(new_pos, near_pos)
if not is_interference:
# 干渉なしのため,データを設定する
# ランダムノードを設定
self._set_random_node(np.append(random_pos, near_node).reshape(1, -1))
# ノードを設定
self._set_node(np.append(new_pos, near_node).reshape(1, -1))
# 終点との距離が一定範囲内であるかの確認
if self._chk_end_pos_dist(new_pos, end_pos):
# 一定範囲内のため,経路生成の完了
result = True
break
# 干渉の有無に関わらずにタイムアウトの確認はする
now_time = time.time()
if now_time - start_time >= self._TIMEOUT_VALUE:
# タイムアウト
break
if result:
# 経路生成に成功のため,経路生成の終了処理
self._fin_planning(start_pos, end_pos)
return result
def _is_interference_pos(self, pos):
"""
干渉判定処理
パラメータ
pos(numpy.ndarray): 干渉判定したい点
戻り値
is_interference(bool): True / False = 干渉あり / なし
"""
is_interference = False
for interference in self._interference_obj:
if self._dim == DIMENTION_2D:
# RRTで生成した点は円形と仮定して,干渉判定
if interference.is_interference_circle(pos, self._NODE_RADIUS):
# 干渉あり
is_interference = True
break
else:
# RRTで生成した点は球と仮定して,干渉判定
if interference.is_interference_ball(pos, self._NODE_RADIUS):
# 干渉あり
is_interference = True
break
return is_interference
def _chk_end_pos_dist(self, pos, end_pos):
"""
終点との距離が一定範囲内であるかの確認
パラメータ
pos(numpy.ndarray): ノード位置
end_pos(numpy.ndarray): 経路生成の終点
戻り値
is_near(bool): True / False = 一定範囲内である / でない
"""
is_near = False
# 距離を計算
dist = np.linalg.norm(end_pos - pos)
# 一定範囲内であるかの確認
if dist <= self._MOVING_VALUE:
is_near = True
return is_near
def _fin_planning(self, start_pos, end_pos):
"""
経路生成の終了処理
パラメータ
start_pos(list): 経路生成の始点
end_pos(list): 経路生成の終点
"""
# 始点から終点までの経路に関係するノードを選択
revers_path = end_pos
near_node = -1
while True:
# 終点から始点方向へノードを取得
node = self._debug_pathes[near_node, :]
pos = node[:self._NODE_NEAR_NODE_IDX].reshape(1, -1)
# 浮動小数型になっているので,整数型に型変換
near_node = int(node[self._NODE_NEAR_NODE_IDX])
revers_path = np.append(revers_path, pos, axis=0)
if near_node == INITIAL_NODE_NEAR_NODE:
# 始点ノードまで取得できたため,処理終了
break
# 経路が終点からの順番になっているため,始点から終点とする
self._pathes = revers_path[::-1]
# デバッグ用の経路に終点を追加
self._set_random_node(np.append(end_pos, self._debug_pathes.shape[0] - 1).reshape(1, -1))
self._set_node(np.append(end_pos, self._debug_pathes.shape[0] - 1).reshape(1, -1))
def _calc_new_pos(self, random_pos, near_pos):
"""
最短ノード(位置)からランダムな値方向へ新しいノード(位置)を作成
パラメータ
random_pos(numpy.ndarray): ランダムな位置
near_pos(numpy.ndarray): 最短ノード位置
戻り値
new_pos(numpy.ndarray): 新しいノード
"""
# 方向を計算
direction = random_pos - near_pos
# 方向の大きさを1にする
norm_direction = direction / np.linalg.norm(direction)
# 新しいノードを作成
new_pos = near_pos + norm_direction * self._MOVING_VALUE
return new_pos
def _get_near_node(self, random_pos):
"""
ランダムな位置との最短距離ノードを取得
パラメータ
random_pos(numpy.ndarray): ランダムな位置
戻り値
min_dist_node(int): 最短距離ノード
"""
# 最後以外に位置が保存されている
node_pos = self._debug_pathes[:, :self._NODE_NEAR_NODE_IDX]
# 差分を計算
difference = node_pos - random_pos
# 差分から距離を計算
distance = np.linalg.norm(difference, axis=1)
# 最小距離のノードを取得
min_dist_node = np.argmin(distance)
return min_dist_node
def _strict_planning_pos(self, start_pos, end_pos):
"""
探索範囲を制限する
パラメータ
start_pos(numpy.ndarray): 始点
end_pos(numpy.ndarray): 終点
"""
all_pos = np.append(start_pos, end_pos, axis=0)
# 各列の最大/最小値を取得
min_pos = np.min(all_pos, axis=0)
max_pos = np.max(all_pos, axis=0)
self._strict_min_pos = min_pos - self._STRICT_PLANNING_POS
self._strict_max_pos = max_pos + self._STRICT_PLANNING_POS
def _get_random_pos(self, end_pos):
"""
ランダムな位置を取得
戻り値
random_pos(numpy.ndarray): ランダムな位置
"""
# ランダムな位置か終点を選択するかの確率
select_goal = np.random.rand()
if select_goal < self._GOAL_SAMPLE_RATE:
# 終点を選択する
random_pos = end_pos
else:
random_pos = np.random.uniform(self._strict_min_pos, self._strict_max_pos)
return random_pos
def _line_interference(self, pos1, pos2):
"""
2点間の干渉チェック
パラメータ
pos1(numpy.ndarray): 位置1
pos2(numpy.ndarray): 位置2
戻り値
is_interference(bool): True / False = 干渉あり / 干渉なし
"""
is_interference = False
# 2点間の距離を算出
difference = pos2 - pos1
distance = np.linalg.norm(difference)
# 2点間の分割数を算出
n_devided = max(int(distance / self._DEVIDED_DISTANCE), 1)
for i in range(n_devided + 1):
direct_pos = i / n_devided * difference
devided_pos = pos1 + direct_pos
if self._is_interference_pos(devided_pos):
# 干渉あり
is_interference = True
break
return is_interference
def save(self):
"""
生成した経路をファイル保存
"""
np.savetxt(self._FILE_NAME_PATHES, self._pathes)
np.savetxt(self._FILE_NAME_DEBUG_PATHES, self._debug_pathes)
np.savetxt(self._FILE_NAME_DEBUG_RANDOM_PATHES, self._debug_random_pathes)
class RRTConnect(RRT):
"""
RRT-Connectクラス
プロパティ
_start_tree(numpy.ndarray): 始点ツリー
_end_tree(numpy.ndarray): 終点ツリー
_state(int): ツリーの状態
_debug_states(list): ツリー状態のデバッグ
publicメソッド (全てのクラスから参照可能)
planning(): 経路生成の実装
start_tree(): _start_treeプロパティのゲッター
end_tree(): _end_treeプロパティのゲッター
debug_states(): _debug_statesプロパティのゲッター
save(): 生成した経路をファイル保存
protectedメソッド (自クラスまたは子クラスが参照可能)
_set_node_start_tree(): 始点ツリーにノードを設定する
_set_node_end_tree(): 終点ツリーにノードを設定する
_fin_planning(): 経路生成の終了処理
_get_near_node(): ランダムな位置と最短距離であるノードを取得
_save_state(): 状態を保存
_state_transition(): 状態を遷移させる
_exec_state(): 状態に応じた処理を実施
"""
# 定数の定義
_FILE_NAME_START_TREE = "start_tree.csv" # _start_treeプロパティを保存するファイル名
_FILE_NAME_END_TREE = "end_tree.csv" # _end_treeプロパティを保存するファイル名
_FILE_NAME_DEBUG_STATES = "debug_states.csv" # _debug_statesプロパティを保存するファイル名
_NODE_NEAR_NODE_IDX = RRT_CONNECT_NEAR_NODE_IDX # ノード内の最短ノード要素
def __init__(self):
"""
コンストラクタ
"""
# 親クラスの初期化
super().__init__()
# プロパティの初期化
self._start_tree = []
self._end_tree = []
self._state = STATE_START_TREE_RANDOM
self._debug_states = []
@property
def start_tree(self):
"""
_start_treeプロパティのゲッター
"""
return self._start_tree
@property
def end_tree(self):
"""
_end_treeプロパティのゲッター
"""
return self._end_tree
@property
def debug_states(self):
"""
_debug_statesプロパティのゲッター
"""
return self._debug_states
def _set_node_start_tree(self, node):
"""
始点ツリーにノードを設定する
パラメータ
node(numpy.ndarray): ノード位置
"""
if len(self._start_tree) == 0:
self._start_tree = node
else:
self._start_tree = np.append(self._start_tree, node, axis=0)
def _set_node_end_tree(self, node):
"""
終点ツリーにノードを設定する
パラメータ
node(numpy.ndarray): ノード位置
"""
if len(self._end_tree) == 0:
self._end_tree = node
else:
self._end_tree = np.append(self._end_tree, node, axis=0)
def planning(self, start_pos, end_pos, interference_obj):
"""
経路生成
パラメータ
start_pos(numpy.ndarray): 経路生成の始点
end_pos(numpy.ndarray): 経路生成の終点
interference_obj(list): 干渉物
戻り値
result(bool): True / False = 成功 / 失敗
"""
# 処理結果
result = False
# 始点と終点の次元数が一致しているかの確認
start_pos_dim = np.size(start_pos)
end_pos_dim = np.size(end_pos)
if start_pos_dim != end_pos_dim:
# 次元数が異なるので異常
return result
self._dim = start_pos_dim
# 干渉物を設定
if not self._set_interference_obj(interference_obj):
# 干渉物と始点/終点の次元数が不一致のため,処理失敗
return result
# 始点ツリーに始点ノードを設定
self._set_node_start_tree(np.append(start_pos, INITIAL_NODE_NEAR_NODE).reshape(1, -1))
# 終点ツリーに終点のーどを設定
self._set_node_end_tree(np.append(end_pos, INITIAL_NODE_NEAR_NODE).reshape(1, -1))
# 探索する範囲を設定
self._strict_planning_pos(start_pos, end_pos)
# 経路生成は一定時間内に終了させる
start_time = time.time()
# 始点から終点までの経路生成が終わるまでループ
while True:
# 1処理実施して,経路生成が完了したか確認する
if self._exec_state(start_pos, end_pos):
# 経路生成の完了
result = True
break
# 干渉の有無に関わらずにタイムアウトの確認はする
now_time = time.time()
if now_time - start_time >= self._TIMEOUT_VALUE:
# タイムアウト
break
if result:
# 経路生成に成功のため,経路生成の終了処理
self._fin_planning(start_pos, end_pos)
return result
def _state_transition(self):
"""
状態を遷移させる
"""
if self._state == STATE_START_TREE_RANDOM: # 始点ツリーにランダム点を追加する状態
self._state = STATE_END_TREE_START_TREE
elif self._state == STATE_START_TREE_END_TREE: # 始点ツリーに終点ツリーで作成したノードへ伸ばす状態
self._state = STATE_START_TREE_RANDOM
elif self._state == STATE_END_TREE_RANDOM: # 終点ツリーにランダム点を追加する状態
self._state = STATE_START_TREE_END_TREE
else: # 終点ツリーに始点ツリーで作成したノードへ伸ばす状態
self._state = STATE_END_TREE_RANDOM
def _save_state(self):
"""
状態を保存
"""
self._debug_states.append(self._state)
def _exec_state(self, start_pos, end_pos):
"""
状態(_state)に応じた処理を実施
パラメータ
start_pos(numpy.ndarray): 始点
end_pos(numpy.ndarray): 終点
戻り値
complete_path(bool): True / False = 経路生成の完了 / 未完了
"""
complete_path = False
# 最短ノードを算出したいツリーを取得
if self._state == STATE_START_TREE_RANDOM or self._state == STATE_START_TREE_END_TREE:
# 始点ツリーにランダム点を追加する状態または始点ツリーに終点ツリーで作成したノードへ伸ばす状態
my_tree = self._start_tree
your_tree = self._end_tree
set_tree_func = self._set_node_start_tree
target_pos = end_pos
else:
my_tree = self._end_tree
your_tree = self._start_tree
set_tree_func = self._set_node_end_tree
target_pos = start_pos
# ツリーにランダム点を追加
if self._state == STATE_START_TREE_RANDOM or self._state == STATE_END_TREE_RANDOM:
# 始点ツリーにランダム点を追加する状態または終点ツリーにランダム点を追加する状態
# ランダムな値を取得する
random_pos = self._get_random_pos(target_pos)
# ランダムな値とツリーの最短ノードを計算
near_node = self._get_near_node(random_pos, my_tree)
# 位置と最短ノードが保存されているから,位置だけを取得
near_pos = my_tree[near_node][:-1]
# 最短ノードからランダムな値方向へ新しいノードを作成
new_pos = self._calc_new_pos(random_pos, near_pos)
# 新規ノードと最短ノード間での干渉判定
is_interference = self._line_interference(new_pos, near_pos)
if not is_interference:
# ツリーにノードを追加
set_tree_func(np.append(new_pos, near_node).reshape(1, -1))
# 状態を保存
self._save_state()
# 干渉なしのため,状態を遷移させる
self._state_transition()
else:
# ツリーで作成したノードを取得
end_pos = your_tree[-1, :self._NODE_NEAR_NODE_IDX]
# ツリー内の最短ノードを計算
near_node = self._get_near_node(end_pos, my_tree)
# 位置と最短ノードが保存されているから,位置だけを取得
near_pos = my_tree[near_node, :self._NODE_NEAR_NODE_IDX]
# 最短ノードから終点ツリーのノード方向へ新しいノードを作成
new_pos = self._calc_new_pos(end_pos, near_pos)
# 干渉物との干渉判定
is_interference = self._line_interference(new_pos, near_pos)
if is_interference:
# 干渉ありのため,状態を遷移させる
self._state_transition()
else:
# ツリーにノードを追加
set_tree_func(np.append(new_pos, near_node).reshape(1, -1))
# 状態を保存
self._save_state()
# 始点から終点までの経路が生成できたかの確認
if self._chk_end_pos_dist(new_pos, end_pos):
# 経路生成の完了
complete_path = True
return complete_path
def _fin_planning(self, start_pos, end_pos):
"""
経路生成の終了処理
パラメータ
start_pos(list): 経路生成の始点
end_pos(list): 経路生成の終点
"""
# 始点ツリーから,終点ツリーと繋がったパスを取得
start_path = []
near_node = -1
while True:
# 終点ツリーと繋がったノードから始点へノードを取得
node = self._start_tree[near_node, :]
pos = node[:self._NODE_NEAR_NODE_IDX].reshape(1, -1)
# 浮動小数型になっているので,整数型に型変換
near_node = int(node[self._NODE_NEAR_NODE_IDX])
if len(start_path) == 0:
# 初回の場合
start_path = pos
else:
start_path = np.append(start_path, pos, axis=0)
if near_node == INITIAL_NODE_NEAR_NODE:
# 始点ノードまで取得できたため,ループ終了
break
# 始点ツリーのパスは,逆順(終点ツリーと繋がったノードから始点ノードの順番)に保存されているから,正順に変更
self._pathes = start_path[::-1]
# 終点ツリーから,始点ツリーと繋がったパスを取得
end_path = []
near_node = -1
while True:
# 始点ツリーと繋がったノードから終点へノードを取得
node = self._end_tree[near_node, :]
pos = node[:self._NODE_NEAR_NODE_IDX].reshape(1, -1)
# 浮動小数型になっているので,整数型に型変換
near_node = int(node[self._NODE_NEAR_NODE_IDX])
if len(end_path) == 0:
# 初回の場合
end_path = pos
else:
end_path = np.append(end_path, pos, axis=0)
if near_node == INITIAL_NODE_NEAR_NODE:
# 終点ノードまで取得できたため,ループ終了
break
# 始点から終点までの経路を保存
self._pathes = np.append(self._pathes, end_path, axis=0)
def _get_near_node(self, random_pos, tree):
"""
ランダムな位置とツリーの最短距離ノードを取得
パラメータ
random_pos(numpy.ndarray): ランダムな位置
tree(numpy.ndarray): ツリー
戻り値
min_dist_node(int): 最短距離ノード
"""
# 最後以外に位置が保存されている
node_pos = tree[:, :self._NODE_NEAR_NODE_IDX]
# 差分を計算
difference = node_pos - random_pos
# 差分から距離を計算
distance = np.linalg.norm(difference, axis=1)
# 最小距離のノードを取得
min_dist_node = np.argmin(distance)
return min_dist_node
def save(self):
"""
生成した経路をファイル保存
"""
np.savetxt(self._FILE_NAME_PATHES, self._pathes)
np.savetxt(self._FILE_NAME_START_TREE, self._start_tree)
np.savetxt(self._FILE_NAME_END_TREE, self._end_tree)
np.savetxt(self._FILE_NAME_DEBUG_STATES, self._debug_states)
class RRTStar(RRT):
"""
RRT*クラス
プロパティ
_pathes(numpy.ndarray): 始点から終点までの経路
_debug_pathes(numpy.ndarray): デバッグ用経路
_debug_random_pathes(numpy.ndarray): デバッグ用ランダム位置
_strict_min_pos(numpy.ndarray): 探索の最小範囲
_strict_max_pos(numpy.ndarray): 探索の最大範囲
_interference_obj(list): 干渉物
_max_iterate(int): 最大探索回数
_count_success(int): ノード追加の成功回数
_near_node_radius(float): 近傍ノードの探索半径
publicメソッド (全てのクラスから参照可能)
planning(): 経路生成の実装
count_success(int): _count_successプロパティのゲッター
protectedメソッド (自クラスまたは子クラスが参照可能)
_calc_cost(): コストの計算
_get_near_node_list(): ノードと近傍ノードをリストで取得
_get_min_cost_node(): コストが最小となる近傍ノードを取得
_update_near_node(): 近傍ノード内の親ノードを更新
_fin_planning(): 経路生成の終了処理
_save_current_tree(): 現在のツリーをファイル化
"""
# 定数の定義
_FILE_NAME_PATHES = "rrt_star_pathes.csv" # _pathesプロパティを保存するファイル名
_FILE_NAME_DEBUG_PATHES = "rrt_star_debug_pathes.csv" # _debug_pathesプロパティを保存するファイル名
_FILE_NAME_DEBUG_RANDOM_PATHES = "rrt_star_debug_random_pathes.csv" # _debug_random_pathesプロパティを保存するファイル名
_MAX_ITERATE = 200 # 最大探索回数
_NODE_NEAR_NODE_IDX = RRT_STAR_NEAR_NODE_IDX # ノード内の最短ノード要素
_NODE_COST_IDX = RRT_STAR_COST_IDX # ノード内のコスト要素
_TIMEOUT_VALUE = 1000 # タイムアウト時間 [second]
_FOLDER_NAME_CURRENT_TREE = "result" # ノード追加時の現在のツリーを保存するフォルダ名
_FILE_NAME_CURRENT_TREE = "rrt_start_current_tree" # ノード追加時の現在のツリーを保存するファイル名
def __init__(self):
"""
コンストラクタ
"""
# 親クラスの初期化処理
super().__init__()
self._max_iterate = self._MAX_ITERATE
# フォルダを作成しておく (存在済みの場合はエラーを発生させない(引数 exist_ok をTrueとする))
os.makedirs(self._FOLDER_NAME_CURRENT_TREE, exist_ok=True)
self._near_node_radius = self._MOVING_VALUE * 20
@property
def max_iterate(self):
"""
_max_iterateプロパティのゲッター
"""
return self._max_iterate
@max_iterate.setter
def max_iterate(self, value):
"""
_max_iterateプロパティのセッター
パラメータ
value(int): 設定したい値
"""
# 負の値では何もしない
if value > 0:
self._max_iterate = value
@property
def near_node_radius(self):
"""
_near_node_radiusプロパティのゲッター
"""
return self._near_node_radius
@near_node_radius.setter
def near_node_radius(self, value):
"""
_near_node_radiusプロパティのセッター
パラメータ
value(float): 設定したい値
"""
# 負の値では,何もしない
if value > 0:
self._near_node_radius = value
@property
def count_success(self):
"""
_count_successプロパティのゲッター
"""
return self._count_success
@property
def file_name_current_tree(self):
"""
_FILE_NAME_CURRENT_TREE定数のゲッター
"""
return self._FILE_NAME_CURRENT_TREE
@property
def foler_name_current_tree(self):
"""
_FOLDER_NAME_CURRENT_TREE定数のゲッター
"""
return self._FOLDER_NAME_CURRENT_TREE
def planning(self, start_pos, end_pos, interference_obj):
"""
経路生成
パラメータ
start_pos(numpy.ndarray): 経路生成の始点
end_pos(numpy.ndarray): 経路生成の終点
interference_obj(list): 干渉物
戻り値
result(bool): True / False = 成功 / 失敗
"""
# 処理結果
result = False
# 始点と終点の次元数が一致しているかの確認
start_pos_dim = np.size(start_pos)
end_pos_dim = np.size(end_pos)
if start_pos_dim != end_pos_dim:
# 次元数が異なるので異常
return result
self._dim = start_pos_dim
# 干渉物を設定
if not self._set_interference_obj(interference_obj):
# 干渉物と始点/終点の次元数が不一致のため,処理失敗
return result
# 始点ノードを設定 (# 変更 コストを追加した)
array_data = np.array([INITIAL_NODE_NEAR_NODE, 0.0, 0.0])
self._set_node(np.append(start_pos, array_data).reshape(1, -1))
self._set_random_node(np.append(start_pos, array_data).reshape(1, -1))
# 探索する範囲を設定
self._strict_planning_pos(start_pos, end_pos)
# 経路生成は一定時間内に終了させる
start_time = time.time()
self._count_success = 0 # ノード追加に失敗した回数
# 全探索回数ループ
for i in range(self._max_iterate):
print(f"i = {i}")
# ランダムな値を取得
random_pos = self._get_random_pos(end_pos)
# ランダムな値と最短ノードを計算
near_node = self._get_near_node(random_pos)
# 最短ノード位置を取得
near_pos = self._debug_pathes[near_node, :self._NODE_NEAR_NODE_IDX]
# 最短ノードからランダムな値方向へ新しいノード(位置)を作成
new_pos = self._calc_new_pos(random_pos, near_pos)
# 新しい点と干渉物との干渉判定
is_interference = self._line_interference(new_pos, near_pos)
if not is_interference:
# 干渉なしのため,データを設定する
# 新規箇所 ↓
# 新規ノードのコストを計算
new_cost = self._calc_cost(new_pos, near_node)
# 近傍ノードを全部取得
near_node_list, threshold = self._get_near_node_list(new_pos)
# 近傍ノードからコストが最小となるノードを取得
min_cost_node, min_cost = self._get_min_cost_node(new_pos, near_node_list, near_node, new_cost)
# 近傍ノード内でコストが小さくなれば,最短ノードを更新
self._update_near_node(new_pos, near_node_list, min_cost)
# 新規箇所 ↑
# ランダムノードを設定
array_data = np.array([min_cost_node, min_cost, threshold])
self._set_random_node(np.append(random_pos, array_data).reshape(1, -1))
# ノードを設定
self._set_node(np.append(new_pos, array_data).reshape(1, -1))
# 終点との距離が一定範囲内であるかの確認
if self._chk_end_pos_dist(new_pos, end_pos):
# 一定範囲内のため,戻り値を成功に更新
result = True
self._count_success += 1
# 現在のツリーをファイル化する
self._save_current_tree()
# 干渉の有無に関わらずにタイムアウトの確認はする
now_time = time.time()
if now_time - start_time >= self._TIMEOUT_VALUE:
# タイムアウト
break
if result:
# 経路生成に成功のため,経路生成の終了処理
self._fin_planning(start_pos, end_pos)
return result
def _calc_cost(self, pos, near_node):
"""
ノードのコストを計算
パラメータ
pos(numpy.ndarray): 新規ノード位置
near_node(int): 新規ノードとの最短ノード
戻り値
cost(float): コスト
"""
# 最短ノードの情報を保存
node = self._debug_pathes[near_node]
node_pos = node[:self._NODE_NEAR_NODE_IDX]
node_near_node = node[self._NODE_NEAR_NODE_IDX]
node_cost = node[self._NODE_COST_IDX]
# 最短ノードと新規ノードのコスト(距離)を算出
cost = np.linalg.norm(node_pos - pos)
cost += node_cost
return cost
def _get_near_node_list(self, pos, fin_flg=False):
"""
ノードと近傍ノードをリストで取得
パラメータ
pos(numpy.ndarray): ノード位置
fin_flg(bool): 経路生成の終了フラグ
戻り値
near_node_list(list): 近傍ノードリスト
threshold(float): 近傍判定の閾値
"""
near_node_list = []
# ツリー内全ノード位置を取得
all_node_pos = self._debug_pathes[:, :self._NODE_NEAR_NODE_IDX]
# ノードとツリー内全ノードの差分を計算
difference = all_node_pos - pos
# 差分から距離(ユークリッド距離)を計算
distance = np.linalg.norm(difference, axis=1)
# 一定以内の距離
n_node = self._debug_pathes.shape[0]
threshold = self._near_node_radius * np.power(np.log(n_node) / n_node, 1 / self._dim)
# 距離が一定以内のノードだけを保存
near_node_list = [idx for idx, dist in enumerate(distance) if dist <= threshold]
return near_node_list, threshold
def _get_min_cost_node(self, pos, near_node_list, near_node, near_node_cost):
"""
コストが最小となる近傍ノードを取得
パラメータ
pos(numpy.ndarray): ノード位置
near_node_list(list): 近傍ノードリスト
near_node(int): 最短ノード
near_node_cost(float): 最短ノード追加時のコスト
戻り値
min_cost_node(int): コスト最小ノード
min_cost(float): コスト最小値
"""
# 戻り値の初期化
min_cost = near_node_cost
min_cost_node = near_node
if not near_node_list:
# 近傍ノードがないため,処理終了
return min_cost_node, min_cost
for node_idx in near_node_list:
# 近傍ノードに関する情報を保存
node = self._debug_pathes[node_idx]
node_pos = node[:self._NODE_NEAR_NODE_IDX]
node_cost = node[self._NODE_COST_IDX]
# コスト(距離)を計算
distance = np.linalg.norm(node_pos - pos)
# 2点間の干渉チェック
is_interference = self._line_interference(node_pos, pos)
if not is_interference:
# 干渉なし
new_cost = distance + node_cost
if new_cost < min_cost:
# 小さくなるため,最短ノードを修正
min_cost_node = node_idx
min_cost = new_cost
return min_cost_node, min_cost
def _update_near_node(self, pos, near_node_list, cost):
"""
近傍ノード内の親ノードを更新
パラメータ
pos(numpy.ndarray): ノード位置
near_node_list(list): 近傍ノードリスト
cost(float): コスト
"""
if not near_node_list:
# 近傍ノードがないため,処理終了
return
# 新規ノードのインデックス番号を保存
new_node_idx = self._debug_pathes.shape[0]
for node_idx in near_node_list:
# 近傍ノードに関する情報を保存
node = self._debug_pathes[node_idx]
node_pos = node[:self._NODE_NEAR_NODE_IDX]
node_near_node = node[self._NODE_NEAR_NODE_IDX]
node_cost = node[self._NODE_COST_IDX]
# コスト(距離)を計算
distance = np.linalg.norm(node_pos - pos)
# 2点間の干渉チェック
is_interference = self._line_interference(node_pos, pos)
if not is_interference:
# 干渉なし
new_cost = distance + cost
if new_cost < node_cost:
# 小さくなるため,最短ノードを修正
self._debug_pathes[node_idx, self._NODE_NEAR_NODE_IDX] = new_node_idx
self._debug_pathes[node_idx, self._NODE_COST_IDX] = new_cost
def _fin_planning(self, start_pos, end_pos):
"""
経路生成の終了処理
パラメータ
start_pos(list): 経路生成の始点
end_pos(list): 経路生成の終点
"""
# 始点から終点までの経路に関係するノードを選択
revers_path = end_pos
# 終点との最短ノードを取得
near_node = self._get_near_node(end_pos)
# 最短ノードとのコストを計算
near_node_cost = self._calc_cost(end_pos, near_node)
# 近傍ノードを全部取得
near_node_list, threshold = self._get_near_node_list(end_pos, True)
# 近傍ノードからコストが最小となるノードを取得
min_cost_node, min_cost = self._get_min_cost_node(end_pos, near_node_list, near_node, near_node_cost)
near_node = min_cost_node
while True:
# 終点から始点方向へノードを取得
node = self._debug_pathes[near_node, :]
pos = node[:self._NODE_NEAR_NODE_IDX].reshape(1, -1)
# 浮動小数型になっているので,整数型に型変換
near_node = int(node[self._NODE_NEAR_NODE_IDX])
revers_path = np.append(revers_path, pos, axis=0)
if near_node == INITIAL_NODE_NEAR_NODE:
# 始点ノードまで取得できたため,処理終了
break
# 経路が終点からの順番になっているため,始点から終点とする
self._pathes = revers_path[::-1]
# デバッグ用の経路に終点を追加
array_data = np.array([self._debug_pathes.shape[0] - 1, 0.0, threshold])
self._set_random_node(np.append(end_pos, array_data).reshape(1, -1))
self._set_node(np.append(end_pos, array_data).reshape(1, -1))
def _save_current_tree(self):
"""
現在のツリーをファイル化
"""
# 新規ノードが追加できたら,self._count_successはインクリメントされていく
file_name = f"{self._FOLDER_NAME_CURRENT_TREE}/{self._FILE_NAME_CURRENT_TREE}_{self._count_success}.csv"
np.savetxt(file_name, self._debug_pathes)
円形の干渉物との干渉判定
前記事とソースコードは同じため,本記事では割愛する.
前記事 (https://qiita.com/haruhiro1020/items/74ed385c068d4268f4d5) の "interference.py" に記載.
経路生成のアニメーション/グラフ
上記で RRT/RRT-Connect/RRT* の実装をしたが,想定通りに動いているかの確認が必要なため,アニメーション/グラフを作成して確認する.
Pythonによる RRT/RRT-Connect/RRT* のアニメーション実装は下記の通りです.
# RRTで作成した経路のアニメーションを作成する
# ライブラリの読み込み
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as ani
import matplotlib.patches as patches
# 自作モジュールの読み込み
from constant import *
class RRTAnimation:
"""
RRTのアニメーション作成
プロパティ
_min_pos(numpy.ndarray): RRTの最小探索範囲
_max_pos(numpy.ndarray): RRTの最大探索範囲
_figure: 描画枠
_axis: 描画内容
publicメソッド (全てのクラスから参照可能)
plot(): グラフ作成
plot_Animation(): アニメーション作成
protectedメソッド (自クラスまたは子クラスが参照可能)
_plot_2D(): 2D(2次元)グラフ作成
_plot_2DAnimation(): 2D(2次元)アニメーション作成
_reset2D(): 2次元データのリセット
_plot_2Dinterference_obj(): 2次元の干渉物(円形)をプロット
_plot_3D(): 3D(3次元)グラフ作成
_plot_3DAnimation(): 3D(3次元)アニメーション作成
_reset3D(): 3次元データのリセット
_set_3DAxis(): 3次元データのラベルや範囲を設定
_update_3Ddata(): 3次元各データの更新
_plot_3Dinterference_obj(): 3次元の干渉物(球)のプロット
"""
# 定数の定義
_ONE_CUT_NUM = 6 # 1回
_ANIMATION_NAME = "rrt_animation.gif"
_PLOT_NAME = "rrt_plot.gif"
_NODE_NEAR_NODE_IDX = RRT_NEAR_NODE_IDX # ノード内の最短ノード要素
def __init__(self, min_pos, max_pos):
"""
コンストラクタ
"""
self._min_pos = min_pos
self._max_pos = max_pos
def _reset2D(self):
"""
2次元データのリセット
"""
self._figure = plt.Figure()
self._axis = self._figure.add_subplot(111)
# X/Y軸に文字を記載
self._axis.set_xlabel("X")
self._axis.set_ylabel("Y")
# プロットするX/Yの範囲を設定
self._axis.set_xlim(self._min_pos[0], self._max_pos[0])
self._axis.set_ylim(self._min_pos[1], self._max_pos[1])
self._axis.grid()
self._axis.set_aspect("equal")
def _plot_2Dinterference_obj(self, interference_obj):
"""
円形の干渉物のプロット
パラメータ
interference_obj(list): 円形の干渉物
戻り値
interference_images(list): 円形の干渉物
"""
for interference in interference_obj:
# 円形データをプロット
circle = patches.Circle(interference.center, interference.radius, color='gray', alpha=0.5)
self._axis.add_patch(circle)
def _plot_2D_all_node_parent(self, pathes, positions, parent_nodes, line_color="red"):
"""
全ノードを親ノード(最短ノード)と一緒にプロット(2次元データ)
パラメータ
pathes(numpy.ndarray): 始点から終点までの経路
positions(numpy.ndarray): 全ノード位置
parent_nodes(numpy.ndarray): 全ノードの親ノード
line_color(str): ノードと親ノードの直線の色
戻り値
path_images(list): 全ノードをプロットしたリストデータ
"""
path_images = []
# 引数の確認
if positions.shape[0] != parent_nodes.shape[0]:
# データ数不一致で異常
return
# ノードを全部プロット
image = self._axis.scatter(positions[ :, 0], positions[ :, 1], color="gray", marker="*")
path_images.extend([image])
# 始点をプロット
image = self._axis.scatter(pathes[ 0, 0], pathes[ 0, 1], color="cyan", marker="*")
path_images.extend([image])
# 終点をプロット
image = self._axis.scatter(pathes[-1, 0], pathes[-1, 1], color="lime", marker="*")
path_images.extend([image])
for i in reversed(range(1, positions.shape[0])):
# 追加の遅いノードから順番にプロットしていく
now_position = positions[i]
now_node = i
near_node_idx = int(parent_nodes[i])
while True: # 始点をプロットするまでループ
parent_position = positions[near_node_idx]
plot_pos = np.append(now_position.reshape(1, -1), parent_position.reshape(1, -1), axis=0)
# 親ノードとの線をプロット
image = self._axis.plot(plot_pos[:, 0], plot_pos[:, 1], color=line_color)
path_images.extend(image)
# ノードおよび親ノードの更新
now_position = parent_position
near_node_idx = int(parent_nodes[near_node_idx])
if near_node_idx == INITIAL_NODE_NEAR_NODE:
# 始点には,親ノードが存在しないから,while処理を抜ける
break
# 最終的なパスをプロット
image = self._axis.plot(pathes[:, 0], pathes[:, 1], color="green", alpha=0.7)
path_images.extend(image)
return path_images
def plot(self, pathes, debug_pathes, interference_obj, dimention):
"""
グラフ作成
パラメータ
pathes(numpy.ndarray): 経路
debug_pathes(numpy.ndarray): デバッグ用経路
interference_obj(list): 円形の干渉物
dimention(int): 次元数
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# 引数の確認
if pathes.size == 0 or debug_pathes.size == 0:
return plot_result
# デバッグ用経路から位置・親ノードを取得
debug_pathes_position = debug_pathes[:, :self._NODE_NEAR_NODE_IDX]
debug_pathes_near_node = debug_pathes[:, self._NODE_NEAR_NODE_IDX]
if dimention == DIMENTION_2D: # 2次元データ
plot_result = self._plot_2D(pathes, debug_pathes_position, debug_pathes_near_node, interference_obj)
elif dimention == DIMENTION_3D: # 3次元データ
plot_result = self._plot_3D(pathes, debug_pathes_position, debug_pathes_near_node, interference_obj)
return plot_result
def _plot_2D(self, pathes, debug_pathes_position, debug_pathes_near_node, interference_obj):
"""
2D(2次元)グラフ作成
パラメータ
pathes(numpy.ndarray): 経路
debug_pathes_position(numpy.ndarray): デバッグ用経路のノード位置
debug_pathes_near_node(numpy.ndarray): デバッグ用経路の親ノード
interference_obj(list): 円形の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset2D()
# 干渉物をプロット
self._plot_2Dinterference_obj(interference_obj)
imgs = []
# 全ノードを親ノード(最短ノード)と一緒にプロット
path_images = self._plot_2D_all_node_parent(pathes, debug_pathes_position, debug_pathes_near_node)
if path_images:
for _ in range(self._ONE_CUT_NUM):
imgs.append(path_images)
# アニメーション
animation = ani.ArtistAnimation(self._figure, imgs)
animation.save(self._PLOT_NAME, writer='imagemagick')
plt.show()
plot_result = True
return plot_result
def plot_Animation(self, pathes, debug_pathes, debug_random_pathes, interference_obj, dimention):
"""
アニメーション作成
パラメータ
pathes(numpy.ndarray): 経路
debug_pathes(numpy.ndarray): デバッグ用経路
debug_random_pathes(numpy.ndarray): デバッグ用ランダム経路
interference_obj(list): 円形の干渉物
dimention(int): 次元数
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# 引数の確認
if pathes.size == 0 or debug_pathes.size == 0 or debug_random_pathes.size == 0:
return plot_result
# デバッグ用経路とデバッグ用ランダム経路の行数が一致していることを確認
if debug_pathes.shape[0] != debug_random_pathes.shape[0]:
# 異常なデータ
return plot_result
# デバッグ用経路から位置・親ノードを取得
debug_pathes_position = debug_pathes[:, :self._NODE_NEAR_NODE_IDX]
debug_pathes_near_node = debug_pathes[:, self._NODE_NEAR_NODE_IDX]
# デバッグ用ランダム経路から位置・親ノードを取得
debug_random_pathes_position = debug_random_pathes[:, :self._NODE_NEAR_NODE_IDX]
debug_random_pathes_near_node = debug_random_pathes[:, self._NODE_NEAR_NODE_IDX]
if dimention == DIMENTION_2D: # 2次元データ
plot_result = self._plot_2DAnimation(pathes, debug_pathes_position, debug_pathes_near_node, debug_random_pathes_position, interference_obj)
elif dimention == DIMENTION_3D: # 3次元データ
plot_result = self._plot_3DAnimation(pathes, debug_pathes_position, debug_pathes_near_node, debug_random_pathes_position, interference_obj)
return plot_result
def _plot_2DAnimation(self, pathes, debug_pathes_pos, debug_pathes_near_node, debug_random_pathes_pos, interference_obj):
"""
2D(2次元)アニメーション作成
パラメータ
pathes(numpy.ndarray): 経路
debug_pathes_pos(numpy.ndarray): デバッグ用経路の位置
debug_pathes_near_node(numpy.ndarray): デバッグ用経路の親ノード
debug_random_pathes_pos(numpy.ndarray): デバッグ用ランダム経路の位置
interference_obj(list): 円形の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset2D()
# 円形の干渉物をプロット
self._plot_2Dinterference_obj(interference_obj)
imgs = []
# アニメーション
for i in range(debug_pathes_pos.shape[0]):
for j in range(self._ONE_CUT_NUM * 2):
# デバッグ用経路の点数分ループ
path_images = []
# ランダムな経路をプロット
image = self._axis.plot(debug_random_pathes_pos[i, 0], debug_random_pathes_pos[i, 1], color="red", marker="*")
path_images.extend(image)
# ノードをプロット
image = self._axis.scatter(debug_pathes_pos[:i, 0], debug_pathes_pos[:i, 1], color="black", marker="*")
path_images.extend([image])
# 始点をプロット
image = self._axis.scatter(debug_pathes_pos[ 0, 0], debug_pathes_pos[ 0, 1], color="cyan", marker="*", s=24)
path_images.extend([image])
# 終点をプロット
image = self._axis.scatter(debug_pathes_pos[-1, 0], debug_pathes_pos[-1, 1], color="lime", marker="*", s=24)
path_images.extend([image])
# 現ノードをプロット
image = self._axis.scatter(debug_pathes_pos[ i, 0], debug_pathes_pos[ i, 1], color="blue", s=24)
path_images.extend([image])
# 最短ノードもプロット
if i != 0:
# 始点には最短ノードが存在しないから,始点以外でプロットする
near_node = int(debug_pathes_near_node[i])
plot_pos = np.append(debug_pathes_pos[i].reshape(1, -1), debug_pathes_pos[near_node].reshape(1, -1), axis=0)
image = self._axis.plot(plot_pos[:, 0], plot_pos[:, 1], color="red")
path_images.extend(image)
image = self._axis.scatter(plot_pos[1, 0], plot_pos[1, 1], color="green", marker="*", s=24)
path_images.extend([image])
imgs.append(path_images)
# 最終的なパスをプロット
for _ in range(self._ONE_CUT_NUM * 4):
path_images = []
image = self._axis.plot(pathes[:, 0], pathes[:, 1], color="green")
path_images.extend(image)
image = self._axis.scatter(debug_pathes_pos[:, 0], debug_pathes_pos[:, 1], color="gray")
path_images.extend([image])
imgs.append(path_images)
# アニメーション
animation = ani.ArtistAnimation(self._figure, imgs)
animation.save(self._ANIMATION_NAME, writer='imagemagick')
plt.show()
plot_result = True
return plot_result
def _reset3D(self):
"""
3次元データのリセット
"""
self._figure = plt.figure()
self._axis = self._figure.add_subplot(111, projection="3d")
# 0 ~ 2piまでの範囲とする
theta_1_0 = np.linspace(0, np.pi * 2, 100)
theta_2_0 = np.linspace(0, np.pi * 2, 100)
theta_1, theta_2 = np.meshgrid(theta_1_0, theta_2_0)
# x, y, zの曲座標表示 (中心点が原点である半径1の球)
self._x = np.cos(theta_2) * np.sin(theta_1)
self._y = np.sin(theta_2) * np.sin(theta_1)
self._z = np.cos(theta_1)
def _set_3DAxis(self):
"""
3次元データのラベルや範囲を設定
"""
# X/Y/Z軸に文字を記載
self._axis.set_xlabel("X")
self._axis.set_ylabel("Y")
self._axis.set_zlabel("Z")
# プロットするX/Y/Zの範囲を設定
self._axis.set_xlim(self._min_pos[0], self._max_pos[0])
self._axis.set_ylim(self._min_pos[1], self._max_pos[1])
self._axis.set_zlim(self._min_pos[2], self._max_pos[2])
self._axis.grid()
self._axis.set_aspect("equal")
def _update_3Ddata(self, i, pathes, debug_pathes_pos, debug_pathes_near_node, debug_random_pathes, interference_obj):
"""
3D(3次元)各データの更新
パラメータ
i(int): フレーム番号
pathes(numpy.ndarray): 経路
debug_pathes_position(numpy.ndarray): デバッグ用経路のノード位置
debug_pathes_near_node(numpy.ndarray): デバッグ用経路の親ノード
debug_random_pathes(numpy.ndarray): デバッグ用ランダム経路
interference_obj(list): 干渉物
"""
# 以前のプロットをクリアする
self._axis.clear()
self._set_3DAxis()
# 干渉物のプロット
self._plot_3Dinterference_obj(interference_obj)
if i < debug_pathes_pos.shape[0]:
# 各ノードをプロットする
# ランダムな経路をプロット
self._axis.plot(debug_random_pathes[i, 0], debug_random_pathes[i, 1], debug_random_pathes[i, 2], color="red", marker="*")
# ノードをプロット
self._axis.scatter(debug_pathes_pos[:i, 0], debug_pathes_pos[:i, 1], debug_pathes_pos[:i, 2], color="black", marker="*")
# 始点をプロット
self._axis.scatter(debug_pathes_pos[ 0, 0], debug_pathes_pos[ 0, 1], debug_pathes_pos[ 0, 2], color="cyan", marker="*", s=24)
# 終点をプロット
self._axis.scatter(debug_pathes_pos[-1, 0], debug_pathes_pos[-1, 1], debug_pathes_pos[-1, 2], color="lime", marker="*", s=24)
# 現ノードをプロット
self._axis.scatter(debug_pathes_pos[ i, 0], debug_pathes_pos[ i, 1], debug_pathes_pos[ i, 2], color="blue", s=24)
# 最短ノードもプロット
if i != 0:
# 始点には最短ノードが存在しないから,始点以外でプロットする
near_node = int(debug_pathes_near_node[i])
plot_pos = np.append(debug_pathes_pos[i].reshape(1, -1), debug_pathes_pos[near_node].reshape(1, -1), axis=0)
self._axis.plot(plot_pos[:, 0], plot_pos[:, 1], plot_pos[:, 2], color="red")
self._axis.scatter(plot_pos[1, 0], plot_pos[1, 1], plot_pos[1, 2], color="green", marker="*", s=24)
else:
# 生成した経路をプロットする
self._axis.plot(pathes[:, 0], pathes[:, 1], pathes[:, 2], color="green")
self._axis.scatter(debug_pathes_pos[:, 0], debug_pathes_pos[:, 1], debug_pathes_pos[:, 2], color="gray")
def _plot_3Dinterference_obj(self, interference_obj):
"""
球の干渉物のプロット
パラメータ
interference_obj(list): 球の干渉物
戻り値
interference_images(list): 干渉物データ
"""
for interference in interference_obj:
# 球データをプロット
center = interference.center
self._axis.plot_wireframe(self._x * interference.radius + center[0], self._y * interference.radius + center[1], self._z * interference.radius + center[2], color="gray", alpha=0.1)
def _plot_3D_all_node_parent(self, pathes, positions, parent_nodes, line_color="red"):
"""
全ノードを親ノード(最短ノード)と一緒にプロット(3次元データ)
パラメータ
pathes(numpy.ndarray): 始点から終点までの経路
positions(numpy.ndarray): 全ノード位置
parent_nodes(numpy.ndarray): 全ノードの親ノード
戻り値
path_images(list): 全ノードをプロットしたリストデータ
"""
path_images = []
# 引数の確認
if positions.shape[0] != parent_nodes.shape[0]:
# データ数不一致で異常
return
# ノードを全部プロット
image = self._axis.scatter(positions[ :, 0], positions[ :, 1], positions[ :, 2], color="gray", marker="*")
path_images.extend([image])
# 始点をプロット
image = self._axis.scatter(pathes[ 0, 0], pathes[ 0, 1], pathes[ 0, 2], color="cyan", marker="*")
path_images.extend([image])
# 終点をプロット
image = self._axis.scatter(pathes[-1, 0], pathes[-1, 1], pathes[-1, 2], color="lime", marker="*")
path_images.extend([image])
for i in reversed(range(1, positions.shape[0])):
# 追加の遅いノードから順番にプロットしていく
now_position = positions[i]
now_node = i
near_node_idx = int(parent_nodes[i])
while True: # 始点をプロットするまでループ
parent_position = positions[near_node_idx]
plot_pos = np.append(now_position.reshape(1, -1), parent_position.reshape(1, -1), axis=0)
# 親ノードとの線をプロット
image = self._axis.plot(plot_pos[:, 0], plot_pos[:, 1], plot_pos[:, 2], color=line_color)
path_images.extend(image)
# ノードおよび親ノードの更新
now_position = parent_position
near_node_idx = int(parent_nodes[near_node_idx])
if near_node_idx == INITIAL_NODE_NEAR_NODE:
# 始点には,親ノードが存在しないから,while処理を抜ける
break
# 最終的なパスをプロット
image = self._axis.plot(pathes[:, 0], pathes[:, 1], pathes[:, 2], color="green", alpha=0.7)
path_images.extend(image)
return path_images
def _plot_3D(self, pathes, debug_pathes_position, debug_pathes_near_node, interference_obj):
"""
3D(3次元)グラフ作成
パラメータ
pathes(numpy.ndarray): 経路
debug_pathes_position(numpy.ndarray): デバッグ用経路のノード位置
debug_pathes_near_node(numpy.ndarray): デバッグ用経路の親ノード
interference_obj(list): 円形の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset3D()
# 干渉物をプロット
self._plot_3Dinterference_obj(interference_obj)
imgs = []
# 全ノードを親ノード(最短ノード)と一緒にプロット
path_images = self._plot_3D_all_node_parent(pathes, debug_pathes_position, debug_pathes_near_node)
if path_images:
for _ in range(self._ONE_CUT_NUM):
imgs.append(path_images)
# アニメーション
animation = ani.ArtistAnimation(self._figure, imgs)
animation.save(self._PLOT_NAME, writer='imagemagick')
plt.show()
plot_result = True
return plot_result
def _plot_3DAnimation(self, pathes, debug_pathes_pos, debug_pathes_near_node, debug_random_pathes_pos, interference_obj):
"""
3D(3次元)アニメーション作成
パラメータ
pathes(numpy.ndarray): 経路
debug_pathes_pos(numpy.ndarray): デバッグ用経路の位置
debug_pathes_near_node(numpy.ndarray): デバッグ用経路の親ノード
debug_random_pathes_pos(numpy.ndarray): デバッグ用ランダム経路の位置
interference_obj(list): 球の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset3D()
# アニメーションのフレーム数
n_frame = debug_pathes_pos.shape[0] + self._ONE_CUT_NUM * 4
animation = ani.FuncAnimation(self._figure, self._update_3Ddata, fargs=(pathes, debug_pathes_pos, debug_pathes_near_node, debug_random_pathes_pos, interference_obj), interval=500, frames=n_frame)
# アニメーション
animation.save(self._ANIMATION_NAME, writer="imagemagick")
plt.show()
plot_result = True
return plot_result
class RRTConnectAnimation(RRTAnimation):
"""
RRT-Connectのアニメーション作成
プロパティ
_figure: 描画枠
_axis: 描画内容
_start_tree_idx(int): 始点ツリーのノード番号
_end_tree_idx(int): 終点ツリーのノード番号
publicメソッド (全てのクラスから参照可能)
plot(): グラフ作成
plot_Animation(): アニメーション作成
protectedメソッド (自クラスまたは子クラスが参照可能)
_plot_2D_data(): 2次元データのプロット
_plot_2D(): 2D(2次元)グラフ作成
_plot_2DAnimation(): 2D(2次元)アニメーション作成
_update_3Ddata(): 3D(3次元)各データの更新
_plot_3DAnimation(): 3D(3次元)アニメーション作成
_plot_3D_data(): 3D(3次元)各データのプロット
_reset3D(): 3次元データのリセット
"""
# 定数の定義
_ONE_CUT_NUM = 6 # 1回
_ANIMATION_NAME = "rrt_connect_animation.gif" # アニメーション保存ファイル名
_PLOT_NAME = "rrt_connect_plot.gif" # グラフ保存ファイル名
def __init__(self, min_pos, max_pos):
"""
コンストラクタ
"""
# 親クラスの初期化処理
super().__init__(min_pos, max_pos)
def plot(self, pathes, start_tree, end_tree, interference_obj, dimention):
"""
グラフ作成
パラメータ
pathes(numpy.ndarray): 経路
start_tree(numpy.ndarray): 始点ツリー
end_tree(numpy.ndarray): 終点ツリー
interference_obj(list): 円形の干渉物
dimention(int): 次元数
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# 引数の確認
if pathes.size == 0 or start_tree.size == 0 or end_tree.size == 0:
return plot_result
# 始点ツリーを位置と親ノードに分割
start_tree_pos = start_tree[:, :RRT_CONNECT_NEAR_NODE_IDX]
start_tree_near_node = start_tree[:, RRT_CONNECT_NEAR_NODE_IDX]
# 終点ツリーを位置と親ノードに分割
end_tree_pos = end_tree[:, :RRT_CONNECT_NEAR_NODE_IDX]
end_tree_near_node = end_tree[:, RRT_CONNECT_NEAR_NODE_IDX]
if dimention == DIMENTION_2D:
plot_result = self._plot_2D(pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, interference_obj)
elif dimention == DIMENTION_3D:
plot_result = self._plot_3D(pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, interference_obj)
return plot_result
def _plot_2D(self, pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, interference_obj):
"""
2D(2次元)グラフ作成
パラメータ
pathes(numpy.ndarray): 経路
start_tree_pos(numpy.ndarray): 始点ツリーのノード位置
start_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
end_tree_pos(numpy.ndarray): 始点ツリーのノード位置
end_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
interference_obj(list): 円形の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset2D()
# 円形の干渉物をプロット
self._plot_2Dinterference_obj(interference_obj)
imgs = []
# 始点ツリー内の全ノードを親ノード(最短ノード)と一緒にプロット
path_images_start_tree = self._plot_2D_all_node_parent(pathes, start_tree_pos, start_tree_near_node, "red")
# 終点ツリー内の全ノードを親ノードと一緒にプロット
path_images_end_tree = self._plot_2D_all_node_parent(pathes, end_tree_pos, end_tree_near_node, "blue")
if path_images_start_tree and path_images_end_tree:
path_images_start_end_tree = []
path_images_start_end_tree.extend(path_images_start_tree)
path_images_start_end_tree.extend(path_images_end_tree)
for _ in range(self._ONE_CUT_NUM):
imgs.append(path_images_start_end_tree)
# アニメーション
animation = ani.ArtistAnimation(self._figure, imgs)
animation.save(self._PLOT_NAME, writer='imagemagick')
plt.show()
plot_result = True
return plot_result
def _plot_2DAnimation(self, pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states, interference_obj):
"""
2D(2次元)アニメーション作成
パラメータ
pathes(numpy.ndarray): 経路
start_tree_pos(numpy.ndarray): 始点ツリーのノード位置
start_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
end_tree_pos(numpy.ndarray): 始点ツリーのノード位置
end_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
debug_states(list): デバッグ用の状態
interference_obj(list): 円形の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset2D()
# 円形の干渉物をプロット
self._plot_2Dinterference_obj(interference_obj)
self._plot_2D_data(pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states)
plot_result = True
return plot_result
def _plot_2D_data(self, pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states):
"""
2D(2次元)データのプロット
パラメータ
pathes(numpy.ndarray): 経路
start_tree_pos(numpy.ndarray): 始点ツリーのノード位置
start_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
end_tree_pos(numpy.ndarray): 始点ツリーのノード位置
end_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
debug_states(list): デバッグ用の状態
"""
# 各ツリーの要素番号を定義
start_tree_idx = 0
end_tree_idx = 0
# ノードを追加したツリーを保存
now_tree_pos = start_tree_pos
now_tree_near_node = start_tree_near_node
imgs = []
# アニメーション
for idx, state in enumerate(debug_states):
# 状態の数分ループ
path_images = []
if state == STATE_START_TREE_RANDOM or state == STATE_START_TREE_END_TREE:
# 始点ツリーにランダム点を追加状態または始点ツリーから終点ツリーへノードを伸ばす状態
start_tree_idx += 1
# 追加した点の位置を取得
now_pos = start_tree_pos[start_tree_idx]
# 追加した点の最短ノードを取得
near_node = int(start_tree_near_node[start_tree_idx])
# 最短ノードの位置を取得
near_pos = start_tree_pos[near_node]
else:
# 終点ツリーにランダム点を追加状態または終点ツリーから始点ツリーへノードを伸ばす状態
end_tree_idx += 1
# 追加した点の位置を取得
now_pos = end_tree_pos[end_tree_idx]
# 追加した点の最短ノードを取得
near_node = int(end_tree_near_node[end_tree_idx])
# 最短ノードの位置を取得
near_pos = end_tree_pos[near_node]
# 生成できている始点ツリーをプロット
image = self._axis.scatter(start_tree_pos[:start_tree_idx + 1, 0], start_tree_pos[:start_tree_idx + 1, 1], color="red", marker="*")
path_images.extend([image])
# 生成できている終点ツリーをプロット
image = self._axis.scatter(end_tree_pos[:end_tree_idx + 1, 0], end_tree_pos[:end_tree_idx + 1, 1], color="orange", marker="*")
path_images.extend([image])
# 始点をプロット
image = self._axis.scatter(start_tree_pos[0, 0], start_tree_pos[0, 1], color="cyan", marker="*", s=24)
path_images.extend([image])
# 終点をプロット
image = self._axis.scatter(end_tree_pos[0, 0], end_tree_pos[0, 1], color="lime", marker="*", s=24)
path_images.extend([image])
# 現ノードをプロット
image = self._axis.scatter(now_pos[0], now_pos[1], color="blue", s=24)
path_images.extend([image])
# 最短ノードもプロット
plot_pos = np.append(now_pos.reshape(1, -1), near_pos.reshape(1, -1), axis=0)
image = self._axis.plot(plot_pos[:, 0], plot_pos[:, 1], color="red")
path_images.extend(image)
image = self._axis.scatter(plot_pos[1, 0], plot_pos[1, 1], color="green", marker="*", s=24)
path_images.extend([image])
# 相手ツリーのランダムノードをプロット
if state == STATE_START_TREE_END_TREE:
# 終点ツリーのランダムノードをプロット
image = self._axis.scatter(end_tree_pos[end_tree_idx, 0], end_tree_pos[end_tree_idx, 1], color="green")
path_images.extend([image])
elif state == STATE_END_TREE_START_TREE:
image = self._axis.scatter(start_tree_pos[start_tree_idx, 0], start_tree_pos[start_tree_idx, 1], color="green")
path_images.extend([image])
imgs.append(path_images)
for _ in range(self._ONE_CUT_NUM):
path_images = []
# 最終的なパスをプロット
image = self._axis.plot(pathes[:, 0], pathes[:, 1], color="green")
path_images.extend(image)
# 始点ツリーをプロット
image = self._axis.scatter(start_tree_pos[:, 0], start_tree_pos[:, 1], color="gray")
path_images.extend([image])
# 終点ツリーをプロット
image = self._axis.scatter(end_tree_pos[:, 0], end_tree_pos[:, 1], color="gray")
path_images.extend([image])
imgs.append(path_images)
# アニメーション
animation = ani.ArtistAnimation(self._figure, imgs, interval=500)
animation.save(self._ANIMATION_NAME, writer='imagemagick')
plt.show()
def _update_3Ddata(self, i, pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states, interference_obj):
"""
3D(3次元)各データの更新
パラメータ
i(int): フレーム番号
pathes(numpy.ndarray): 経路
start_tree_pos(numpy.ndarray): 始点ツリーのノード位置
start_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
end_tree_pos(numpy.ndarray): 始点ツリーのノード位置
end_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
debug_states(list): デバッグ用の状態
interference_obj(list): 干渉物
"""
# 以前のプロットをクリアする
self._axis.clear()
self._set_3DAxis()
# 干渉物のプロット
self._plot_3Dinterference_obj(interference_obj)
if i == 0:
# フレーム数が初期値の場合は,ツリーのインデックス番号を初期化する
self._start_tree_idx = 0
self._end_tree_idx = 0
self._plot_3D_data(i, pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states)
def _plot_3D_data(self, i, pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states):
"""
3D(3次元)各データのプロット
パラメータ
i(int): フレーム番号
pathes(numpy.ndarray): 経路
start_tree_pos(numpy.ndarray): 始点ツリーのノード位置
start_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
end_tree_pos(numpy.ndarray): 始点ツリーのノード位置
end_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
debug_states(list): デバッグ用の状態
"""
if i < len(debug_states):
# 状態に応じた処理を実施する
state = debug_states[i]
if state == STATE_START_TREE_RANDOM or state == STATE_START_TREE_END_TREE:
# 始点ツリーにランダム点を追加状態または始点ツリーから終点ツリーへノードを伸ばす状態
self._start_tree_idx += 1
# 追加した点の位置を取得
now_pos = start_tree_pos[self._start_tree_idx]
# 追加した点の最短ノードを取得
near_node = int(start_tree_near_node[self._start_tree_idx])
# 最短ノードの位置を取得
near_pos = start_tree_pos[near_node]
else:
# 終点ツリーにランダム点を追加状態または終点ツリーから始点ツリーへノードを伸ばす状態
self._end_tree_idx += 1
# 追加した点の位置を取得
now_pos = end_tree_pos[self._end_tree_idx]
# 追加した点の最短ノードを取得
near_node = int(end_tree_near_node[self._end_tree_idx])
# 最短ノードの位置を取得
near_pos = end_tree_pos[near_node]
# 生成できている始点ツリーをプロット
self._axis.scatter(start_tree_pos[:self._start_tree_idx + 1, 0], start_tree_pos[:self._start_tree_idx + 1, 1], start_tree_pos[:self._start_tree_idx + 1, 2],color="red", marker="*")
# 生成できている終点ツリーをプロット
self._axis.scatter(end_tree_pos[:self._end_tree_idx + 1, 0], end_tree_pos[:self._end_tree_idx + 1, 1], end_tree_pos[:self._end_tree_idx + 1, 2], color="orange", marker="*")
# 始点をプロット
self._axis.scatter(start_tree_pos[0, 0], start_tree_pos[0, 1], start_tree_pos[0, 2], color="cyan", marker="*", s=24)
# 終点をプロット
self._axis.scatter(end_tree_pos[0, 0], end_tree_pos[0, 1], end_tree_pos[0, 2], color="lime", marker="*", s=24)
# 現ノードをプロット
self._axis.scatter(now_pos[0], now_pos[1], now_pos[2], color="blue", s=24)
# 最短ノードもプロット
plot_pos = np.append(now_pos.reshape(1, -1), near_pos.reshape(1, -1), axis=0)
self._axis.plot(plot_pos[:, 0], plot_pos[:, 1], plot_pos[:, 2], color="red")
self._axis.scatter(plot_pos[1, 0], plot_pos[1, 1], plot_pos[1, 2], color="green", marker="*", s=24)
# 相手ツリーのランダムノードをプロット
if state == STATE_START_TREE_END_TREE:
# 終点ツリーのランダムノードをプロット
self._axis.scatter(end_tree_pos[self._end_tree_idx, 0], end_tree_pos[self._end_tree_idx, 1], end_tree_pos[self._end_tree_idx, 2], color="green")
elif state == STATE_END_TREE_START_TREE:
self._axis.scatter(start_tree_pos[self._start_tree_idx, 0], start_tree_pos[self._start_tree_idx, 1], start_tree_pos[self._start_tree_idx, 2], color="green")
else:
# 生成した経路をプロットする
self._axis.plot(pathes[:, 0], pathes[:, 1], pathes[:, 2], color="green")
self._axis.scatter(start_tree_pos[:, 0], start_tree_pos[:, 1], start_tree_pos[:, 2], color="gray")
self._axis.scatter(end_tree_pos[:, 0], end_tree_pos[:, 1], end_tree_pos[:, 2], color="gray")
def _reset3D(self):
"""
3次元データのリセット
"""
# 親クラスのリセット処理
super()._reset3D()
# ツリーの要素番号をリセット
self._start_tree_idx = 0
self._end_tree_idx = 0
def _plot_3D(self, pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, interference_obj):
"""
3D(3次元)グラフ作成
パラメータ
pathes(numpy.ndarray): 経路
start_tree_pos(numpy.ndarray): 始点ツリーのノード位置
start_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
end_tree_pos(numpy.ndarray): 始点ツリーのノード位置
end_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
interference_obj(list): 円形の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset3D()
# 円形の干渉物をプロット
self._plot_3Dinterference_obj(interference_obj)
imgs = []
# 始点ツリー内の全ノードを親ノード(最短ノード)と一緒にプロット (始点ツリーを赤色とする)
path_images_start_tree = self._plot_3D_all_node_parent(pathes, start_tree_pos, start_tree_near_node, "red")
# 終点ツリー内の全ノードを親ノードと一緒にプロット (終点ツリーを青色とする)
path_images_end_tree = self._plot_3D_all_node_parent(pathes, end_tree_pos, end_tree_near_node, "blue")
if path_images_start_tree and path_images_end_tree:
path_images_start_end_tree = []
path_images_start_end_tree.extend(path_images_start_tree)
path_images_start_end_tree.extend(path_images_end_tree)
for _ in range(self._ONE_CUT_NUM):
imgs.append(path_images_start_end_tree)
# アニメーション
animation = ani.ArtistAnimation(self._figure, imgs)
animation.save(self._PLOT_NAME, writer='imagemagick')
plt.show()
plot_result = True
return plot_result
def _plot_3DAnimation(self, pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states, interference_obj):
"""
3D(3次元)アニメーション作成
パラメータ
pathes(numpy.ndarray): 経路
start_tree_pos(numpy.ndarray): 始点ツリーのノード位置
start_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
end_tree_pos(numpy.ndarray): 始点ツリーのノード位置
end_tree_near_node(numpy.ndarray): 始点ツリーの親ノード
debug_states(list): デバッグ用の状態
interference_obj(list): 球の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset3D()
# アニメーションのフレーム数
n_frame = len(debug_states) + self._ONE_CUT_NUM
animation = ani.FuncAnimation(self._figure, self._update_3Ddata, fargs=(pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states, interference_obj), interval=500, frames=n_frame)
# アニメーション
animation.save(self._ANIMATION_NAME, writer="imagemagick")
plt.show()
plot_result = True
return plot_result
def plot_Animation(self, pathes, start_tree, end_tree, debug_states, interference_obj, dimention):
"""
アニメーション作成
パラメータ
pathes(numpy.ndarray): 経路
start_tree(numpy.ndarray): 始点ツリー
end_tree(numpy.ndarray): 終点ツリー
debug_states(list): デバッグ用の状態
interference_obj(list): 干渉物
dimention(int): 次元数
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# 引数の確認
if pathes.size == 0 or start_tree.size == 0 or end_tree.size == 0 or len(debug_states) == 0:
return plot_result
# 始点ツリーを位置と親ノードに分割
start_tree_pos = start_tree[:, :RRT_CONNECT_NEAR_NODE_IDX]
start_tree_near_node = start_tree[:, RRT_CONNECT_NEAR_NODE_IDX]
# 終点ツリーを位置と親ノードに分割
end_tree_pos = end_tree[:, :RRT_CONNECT_NEAR_NODE_IDX]
end_tree_near_node = end_tree[:, RRT_CONNECT_NEAR_NODE_IDX]
if dimention == DIMENTION_2D: # 2次元データ
plot_result = self._plot_2DAnimation(pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states, interference_obj)
elif dimention == DIMENTION_3D: # 3次元データ
plot_result = self._plot_3DAnimation(pathes, start_tree_pos, start_tree_near_node, end_tree_pos, end_tree_near_node, debug_states, interference_obj)
return plot_result
class RRTStarAnimation(RRTAnimation):
"""
RRT*のアニメーション作成
プロパティ
_min_pos(numpy.ndarray): RRT*の最小探索範囲
_max_pos(numpy.ndarray): RRT*の最大探索範囲
publicメソッド (全てのクラスから参照可能)
plot_2DAnimation(): 2D(2次元)アニメーション作成
plot_3DAnimation(): 3D(3次元)アニメーション作成
protectedメソッド (自クラスまたは子クラスが参照可能)
_reset2D(): 2次元データのリセット
_reset3D(): 3次元データのリセット
_update_3Ddata(): 3次元各データの更新
"""
# 定数の定義
_ONE_CUT_NUM = 6 # 1回
_ANIMATION_NAME = "rrt_star_animation.gif" # アニメーション保存ファイル名
_PLOT_NAME = "rrt_star_plot.gif" # グラフ保存ファイル名
def __init__(self, min_pos, max_pos):
"""
コンストラクタ
"""
# 親クラスの初期化処理
super().__init__(min_pos, max_pos)
def _plot_2D(self, pathes, debug_pathes_pos, debug_pathes_near_node, interference_obj):
"""
2D(2次元)グラフ作成
パラメータ
pathes(numpy.ndarray): 経路
debug_pathes_pos(numpy.ndarray): デバッグ用経路のノード位置
debug_pathes_near_node(numpy.ndarray): デバッグ用経路の親ノード
interference_obj(list): 円形の干渉物
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# データをリセットする
self._reset2D()
# 円形の干渉物をプロット
self._plot_2Dinterference_obj(interference_obj)
imgs = []
# 全ノードを親ノード(最短ノード)と一緒にプロット
path_images = self._plot_2D_all_node_parent(pathes, debug_pathes_pos, debug_pathes_near_node)
if path_images:
for _ in range(self._ONE_CUT_NUM):
imgs.append(path_images)
# アニメーション
animation = ani.ArtistAnimation(self._figure, imgs)
animation.save(self._PLOT_NAME, writer='imagemagick')
plt.show()
plot_result = True
return plot_result
def plot(self, pathes, folder_name, file_name, n_file, extension, interference_obj, dimention):
"""
グラフ作成
パラメータ
pathes(numpy.ndarray): 経路
folder_name(str): フォルダー名
file_name(str): ファイル名
n_file(int): ファイル数
extension(str): ファイルの拡張子
interference_obj(list): 円形の干渉物
dimention(int): 次元数
戻り値
plot_result(bool): True / False = 成功 / 失敗
"""
plot_result = False
# 引数の確認
if pathes.size == 0 or not folder_name or not file_name or n_file <= 0 or not extension:
# 引数が異常
return plot_result
# プロットするデータが保存されているファイル名
f_name = f"{folder_name}/{file_name}_{n_file}.{extension}"
try:
file_data = np.loadtxt(f_name)
except Exception as e: # ファイル読み込みで例外エラー発生
print(f"Error is {e}")
return plot_result
# ファイルから,位置・最短ノード・コスト・近傍判定の半径に分割
debug_pathes_pos = file_data[:, :RRT_STAR_NEAR_NODE_IDX]
debug_pathes_near_node = file_data[:, RRT_STAR_NEAR_NODE_IDX]
debug_pathes_cost = file_data[:, RRT_STAR_COST_IDX]
debug_pathes_radius = file_data[:, RRT_STAR_RADIUS_IDX]
if dimention == DIMENTION_2D:
plot_result = self._plot_2D(pathes, debug_pathes_pos, debug_pathes_near_node, interference_obj)
# 3次元は未作成のため,処理をしない
return plot_result
性能評価 (RRT/RRT-Connect/RRT*)
RRT/RRT-Connect/RRT* による性能評価を実施する.
性能評価を実施するために,干渉物の位置と大きさを一定として,下記内容を比較することによって,性能を評価していく.各アルゴリズムを30回実施して,性能を評価する.
・始点から終点までの経路生成の処理時間 [sec]
・生成した経路の経由点の数 (始点と終点を含む)
RRT/RRT-Connectでは始点から終点までの経路が作成されたら経路生成を終了するが,RRT* は始点から終点までの経路が作成されても必ず試行回数は500回とした.
性能評価する時のメイン処理は下記の通りである.
# ライブラリの読み込み
import numpy as np
import matplotlib.pyplot as plt
import time
# 自作モジュールの読み込み
from rrt import RRT, RRTConnect, RRTStar # 経路生成アルゴリズム
from rrt_animation import RRTAnimation, RRTConnectAnimation, RRTStarAnimation # 経路生成のアニメーション
from interference import Circle, Ball # 干渉物
from constant import * # 定数
START_POS = 0 # 始点位置
END_POS = 2 # 終点位置
def rrt_planning(dimention, plot_mode, start_pos, end_pos, interference_obj):
"""
RRTによる経路生成
パラメータ
dimention(int): 次元数
plot_mode(int): プロット状態
start_pos(numpy.ndarray): 始点
end_pos(numpy.ndarray): 終点
interference_obj(list): 干渉物
戻り値
planning_result(bool): True / False = 経路生成に成功 / 失敗
elapsed_time(float): 経路生成の処理時間 [sec]
n_waypoint(int): 経由点数(始点と終点を含む)
"""
# 戻り値の初期化
planning_result = False
elapsed_time = 0.0
n_waypoint = 0
# RRTクラスのインスタンスを作成
rrt = RRT()
# 始点から終点までの経路を生成
start_time = time.time()
planning_result = rrt.planning(start_pos, end_pos, interference_obj)
if planning_result:
end_time = time.time()
# 処理時間を計算
elapsed_time = end_time - start_time
# 経由点数を計算
n_waypoint = rrt.pathes.shape[0]
# 生成した経路をファイルに保存
rrt.save()
# RRTアニメーションのインスタンスを作成
rrtAni = RRTAnimation(rrt.strict_min_pos, rrt.strict_max_pos)
# グラフ描画とアニメーション描画で同じ引数としたい
if plot_mode == PLOT_GRAPH: # グラフの描画
result = rrtAni.plot(rrt.pathes, rrt.debug_pathes, interference_obj, dimention)
elif plot_mode == PLOT_ANIMATION: # アニメーションの映画
result = rrtAni.plot_Animation(rrt.pathes, rrt.debug_pathes, rrt.debug_random_pathes, interference_obj, dimention)
return planning_result, elapsed_time, n_waypoint
def rrt_connect_planning(dimention, plot_mode, start_pos, end_pos, interference_obj):
"""
RRT-Connectによる経路生成
パラメータ
dimention(int): 次元数
plot_mode(int): プロット状態
start_pos(numpy.ndarray): 始点
end_pos(numpy.ndarray): 終点
interference_obj(list): 干渉物
戻り値
planning_result(bool): True / False = 経路生成に成功 / 失敗
elapsed_time(float): 経路生成の処理時間 [sec]
n_waypoint(int): 経由点数(始点と終点を含む)
"""
# 戻り値の初期化
planning_result = False
elapsed_time = 0.0
n_waypoint = 0
# RRT-Connectクラスのインスタンスを作成
rrt_connect = RRTConnect()
# 始点から終点までの経路を生成
start_time = time.time()
planning_result = rrt_connect.planning(start_pos, end_pos, interference_obj)
if planning_result:
# 経路生成に成功
end_time = time.time()
# 処理時間を計算
elapsed_time = end_time - start_time
# 経由点数を計算
n_waypoint = rrt_connect.pathes.shape[0]
# 生成した経路をファイルに保存
rrt_connect.save()
# RRT-Connectアニメーションのインスタンスを作成
rrt_connect_animation = RRTConnectAnimation(rrt_connect.strict_min_pos, rrt_connect.strict_max_pos)
# グラフ描画とアニメーション描画で同じ引数としたい
if plot_mode == PLOT_GRAPH: # グラフの描画
result = rrt_connect_animation.plot(rrt_connect.pathes, rrt_connect.start_tree, rrt_connect.end_tree, interference_obj, dimention)
elif plot_mode == PLOT_ANIMATION: # アニメーションの映画
result = rrt_connect_animation.plot_Animation(rrt_connect.pathes, rrt_connect.start_tree, rrt_connect.end_tree, rrt_connect.debug_states, interference_obj, dimention)
return planning_result, elapsed_time, n_waypoint
def rrt_star_planning(dimention, plot_mode, start_pos, end_pos, interference_obj):
"""
RRT*による経路生成
パラメータ
dimention(int): 次元数
plot_mode(int): プロット状態
start_pos(numpy.ndarray): 始点
end_pos(numpy.ndarray): 終点
interference_obj(list): 干渉物
戻り値
planning_result(bool): True / False = 経路生成に成功 / 失敗
elapsed_time(float): 経路生成の処理時間 [sec]
n_waypoint(int): 経由点数(始点と終点を含む)
"""
# 戻り値の初期化
planning_result = False
elapsed_time = 0.0
n_waypoint = 0
# RRT*クラスのインスタンスを作成
rrt_star = RRTStar()
rrt_star.max_iterate = 500
# 始点から終点までの経路を生成
start_time = time.time()
planning_result = rrt_star.planning(start_pos, end_pos, interference_obj)
if planning_result:
# 経路生成に成功
end_time = time.time()
# 処理時間を計算
elapsed_time = end_time - start_time
# 経由点数を計算
n_waypoint = rrt_star.pathes.shape[0]
# 生成した経路をファイルに保存
rrt_star.save()
# RRTアニメーションのインスタンスを作成
rrtStarAni = RRTStarAnimation(rrt_star.strict_min_pos, rrt_star.strict_max_pos)
# グラフ描画とアニメーション描画で同じ引数としたい
print(f"plot_mode = {plot_mode}")
if plot_mode == PLOT_GRAPH: # グラフの描画
result = rrtStarAni.plot(rrt_star.pathes, rrt_star.foler_name_current_tree, rrt_star.file_name_current_tree, rrt_star.count_success, "csv", interference_obj, dimention)
print(f"result = {result}")
return planning_result, elapsed_time, n_waypoint
def path_planning(path_plan, dimention, plot_mode):
"""
経路生成
path_plan(int): 経路生成アルゴリズム番号
dimention(int): 次元数
plot_mode(int): プロット状態
戻り値
planning_result(bool): True / False = 経路生成に成功 / 失敗
elapsed_time(float): 経路生成の処理時間 [sec]
n_waypoint(int): 経由点数(始点と終点を含む)
"""
# 戻り値の初期化
planning_result = False
elapsed_time = 0
n_waypoint = 0
if not (dimention == DIMENTION_2D or dimention == DIMENTION_3D):
# 次元数が2 or 3以外は処理終了
return planning_result, elapsed_time, n_waypoint
# 始点と終点を作成
start_pos = np.ones(dimention).reshape(1, -1) * START_POS
end_pos = np.ones(dimention).reshape(1, -1) * END_POS
# 干渉物の半径を定義
interference_radius = 0.3
if dimention == DIMENTION_2D:
# 円形の干渉物を作成
interference_pos = [[0.8, 0.8], [1.2, 0.8], [1.2, 1.2], [0.8, 1.2]]
interference_obj = [Circle(np.array(pos), interference_radius) for pos in interference_pos]
elif dimention == DIMENTION_3D:
# 球の干渉物を作成
interference_pos = [[0.8, 0.8, 0.8], [1.2, 0.8, 0.8], [1.2, 1.2, 1.2], [0.8, 1.2, 1.2]]
interference_obj = [Ball(np.array(pos), interference_radius) for pos in interference_pos]
else:
# 干渉物はなし
interference_obj = []
if path_plan == PATH_PLANNING_RRT: # RRTによる経路生成
planning_result, elapsed_time, n_waypoint = rrt_planning(dimention, plot_mode, start_pos, end_pos, interference_obj)
elif path_plan == PATH_PLANNING_RRT_CONNECT: # RRT-Connectによる経路生成
planning_result, elapsed_time, n_waypoint = rrt_connect_planning(dimention, plot_mode, start_pos, end_pos, interference_obj)
else: # RRT*による経路生成
if dimention == DIMENTION_2D:
planning_result, elapsed_time, n_waypoint = rrt_star_planning(dimention, plot_mode, start_pos, end_pos, interference_obj)
# 3次元は未作成のため,処理はしない
print(f"planning_result = {planning_result}")
return planning_result, elapsed_time, n_waypoint
def main():
"""
メイン処理
"""
# プロットできる状態
plot_modes = [PLOT_GRAPH, PLOT_ANIMATION, PLOT_NONE]
# 経路生成アルゴリズム
path_plans = [PATH_PLANNING_RRT, PATH_PLANNING_RRT_CONNECT, PATH_PLANNING_RRT_STAR]
# path_plans = [PATH_PLANNING_RRT_STAR, ] # RRT*だけを実施する場合
# 次元数
# dimentions = [DIMENTION_2D, DIMENTION_3D]
dimentions = [DIMENTION_2D, ]
# 全アルゴリズム,全次元,全プロット状態の全組み合わせを実施する
for path_plan in path_plans:
for dimention in dimentions:
for plot_mode in plot_modes:
if plot_mode == PLOT_GRAPH or plot_mode == PLOT_ANIMATION:
# グラフまたはアニメーションを1つ作成
path_planning(path_plan, dimention, plot_mode)
else:
# 経路生成の成功割合や処理時間,経由点数の統計量を計算
planning_results = 0 # 経路生成の成功回数
elapsed_times = [] # 処理時間
n_waypoints = [] # 経由点数
n_path_plan = 30 # 経路生成の回数
for i in range(n_path_plan):
np.random.seed(i) # RRT, RRT-Connect, RRT*で比較するためにシード値を設定する
result, elapsed_time, waypoint = path_planning(path_plan, dimention, plot_mode)
if result:
planning_results += 1
elapsed_times.append(elapsed_time)
n_waypoints.append(waypoint)
# 経路生成の成功割合
epsilon = 1e-2
success_rate = planning_results / n_path_plan
print(f"success_rate = {success_rate}")
if elapsed_times:
# 処理時間の平均,最大,最小,標準偏差を出力
print(f"time ave = {np.mean(elapsed_times)}")
print(f"time max = {np.max( elapsed_times)}")
print(f"time min = {np.min( elapsed_times)}")
print(f"time std = {np.std( elapsed_times)}")
if n_waypoints:
# 経由点の平均,最大,最小,標準偏差を出力
print(f"waypoint ave = {np.mean(n_waypoints)}")
print(f"waypoint max = {np.max( n_waypoints)}")
print(f"waypoint min = {np.min( n_waypoints)}")
print(f"waypoint std = {np.std( n_waypoints)}")
if __name__ == "__main__":
# 本ファイルがメインで呼ばれた時の処理
main()
main.pyを実行すると,RRT/RRT-Connect/RRT* のグラフが作成される.
RRTによる経路生成は下図のようになった.
グラフの見方は以下の通りである.
・水色の星形(左下)データ:経路生成の始点
・緑色の星形(右上)データ:経路生成の終点
・灰色の星形データ:作成したノード
・赤色の線:新規データと最短距離のデータを結んだ線
・緑色の線:最終的な始点から終点までの経路
・灰色の円:干渉物
RRT-Connectによる経路生成は下図のようになった.
グラフの見方は以下の通りである.
・水色の星形(左下)データ:経路生成の始点
・緑色の星形(右上)データ:経路生成の終点
・灰色の星形データ:作成されたノード
・青色の線:終点ツリー
・赤色の線:始点ツリー
・緑色の線:最終的な始点から終点までの経路
・灰色の円:干渉物
RRT* による経路生成は下図のようになった.
グラフの見方は以下の通りである.
・水色の星形(左下)データ:経路生成の始点
・緑色の星形(右上)データ:経路生成の終点
・灰色の星形データ:作成されたノード
・赤色の線:新規データと最短距離のデータを結んだ線
・緑色の線:最終的な始点から終点までの経路
・灰色の円:干渉物
下図はハイパーパラメータRの値を5.0としたときの結果である.
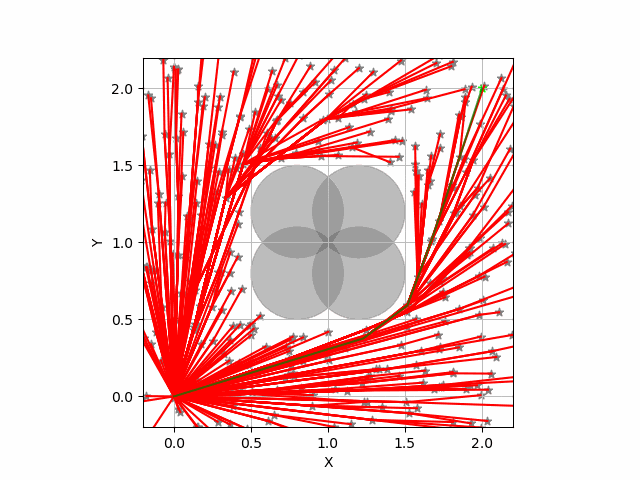
下図はハイパーパラメータRの値を0.5としたときの結果である.
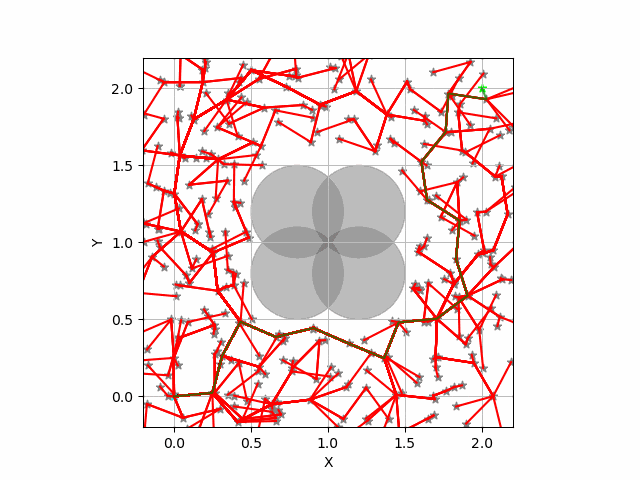
各アルゴリムの性能(統計量)は下表の通りとなった.
| アルゴリズム | 平均処理時間 [sec] | 最小処理時間 [sec] | 最大処理時間 [sec] | 処理時間の標準偏差 [sec] | 平均経由点数 | 最小経由点数 | 最大経由点数 | 経由点数の標準偏差 |
|---|---|---|---|---|---|---|---|---|
| RRT | 0.00575 | 0.00308 | 0.01286 | 0.00206 | 17.5 | 16.0 | 20.0 | 1.3 |
| RRT-Connect | 0.00204 | 0.00111 | 0.00314 | 0.00052 | 16.9 | 15.0 | 20.0 | 1.1 |
| RRT*(R=0.5) | 0.25073 | 0.22355 | 0.28713 | 0.01645 | 18.8 | 16.0 | 23.0 | 1.9 |
| RRT*(R=5.0) | 2.65289 | 2.40563 | 2.85733 | 0.09759 | 6.9 | 5.0 | 9.0 | 0.9 |
上表から本結果に関して,以下のことが言える.
・RRT* はハイパーパラメータRを大きくすると処理時間は増加するが,経由点数が減少するため,最適な経路(距離が最小)を作成できる.
おわりに
本記事では,Pythonを使用して,下記内容を実装しました.
・2次元空間で,円形の干渉物を回避する RRT* による経路生成
・RRT/RRT-Connect/RRT* の性能を評価した
次記事では,下記内容を実装していきます.
・3次元空間で,球の干渉物を回避する RRT* による経路生成
(https://qiita.com/haruhiro1020/items/de9fb322dce87588d48d)