はじめに
私がロボットに関して興味を持っており,ロボットの経路を作成したいと思ったところ,RRT (Rapidly-exploring Random Tree) と呼ばれる経路生成の手法に辿り着いた.
本記事では,経路生成の古典的手法である RRT (Rapidly-exploring Random Tree) をPythonより,実装してみる.
前記事では,干渉物が存在する空間で,2軸ロボットアームのRRTによる経路生成を実装した.
前記事の内容を下記に記します.
・https://qiita.com/haruhiro1020/items/b42725df00e13ddcb5af
本記事では,探索後のRRTに対してのPruning,Shortcutを実装する.
後ほど,PruningやShortcutに関して説明する.
PruningやShortcutは下記を参考にした.
参考文献:
R.Geraerts "Creating High-quality Paths for Motion Planning.", The International Journal of Robotics Research 2007.
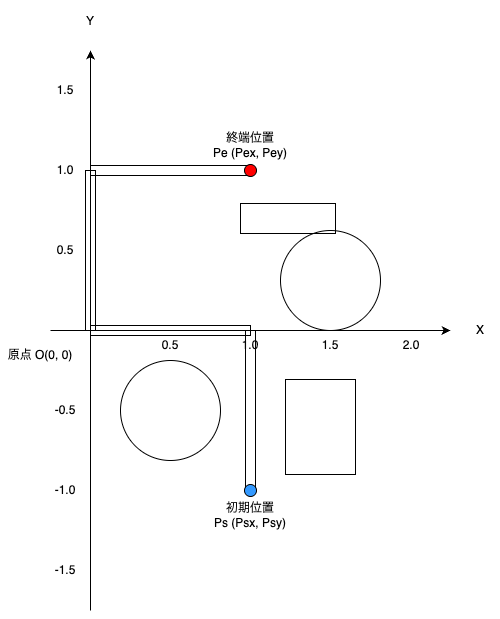
本記事で経路生成する環境は下図の通りである.
青色の点が2軸ロボットアームの初期位置,赤色の点が2軸ロボットアームの目標位置である.
下図環境下で,干渉しない経路を生成するのが,本記事の目標である.
本記事は,前記事で説明したRRT,python-fcl,順運動学,逆運動学を駆使しながら,2軸ロボットアームで,干渉物が存在する環境下での経路生成を実装する.
(https://qiita.com/haruhiro1020/items/b42725df00e13ddcb5af)
本記事で実装すること
・RRTで作成した経路に対しての修正
本記事では実装できないこと(将来実装したい内容)
・3次元空間への拡張
動作環境
・macOS Sequoia (バージョン15.5)
・Python3 (3.10.9)
・Numpy (1.23.5) (数値計算用ライブラリ)
・Matplotlib (3.7.0) (アニメーション作成用ライブラリ)
・python-fcl (0.7.0.8) (干渉判定用ライブラリ)
経路生成手法のまとめ
経路生成手法をまとめた記事を展開いたします.RRT以外の手法も記載してますので,参照いただけますと幸いです.
(https://qiita.com/haruhiro1020/items/000b3287fce082ae4283)
RRTに関して
RRTは経路生成手法である.内容は下記の通りである.
RRTのアルゴリズムを説明する.
参考文献に記載されているRRTのアルゴリズムを抜粋して,下記に記す.
RRTは始点から,終点に向かってどんどんノードを増やしていき,終点との距離がある値以下になったら,経路生成を完了する.
RRTは下図のようなアルゴリズムである.
本記事では,上図のように始点から終点までの経路生成できた,後処理がメインである.
後処理としては,下表の3パターンが論文に記載されている.
| No | アルゴリズム名 | 概要 |
|---|---|---|
| 1 | Pruning | 生成した経路の経由点を始点側から順番に選択し,選択した経由点前後で干渉がなければ,選択した経由点を削除する |
| 2 | Shortcut | 生成した経路の経由点の中からランダムで2点を選択し,2点間で干渉がなければ,2点間の経由点を全部削除する |
| 3 | Partial Shortcut | 生成した経路の経由点の中からランダムで2点を選択し,特定の位置(x, y, z)・姿勢(roll, pitch, yaw)の1要素を選択して,2点間の経由点全部の特定の位置・姿勢の1要素を直線補間し,干渉がなければ,2点間の経由点全部を修正する |
Pruningアルゴリズム
Pruningのアルゴリズムを説明する.
参考文献に記載されているPruningのアルゴリズムを抜粋して,下記に記す.

上記アルゴリズムを説明する.
$N$は,経路を指す.
$2$行目の$|N| - 2$は,経由点数 $- 2$を実施している.経路の中に始点・終点が含まれているため,$-2$を実施することで,始点と終点は選択しないようにしている.
$3$行目の$LP[v_{i}, v_{i+2}] \in C_{free}$は,経路内の$i$要素と$i+2$要素を直線で結び,干渉がなければ$4$行目を実施して,干渉があれば$6$行目を実施する.
$4$行目の$N \leftarrow N / v_{i+1}$は経路$N$から経由点$v_{i+1}$を削除する.
始点側の経由点を順番に削除できるか確認するのが,Pruningである.
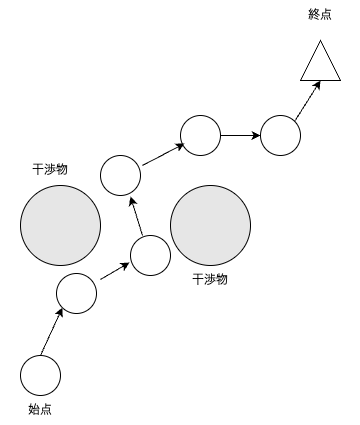
PruningはRRTで作成した経路の始点側の経由点から順番に選択していき,選択した経由点前後で干渉判定を行い,干渉がなければ選択した経由点を削除するアルゴリズムである.
Pruningは下図のようなアルゴリズムである.
$i+1$番目の経由点を選択して,選択した経由点前後で干渉判定する.
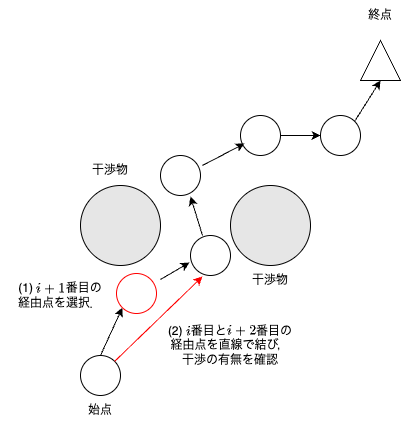
$i+1$番目前後の経由点で干渉なしなら,$i+1$番目の経由点を削除する.
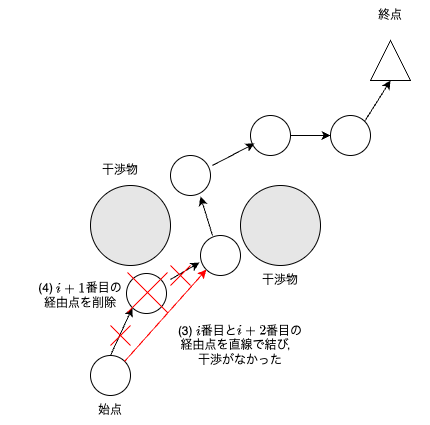
$i+1$番目前後の経由点で干渉ありなら,何もしない(経路は変わらない).

Pruningを実施することで,環境に依存するが経由点数を減らすことができる.
Pruningはランダムで経由点を選択する訳ではないため,Pruning前の経路が同じであれば,Pruning後の経路は一意に決まる.
ソースコードはShortcutも含め,後ほど記載する.
Shortcutアルゴリズム
Shortcutのアルゴリズムを説明する.
参考文献に記載されているShortcutのアルゴリズムを抜粋して,下記に記す.

上記アルゴリズムを説明する.
$\prod$は,経路を指す.
$2$行目の$n \leftarrow |\prod|$は,経由点数である.
$3$行目の$a, b \leftarrow$ two random indices $0 \leq a + 1 < b < n$は,$a$と$b$をランダムで選択するが,制約条件も存在する.$a$と$b$が同じ経由点または隣接した経由点を選択しないように制約条件が存在する.
$7$行目の$LP(\pi_{a}, \pi_{b}) \in C_{free}$は,経路内の$\pi_{a}$要素と$\pi_{b}$要素を直線で結び,干渉がなければ$8$行目を実施する.干渉があれば,$loop$の先頭に戻る.
$8$行目の$\prod \leftarrow \prod' \cup LP(\pi_{a}, \pi_{b}) \cup \prod'''$は経路内の$\pi_{a+1}$から$\pi_{b-1}$の経由点を全部削除する.
Shortcutの最大回数分ループする.
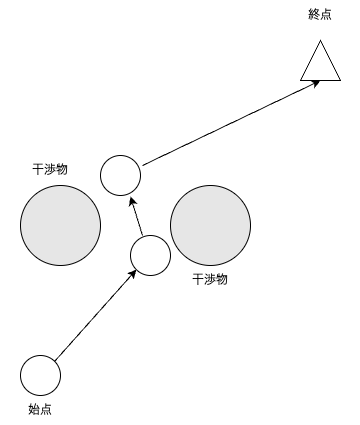
ShortcutはRRTで作成した経路から2点をランダムに選択していき,選択した経由点間で干渉判定を行い,干渉がなければ選択した経由点間の全経由点を削除するアルゴリズムである.
Shortcutは下図のようなアルゴリズムである.
$a$,$b$番目の経由点を選択して,選択した経由点間で干渉判定する.

$a$,$b$番目の経由点間で干渉ありなら,何もしない(経路は変わらない).
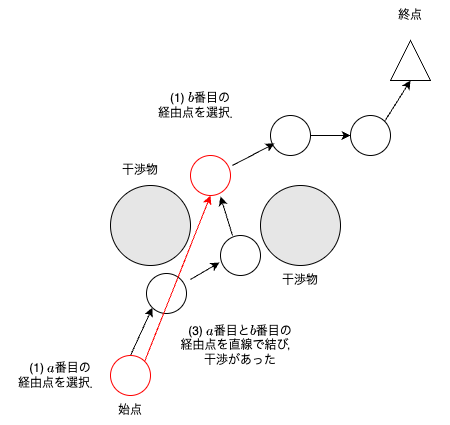
$a$,$b$番目の経由点間で干渉なしなら,$a+1$番目から$b-1$番目の全経由点を削除する.
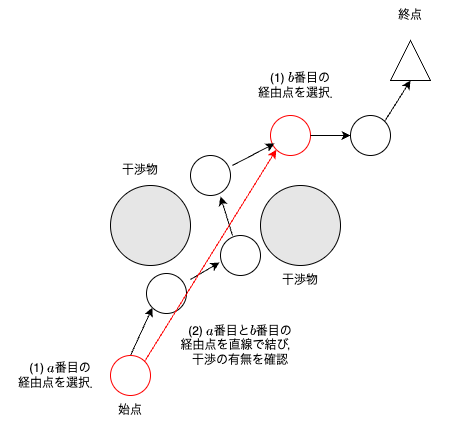
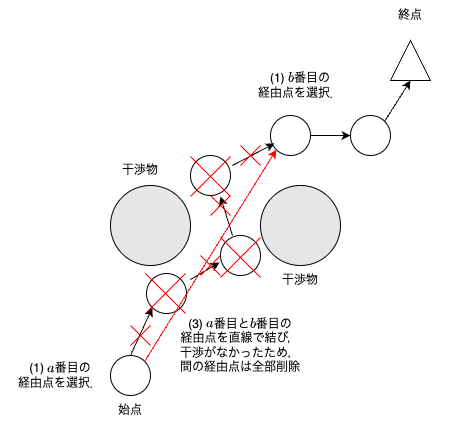
Shortcutを実施することで,環境に依存するが経由点数を減らすことができる.
Shortcutはランダムで経由点を選択するため,Shortcut前の経路が同じであっても,Shortcut後の経路は異なる.ランダムで経由点を選択するため,Shortcut後の経路が最適な経路であるとは限らない.
ソースコードはPartial Shortcutも含め,後ほど記載する.
Partial Shortcutアルゴリズム
Partial Shortcutのアルゴリズムを説明する.
参考文献に記載されているPartial Shortcutのアルゴリズムを抜粋して,下記に記す.

上記アルゴリズムを説明する.
$\prod$は,経路を指す.
$2$行目の$f \leftarrow$ a random degree of freedom は,自由度からランダムで特定の要素を選択して,$f$に代入する.本記事では,経路は2次元$(x, y)$であるため,自由度も$2$である.$f$は$x$または$y$が選択される.
$3$行目の$n \leftarrow |\prod|$は,経由点数である.
$4$行目の$a, b \leftarrow $two random indices $0 \leq a + 1 < b < n$は,$a$と$b$をランダムで選択するが,制約条件も存在する.$a$と$b$が同じ経由点または隣接した経由点を選択しないように制約条件が存在する.
$8$行目の$m \leftarrow |\prod''|$は,経路内の$\pi_{a}$要素と$\pi_{b}$要素内の経由点数を$m$に代入している.$m$には$\pi_{a}$要素と$\pi_{b}$要素の経由点を含んでいる.
$9$行目の for all $\pi_{i}'' \in \prod''$ doは,経路内の$\pi_{a}$要素と$\pi_{b}$要素内の全経由点ループしている.
$10$行目の$\pi_{i}''[f] \leftarrow $INTERPOLATE$(\pi_{0}''[f], \pi_{m-1}''[f], i/(m - 1))$は,経路内の$\pi_{a}$要素と$\pi_{b}$要素内の全経由点の$f$要素を$\pi_{a}$要素と$\pi_{b}$の$f$要素の線形補間(INTERPOLATE)で置き換える.
$12$行目の$\prod'' \in C_{free}$は,$10$行目で置き換えた経路が干渉なければ,$13$行目を実施する.干渉があれば,$loop$の先頭に戻る.
$13$行目の$\prod \leftarrow \prod' \cup \prod'' \cup \prod'''$は経路内の$\pi_{a}$要素と$\pi_{b}$要素内の全経由点を,$10$行目で置き換えた$\prod''$に変更する.
Partial Shortcutの最大回数分ループする.
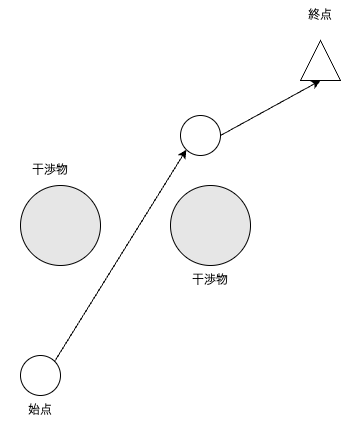
Partial ShortcutはRRTで作成した経路から2点をランダムに選択していき,選択した経由点間のある要素を直線補間で置き換え,干渉がなければ選択した経由点間の全経由点を直線補間に置き換えるアルゴリズムである.
Partial Shortcutは下図のようなアルゴリズムである.
$a$,$b$番目の経由点と自由度から修正したい要素(図では$x$座標)を選択して,選択した経由点間の$x$座標を直線補間する.
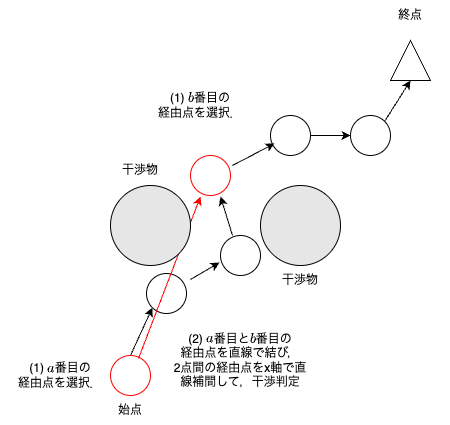
直線補間した$a$番目から$b$番目の全経由点間で干渉ありなら,何もしない(経路は変わらない).
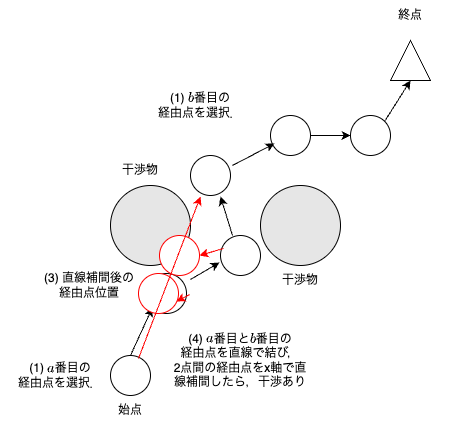
直線補間した$a$番目から$b$番目の全経由点間で干渉なしなら,経路内の$a$番目から$b$番目の全経由点を直線補間した経由点に置き換える.
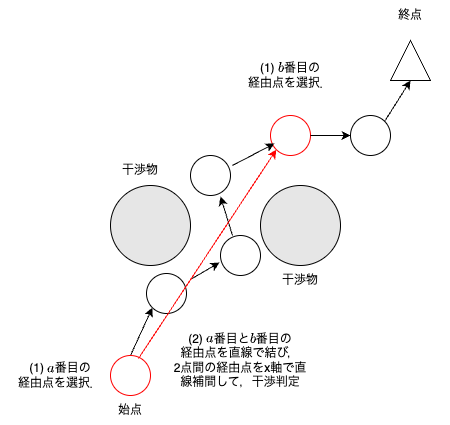

Partial Shortcutによる最終的な経路は下図のようになる.
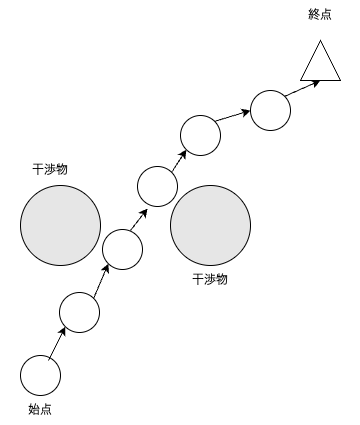
Partial Shortcutを実施することで,経路はスムーズになるが,経由点数は変わらない.
経由点数を減らすためには,Partial Shortcut後の経路に対して,Pruningなどを実施した方が良いかもしれない.
後ほど,ソースコードを記載する.
RRTに関するソースコード作成
上記で説明した,Pruning,Shortcut,Partial Shortcutを実装する.
始点から終点までの経路生成 (Pruning + Shortcut + Partial Shortcut)
RRTを定義するソースコードを書きに記す.
本記事では,下記の RRTRobot() クラスで定義したRRTを使用する.
_modify_path()メソッドで,Pruning + Shortcut + Partial Shortcutを実施している.
# 経路生成手法であるRRT (Rapidly-exploring Random Tree) の実装
# ライブラリの読み込み
import numpy as np
import time
import os
import fcl
# 自作モジュールの読み込み
from constant import * # 定数
class Tree:
"""
ツリークラス
プロパティ
_nodes(numpy.ndarray): ノード
_near_node_idx(int): _nodes内の最短ノードを保存している列番号
メソッド
public
nodes(): _nodesプロパティのゲッター
add_node(): ノードの追加
get_near_node(): 最短距離のノードを取得
"""
# 定数の定義
def __init__(self, near_node_idx):
"""
コンストラクタ
"""
# プロパティの初期化
self._nodes = []
self._near_node_idx = near_node_idx
@property
def nodes(self):
"""
_nodesプロパティのゲッター
"""
return self._nodes
def reset(self):
"""
データの初期化
"""
if len(self._nodes) != 0:
# 何かしらのデータが保存
del self._nodes
self._nodes =[]
def add_node(self, node):
"""
ノードの追加
パラメータ
node(numpy.ndarray): ノード
"""
if len(self._nodes) == 0: # 初回だけ実行
self._nodes = node
else:
self._nodes = np.append(self._nodes, node, axis=0)
def _chk_node_exist(self):
"""
ノードが存在するかの確認
"""
if len(self._nodes) == 0:
# 存在しない
raise ValueError("self._nodes is not exist")
def get_near_node(self, pos):
"""
最短距離のノードを取得
パラメータ
pos(numpy.ndarray): 位置
戻り値
min_dist_idx(int): 最短距離のノード番号
"""
# ノードの存在確認
self._chk_node_exist()
# ノードから位置を取得
nodes_pos = self._nodes[:, :self._near_node_idx]
# 差分を計算
difference = nodes_pos - pos
# 距離を計算 (各ノードとの距離を算出するため,引数にaxis=1を与えた)
distance = np.linalg.norm(difference, axis=1)
# 最短距離ノードを取得
min_dist_idx = np.argmin(distance)
return min_dist_idx
def get_near_node_list(self, pos, radius):
"""
ノードと近傍ノードをリストで取得
パラメータ
pos(numpy.ndarray): ノード位置
radius(float): 半径
戻り値
near_node_list(list): 近傍ノードリスト
"""
# ノードの存在確認
self._chk_node_exist()
near_node_list = []
# ツリー内全ノード位置を取得
all_node_pos = self._nodes[:, :self._near_node_idx]
# ノードとツリー内全ノードの差分を計算
difference = all_node_pos - pos
# 差分から距離(ユークリッド距離)を計算
distance = np.linalg.norm(difference, axis=1)
# 距離が一定以内のノードだけを保存
near_node_list = [idx for idx, dist in enumerate(distance) if dist <= radius]
return near_node_list
class RRTRobot:
"""
RRTにロボットを追加したクラス
プロパティ
_pathes(numpy.ndarray): 始点から終点までの経路 (PruningやShortcut済みの経路)
_start_tree(Tree): 始点ツリー
_start_random_tree(Tree): ランダムな位置を保存した始点ツリー
_strict_min_pos(numpy.ndarray): 探索の最小範囲
_strict_max_pos(numpy.ndarray): 探索の最大範囲
_environment(environment.py内のクラス): 経路生成したい環境
_debug(bool): デバッグフラグ (グラフやアニメーションでデータを確認したいかどうか)
_robot(robot.py内のクラス): ロボットクラス
_moving_value(float): 1回あたりの移動量 [rad] or [m]
_before_modify_pathes(numpy.ndarray): PruningやShortcutなどの修正前の経路
_pruning_pathes(numpy.ndarray): Pruning後の経路
_shortcut_pathes(numpy.ndarray): Shortcut後の経路
_partial_shortcut_pathes(numpy.ndarray): Partial Shortcut後の経路
メソッド
public
planning(): 経路生成の実装
pathes(): _pathesプロパティのゲッター
start_tree(): _treeプロパティのゲッター
start_random_tree(): _random_treeプロパティのゲッター
strict_min_pos(): _strict_min_posプロパティのゲッター
strict_max_pos(): _strict_max_posプロパティのゲッター
environment(): _environmentプロパティのゲッター
protected
_reset(): データの初期化
_add_node(): ツリーにノードを追加する
_chk_end_pos_dist(): 終点との距離が一定範囲内であるかの確認
_fin_planning(): 経路生成の終了処理
_calc_new_pos(): 最短ノードからランダムな値方向へ新しいノード(位置)を作成
_strict_planning_pos(): 探索範囲を制限する
_get_random_pos(): ランダムな位置を取得
_line_interference(): 2点間の干渉チェック
_is_interference_pos(): 干渉判定処理
_save(): データの保存
"""
# 定数の定義
# ファイル名の定義
_FILE_NAME_PATHES = "rrt_pathes.csv" # _pathesプロパティを保存するファイル名
_FILE_NAME_START_TREE = "rrt_start_tree.csv" # _start_treeプロパティを保存するファイル名
_FILE_NAME_START_RANDOM_TREE = "rrt_start_random_tree.csv" # _start_random_treeプロパティを保存するファイル名
_FILE_NAME_BEFORE_MODIFY_PATHES = "rrt_before_modify_pathes.csv" # _before_modify_pathesプロパティを保存するファイル名
_FILE_NAME_PRUNING_PATHES = "rrt_pruning_pathes.csv" # _pruning_pathesプロパティを保存するファイル名
_FILE_NAME_SHORTCUT_PATHES = "rrt_shortcut_pathes.csv" # _shortcut_pathesプロパティを保存するファイル名
_FILE_NAME_PARTIAL_SHORTCUT_PATHES = "rrt_partial_shortcut_pathes.csv" # _partial_shortcut_pathesプロパティを保存するファイル名
# 毎処理保存するファイル名の定義
_FILE_NAME_PRUING_EACH_PATHES = "rrt_pruning_each_pathes" # Pruning実施毎の経路を保存
_FILE_NAME_SHORTCUT_EACH_PATHES = "rrt_shortcut_each_pathes" # Shortcut実施毎の経路を保存
_FILE_NAME_PARTIAL_SHORTCUT_EACH_PATHES = "rrt_partial_shortcut_each_pathes" # Partial Shortcut実施毎の経路を保存
# フォルダー名の定義
_FOLODER_NAME_PRUNING = "Pruning" # Pruning結果を保存するフォルダ
_FOLODER_NAME_SHORTCUT = "Shortcut" # Shortcut結果を保存するフォルダ
_FOLODER_NAME_PARTIAL_SHORTCUT = "PartialShortcut" # PartialShortcut結果を保存するフォルダ
# ツリーの要素番号を定義
_NODE_NEAR_NODE_IDX = RRT_NEAR_NODE_IDX # ノード内の最短ノード要素
# 干渉判定の定義
_DEVIDED_DISTANCE_POS = 0.005 # 2点間を分割する際の基準距離 [m]
_DEVIDED_DISTANCE_JOINT = 0.005 # 2点間を分割する際の基準距離 [rad]
_INTERFERENCE_MARGIN = 0.10 # 干渉物とのマージン (最短距離がマージンよりも小さかったら干渉ありとする) [m]
# 探索に関する定義
_MOVING_VALUE_JOINT = 0.1 # 1回の移動量 [rad] (ロボットの関節空間)
_MOVING_VALUE_POS = 0.2 # 1回の移動量 [m] (ロボットの位置空間)
_STRICT_PLANNING_ROB_JOINT = 1.5 # 探索範囲の制限 [rad] (ロボットの関節空間)
_STRICT_PLANNING_ROB_POS = 0.5 # 探索範囲の制限 [m] (ロボットの位置空間)
_TIMEOUT_VALUE = 10 # タイムアウト時間 [second]
_GOAL_SAMPLE_RATE = 0.1 # ランダムな値を取るときに,終点を選択する確率
def __init__(self):
"""
コンストラクタ
"""
self._start_tree = Tree(self._NODE_NEAR_NODE_IDX)
self._start_random_tree = Tree(self._NODE_NEAR_NODE_IDX)
self._pathes = []
self._environment = None
self._debug = False
self._robot = None
self._interpolation = INTERPOLATION.JOINT
self._moving_value = self._MOVING_VALUE_JOINT
# PruningやShortcut関連のプロパティの初期化
self._before_modify_pathes = []
self._pruning_pathes = []
self._shortcut_pathes = []
self._partial_shortcut_pathes = []
# 作成したいフォルダーをリストにまとめる
folder_names = [self._FOLODER_NAME_PRUNING, self._FOLODER_NAME_SHORTCUT, self._FOLODER_NAME_PARTIAL_SHORTCUT]
for folder_name in folder_names:
self._make_folder(folder_name)
def _make_folder(self, folder_name):
"""
フォルダーの作成
パラメータ
folder_name(str): 作成したいフォルダー名
"""
# フォルダーが作成済みでもエラーを出力しないよう,exist_ok=Trueとした.
os.makedirs(folder_name, exist_ok=True)
def _reset_folder(self, folder_name):
"""
フォルダー内のファイルを全削除
パラメータ
folder_name(str): 全削除したいフォルダー名
"""
for entry in os.listdir(folder_name):
full_path = os.path.join(folder_name, entry)
if os.path.isfile(full_path) or os.path.islink(full_path):
os.remove(full_path) # 通常ファイル・シンボリックリンクを削除
@property
def start_tree(self):
"""
_start_treeプロパティのゲッター
"""
return self._start_tree
@property
def start_random_tree(self):
"""
_start_random_treeプロパティのゲッター
"""
return self._start_random_tree
@property
def pathes(self):
"""
_pathesプロパティのゲッター
"""
return self._pathes
@property
def strict_min_pos(self):
"""
_strict_min_posプロパティのゲッター
"""
return self._strict_min_pos
@property
def strict_max_pos(self):
"""
_strict_max_posプロパティのゲッター
"""
return self._strict_max_pos
def _add_node_start_tree(self, pos, random_pos, near_node):
"""
始点ツリーにノードを追加
パラメータ
pos(numpy.ndarray): 位置
random_pos(numpy.ndarray): ランダムな位置
near_node(int): 最短ノード
"""
# _start_treeにノードを追加
node = np.append(pos, near_node).reshape(1, -1)
self._start_tree.add_node(node)
# デバッグ有効の時しか,ランダムなツリーにデータを保存したくない (処理時間の短縮)
if self._debug:
# _start_random_treeにノードを追加
random_node = np.append(random_pos, near_node).reshape(1, -1)
self._start_random_tree.add_node(random_node)
def _reset(self):
"""
データの初期化
"""
self._start_tree.reset()
self._start_random_tree.reset()
if len(self._pathes) != 0:
# 何かしらのデータが保存
del self._pathes
self._pathes = []
if self._environment is not None:
del self._environment
self._environment = None
if self._robot is not None:
del self._robot
self._robot = None
self._interpolation = INTERPOLATION.JOINT
def _set_robot(self, robot, interpolation):
"""
経路生成したいロボット情報を設定
パラメータ
robot(Robot): ロボットクラス
interpolation(int): 補間の種類 (関節補間/位置補間)
"""
self._robot = robot
if interpolation == INTERPOLATION.POSITION:
# 位置空間
self._interpolation = INTERPOLATION.POSITION
self._moving_value = self._MOVING_VALUE_POS
else:
# 関節空間
self._interpolation = INTERPOLATION.JOINT
self._moving_value = self._MOVING_VALUE_JOINT
def planning(self, start_pos, end_pos, environment, robot, interpolation, modification=MODIFICATION.PRUNING_START, debug=False):
"""
経路生成
パラメータ
start_pos(list): 経路生成の始点
end_pos(list): 経路生成の終点
environment(Base2DEnv): 環境
robot(Robot): ロボットクラス
interpolation(int): 補間方法 (関節空間/位置空間)
modification(str): 経路生成後の修正方法 (Pruning/Shortcutなど)
debug(bool): デバッグフラグ
戻り値
result(bool): True / False = 成功 / 失敗
"""
# 処理結果
result = False
# デバッグフラグの更新
self._debug = debug
# データの初期化
self._reset()
# 始点と終点の次元数が一致しているかの確認
start_pos_dim = np.size(start_pos)
end_pos_dim = np.size(end_pos)
if start_pos_dim != end_pos_dim:
# 次元数が異なるので異常
raise ValueError(f"start_pos_dim and end_pos_dim are not matched. start_pos_dim is {start_pos_dim}, end_pos_dim is {end_pos_dim}")
self._dim = start_pos_dim
# 環境を設定
self._environment = environment
# ロボットの設定
self._set_robot(robot, interpolation)
# 始点と終点の干渉判定
if self._interference_pos(start_pos):
# 干渉ありまたは逆運動学の解が求まらない
raise ValueError(f"start_pos is interference. please change start_pos")
if self._interference_pos(end_pos):
# 干渉ありまたは逆運動学の解が求まらない
raise ValueError(f"end_pos is interference. please change end_pos")
# 始点ノードを設定
self._add_node_start_tree(start_pos, start_pos, INITIAL_NODE_NEAR_NODE)
# 探索する範囲を設定
self._strict_planning_pos(start_pos, end_pos)
# 経路生成は一定時間内に終了させる
start_time = time.time()
# 終点までの経路生成が終わるまでループ
while True:
# for _ in range(1000):
# ランダムな値を取得
random_pos = self._get_random_pos(end_pos)
# ランダムな値と最短ノードを計算
near_node = self._start_tree.get_near_node(random_pos)
# 最短ノードの位置
near_node_pos = self._start_tree.nodes[near_node, :self._NODE_NEAR_NODE_IDX]
# 最短ノードからランダムな値方向へ新しいノード(位置)を作成
new_pos = self._calc_new_pos(random_pos, near_node_pos)
# 新規ノードと最短ノード間での干渉判定
is_interference = self._line_interference(new_pos, near_node_pos)
if not is_interference:
# 干渉なしのため,ノードを設定する
self._add_node_start_tree(new_pos, random_pos, near_node)
# 終点との距離が一定範囲内であるかの確認
if self._chk_end_pos_dist(new_pos, end_pos):
# 一定範囲内のため,経路生成の完了
result = True
break
now_time = time.time()
if now_time - start_time >= self._TIMEOUT_VALUE:
# タイムアウト
break
if result:
# 経路生成に成功のため,経路生成の終了処理
self._fin_planning(start_pos, end_pos)
# PathPruningの実施
self._modify_path(modification)
# ファイルに保存する
self._save()
return result
def _modify_path(self, modification):
"""
始点から終点までの経路を修正
パラメータ
modification(str): 経路生成後の修正方法 (Pruning/Shortcutなど)
"""
if modification is None:
# 修正しない
return
# 修正前の経路を保存
self._before_modify_pathes = np.copy(self._pathes)
if modification == MODIFICATION.PRUNING_START:
# 始点からPruning
self._path_pruning_from_start()
elif modification == MODIFICATION.SHORTCUT_NORMAL:
# Shortcut
self._path_shortcut()
elif modification == MODIFICATION.SHORTCUT_PARTIAL:
# Partial Shortcut
self._path_partial_shortcut()
else:
# 異常
raise ValueError(f"modification is abnormal. modification is {modification}")
def _get_shortcut_two_nodes(self):
"""
Shortcutで使用する2つのノードを取得
戻り値
two_nodes(list): 2つのノード
"""
two_nodes = []
# 削除したいノードを2つ選択する
node1 = np.random.randint(0, self._pathes.shape[0] - 1)
node2 = np.random.randint(0, self._pathes.shape[0] - 1)
# 同じノードであれば,ノード選択に戻る
if node1 == node2:
return two_nodes
# node1に小さいノード番号を保存
if node1 > node2:
node1, node2 = node2, node1
# 隣接するノードであれば,ノード選択に戻る (隣接していれば,Shortcutする理由がない)
if node1 + 1 == node2:
return two_nodes
# 2つのノードを保存
two_nodes = [node1, node2]
return two_nodes
def _path_partial_shortcut(self):
"""
Shortcut (経路上に2点を作成して, 干渉なければ2点内のノードを全削除)
self._pathesプロパティにPruning後の経路が保存される
"""
# 要素番号を保存
n_success = 0
continueous_fail = 0 # 連続失敗回数
# 以前保存してある,Pruningファイルを全削除する
self._reset_folder(self._FOLODER_NAME_PARTIAL_SHORTCUT)
# 位置を構成する要素数を取得
n_element = self._pathes.shape[1]
for _ in range(500):
# ループ回数
# if continueous_fail > 20:
# # 連続で失敗したため,これ以上はPartial Shortcutできないと判断
# break
# 位置の中から,1要素をランダムに取得する (全要素を選択する確率は同じ)
element = np.random.randint(0, n_element - 1)
# 削除したいノードを2つ選択する
two_nodes = self._get_shortcut_two_nodes()
if len(two_nodes) != 2:
# ノード選択に失敗したため,ループ処理の先頭に戻る
continueous_fail += 1
continue
# 2点間のデータを全部取得
partial_pathes = self._pathes[two_nodes[0]: two_nodes[1] + 1].copy()
# 2点で変更したい要素データの差分を計算
diff_data = partial_pathes[-1, element] - partial_pathes[0, element]
for i in range(1, partial_pathes.shape[0] - 1):
partial_pathes[i + 1, element] = partial_pathes[0, element] + diff_data * i / partial_pathes.shape[0]
# 変更した経路間での干渉判定
is_collision = False
for i in range(0, partial_pathes.shape[0] - 1):
if self._line_interference(partial_pathes[i], partial_pathes[i + 1]):
# 干渉ありのため,連続失敗回数の更新
is_collision = True
break
if is_collision:
# 干渉あり
continueous_fail += 1
else:
# 干渉なし
self._pathes[two_nodes[0]: two_nodes[1] + 1] = partial_pathes
continueous_fail = 0
# Shortcutの結果を随時ファイル保存
n_success += 1
if self._debug:
# ファイル名の作成
file_name = f"{self._FOLODER_NAME_PARTIAL_SHORTCUT}/{self._FILE_NAME_PARTIAL_SHORTCUT_EACH_PATHES}_{n_success}.csv"
self._save_numpy_data_to_txt(self._pathes, file_name)
# Shortcut後の経路を保存
self._partial_shortcut_pathes = np.copy(self._pathes)
def _path_shortcut(self):
"""
Shortcut (経路上に2点を作成して, 干渉なければ2点内のノードを全削除)
self._pathesプロパティにPruning後の経路が保存される
"""
# 要素番号を保存
n_success = 0
continueous_fail = 0 # 連続失敗回数
# 以前保存してある,Pruningファイルを全削除する
self._reset_folder(self._FOLODER_NAME_SHORTCUT)
for _ in range(100):
# ループ回数
if continueous_fail > 10:
# 連続で失敗したため,これ以上はShortcutできないと判断
break
# 削除したいノードを2つ選択する
two_nodes = self._get_shortcut_two_nodes()
if len(two_nodes) != 2:
# ノード選択に失敗したため,ループ処理の先頭に戻る
continueous_fail += 1
continue
if not self._line_interference(self._pathes[two_nodes[0]], self._pathes[two_nodes[1]]):
# 干渉なしのため,(idx+1)要素を削除 (行列の行を削除するため,axis=0を引数に与える)
self._pathes = np.delete(self._pathes, range(two_nodes[0] + 1, two_nodes[1] - 1), axis=0)
# 連続失敗回数を初期化
continueous_fail = 0
# Shortcutの結果を随時ファイル保存
n_success += 1
if self._debug:
# ファイル名の作成
file_name = f"{self._FOLODER_NAME_SHORTCUT}/{self._FILE_NAME_SHORTCUT_EACH_PATHES}_{n_success}.csv"
self._save_numpy_data_to_txt(self._pathes, file_name)
else:
# 干渉ありのため,連続失敗回数の更新
continueous_fail += 1
# Shortcut後の経路を保存
self._shortcut_pathes = np.copy(self._pathes)
def _path_pruning_from_start(self):
"""
Pruning (経路の経由点を始点方向から順番に削除)
self._pathesプロパティにPruning後の経路が保存される
"""
# 要素番号を保存
idx = 0
count = 0
# 以前保存してある,Pruningファイルを全削除する
self._reset_folder(self._FOLODER_NAME_PRUNING)
# 経由点数分ループする (始点と終点を含まないために,-2をする)
while idx < self._pathes.shape[0] - 2:
# (idx+1)要素前後のノード間で干渉がないかの確認
if not self._line_interference(self._pathes[idx], self._pathes[idx + 2]):
# 干渉なしのため,(idx+1)要素を削除 (行列の行を削除するため,axis=0を引数に与える)
self._pathes = np.delete(self._pathes, idx + 1, axis=0)
else:
# 干渉ありのため,次要素を選択
idx += 1
# Pruningの結果を随時ファイル保存
count += 1
if self._debug:
# ファイル名の作成
file_name = f"{self._FOLODER_NAME_PRUNING}/{self._FILE_NAME_PRUING_EACH_PATHES}_{count}.csv"
self._save_numpy_data_to_txt(self._pathes, file_name)
# Pruning後の経路を保存
self._pruning_pathes = np.copy(self._pathes)
def _line_interference(self, pos1, pos2):
"""
2点間の干渉チェック
パラメータ
pos1(numpy.ndarray): 位置1/関節1
pos2(numpy.ndarray): 位置2/関節2
戻り値
is_interference(bool): True / False = 干渉あり / 干渉なし
"""
is_interference = False
# 差分を計算
difference = pos2 - pos1
# 距離を計算
distance = np.linalg.norm(difference)
if self._interpolation == INTERPOLATION.POSITION:
# 位置空間 (分割時の距離を保存)
devided_dist = self._DEVIDED_DISTANCE_POS
else:
# 関節空間 (分割時の距離を保存)
devided_dist = self._DEVIDED_DISTANCE_JOINT
# 2点間の分割数を算出
n_devided = max(int(distance / devided_dist), 1)
for i in range(n_devided + 1):
direct_pos = i / n_devided * difference
devided_pos = pos1 + direct_pos
if self._interference_pos(devided_pos):
# 干渉あり
is_interference = True
break
return is_interference
def _interference_pos(self, pos):
"""
干渉判定
パラメータ
pos(numpy.ndarray): 位置/関節
戻り値
is_interference(bool): True / False = 干渉あり / 干渉なし
"""
is_interference = False
if self._interpolation == INTERPOLATION.POSITION:
# 位置空間の場合は,逆運動学を計算
try:
thetas = self._robot.inverse_kinematics(pos)
# ロボットの位置を更新
self._robot.update(thetas)
# 干渉判定
if self._environment.is_collision_dist(self._robot.manager, margin=self._INTERFERENCE_MARGIN):
# 干渉あり
is_interference = True
except Exception as e:
# 逆運動学の解が得られないから,干渉ありとする
is_interference = True
else:
# 関節空間
# ロボットの位置を更新
self._robot.update(pos)
# 干渉判定
if self._environment.is_collision_dist(self._robot.manager, margin=self._INTERFERENCE_MARGIN):
# 干渉あり
is_interference = True
return is_interference
def _chk_end_pos_dist(self, pos, end_pos):
"""
終点との距離が一定範囲内であるかの確認
パラメータ
pos(numpy.ndarray): ノード位置
end_pos(numpy.ndarray): 経路生成の終点
戻り値
is_near(bool): True / False = 一定範囲内である / でない
"""
is_near = False
# 距離を計算
dist = np.linalg.norm(end_pos - pos)
# 一定範囲内であるかの確認
if dist <= self._moving_value:
if not self._line_interference(pos, end_pos):
# 干渉しない
is_near = True
return is_near
def _fin_planning(self, start_pos, end_pos):
"""
経路生成の終了処理
パラメータ
start_pos(list): 経路生成の始点
end_pos(list): 経路生成の終点
"""
# 始点から終点までの経路に関係するノードを選択
revers_path = end_pos.reshape(1, -1)
near_node = -1
while True:
# 終点から始点方向へノードを取得
node = self._start_tree.nodes[near_node]
pos = node[:self._NODE_NEAR_NODE_IDX].reshape(1, -1)
# 浮動小数型になっているので,整数型に型変換
near_node = int(node[self._NODE_NEAR_NODE_IDX])
revers_path = np.append(revers_path, pos, axis=0)
if near_node == INITIAL_NODE_NEAR_NODE:
# 始点ノードまで取得できたため,処理終了
break
# 経路が終点からの順番になっているため,始点から終点とする
self._pathes = revers_path[::-1]
# ツリーに終点を追加 (要素番号を指定するため -1)
self._add_node_start_tree(end_pos, end_pos, self._start_tree.nodes.shape[0] - 1)
def _calc_new_pos(self, random_pos, near_node_pos):
"""
最短ノードからランダムな値方向へ新しいノード(位置)を作成
パラメータ
random_pos(numpy.ndarray): ランダムな位置
near_node_pos(numpy.ndarray): 最短ノード位置
戻り値
new_pos(numpy.ndarray): 新しいノード
"""
# 方向を計算
direction = random_pos - near_node_pos
# 方向の大きさを1にする
norm_direction = direction / (np.linalg.norm(direction) + EPSILON)
# 新しいノードを作成
new_pos = near_node_pos + norm_direction * self._moving_value
return new_pos
def _strict_planning_pos(self, start_pos, end_pos):
"""
探索範囲を制限する
パラメータ
start_pos(numpy.ndarray): 始点
end_pos(numpy.ndarray): 終点
"""
all_pos = np.array([start_pos, end_pos])
# 各列の最大/最小値を取得
min_pos = np.min(all_pos, axis=0)
max_pos = np.max(all_pos, axis=0)
if self._interpolation == INTERPOLATION.POSITION:
# 位置空間の探索
strict_planning_pos = self._STRICT_PLANNING_ROB_POS
self._strict_min_pos = min_pos - strict_planning_pos
self._strict_max_pos = max_pos + strict_planning_pos
else:
# 関節空間の探索
strict_planning_pos = self._STRICT_PLANNING_ROB_JOINT
self._strict_min_pos = min_pos - strict_planning_pos
self._strict_max_pos = max_pos + strict_planning_pos
# self._strict_min_pos = np.ones(self._dim) * np.pi * -1
# self._strict_max_pos = np.ones(self._dim) * np.pi
# print(f"self._strict_min_pos = {self._strict_min_pos}")
# print(f"self._strict_max_pos = {self._strict_max_pos}")
def _get_random_pos(self, target_pos):
"""
ランダムな位置を取得
パラメータ
target_pos(numpy.ndarray): 目標点
戻り値
random_pos(numpy.ndarray): ランダムな位置
"""
# 乱数を取って,目標点を選択するかランダムを選択するか
select_goal = np.random.rand()
if select_goal < self._GOAL_SAMPLE_RATE:
# 目標点を選択s
random_pos = target_pos
else:
random_pos = np.random.uniform(self._strict_min_pos, self._strict_max_pos)
return random_pos
def _save(self):
"""
生成した経路をファイル保存
"""
if self._debug:
# 始点から終点までの修正済みの経路をファイル保存
self._save_numpy_data_to_txt(self._pathes, self._FILE_NAME_PATHES)
# 始点のツリーを保存
self._save_numpy_data_to_txt(self._start_tree.nodes, self._FILE_NAME_START_TREE)
# 始点のランダムツリーを保存
self._save_numpy_data_to_txt(self._start_random_tree.nodes, self._FILE_NAME_START_RANDOM_TREE)
# 修正前の始点から終点までの経路を保存
self._save_numpy_data_to_txt(self._before_modify_pathes, self._FILE_NAME_BEFORE_MODIFY_PATHES)
# Pruning後の経路を保存
self._save_numpy_data_to_txt(self._pruning_pathes, self._FILE_NAME_PRUNING_PATHES)
#
self._save_numpy_data_to_txt(self._shortcut_pathes, self._FILE_NAME_SHORTCUT_PATHES)
self._save_numpy_data_to_txt(self._partial_shortcut_pathes, self._FILE_NAME_SHORTCUT_PATHES)
def _save_numpy_data_to_txt(self, data, file_name):
"""
Numpyデータをテキストファイルに保存
パラメータ
data(numpy.ndarray): ファイル保存したいデータ
file_name(str): 保存したいファイル名
"""
# 引数の確認
if len(data) == 0:
# データが存在しないため,処理終了
return
if not file_name:
# ファイル名が存在しないため,処理終了
return
np.savetxt(file_name, data)
干渉判定用ライブラリ python-fcl に関して
pythonn-fcl の使い方に関して
python-fclの使い方は下記に記載したため,割愛する.
(https://qiita.com/haruhiro1020/items/d364e4c56b1570e1423a)
経路生成の環境に関して
経路生成したい環境は下図を想定している.
青色の点が2軸ロボットアームの初期位置,赤色の点が2軸ロボットアームの目標位置である.
環境内の干渉物の情報は下表の通りである.
| 干渉物名 | 中心点 [m] | 情報1 [m] |
|---|---|---|
| 円1 | $(x, y, z) = (0.5, -0.5, 0.0)$ | 半径 $0.3$ |
| 円2 | $(x, y, z) = (1.5, 0.3, 0.0)$ | 半径 $0.3$ |
| 長方形1 | $(x, y, z) = (1.4, -0.6, 0.0)$ | 箱の長さ$(x, y, z) = (0.4, 0.6, 0.0)$ |
| 長方形2 | $(x, y, z) = (1.2, 0.7, 0.0)$ | 箱の長さ$(x, y, z) = (0.6, 0.2, 0.0)$ |
本環境を定義するソースコード (environment.py)
経路生成したい環境を定義するソースコードは前記事(https://qiita.com/haruhiro1020/items/b42725df00e13ddcb5af) で記載したため,割愛する.
前記事の Robot2DEnv() クラスで定義した環境を使用する.
姿勢を定義するソースコード (rotation.py)
姿勢(回転行列)を定義するソースコードは前記事(https://qiita.com/haruhiro1020/items/b42725df00e13ddcb5af) で記載したため,割愛する.
前記事の MyRotation() クラスで定義した姿勢を使用する.
定数を定義するソースコード (constant.py)
定数を定義するソースコードを下記に記載する.
# 複数ファイルで使用する定数の定義
from enum import Enum
from enum import auto
# 次元数を定義
DIMENTION_NONE = -1 # 未定義
DIMENTION_2D = 2 # 2次元
DIMENTION_3D = 3 # 3次元
# ノードの最短ノード要素とコスト要素を定義
RRT_NEAR_NODE_IDX = -1 # RRTでの最短ノード要素
RRT_CONNECT_NEAR_NODE_IDX = -1 # RRT-Connectでの最短ノード要素
RRT_STAR_NEAR_NODE_IDX = -3 # RRT*での最短ノード勝訴
RRT_STAR_COST_IDX = -2 # RRT*でのコスト要素
RRT_STAR_RADIUS_IDX = -1 # RRT*での半径要素
INFORMED_RRT_STAR_NEAR_NODE_IDX = -3 # Informed RRT*での最短ノード勝訴
INFORMED_RRT_STAR_COST_IDX = -2 # Informed RRT*でのコスト要素
INFORMED_RRT_STAR_RADIUS_IDX = -1 # Informed RRT*での半径要素
# 回転軸
ROTATION_X_AXIS = "rot_x" # x軸周りに回転
ROTATION_Y_AXIS = "rot_y" # y軸周りに回転
ROTATION_Z_AXIS = "rot_z" # z軸周りに回転
# ツリーの初期ノードの親ノード
INITIAL_NODE_NEAR_NODE = -1 # 初期ノードに親ノードが存在しないから-1
# 補間時の分割する時の距離
DEVIDED_DISTANCE_JOINT = 0.1 # 関節補間時の距離 [rad]
DEVIDED_DISTANCE_POSIION = 0.1 # 位置補間時の距離 [m]
# 干渉物の名称を定義
class INTERFERENCE(Enum):
"""
干渉物の名称を定義
"""
NONE = "" # 未定義
# 2次元の干渉物 ↓
CIRCLE = "circle" # 円形の干渉物
RECTANGLE = "rectangle" # 長方形の干渉物
LINE2D = "line2D" # 2次元の直線
# 2次元の干渉物 ↑
# 3次元の干渉物 ↓
BALL = "ball" # 球の干渉物
CUBOID = "cuboid" # 直方体の干渉物
LINE3D = "line3D" # 3次元の直線
# 3次元の干渉物 ↑
# 0割を防ぐための定数
EPSILON = 1e-6
# プロットする時にグラフ(静止画)とするかアニメーションを定義
PLOT_NONE = 20 # プロットしない
PLOT_GRAPH = 21 # グラフ
PLOT_ANIMATION = 22 # アニメーション
# 補間方法の定義
class INTERPOLATION(Enum):
"""
補間方法
"""
JOINT = 10 # 関節補間
POSITION = auto() # 位置補間
LINEAR = auto() # 直線補間
CUBIC = auto() # 3次補間
QUINTIC = auto() # 5次補間
# RRTで作成した経路の修正方法を定義
class MODIFICATION(Enum):
"""
修正方法
"""
# 修正方法が単一
PRUNING_START = "pruning_start" # 始点からのPruning
SHORTCUT_NORMAL = "shortcut" # Shortcut
SHORTCUT_PARTIAL = "partial_shortcut" # Partial Shortcut
2軸ロボットアームに関して
2軸ロボットアームは下図を想定している.
リンク1はz軸に$\theta_{1}$回転し,リンク2はz軸に$\theta_{2}$回転する,2軸ロボットアームを考えている (z軸とは,下図のx軸とy軸との直角な方向であり,見ている図はz軸から見ている図である).
$\theta_{1} = 0$かつ$\theta_{2} = 0$の時,ロボットの手先位置は$(x, y ) = (l_{1} + l_{2}, 0)$となる.

2軸ロボットアームの順運動学 (関節角度から手先位置を算出する)
2軸ロボットアームの順運動学は下記に記載したため,割愛する.
・https://qiita.com/haruhiro1020/items/4529e648161beac7754f
2軸ロボットアームの逆運動学 (手先位置から関節角度を算出する)
2軸ロボットアームの逆運動学は下記に記載したため,割愛する.
・https://qiita.com/haruhiro1020/items/9416bea4b5b0757f4f36
2軸ロボットアームの直方体化
2軸ロボットアームを干渉判定させるためには,各リンクを直方体と考える必要がある.
各リンクの直方体としての値は下表のように考えている.
| リンク名 | x [m] | y [m] | z [m] |
|---|---|---|---|
| 1 | $l_{1}(1.0)$ | 0.04 | 0.04 |
| 2 | $l_{2}(1.0)$ | 0.04 | 0.04 |
2軸ロボットアームを定義するソースコード (robot.py)
2軸ロボットアームを定義するソースコードは前記事(https://qiita.com/haruhiro1020/items/b42725df00e13ddcb5af) で記載したため,割愛する.
前記事の Robot2DoF() クラスで定義したロボットを使用する.
経路生成のアニメーション
上記でRRTの実装をしたが,想定通りに動いているかの確認が必要なため,アニメーションを作成して確認する.
Pruning,Shortcut,Partial Shortcutのアニメーションを作成する.
# ロボットのアニメーションを実施
# ライブラリの読み込み
import numpy as np # 数値計算
import matplotlib.pyplot as plt # 描画用
import matplotlib.animation as ani # アニメーション用
import matplotlib.patches as patches # 2次元形状の描画
# 自作モジュールの読み込み
from constant import * # 定数
class RobotAnimation:
"""
ロボットのアニメーション作成
プロパティ
_figure: 描画枠
_axis: 描画内容
publicメソッド (全てのクラスから参照可能)
plot_Animation(): アニメーション作成
protectedメソッド (自クラスまたは子クラスが参照可能)
_reset2D(): 2次元データのリセット
"""
# 定数の定義
_ANIMATION_NAME = "robot_animation.gif"
_PLOT_NAME = "robot_plot.gif"
def __init__(self):
"""
コンストラクタ
"""
pass
def _reset2D(self):
"""
2次元データのリセット
"""
self._figure = plt.Figure()
self._axis = self._figure.add_subplot(111)
# X/Y軸に文字を記載
self._axis.set_xlabel("X")
self._axis.set_ylabel("Y")
self._axis.grid()
self._axis.set_aspect("equal")
def _plot_circle(self, x, y, radius):
"""
円の描画
パラメータ
x(float): 中心点 (x)
y(float): 中心点 (y)
radius(float): 半径
"""
circle = patches.Circle((x, y), radius, color="gray", alpha=0.5)
self._axis.add_patch(circle)
def _plot_rectangle(self, x, y, width, height, angle):
"""
長方形の描画
パラメータ
x(float): 左下隅の座標 (x)
y(float): 左下隅の座標 (y)
width(float): 幅
height(float): 高さ
angle(float): 角度 [deg]
"""
rect = patches.Rectangle((x, y), width, height, angle=angle, color="gray", alpha=0.5)
# 長方形を軸に追加
self._axis.add_patch(rect)
def _plot_environment(self, environment):
"""
アニメーション作成
パラメータ
environment(Robot2DEnv): 経路生成時の環境
"""
if environment is None:
# 環境がないため,何もしない
return
for name, datas in environment.interferences.items():
# 干渉物の名称
if name == INTERFERENCE.CIRCLE:
# 円
for x, y, radius in datas:
self._plot_circle(x, y, radius)
elif name == INTERFERENCE.RECTANGLE:
# 長方形
for x, y, center_x, center_y, angle in datas:
# 中心点から左隅の点に移動させるために,-x/2,-y/2を実施
self._plot_rectangle(center_x - x / 2, center_y - y / 2, x, y, angle)
else:
# 何もしない
pass
def plot_Animation(self, robot, all_link_thetas, environment, anime_file_name=""):
"""
アニメーション作成
パラメータ
robot(Robot2DoF): ロボットクラス
all_link_thetas(numpy.ndarray): 全リンクの回転角度
environment(Robot2DEnv): 経路生成時の環境
anime_file_name(str): アニメーションのファイル名
"""
# 引数の確認
if all_link_thetas.size == 0:
raise ValueError(f"all_link_thetas's size is abnormal. all_link_thetas's size is {all_link_thetas.size}")
# データをリセットする
self._reset2D()
# 全画像を保存する
imgs = []
# 環境の描画
self._plot_environment(environment)
# 手先位置の軌跡を保存
position_trajectory = np.zeros((all_link_thetas.shape[0], DIMENTION_2D))
# 始点と終点をプロット
# 始点位置を取得
start_pos = robot.forward_kinematics(all_link_thetas[0])
start_image = self._axis.scatter(start_pos[0], start_pos[1], color="cyan")
end_pos = robot.forward_kinematics(all_link_thetas[-1])
end_image = self._axis.scatter(end_pos[0], end_pos[1], color="red")
# 軌道生成
for i, thetas in enumerate(all_link_thetas):
path_images = []
# 順運動学により,全リンク (ベースリンク, リンク1,手先位置) の位置を計算
all_link_pos = robot.forward_kinematics_all_link_pos(thetas)
# 線プロット
image = self._axis.plot(all_link_pos[:, 0], all_link_pos[:, 1], color="blue")
path_images.extend(image)
# 点プロット
image = self._axis.scatter(all_link_pos[:, 0], all_link_pos[:, 1], color="black", alpha=0.5)
path_images.extend([image])
# 手先位置を保存
position_trajectory[i] = all_link_pos[-1]
# 手先位置の軌跡をプロット
image = self._axis.plot(position_trajectory[:i + 1, 0], position_trajectory[:i + 1, 1], color="lime")
path_images.extend(image)
# 始点と終点の画像を保存
path_images.extend([start_image])
path_images.extend([end_image])
# 画像を1枚にまとめて保存
imgs.append(path_images)
# アニメーション作成
animation = ani.ArtistAnimation(self._figure, imgs)
if anime_file_name:
# ファイル名が存在する
animation.save(anime_file_name, writer='imagemagick')
else:
# ファイル名が存在しない
animation.save(self._ANIMATION_NAME, writer='imagemagick')
plt.show()
RRTの経路生成およびアニメーションを実施するメイン処理は下記の通りである.
# メイン処理
# ライブラリの読み込み
import numpy as np # 数値計算
import matplotlib.pyplot as plt # 描画
# 自作モジュールの読み込み
from constant import * # 定数
from robot import Robot2DoF # ロボットクラス
from animation import RobotAnimation # ロボットのアニメーション
from rrt import RRTRobot # 経路生成
from environment import Robot2DEnv # 経路生成の環境
def main():
"""
メイン処理
"""
# 2軸ロボットのリンク長
links = np.array([1.0, 1.0])
# 2軸ロボットのインスタンスを作成
robot = Robot2DoF(links)
# 始点
start_pos = np.array([1.0, -1.0])
# 終点
end_pos = np.array([1.0, 1.0])
try:
# 始点と終点の逆運動学
start_theta = robot.inverse_kinematics(start_pos)
end_theta = robot.inverse_kinematics(end_pos)
except Exception as e:
# 逆運動学の解が存在しない (始点または終点が異常な値)
raise ValueError(f"please start_pos or end_pos is change. pos is singularity")
# RRTのデバッグフラグ
debug = True
# 経路の修正方法
modification = MODIFICATION.PRUNING_START # Pruning
# modification = MODIFICATION.SHORTCUT_NORMAL # Shortcut
# modification = MODIFICATION.SHORTCUT_PARTIAL # Partial Shortcut
np.random.seed(1)
# 環境
environment = Robot2DEnv()
# 補間の種類 (位置空間/関節空間)
interpolations = [INTERPOLATION.JOINT, INTERPOLATION.POSITION]
interpolations = [INTERPOLATION.POSITION, ]
for interpolation in interpolations:
# RRTによる経路生成
rrt = RRTRobot()
if interpolation == INTERPOLATION.POSITION:
# 位置空間での経路生成の実行
planning_result = rrt.planning(start_pos, end_pos, environment, robot, interpolation, modification=modification, debug=debug)
else:
# 関節空間での経路生成の実行
planning_result = rrt.planning(start_theta, end_theta, environment, robot, interpolation, modification=modification, debug=debug)
print(f"planning_result = {planning_result}")
if not planning_result:
# 経路生成の失敗
return
# アニメーション作成
robotAnime = RobotAnimation()
if interpolation == INTERPOLATION.POSITION:
# 位置空間による RRT 経路生成
# 逆運動学による関節を取得
thetas = np.zeros((rrt.pathes.shape[0], DIMENTION_2D))
for i, pos in enumerate(rrt.pathes):
# 逆運動学
theta = robot.inverse_kinematics(pos)
thetas[i] = theta
# ファイル名
file_name = "rrt_robot_pos_anime.gif"
robotAnime.plot_Animation(robot, thetas, environment, file_name)
else:
# 関節空間による RRT 経路生成
# ファイル名
file_name = "rrt_robot_joint_anime.gif"
robotAnime.plot_Animation(robot, rrt.pathes, environment, file_name)
if __name__ == "__main__":
# 本ファイルがメインで呼ばれた時の処理
main()
main.pyを実行すると,"gif"が作成される.
RRTによる経路生成は下図のようになった.
アニメーションの見方は以下の通りである.
・水色の星形(左下)データ:経路生成の始点
・緑色の星形(右上)データ:経路生成の終点
・黒色の星形データ:RRTで生成された経由点
・青色の球データ:新規データ
・赤色の星形データ:乱数データ
・赤色の線:乱数データと最短距離のデータを結んだ線
・緑色の線:最終的な始点から終点までの経路
・灰色の球:干渉物
上アニメーションより,"Pruning","Shortcut","Partial Shortcut"を実装できていることが確認できた.
また,以下感想を思った.
・PruningやShortcutで経由点が削除されているため,経路がさらに良くなった
・Pruningは始点に近い経由点から順番に削除していくが,終点に近い経由点から順番に削除したり,RRT-Connectのように始点と終点の両方から削除していくなどの改善に余地がある
・Shortcutはランダム要素が強いので,点の選択方法を改善する余地がある(具体的には,干渉物との距離に応じて,選択する確率を変えるなど)
・Partial Shortcutもランダム要素が強い.今回のアニメーションでは綺麗(スムーズ)な経路となっているが,ランダムなためスムーズではない経路にもなる
・Partial Shortcutは経由点削減できないため,Partial Shortcut後にPruningを実行するのが良いかもしれない
次回は,"Pruning","Shortcut","Partial Shortcut"を組み合わせた経路生成を実装したい.また,経由点の削除中のアニメーションを作成することにって,より良い経由点の削除方法を考えることができるかもしれないため,アニメーションを作成して,より良い案を考えてみる.
おわりに
本記事では,Pythonを使用して,下記内容を実装しました.
・2次元空間で,RRTによる経路生成後にPruning,Shortcut,Partial Shortcutを実装
次記事では,下記内容を実装していきます.
・3次元空間で,RRTによる経路生成後にPruning,Shortcut,Partial Shortcutを実装
・2次元空間で,RRTによる経路生成後にPruning,Shortcut,Partial Shortcutの組み合わせを実装
・Pruning,Shortcut,Partial Shortcut途中のアニメーション作成