ElasticNetの概要とパラメータチューニングについて

はじめに

本記事では、機械学習の回帰手法の一つである、ElasticNetの紹介、およびそのパラメータチューニングの方法について解説します。

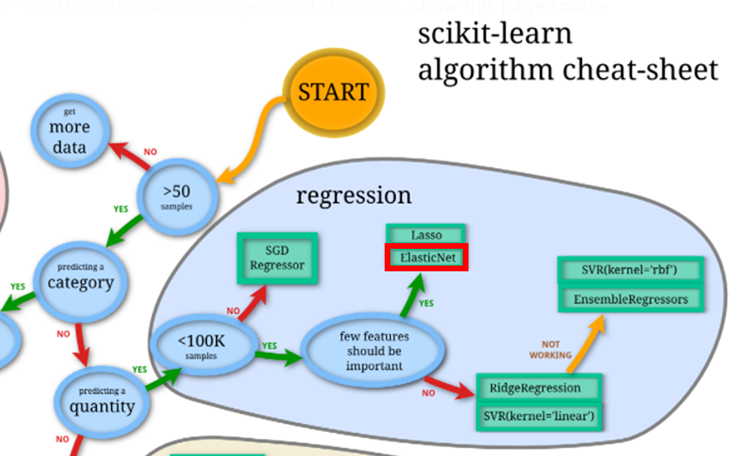
Scikit-Learnのチートシートにも登場する重要な手法なので、回帰を実務で活用したい方はぜひご一読頂けばと思います！

過学習と正則化

ElasticNetの前提知識として必要な、過学習と正則化について解説します

・過学習

機械学習を実際に活用する上で、大きな障害となるのが過学習です。

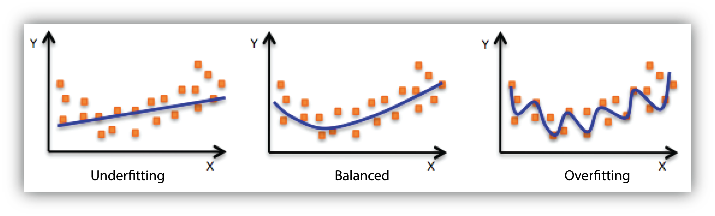
過学習とは、「学習データに過剰に合わせ込んだ状態」を表しており、これにより未知データに対する推定性能が落ちることが、実用上での弊害となります。

※下の図はAWSにおける過学習（Overfitting）の説明です。

・正則化

過学習を防ぐための代表的な対応手法が、正則化です。

機械学習は、一般的に学習データに対する損失関数を最小化するように学習しますが、
これだけでは細かくフィッティングした複雑なモデルが生成され、過学習が起こります。

そこで、損失関数にモデルの複雑さを表す指標（正則化項）を加え、これを最小化するよう学習すれば、
性能と複雑さ、すなわち過学習と未学習のバランスを取った学習が実現できます。

過学習と正則化については、以下の記事で詳説しているので、ご参照頂ければと思います。

正則化とElasticNet

詳しくは上記記事をご参照頂ければと思いますが、正則化には大きく分けてL1正則化とL2正則化があります。

L1、L2それぞれの正則化項は、以下のように表されます。

L2正則化\;:\;\alpha||\boldsymbol{w}||^2=\displaystyle{\sum_{j=1}^{D}w_{j}^{2}}\\
L1正則化\;:\;\alpha||\boldsymbol{w}||_1=\displaystyle{\sum_{j=1}^{D}|w_{j}|}

・線形回帰とリッジ回帰、ラッソ回帰

上記の式だけだと何のことだか分からないので、実際の機械学習における正則化の活用例である、リッジ回帰とラッソ回帰を紹介します

線形回帰

一般的に線形回帰の式は、

{\hat{y}}=\displaystyle{\sum_{j=1}^{D}w_{j}x_{j}+w_{0}}={\bf \boldsymbol{x}^T\boldsymbol{w}}\\

\left\{\begin{array}{ll}
{\hat{y}}:目的変数の予測値\\
x_j:説明変数(ベクトル表記が\boldsymbol{x})\\
w_j:説明変数の係数(ベクトル表記が\boldsymbol{w})\\
D:説明変数の次元数
\end{array}\right.

で表されます。
このとき、平均二乗誤差は以下の式で表されます
※式を簡単にするためNを掛けています
※j（次元方向）とi（データ数方向）の違いにご注意ください

L=\displaystyle{\sum_{i=1}^{N}(\hat{y}_i-y_i)^2}=\displaystyle{\sum_{i=1}^{N}(\boldsymbol{x_i}^T\boldsymbol{w}-y_i)^2}\\

\left\{\begin{array}{ll}
y_i:目的変数の実測値データ\\
\hat{y}_i:目的変数の予測値データ\\
\boldsymbol{x_i}:説明変数の実測値データ\\
N:データ数
\end{array}\right.

この式は

X=\begin{pmatrix}
\boldsymbol{x_1}^T \\
\boldsymbol{x_2}^T \\
:\\
\boldsymbol{x_N}^T
\end{pmatrix}\\
\boldsymbol{y}=\begin{pmatrix}
y_1 \\
y_2 \\
:\\
y_N
\end{pmatrix}

と置くと、

$$L = (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})$$
で表されます。
上記のLを最小化するようなwの組合せを定めるのが、線形回帰の学習となります。

この線形回帰に正則化項を追加して過学習に強くしたアルゴリズムが、リッジ回帰とラッソ回帰です

リッジ回帰

元々のLに、L2正則化項
$$\alpha||\boldsymbol{w}||^2$$
を足し、

L=\underset{\Large損失関数}{\underline{\displaystyle{(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})}}}+\displaystyle\underset{\Large正則化項}{\underline{\alpha||\boldsymbol{w}||^2}}

を新たな最小化関数とします

ラッソ回帰

元々のLに、L1正則化項
$$\alpha||\boldsymbol{w}||$$
を足し、

L=\underset{\Large損失関数}{\underline{\displaystyle{(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})}}}+\displaystyle\underset{\Large正則化項}{\underline{\alpha||\boldsymbol{w}||}}

を新たな最小化関数とします。
ラッソ回帰は多くの説明変数の係数が0となる（スパース性を持つ）ため、リッジ回帰と比べてより強い過学習防止効果が得られます。

・リッジ回帰 vs. ラッソ回帰

リッジ回帰とラッソ回帰の実用上での差をまとめると、以下のようになります。
参考

	正則化の手法	メリット	デメリット
リッジ回帰	L2正則化	・少ない学習データ数でも機能する ・共線性があっても有用な変数が削除されない	・特徴量を絞り込めず解釈性、過学習防止効果が低い
ラッソ回帰	L1正則化	・スパースに特徴量を絞り込めるため、解釈性、過学習防止効果が高い	・説明変数の数 > 学習データ数では有効に機能しない ・共線性があるとき、スパース性により真に有用な変数がランダムに消去される事がある

・ElasticNet

前述のように、リッジ回帰とラッソ回帰にはそれぞれ長所と短所があります。
この長所と短所をカバーするため、リッジ回帰とラッソ回帰を組み合わせていいとこどりをしようというアルゴリズムが、ElasticNetです。

ElasticNetの最小化関数は、L2、L1正則化項を足し合わせた以下の式となります。

L=\underset{\Large損失関数}{\underline{\displaystyle{(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})}}}+\displaystyle\underset{Ⅼ２正則化項}{\underline{\lambda_2||\boldsymbol{w}||^2}}+\displaystyle\underset{Ⅼ１正則化項}{\underline{\lambda_1||\boldsymbol{w}||}}

上記のLを最小化するようなwの組合せを定めるのが、ElasticNetの学習です。
最終的な**回帰式は説明変数の整数倍の和（線形回帰と同様）**となります。

なお、Scikit-Learnにおいてはスケール合わせのため以下のようにLの式を変形しています

L=\underset{\Large損失関数}{\underline{\displaystyle{\frac{1}{2N} (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})}}}+\displaystyle\underset{\LargeⅬ２正則化項}{\underline{\frac{\alpha(1-l_1)}{2}||\boldsymbol{w}||^2}}+\displaystyle\underset{\LargeⅬ１正則化項}{\underline{\alpha l_1||\boldsymbol{w}||}}\\
\left\{\begin{array}{ll}
N:データ数\\
\alpha:ハイパーパラメータalpha\\
l_1:ハイパーパラメータl1\_ratio
\end{array}\right.

上記の
alpha（L1,L2正則化項の合計値（L2は1/2で正規化））
l1_ratio（L1正則化項の割合）
がハイパーパラメータとして残るので、検証データでの性能が上がるようパラメータチューニングを実施する必要があります。

パラメータチューニングの実装法は後述します

また、l1_ratio=0のときRidge回帰（L1正則化項=0）と、l1_ratio=1のときLasso回帰（L2正則化項=0）と等しくなります。

ElasticNetと他の機械学習による回帰手法

今まで紹介した回帰手法（線形回帰、Ridge、Lasso、Elasticnet）以外にも、機械学習による回帰手法は多数存在します（LightGBM、XGBoost、サポートベクター回帰etc.）
よって

これらと比べてElasticNetは何がいいの？

というのが、実用上の興味として非常に大きいかと思います

・ElasticNetの他の機械学習手法に対するメリット

ElasticNetのメリットを端的に言うと

回帰式が線形である（Ridge回帰、Lasso回帰も同様）

ことに尽きるかと思います。

LightGBMやRBFカーネルのサポートベクター回帰など、多くの回帰アルゴリズムは非線形な手法ですが、ElasticNetは学習（最適化）時に過学習を防ぐための正則化項を加えているのみで、回帰式自体は線形回帰と同様に、説明変数の整数倍の和で表され、線形性が維持されています。

上記により一定の傾きが保証されたシンプルなモデルとなるので、以下のような場合に適していると言えます。

ElasticNetが向いているケース	ElasticNetが向いていないケース
1. ドメイン知識から、線形に近い単調増加が想定される場合 2. 単調増加かつある程度の外挿性能が求められるとき 3. 多少性能を犠牲にしてでも回帰式を明示して説明性を上げたいとき	1. ドメイン知識から、非線形な変化が想定される場合 2. チューニング後の評価指標で非線形手法に大きく劣る場合（非線形が想定される）

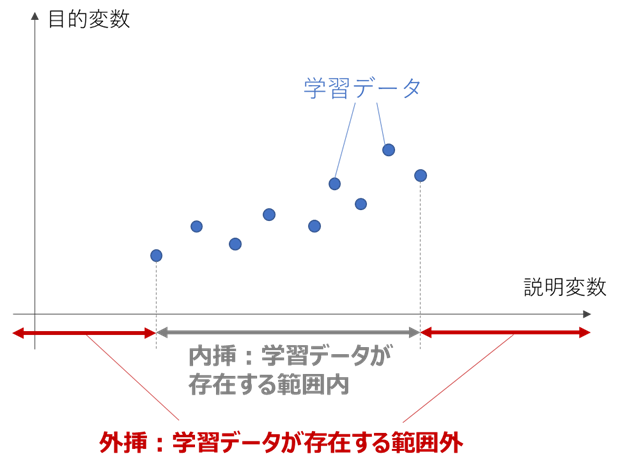
・外挿とElasticNet

向いているケース2に登場する外挿とは、学習データが存在する範囲の外側を表しています。

一般的に機械学習は、内挿と比べ外挿部分の予測性能が極端に低下しますが、
ElasticNetや線形回帰は内挿部分の傾きを維持して外挿部分を予測するため、外挿部分もある程度の予測をできることが多いです。
（もちろん、真値の傾きが外挿部分で急変化する場合は対処不可ですが‥）

逆にランダムフォレスト回帰やLightGBM、XGBoostなどの決定木ベースの手法は、外挿部分の予測値が一定値となるため、外挿性能が非常に悪い傾向があります。
（参考）

・回帰における線形手法と非線形手法の使い分け

上記のように、線形な手法は外挿に強い、回帰式が明示できて解釈性が高いなどのメリットがあります。

前述のScikit-Learnチートシートでも線形な手法を最初に検討するフローとなっていることから、むやみに非線形な手法を使用せず、まずはシンプルに線形なモデルを構築できないかを検討することが、ひとつの流儀として確立されているようです。

ElasticNetは多くの線形手法（線形回帰、Ridge、Lasso）を内包しているため、線形手法の中でも汎用性が高く、有力な選択肢となります

もちろん、「初手LightGBM」という言葉が示すように、性能やモデルの柔軟性は非線形な手法の方が高い傾向にあり、解釈性に関してもFeature Importanceや後付けのSHAPなどのソリューションが存在するため、一概にどちらが良いとは言えません。

このあたりは、内挿・外挿性能のバランスや解釈性に基づき、実際のデータを見て判断するのがよいかと思います。

ElasticNetとパラメータチューニング

前述のように、ElasticNetはalphaとl1_ratioという2つのハイパーパラメータを持ちます。

過学習を防ぎつつ回帰性能を上げるためには、検証データ（未知データ）での性能が上がるようパラメータチューニングを行う必要があります。

パラメータチューニングに関しては以下の記事で詳説しているので、本記事ではElasticNetにおける実装法を紹介します。

チューニング手順

下図のフロー（こちらの記事と同じ）に基づき、ElasticNetのパラメータチューニングを実装します

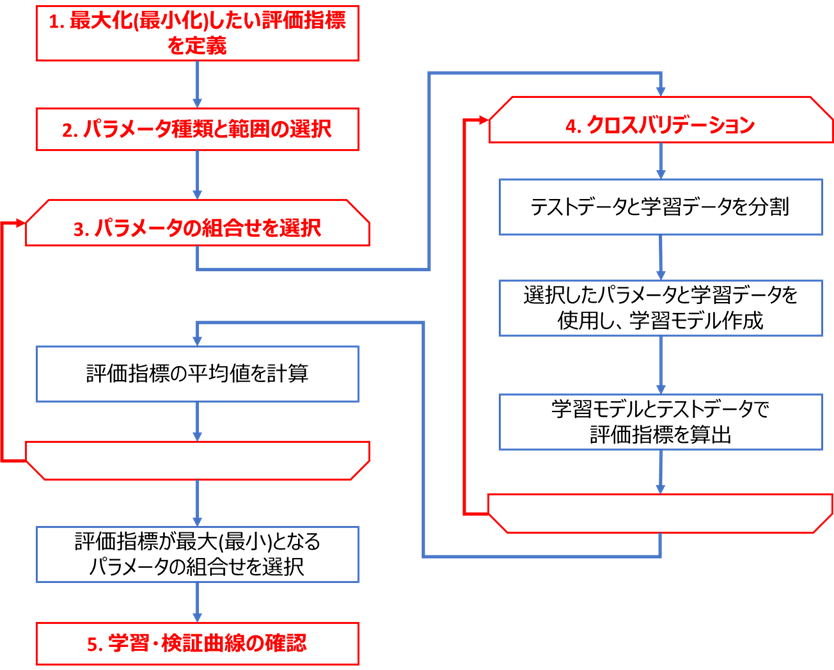
コードはこちらのGitHub（elasticnet_tuning_tutorials.py）にもアップロードしております。

実装に必要な環境整備

ライブラリ

チューニングの実装に必要なライブラリ等をインストールします。
私の環境では、以下のライブラリを使用しています

・Python本体 (動作確認時は3.9.5を使用)
・Matplotlibで表示可能な環境 (Jupyter等)
・下記ライブラリ (参考として動作確認時のライブラリバージョンも記載)
　lightgbm (3.2.1)
　scikit-learn (0.24.2)
　bayesian-optimization (1.2.0)
　optuna (2.7.0)
　numpy (1.20.3)
　pandas (1.2.4)
　seaborn (0.11.0)
　matplotlib (3.4.2)
・こちらの回帰可視化ライブラリ（チューニング前後のモデル可視化にのみ使用するので、なくともチューニング自体はできます）

使用するサンプルデータ

こちらの記事の、大阪都構想選挙データを使用します

ハードウェア

チューニング速度はCPU等の性能に大きく依存します
参考までに本記事で使用したPC（Lenovoのモバイル）のスペックを下記します

デバイス	スペック
CPU	Intel Core i5-8250U@1.6GHz
メモリ	8GB(4+4) DDR4 2400MHz SODIMM
ストレージ	SSD PCIe M.2
OS	Windows 10 Pro 64bit

コードの実行にはVSCodeのJupyter拡張を使用しております。

CPUやメモリの使用状況にもチューニングは左右されますが、余計なプロセスを終了してからチューニングを開始することで、繰り返してもほぼ同じ所要時間となり、再現性のとれる結果となりました。

実際の実装例

前述のフローに基づき実装を進めていきます

データの読込

こちらのデータセットをCSVからPandasのDataFrame（Jupyterでの表示用）およびNumpyのndarray（LightGBMモデルへの読込用）に読み込みます

データの読込

import pandas as pd
import time
df_osaka = pd.read_csv(f'./sample_data/osaka_metropolis_english.csv')
OBJECTIVE_VARIALBLE = 'approval_rate'  # 目的変数
USE_EXPLANATORY = ['2_between_30to60', '3_male_ratio', '5_household_member', 'latitude']  # 説明変数
y = df_osaka[OBJECTIVE_VARIALBLE].values  # 目的変数をndarray化
X = df_osaka[USE_EXPLANATORY].values  # 説明変数をndarray化
# データを表示
df_osaka[USE_EXPLANATORY + [OBJECTIVE_VARIALBLE]]

	2_between_30to60	3_male_ratio	5_household_member	latitude	approval_rate
0	0.499141	0.485807	1.83	42.325	0.562728
1	0.425080	0.481006	2.10	42.078	0.526104
2	0.467986	0.473394	2.06	41.535	0.536686
3	0.411267	0.473798	2.20	40.197	0.496048
4	0.390663	0.473722	2.16	43.273	0.471734
5	0.419868	0.474112	2.25	42.190	0.504592
6	0.422815	0.475847	2.52	42.257	0.511019
7	0.342897	0.577474	1.75	38.090	0.492851
8	0.506583	0.468446	1.65	40.870	0.509798
9	0.496780	0.467432	1.96	40.575	0.538094
10	0.374845	0.486567	2.34	39.018	0.465384
11	0.462086	0.505250	1.61	39.560	0.516693
12	0.383394	0.478802	2.36	36.575	0.486810
13	0.392461	0.465524	2.15	36.222	0.450049
14	0.390136	0.471774	2.38	37.270	0.456477
15	0.450164	0.464464	2.06	39.467	0.478386
16	0.368153	0.480087	2.27	39.218	0.480658
17	0.409648	0.460738	2.22	38.316	0.450814
18	0.386937	0.469701	2.23	37.322	0.473037
19	0.402482	0.488469	2.29	40.980	0.468385
20	0.400149	0.486460	2.18	39.835	0.429843
21	0.406196	0.490601	2.35	42.683	0.473805
22	0.433488	0.496974	1.97	43.260	0.550678
23	0.409827	0.491403	1.99	44.470	0.502997

チューニング前のモデルの確認

こちらのライブラリで、チューニング前モデルの特徴量と目的変数の関係を可視化します。

なお注意点として、ElasticNetの正則化は特徴量空間上での距離に基づいたアルゴリズムのため、前処理として標準化を行う必要があります。

Scikit-Learnにおいては、パイプラインを利用して標準化と回帰モデルを一体化すると便利です。
パイプラインに関しては以下の記事をご参照ください

線形回帰モデルの可視化

まずは、正則化を実施しない線形回帰での予測値を可視化します。

ElasticNetと条件を揃えるため、標準化とのパイプラインを構築します

チューニング前のモデル（線形回帰）

from seaborn_analyzer import regplot
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# 乱数シード
seed = 42
# モデル作成
model_linear = Pipeline([('scaler', StandardScaler()), ('lr', LinearRegression())])
# クロスバリデーションして予測値ヒートマップを可視化
cv = KFold(n_splits=3, shuffle=True, random_state=seed)  # KFoldでクロスバリデーション分割指定
regplot.regression_heat_plot(model_linear, USE_EXPLANATORY, OBJECTIVE_VARIALBLE, df_osaka,
                             pair_sigmarange = 0.5, rounddigit_x1=3, rounddigit_x2=3,
                             cv=cv, display_cv_indices=0)

男性比率(3_male_ratio)が高いほど、30-60代(2_between_30to60)が多いほど賛成率(approval_rate)が高い=色が濃いことが分かり、チューニング前でもある程度傾向が捉えられていることが分かります。

ちなみに、LinearRegressionはScikit-Learnにおける線形回帰を実行するクラス、StandardScalerが標準化を実行するクラス、KFoldがクロスバリデーションを実行するクラスです。

ElasticNetの可視化

デフォルトパラメータ（alpha=1, l1_ratio=0.5）でのElasticNet予測値を可視化します。

こちらも標準化とのパイプラインを構築します

チューニング前のモデル（ElasiticNet）

from seaborn_analyzer import regplot
from sklearn.linear_model import ElasticNet
from sklearn.model_selection import KFold
# 乱数シード
seed = 42
# モデル作成
model = ElasticNet()  # チューニング前のモデル
model = Pipeline([('scaler', StandardScaler()), ('enet', ElasticNet())])
# クロスバリデーションして決定境界を可視化
cv = KFold(n_splits=3, shuffle=True, random_state=seed)  # KFoldでクロスバリデーション分割指定
regplot.regression_heat_plot(model, USE_EXPLANATORY, OBJECTIVE_VARIALBLE, df_osaka,
                             pair_sigmarange = 0.5, rounddigit_x1=3, rounddigit_x2=3,
                             cv=cv, display_cv_indices=0)

全ての条件で同じ予測値（色の濃さ）となっており、うまく回帰できていないことが分かります。
チューニングでの改善が必要だと一目で分かります

ちなみに、ElasticNet()がScikit-LearnにおけるElasticNet回帰を実行するクラスです

手順1 最大化したい評価指標の定義

今回は
・回帰
・外れ値が多いデータではない
ので、こちらのフローに基づきRMSE（Scikit-Learnでは'neg_mean_squared_error')を採用します。

チューニング前の評価指標をクロスバリデーションで算出します。
モデルの挙動が分かりやすいよう、回帰式も同時に算出してみます。

線形回帰モデルの評価指標と回帰式

チューニング前の評価指標と回帰式算出（線形回帰）

from sklearn.model_selection import cross_val_score
import numpy as np
X = df_osaka[USE_EXPLANATORY].values  
y = df_osaka[OBJECTIVE_VARIALBLE]  # 目的変数をndarray化
scoring = 'neg_mean_squared_error'  # 評価指標をRMSEに指定
# クロスバリデーションで評価指標算出
scores = cross_val_score(model_linear, X, y, cv=cv,
                         scoring=scoring, n_jobs=-1)
print(f'scores={scores}')
print(f'average_score={np.mean(scores)}')
# 回帰式を表示
X_train, y_train = [(X[train], y[train]) for train, test in cv.split(X, y)][0]
trained_model = Pipeline([('scaler', StandardScaler()), ('lr', LinearRegression())])
trained_model.fit(X_train, y_train)
coef = trained_model['lr'].coef_
intercept = trained_model['lr'].intercept_
print(f'y = {coef[0]}*x1 + {coef[1]}*x2 + {coef[2]}*x3 + {coef[3]}*x4 + {intercept}')

scores=[-0.00055752 -0.00046975 -0.0011282 ]
average_score=-0.0007184895905236154
y = 0.024775155649700942*x1 + 0.02201069091006566*x2 + 0.003811059946280559*x3 + 0.006245497125570579*x4 + 0.486031836625

線形回帰でのスコア（neg_mean_squared_error = -MSE）は-0.000718
回帰式は
$$y = 0.0248x_1 + 0.0220x_2 + 0.0038x_3 + 0.0062x_4 + 0.4860$$
であることが分かりました。

ElasticNetの評価指標と回帰式

チューニング前の評価指標と回帰式算出（ElasticNet）

from sklearn.model_selection import cross_val_score
import numpy as np
X = df_osaka[USE_EXPLANATORY].values  
y = df_osaka[OBJECTIVE_VARIALBLE]  # 目的変数をndarray化
scoring = 'neg_mean_squared_error'  # 評価指標をRMSEに指定
# クロスバリデーションで評価指標算出
scores = cross_val_score(model, X, y, cv=cv,
                         scoring=scoring, n_jobs=-1)
print(f'scores={scores}')
print(f'average_score={np.mean(scores)}')
# 回帰式を表示
X_train, y_train = [(X[train], y[train]) for train, test in cv.split(X, y)][0]
trained_model = Pipeline([('scaler', StandardScaler()), ('enet', ElasticNet())])
trained_model.fit(X_train, y_train)
coef = trained_model['enet'].coef_
intercept = trained_model['enet'].intercept_
print(f'y = {coef[0]}*x1 + {coef[1]}*x2 + {coef[2]}*x3 + {coef[3]}*x4 + {intercept}')

scores=[-0.00164951 -0.00086281 -0.00165816]
average_score=-0.0013901602140001992
y = 0.0*x1 + 0.0*x2 + -0.0*x3 + 0.0*x4 + 0.486031836625

チューニング前のスコア（neg_mean_squared_error = -MSE）は-0.001390
回帰式は説明変数によらず0.486（全ての係数が0）
であることが分かりました。

前述の可視化の時点で予見はできましたが、線形回帰のときと比べるとかなり悪い指標となっています。
正則化（スパース性）が効きすぎて全ての説明変数の係数が0となってしまったと考えられます。

チューニングでこの値を改善していきます

手順2 パラメータ種類と範囲の選択

・種類

前述のように、alphaとl1_ratioの2つのパラメータを使用します。

注意点として、Scikit-Learnにおいてパイプラインを構成している場合、パラメータ名を
'[学習器名]__[パラメータ名]'
とする必要があります。

今回の場合、ElasticNetの学習器名を'enet'と指定しているので、パラメータ名は
enet__alpha
enet__l1_ratio
となります。

・範囲

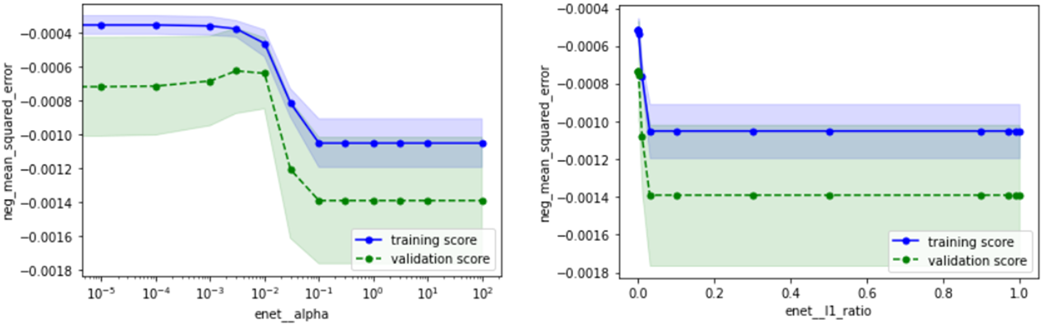
適当な初期範囲を定めて検証曲線をプロットし、その結果に基づいて範囲を調整していきます。

適当な初期範囲で検証曲線プロット

from sklearn.model_selection import validation_curve
import matplotlib.pyplot as plt
cv_params = {'enet__alpha': [0, 0.00001, 0.0001, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10, 100],
             'enet__l1_ratio': [0, 0.00001, 0.0001, 0.001, 0.01, 0.03, 0.1, 0.3, 0.5, 0.9, 0.97, 0.99, 1]
             }
param_scales = {'enet__alpha': 'log',
                'enet__l1_ratio': 'linear'
                }
# 検証曲線のプロット（パラメータ毎にプロット）
for i, (k, v) in enumerate(cv_params.items()):
    train_scores, valid_scores = validation_curve(estimator=model,
                                                  X=X, y=y,
                                                  param_name=k,
                                                  param_range=v,
                                                  cv=cv, scoring=scoring,
                                                  n_jobs=-1)
    # 学習データに対するスコアの平均±標準偏差を算出
    train_mean = np.mean(train_scores, axis=1)
    train_std  = np.std(train_scores, axis=1)
    train_center = train_mean
    train_high = train_mean + train_std
    train_low = train_mean - train_std
    # テストデータに対するスコアの平均±標準偏差を算出
    valid_mean = np.mean(valid_scores, axis=1)
    valid_std  = np.std(valid_scores, axis=1)
    valid_center = valid_mean
    valid_high = valid_mean + valid_std
    valid_low = valid_mean - valid_std
    # training_scoresをプロット
    plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
    plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
    # validation_scoresをプロット
    plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
    plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
    # スケールを'log'に（線形なパラメータは'linear'にするので注意）
    plt.xscale(param_scales[k])
    # 軸ラベルおよび凡例の指定
    plt.xlabel(k)  # パラメータ名を横軸ラベルに
    plt.ylabel(scoring)  # スコア名を縦軸ラベルに
    plt.legend(loc='lower right')  # 凡例
    # グラフを描画
    plt.show()

過学習または未学習になり過ぎない範囲を基準に、以下のようにチューニング範囲を定めます

※天下り的ですが、l1_ratioはalphaの値によってピーク位置が大きく変わるので、0～1全ての範囲をチューニング範囲に設定します。

手順3＆4 パラメータ選択＆クロスバリデーション

SVMのときと同様に、下記A、B、C (BayesianOptimization)、C (Optuna)の4種類の実装法をそれぞれ解説します。

	名称	概要	メリット	デメリット	ライブラリ
A	**グリッドサーチ　　　　　　**	パラメータを格子状に総当たり	シンプルで結果解釈性が高い	計算時間がかかる	Scikit-Learn
B	ランダムサーチ	パラメータをランダムに決定	平均的にはグリッドサーチより速い	運任せの要素あり	Scikit-Learn
C	ベイズ最適化	前回結果に基づきパラメータ決定	ランダムサーチより速い	ライブラリ操作がやや難	BayesianOptimization, Optuna

スコアと共にチューニングにかかった時間も測定し、各アルゴリズムで比較してみます。

処理時間は試行数にも依存するため、チューニング時間がほぼ等しくなるという基準で、各アルゴリズムの試行数を定めました

名称	試行数	early_stopping_roundなし時のチューニング所要時間
**グリッドサーチ　　　　　　**	182	2.6秒
ランダムサーチ	180	2.9秒
ベイズ最適化 (Bayesian Optimization)	35 (初期5+ベイズ30)	2.9秒
ベイズ最適化 (Optuna)	45	2.8秒

グリッドサーチの場合

GridSearchCVクラスで、グリッドサーチによる最適化を実行します。

下記のようにパラメータの組合せ（13x14=182通り）を設定し、グリッドサーチを実行します

グリッドサーチ＆クロスバリデーションの実装

from sklearn.model_selection import GridSearchCV
start = time.time()
# 最終的なパラメータ範囲(14x13通り)
cv_params = {'enet__alpha': [0.0001, 0.0002, 0.0005, 0.001, 0.002, 0.005, 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1],
             'enet__l1_ratio': [0, 0.00001, 0.00003, 0.0001, 0.0003, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 0.9, 0.97, 1]
             }
# グリッドサーチのインスタンス作成
gridcv = GridSearchCV(model, cv_params, cv=cv,
                      scoring=scoring, n_jobs=-1)
# グリッドサーチ実行（学習実行）
gridcv.fit(X, y)
# 最適パラメータの表示と保持
best_params = gridcv.best_params_
best_score = gridcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')

結果

最適パラメータ {'enet__alpha': 0.01, 'enet__l1_ratio': 0.3}
スコア -0.0005945065570814996
所要時間2.552086114883423秒

alpha=0.01
l1_ratio=0.3
のときに評価指標neg_mean_squared_errorが最大となり、その時の評価指標は-0.00594‥であることが分かります。

グリッドサーチで選択したパラメータと、算出した評価指標との関係をヒートマップで表示します。

探索点と評価指標を可視化

import seaborn as sns
import pandas as pd
# パラメータと評価指標をデータフレームに格納
param1_array = gridcv.cv_results_['param_enet__alpha'].data.astype(np.float64)  # パラメータgamma
param2_array = gridcv.cv_results_['param_enet__l1_ratio'].data.astype(np.float64)  # パラメータC
mean_scores = gridcv.cv_results_['mean_test_score']  # 評価指標
df_heat = pd.DataFrame(np.vstack([param1_array, param2_array, mean_scores]).T,
                       columns=['alpha', 'l1_ratio', 'test_score'])
# グリッドデータをピボット化
df_pivot = pd.pivot_table(data=df_heat, values='test_score', 
                          columns='alpha', index='l1_ratio', aggfunc=np.mean)
# 上下軸を反転（元々は上方向が小となっているため）
df_pivot = df_pivot.iloc[::-1]
# ヒートマップをプロット
hm = sns.heatmap(df_pivot, cmap='YlGn', cbar_kws={'label': 'score'})

この図から、以下のようなElasticNetの特徴が見て取れます。

前述のように、ElasticNetは線形回帰、Ridge回帰、Lasso回帰を内包していますが、
本ヒートマップにおいてはそれぞれ以下のような線上の位置関係となります。

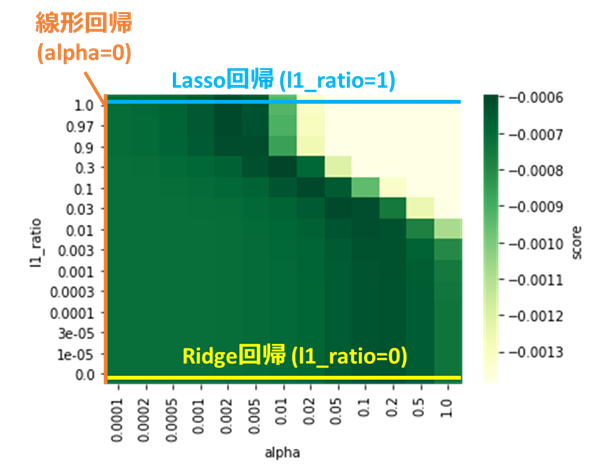
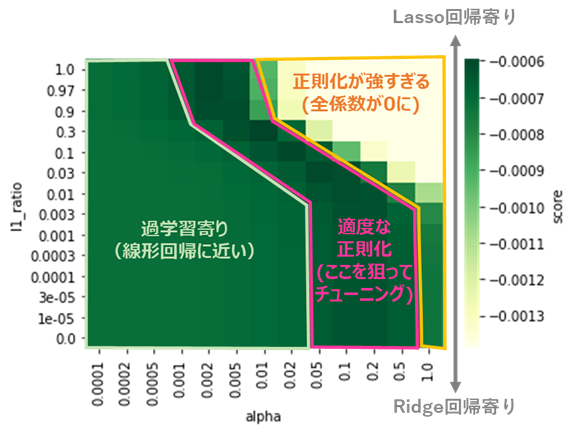
また、端部以外での挙動は、それぞれ以下のように分類できます。
ピンクの線で囲った部分において正則化が適度に機能しており、評価指標が高い=ヒートマップの緑色が濃くなっていることが分かります。
ElasticNetのパラメータチューニングは、この部分を狙ってパラメータを定める作業と解釈することができます。

ランダムサーチの場合

RondomizedSearchCVクラスで、ランダムサーチによる最適化を実行します

ランダムサーチ＆クロスバリデーションの実装

from sklearn.model_selection import RandomizedSearchCV
start = time.time()
# パラメータの密度をグリッドサーチのときより増やす
cv_params = {'enet__alpha': [0.0001, 0.0002, 0.0004, 0.0007, 0.001, 0.002, 0.004, 0.007, 0.01, 0.02, 0.04, 0.07, 0.1, 0.2, 0.4, 0.7, 1],
             'enet__l1_ratio': [0, 0.00001, 0.00002, 0.00005, 0.0001, 0.0002, 0.0005, 0.001, 0.002, 0.005, 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 0.9, 0.95, 0.99, 1]
             }
# ランダムサーチのインスタンス作成
randcv = RandomizedSearchCV(model, cv_params, cv=cv,
                            scoring=scoring, random_state=seed,
                            n_iter=180, n_jobs=-1)
# ランダムサーチ実行（学習実行）
randcv.fit(X, y)
# 最適パラメータの表示と保持
best_params = randcv.best_params_
best_score = randcv.best_score_
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')

結果

最適パラメータ {'enet__l1_ratio': 0.5, 'enet__alpha': 0.007}
スコア -0.0005963105732993489
所要時間2.892570734024048秒

alpha=0.007
l1_ratio=0.5
のときに評価指標neg_mean_squared_errorが最大となり、その時の評価指標は-0.00596‥であることが分かります。

ランダムサーチで選択したパラメータと、算出した評価指標との関係を散布図で表示します。

探索点と評価指標を可視化

# パラメータと評価指標をndarrayに格納
param1_array = randcv.cv_results_['param_enet__alpha'].data.astype(np.float64)  # パラメータgamma
param2_array = randcv.cv_results_['param_enet__l1_ratio'].data.astype(np.float64)  # パラメータC
mean_scores = randcv.cv_results_['mean_test_score']  # 評価指標
# 散布図プロット
sc = plt.scatter(param1_array, param2_array, c=mean_scores,
            cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc)  # カラーバー追加
cbar.set_label('score')  # カラーバーのタイトル
plt.xscale('log')  # 第1軸をlogスケールに
plt.yscale('linear')  # 第2軸をlinearスケールに
plt.xlim(np.amin(cv_params['enet__alpha']), np.amax(cv_params['enet__alpha']))  # X軸表示範囲をデータ最小値～最大値に
plt.ylim(np.amin(cv_params['enet__l1_ratio']), np.amax(cv_params['enet__l1_ratio']))  # Y軸表示範囲をデータ最小値～最大値に
plt.xlabel('alpha')  # X軸ラベル
plt.ylabel('l1_ratio')  # Y軸ラベル

ベイズ最適化（BayesianOptimization）の場合

BayesianOptimizationによるベイズ最適化の実装法を解説します。

なお、パラメータalphaはLogスケールのため、適宜スケールを変換しています

ベイズ最適化＆クロスバリデーションの実装(Logスケールに変数変換)

from bayes_opt import BayesianOptimization
start = time.time()
# パラメータ範囲（Tupleで範囲選択）
bayes_params = {'enet__alpha': (0.0001, 1),
                'enet__l1_ratio': (0, 1)
                }
# 対数スケールパラメータを対数化
param_scales = {'enet__alpha': 'log',
                'enet__l1_ratio': 'linear',
                }
bayes_params_log = {k: (np.log10(v[0]), np.log10(v[1])) if param_scales[k] == 'log' else v for k, v in bayes_params.items()}

# ベイズ最適化時の評価指標算出メソッド(引数が多いので**kwargsで一括読込)
def bayes_evaluate(**kwargs):
    params = kwargs
    # 対数スケールパラメータは10のべき乗をとる
    params = {k: np.power(10, v) if param_scales[k] == 'log' else v for k, v in params.items()}
    # モデルにパラメータ適用
    model.set_params(**params)
    # cross_val_scoreでクロスバリデーション
    scores = cross_val_score(model, X, y, cv=cv,
                             scoring=scoring, n_jobs=-1)
    val = scores.mean()
    return val

# ベイズ最適化を実行
bo = BayesianOptimization(bayes_evaluate, bayes_params_log, random_state=seed)
bo.maximize(init_points=5, n_iter=30, acq='ei')
# 最適パラメータとスコアを取得
best_params = bo.max['params']
best_score = bo.max['target']
# 対数スケールパラメータは10のべき乗をとる
best_params = {k: np.power(10, v) if param_scales[k] == 'log' else v for k, v in best_params.items()}
# 最適パラメータを表示
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')

※bo.maximizeの引数init_points, n_iter, acqは、こちらを参考に適宜変更してください

結果

最適パラメータ {'enet__alpha': 0.003207371536973375, 'enet__l1_ratio': 0.9883507719188748}
スコア -0.0005934357995616583
所要時間2.9344122409820557秒

alpha=0.0032‥
l1_ratio=0.998‥
のときに評価指標neg_mean_squared_errorが最大となり、その時の評価指標は-0.00593‥であることが分かります。

BayesianOptimizationで選択したパラメータと、算出した評価指標との関係を散布図で表示します。

探索点と評価指標を可視化

# パラメータと評価指標をDataFrameに格納
df_history = pd.DataFrame(bo.space.params, columns=bo.space.keys)  # パラメータ
df_history['enet__alpha'] = df_history['enet__alpha'].map(lambda x: np.power(10, x))  # alphaをLogスケールから戻す
mean_scores = bo.space.target  # 評価指標
# 散布図プロット
sc = plt.scatter(df_history['enet__alpha'].values, df_history['enet__l1_ratio'].values, c=mean_scores,
            cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc)  # カラーバー追加
cbar.set_label('score')  # カラーバーのタイトル
plt.xscale('log')  # 第1軸をlogスケールに
plt.yscale('linear')  # 第2軸をlinearスケールに
plt.xlim(bayes_params['enet__alpha'][0], bayes_params['enet__alpha'][1])  # X軸表示範囲をデータ最小値～最大値に
plt.ylim(bayes_params['enet__l1_ratio'][0], bayes_params['enet__l1_ratio'][1])  # Y軸表示範囲をデータ最小値～最大値に
plt.xlabel('alpha')  # X軸ラベル
plt.ylabel('l1_ratio')  # Y軸ラベル

ベイズ最適化（Optuna）の場合

Optunaによるベイズ最適化の実装法を解説します。

Optunaベイズ最適化＆クロスバリデーションの実装

import optuna
start = time.time()
# ベイズ最適化時の評価指標算出メソッド
def bayes_objective(trial):
    params = {
        'enet__alpha': trial.suggest_float('enet__alpha', 0.0001, 1, log=True),
        'enet__l1_ratio': trial.suggest_float('enet__l1_ratio', 0, 1)
    }
    # モデルにパラメータ適用
    model.set_params(**params)
    # cross_val_scoreでクロスバリデーション
    scores = cross_val_score(model, X, y, cv=cv,
                             scoring=scoring, n_jobs=-1)
    val = scores.mean()
    return val

# ベイズ最適化を実行
study = optuna.create_study(direction='maximize',
                            sampler=optuna.samplers.TPESampler(seed=seed))
study.optimize(bayes_objective, n_trials=40)

# 最適パラメータの表示と保持
best_params = study.best_trial.params
best_score = study.best_trial.value
print(f'最適パラメータ {best_params}\nスコア {best_score}')
print(f'所要時間{time.time() - start}秒')

結果

最適パラメータ {'enet__alpha': 0.003148911647956862, 'enet__l1_ratio': 0.9507143064099162}
スコア -0.000593780210887379
所要時間2.842801094055176秒

alpha=0.0031‥
l1_ratio=0.950‥
のときに評価指標neg_mean_squared_errorが最大となり、その時の評価指標は-0.00593‥であることが分かります。

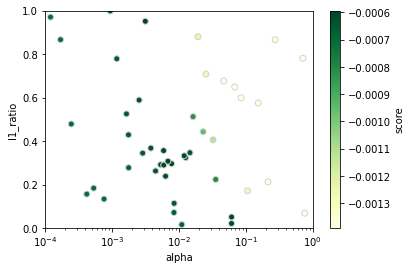
Optunaで選択したパラメータと、算出した評価指標との関係を散布図で表示します。

探索点と評価指標を可視化

# パラメータと評価指標をndarrayに格納
param1_array = [trial.params['enet__alpha'] for trial in study.trials]  # パラメータgamma
param2_array = [trial.params['enet__l1_ratio'] for trial in study.trials]  # パラメータC
mean_scores = [trial.value for trial in study.trials]  # 評価指標
# 散布図プロット
sc = plt.scatter(param1_array, param2_array, c=mean_scores,
            cmap='YlGn', edgecolors='lightgrey')
cbar = plt.colorbar(sc)  # カラーバー追加
cbar.set_label('score')  # カラーバーのタイトル
plt.xscale('log')  # 第1軸をlogスケールに
plt.yscale('linear')  # 第2軸をlinearスケールに
plt.xlim(0.0001, 1)  # X軸表示範囲をデータ最小値～最大値に
plt.ylim(0, 1)  # Y軸表示範囲をデータ最小値～最大値に
plt.xlabel('alpha')  # X軸ラベル
plt.ylabel('l1_ratio')  # Y軸ラベル

以上、4種類のアルゴリズムでのチューニング結果をまとめると、下の表のようになります。

名称	試行数	スコア(大きいほどGood)	所要時間
**グリッドサーチ　　　　　　**	182	-0.0005945	2.6秒
ランダムサーチ	180	-0.0005963	2.9秒
ベイズ最適化 (Bayesian Optimization)	35	-0.0005934	2.9秒
ベイズ最適化 (Optuna)	45	-0.0005938	2.8秒
所要時間を揃えたときの評価指標は、どの手法もほぼ同等です。

また、どの手法もこれ以上試行数を増やしてもあまり評価指標はよくなりません。
本データにおけるElasticNetの性能限界はneg_mean_squared_error=-0.00059（RMSE=0.024）前後にありそうです。
LightGBMやXGBoostではneg_mean_squared_errorが-0.00026くらいまで到達しているので、今回のデータセットにおける性能は、勾配ブースティングのような非線形な回帰手法が勝ることが分かります。

手順5 学習・検証曲線の確認

学習、検証曲線で過学習の有無を確認します。
今回はOptunaで調整したパラメータ（alpha=0.0031‥, l1_ratio=0.950‥）を例に描画してみます。

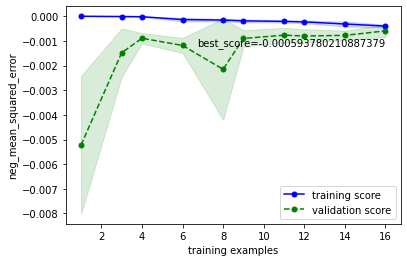
学習曲線

学習曲線をプロットし、
・目標性能を達成しているか
・過学習していないか
を確認します

学習曲線のプロット

from sklearn.model_selection import learning_curve
# 最適パラメータを学習器にセット
model.set_params(**best_params)

# 学習曲線の取得
train_sizes, train_scores, valid_scores = learning_curve(estimator=model,
                                                         X=X, y=y,
                                                         train_sizes=np.linspace(0.1, 1.0, 10),
                                                         cv=cv, scoring=scoring, n_jobs=-1)
# 学習データ指標の平均±標準偏差を計算
train_mean = np.mean(train_scores, axis=1)
train_std  = np.std(train_scores, axis=1)
train_center = train_mean
train_high = train_mean + train_std
train_low = train_mean - train_std
# 検証データ指標の平均±標準偏差を計算
valid_mean = np.mean(valid_scores, axis=1)
valid_std  = np.std(valid_scores, axis=1)
valid_center = valid_mean
valid_high = valid_mean + valid_std
valid_low = valid_mean - valid_std
# training_scoresをプロット
plt.plot(train_sizes, train_center, color='blue', marker='o', markersize=5, label='training score')
plt.fill_between(train_sizes, train_high, train_low, alpha=0.15, color='blue')
# validation_scoresをプロット
plt.plot(train_sizes, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
plt.fill_between(train_sizes, valid_high, valid_low, alpha=0.15, color='green')
# 最高スコアの表示
best_score = valid_center[len(valid_center) - 1]
plt.text(np.amax(train_sizes), valid_low[len(valid_low) - 1], f'best_score={best_score}',
                color='black', verticalalignment='top', horizontalalignment='right')
# 軸ラベルおよび凡例の指定
plt.xlabel('training examples')  # 学習サンプル数を横軸ラベルに
plt.ylabel(scoring)  # スコア名を縦軸ラベルに
plt.legend(loc='lower right')  # 凡例

こちらの確認方法に基づいて確認すると、下記のようにOKと判断できます
・目的の性能を達成しているか → 目標性能は定めていないが、チューニング前or線形回帰より向上（-0.001390 or -0.000718 → -0.000593）したのでOKとする
・過学習していないか → 検証データ指標と学習データ指標が収束しているのでOK

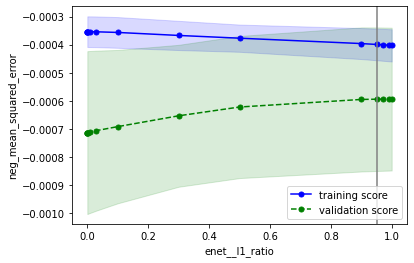
検証曲線

検証曲線をプロットし、
・性能の最大値を捉えられているか
・過学習していないか
を確認します

検証曲線のプロット

from sklearn.model_selection import validation_curve
# 検証曲線描画対象パラメータ
valid_curve_params = {'enet__alpha': [0, 0.00001, 0.0001, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 10, 100],
                      'enet__l1_ratio': [0, 0.00001, 0.0001, 0.001, 0.01, 0.03, 0.1, 0.3, 0.5, 0.9, 0.97, 0.99, 1]
                      }
param_scales = {'enet__alpha': 'log',
                'enet__l1_ratio': 'linear'
                }
# 最適パラメータを上記描画対象に追加
for k, v in valid_curve_params.items():
    if best_params[k] not in v:
        v.append(best_params[k])
        v.sort()
for i, (k, v) in enumerate(valid_curve_params.items()):
    # モデルに最適パラメータを適用
    model.set_params(**best_params)
    # 検証曲線を描画
    train_scores, valid_scores = validation_curve(estimator=model,
                                                  X=X, y=y,
                                                  param_name=k,
                                                  param_range=v,
                                                  cv=cv, scoring=scoring,
                                                  n_jobs=-1)
    # 学習データに対するスコアの平均±標準偏差を算出
    train_mean = np.mean(train_scores, axis=1)
    train_std  = np.std(train_scores, axis=1)
    train_center = train_mean
    train_high = train_mean + train_std
    train_low = train_mean - train_std
    # テストデータに対するスコアの平均±標準偏差を算出
    valid_mean = np.mean(valid_scores, axis=1)
    valid_std  = np.std(valid_scores, axis=1)
    valid_center = valid_mean
    valid_high = valid_mean + valid_std
    valid_low = valid_mean - valid_std
    # training_scoresをプロット
    plt.plot(v, train_center, color='blue', marker='o', markersize=5, label='training score')
    plt.fill_between(v, train_high, train_low, alpha=0.15, color='blue')
    # validation_scoresをプロット
    plt.plot(v, valid_center, color='green', linestyle='--', marker='o', markersize=5, label='validation score')
    plt.fill_between(v, valid_high, valid_low, alpha=0.15, color='green')
    # 最適パラメータを縦線表示
    plt.axvline(x=best_params[k], color='gray')
    # スケールをparam_scalesに合わせて変更
    plt.xscale(param_scales[k])
    # 軸ラベルおよび凡例の指定
    plt.xlabel(k)  # パラメータ名を横軸ラベルに
    plt.ylabel(scoring)  # スコア名を縦軸ラベルに
    plt.legend(loc='lower right')  # 凡例
    # グラフを描画
    plt.show()

こちらの確認方法に基づいて確認すると、下記のようにOKと判断できます
・性能の最大値を捉えられているか → どのパラメータもだいたい捉えられていそうなのでOKとする
・過学習していないか → データ数が少ないために多少の乖離はあるが、最適パラメータにおいて学習データ指標と検証データ指標が近づいているのでOK

チューニング後のモデルを可視化

最後に、チューニング後のモデルを可視化します（線形回帰と比較）

チューニング後のモデルと回帰式を可視化

regplot.regression_heat_plot(model, USE_EXPLANATORY, OBJECTIVE_VARIALBLE, df_osaka,
                             pair_sigmarange = 0.5, rounddigit_x1=3, rounddigit_x2=3,
                             cv=cv, display_cv_indices=0,
                             estimator_params=best_params)
# 回帰式を表示
X_train, y_train = [(X[train], y[train]) for train, test in cv.split(X, y)][0]
trained_model = Pipeline([('scaler', StandardScaler()), ('enet', ElasticNet())])
trained_model.set_params(**best_params)
trained_model.fit(X_train, y_train)
coef = trained_model['enet'].coef_
intercept = trained_model['enet'].intercept_
print(f'y = {coef[0]}*x1 + {coef[1]}*x2 + {coef[2]}*x3 + {coef[3]}*x4 + {intercept}')

y = 0.01544020933621683*x1 + 0.01099792887906393*x2 + -0.0*x3 + 0.005740875119903121*x4 + 0.486031836625

回帰式は
$$y = 0.0154x_1 + 0.0110x_2 + 0x_3 + 0.0057x_4 + 0.4860$$
であることが分かりました。

線形回帰と比べて色の濃淡=予測値の変化が小さくなっており、特に縦方向（3_male_ratio）の変化量が小さくなっています。
こちらの記事で触れた、正則化による選択的な回帰係数の低減が実現できていそうです。

また、3個目の変数（5_household_member）の係数は0となっており、Lasso回帰のようなスパース性を実現できている事もわかります。

想定通りの正則化による効果が見られ、評価指標も線形回帰より向上しているため、チューニング成功と言って良いのではと思います。

参考：線形回帰・Ridge回帰・Lasso回帰・ElasticNetのチューニング結果の比較

最後に、線形回帰＋正則化をベースとした回帰手法（線形回帰・Ridge回帰・Lasso回帰・ElasticNet）をOptunaでチューニングした結果を比較してみます。
データは上記と同じもの（大阪都構想データ）を使用します。

Ridge回帰とLasso回帰のチューニングおよび結果の可視化用コードは、以下のGitHubにアップロードしております。
Ridge回帰のパラメータチューニング
Lasso回帰のパラメータチューニング

手法	Optuna試行数	チューニング所要時間	スコア	変数1の係数	変数2の係数	変数3の係数	変数4の係数	切片
線形回帰	-	-	-0.000718	0.0248	0.0220	0.0038	0.0062	0.4860
Ridge回帰	45	1.9秒	-0.000636	0.0147	0.0103	-0.0025	0.0073	0.4860
Lasso回帰	45	1.9秒	-0.000593	0.0150	0.0106	0	0.0057	0.4860
ElasticNet	45	2.8秒	-0.000594	0.0154	0.0110	0	0.0057	0.4860

※変数1～4の内訳は以下となります
変数1：2_between_30to60
変数2：3_male_ratio
変数3：5_household_member
変数4：latitude

上記から、以下のような情報が読み取れます
・基本的には、線形回帰と比べて他手法は説明変数の係数が小さくなる（正則化の効果）
・本データにおいてはElasticNetとLasso回帰の係数が近い（l1_ratio=0.95と、L1正則化項が大きいため）
・ElasticNetやLasso回帰は、一部の係数が0となる（スパース性）
・どの手法も、切片はほぼ同じ（傾きのみが変わる）
・ElasticNetはLasso回帰やRidge回帰と比べやや処理時間が増える