この記事はなに?
この記事は連載している**ルービックキューブを解くロボットを作ろう!**という記事集の一部です。全貌はこちら
GitHubはこちら。
プロモーションビデオはこちらです。

この記事集に関する動画集はこちらです。

今回の記事の内容
今回は2x2x2ルービックキューブを解くための、(ロボットにとっての)最短手順を出力するプログラムのアルゴリズムについて解説します。アルゴリズムは「幅優先探索」と「IDA*」を紹介します。と、その前に全探索の考え方について軽く触れましょう。
今回考える「全探索」とは?
全探索は文字通り、全部のパターンを探索する手法です。2x2x2のルービックキューブであれば、ある状態から{U, U', U2, F, F', F2, R, R', R2}を回す場合すべてをチェックして、揃ってなければ前にチェックしたすべてのパターンに対してまた{U, U', U2, F, F', F2, R, R', R2}のすべてを回してチェックして…というような探索手法です(厳密には2手順目以降探索するのは各6手順ずつですが、その話はこのあとします)。ここで出てきたUとかFとかRは回転記号といいます。詳しくは概要編をご覧ください。
さて、ここでちょっと図を描いてみましょう。

このように、キューブの状態を丸(ノード)、その状態からなにか手を回すことを棒(辺)で表すと、ある状態から探索可能な手を全部回すことを繰り返していくこととこの木のような図が対応します。図ではサボりましたが、2x2x2の場合は各状態に対して、
- 最初の手は{U, U', U2, F, F', F2, R, R', R2}の9手
- 2手目以降は、前の手が{X, X', X2}のどれかだった場合は{U, U', U2, F, F', F2, R, R', R2}\{X, X', X2}の6手(\は差集合の記号)
これだけの手が回せるので、最初のノード(根)からは9本の辺が、最初以外のノードからはそれぞれ6本ずつ辺が生えていることになります。
なお、2手目以降に探索すべき手数が減るのは、例えばX X'と回したら何も回していないのと同じ、X Xと回せばX2、X X2と回せばX'と同じ、というように、2手同じ種類の回転記号が並ぶと相殺してしまうか別の回転記号一つに置き換わるかが必ず起きるためです。
幅優先探索
「幅優先探索」は「深さ優先探索」と並んで全探索の代表的な手法です。先程の図のノードに意図的に番号をつけたのはここでの説明のためにあります。ご察しの通り(?)深さ優先探索と幅優先探索では各ノードを調べる順番が違います。それぞれについて軽く説明しましょう。
幅優先探索
幅優先探索は図で言うと
1->1.1->1.2->1.3->...1.9->1.1.1->1.1.2->...1.1.6->1.2.1->1.2.2->...1.3.1->...1.1.1.1->...
と探索する探索方法です。なんのこっちゃ?と思いますので先程の図に矢印をつけましょう。

そうです、だんだん探索する深さが深くなっていく探索なのです。
図の番号で言うとだんだん探索するL.M.Nの数字が増えていきます。言い換えると、最初の状態からたくさん手を回すほど後の方に探索されます。
この探索手法は最短経路を見つけるときによく使います。というのも、「たくさん手を回すほど後の方に探索される」のであれば、「短い手数でなにかの解にたどりつくことがあればそれを見つけた時点で探索を打ち切れる」からです。
詳しく知りたい方はこちらの記事をおすすめします。
深さ優先探索
深さ優先探索の探索順序はこうです。
1->1.1->1.1.1->1.1.1.1->...1.2->1.2.1->1.2.1.1->...1.2.2->1.2.2.1->...
図も載せましょう。
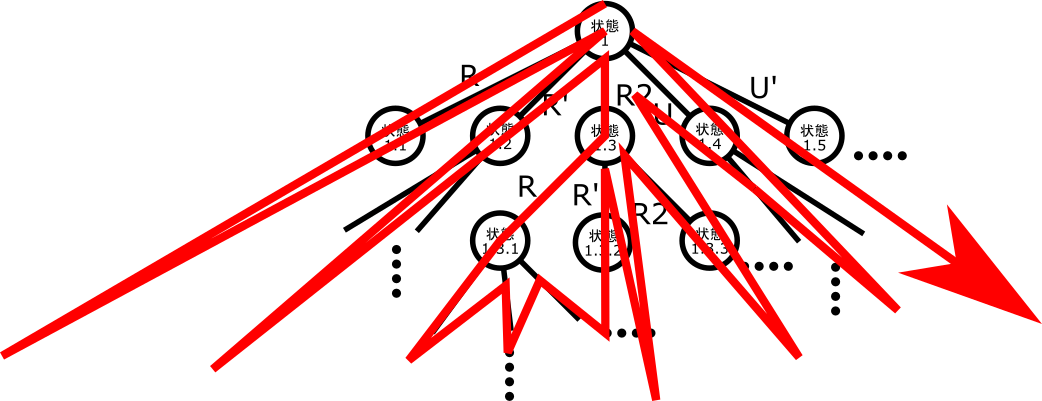
深さ優先探索は、とりあえず一番深い(手数の長い)ところまで探索して、だめだったら1つ浅いところに戻って(最後に回した手を別の手に替えてみる)…という探索手法です。
つまり、各深さについてL.M.Nなど、最後の数字がNのノードを調べる時には、すでにL.M.(N-1以下)のノードは調べ終わっていることになります。
この探索手法は実装が比較的簡単かつ(最適でない解(最短手順でない解)を探すのであれば)幅優先探索より高速に終わることがあり、メモリ使用量も比較的少ないため、とりあえず全探索をしたい場合によく使います。
幅優先探索でルービックキューブを解く
今回は最短手数を見つけたいので、幅優先探索を使います。とりあえず実装してみましょう。ここはPythonが読めない方はコメントだけ読んでふーんと聞き流してください。
from collections import deque
from copy import deepcopy
from time import time
move_candidate = ["U", "U2", "U'", "F", "F2", "F'", "R", "R2", "R'"] #回転の候補
# キューブのクラス 今回の記事では本質でない(ソフトウェア編で詳しく解説します)
class Cube:
def __init__(self):
self.Co = [0, 0, 0, 0, 0, 0, 0]
self.Cp = [0, 1, 2, 3, 4, 5, 6]
self.Moves = []
# 回転処理 CP
def move_cp(self, num):
surface = [[0, 1, 2, 3], [2, 3, 4, 5], [3, 1, 5, 6]]
replace = [[2, 0, 3, 1], [3, 2, 1, 0], [1, 3, 0, 2]]
idx = num // 3
res = Cube()
res.Cp = [i for i in self.Cp]
for i, j in zip(surface[idx], replace[num % 3]):
res.Cp[i] = self.Cp[surface[idx][j]]
res.Moves = [i for i in self.Moves]
res.Moves.append(num)
return res
# 回転処理 CO
def move_co(self, num):
surface = [[0, 1, 2, 3], [2, 3, 4, 5], [3, 1, 5, 6]]
replace = [[2, 0, 3, 1], [3, 2, 1, 0], [1, 3, 0, 2]]
pls = [2, 1, 1, 2]
idx = num // 3
res = Cube()
res.Co = [i for i in self.Co]
for i, j in zip(surface[idx], replace[num % 3]):
res.Co[i] = self.Co[surface[idx][j]]
if num // 3 != 0 and num % 3 != 1:
for i in range(4):
res.Co[surface[idx][i]] += pls[i]
res.Co[surface[idx][i]] %= 3
res.Moves = [i for i in self.Moves]
res.Moves.append(num)
return res
# 回転番号に則って実際にパズルの状態配列を変化させる
def move(self, num):
res = Cube()
res.Co = self.move_co(num).Co
res.Cp = self.move_cp(num).Cp
res.Moves = [i for i in self.Moves]
res.Moves.append(num)
return res
# 回転番号を回転記号に変換
def num2moves(self):
res = ''
for i in self.Moves:
res += move_candidate[i] + ' '
return res
# cp配列から固有の番号を作成
def cp2i(self):
res = 0
marked = set([])
for i in range(7):
res += fac[6 - i] * len(set(range(self.Cp[i])) - marked)
marked.add(self.Cp[i])
return res
# co配列から固有の番号を作成
def co2i(self):
res = 0
for i in self.Co:
res *= 3
res += i
return res
# パズルの状態 (R U R' U')3(この3はR U R' U'を3回回したという意味)を回した状態
# パズルがぐちゃぐちゃの状態からスタートして揃っている状態になるまで探索する
puzzle = Cube()
# CPはCorner Permutationの略。コーナーパーツの位置を表す。
puzzle.Cp = [1, 0, 2, 5, 4, 3, 6]
# COはCorner Orientationの略。コーナーパーツの向きを表す。
puzzle.Co = [2, 1, 0, 0, 0, 0, 0]
# 解けた状態でのパズルの状態
solved = Cube()
solved.Cp = [0, 1, 2, 3, 4, 5, 6]
solved.Co = [0, 0, 0, 0, 0, 0, 0]
# 時間計測
strt = time()
# 幅優先探索
que = deque([puzzle])
while que:
# キューから状態を取り出す
status = que.popleft()
# 最後に回した手順の番号をl_movに入れておく
l_mov = -1 if not status.Moves else status.Moves[-1]
# 次に回す手順のリスト
t = (l_mov // 3) * 3
lst = set(range(9)) - set([t, t + 1, t + 2])
for mov in lst:
# 実際にパズルを動かす
n_status = status.move(mov)
# 答えが見つかった!
if n_status.Cp == solved.Cp and n_status.Co == solved.Co:
print(n_status.num2moves())
print(time() - strt, '秒')
exit()
# 答えが見つからなかった場合、キューに状態を追加
que.append(n_status)
ちょっと長くなってしまいましたが、本題は最後の30行弱です。それ以外はキューブを表現するためのクラスだったりです。ソフトウェア編で詳しく話します。
このプログラムでは画像のスクランブル((R U R' U')3, 3はR U R' U'を3回やるという意味, R U R' U'がsexy moveと呼ばれることから、この動きは3sexyとも言う)を解いて、時間を計測しています。
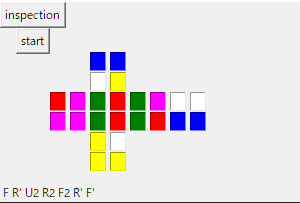
実行結果を見てみましょう。
F R F2 R2 U2 R F'
2.8320679664611816 秒
まず、解は3sexyじゃないんですねー(それはそうで、2x2x2キューブは最大でも11手で解けます)。そして、めちゃくちゃ時間がかかってしまっています。この原因を探るため、アマゾンの奥地へと向かうのではなく、計算量という概念を導入しましょう。
計算量
簡単に言えば、何回ループが回るか、という数字です。
$O(数字)$
という書き方をします。また、今回であれば解の長さ(=探索の深さ)が大事なので、それ以外の定数倍は無視します。
幅優先探索で回るループはwhile文ですね。これはqueに入れられた状態の個数分だけ回るので、計算量は
$O(\mathrm{que}に入れられた状態の個数)$
となります。計算してみましょう。
まず、最初のノードからは9本の辺が生えています。そして深さ2(2手目)以降では各ノードから辺が6本生えています。よって、深さを$N$とするとこのプログラムの計算量は、
$O(9\times 6^{N-1})$
です。
さて、今回のスクランブルは7手で解けたようです。$N=7$を代入してみましょう。
$O(9\times 6^6)=O(4.2\times10^5)$
今回は1つ1つの処理が重いのか、計算量がこれくらいでも遅くなってしまっています。
ちなみに2x2x2キューブは最大でも11手で揃う(神の数字)ので、$N=11$も代入してみましょう。
$O(9\times 6^{10})=O(5.4\times10^8)$
とんでもありません。これではほぼ永遠に終わってくれません!!
そこで高速化をするために登場するのが枝刈りです。
枝刈り
枝刈りとは、ある深さまで探索したときに、**このまま探索を進めても解にたどり着けない(キューブが揃わない)**とわかっている場合に探索をその時点で打ち切ることを言います。
今回はCO(Corner Orientation, コーナーパーツの向き)を無視してCP(Corner Permutation, コーナーパーツの位置)のみを揃える場合の最短手数、また、CPを無視してCOだけを揃える場合の最短手数の2つをあらかじめ計算しておき、CPかCOのどちらか一方でも11手(神の数字)以内に揃わないとわかった瞬間枝刈りをします。なんのこっちゃ、となると思いますので例として写真を載せましょう。左がCPのみが揃っている状態、右がCOのみが揃っている状態です。詳しくはソフトウェア編をご覧ください。

先程のプログラムの幅優先探索のところを以下のようにします。
inf = 100
fac = [1]
for i in range(1, 8):
fac.append(fac[-1] * i)
# 枝刈り用のCP配列を幅優先探索で作る
cp = [inf for _ in range(fac[7])]
cp_solved = Cube()
cp_solved.Cp = solved.Cp
cp[cp_solved.cp2i()] = 0
que = deque([cp_solved])
while len(que):
status = que.popleft()
num = len(status.Moves)
l_mov = status.Moves[-1] if num else -1
t = (l_mov // 3) * 3
lst = set(range(9)) - set([t, t + 1, t + 2])
for mov in lst:
n_status = status.move_cp(mov)
n_idx = n_status.cp2i()
if cp[n_idx] == inf:
cp[n_idx] = num + 1
que.append(n_status)
# 枝刈り用のCO配列を幅優先探索で作る
co = [inf for _ in range(3 ** 7)]
co_solved = Cube()
co_solved.Co = solved.Co
co[co_solved.co2i()] = 0
que = deque([co_solved])
while len(que):
status = que.popleft()
num = len(status.Moves)
l_mov = status.Moves[-1] if num else -1
t = (l_mov // 3) * 3
lst = set(range(9)) - set([t, t + 1, t + 2])
for mov in lst:
n_status = status.move_co(mov)
n_idx = n_status.co2i()
if co[n_idx] == inf:
co[n_idx] = num + 1
que.append(n_status)
print('前処理', time() - strt, 's')
# 幅優先探索
que = deque([puzzle])
while que:
# キューから状態を取り出す
status = que.popleft()
# 最後に回した手順の番号をl_movに入れておく
l_mov = status.Moves[-1] if len(status.Moves) else -1
# 次に回す手順のリスト
t = (l_mov // 3) * 3
lst = set(range(9)) - set([t, t + 1, t + 2])
for mov in lst:
# 実際にパズルを動かす
n_status = status.move(mov)
# 答えが見つかった!
if n_status.Cp == solved.Cp and n_status.Co == solved.Co:
print(n_status.num2moves())
print('全体', time() - strt, '秒')
exit()
elif len(n_status.Moves) + max(cp[n_status.cp2i()], co[n_status.co2i()]) < 11:
# 答えが見つからなかった場合、キューに状態を追加 ここのelifで枝刈りをしている
que.append(n_status)
この実行結果をみてみましょう。
前処理 0.433823823928833 s
F R F2 R2 U2 R F'
全体 2.1692698001861572 秒
お、少し速くなりましたね。でもまだちょっと遅いですね…1秒以内を目指したいところです。そしてメモリ使用量もそこそこあって厳しいものがあります。枝刈りをしたこのプログラムでもメモリ使用量は4.3GB程度あるようです。
そこでIDA*が登場します。
IDA*
IDAはIterative Deepening Aの略です。具体的な内容はこちらの記事に詳しく書かれていますので、私の記事では割愛しますが、この記事の中で個人的に一番わかりやすいと思った内容を抜粋して引用します。
IDAを一言で表すと、「最大深さを制限した深さ優先探索(DFS)を、深さを増やしながら繰り返す」です。
IDAのからくりは、一度探索したノードを忘れることにあります。ノードを忘れてしまえば、メモリを解放できますよね。
つまり、今回のルービックキューブを解くという内容であれば、深さ(手数)が1から11まで調べていき、その深さの範囲内で深さ優先探索をするということです。また、深さ$N-1$で最後まで探索して解が見つからなかった場合は探索したものをすべて忘れます。そして深さ$N$でまた探索し直すのです。一見非効率的ですが、これが意外とうまくいくのです。
深さ優先探索は必ずしも最適解を見つけるとは限らないと上でお話ししました。でもIDAでは、深さ$N$を調べるとき、深さ$N-1$までで解が存在しないことが保証されています。つまり、深さ$N$で解が見つかればそれが最適解なのです。また、深さ優先探索は比較的メモリ使用量が少ないともお話ししました。IDAではこの深さ優先探索を使うことで、メモリ使用量をぐっと減らします。
では実装してみましょう。先程のプログラムの枝刈りまでを拝借して、それ以降を書き換えます。
# IDA*
for depth in range(1, 12):
stack = [puzzle]
while stack:
# スタックから状態を取り出す。今回は深さ優先探索なのでpopleftではない
status = stack.pop()
# 最後に回した手順の番号をl_movに入れておく
l_mov = status.Moves[-1] if len(status.Moves) else -1
# 次に回す手順のリスト
t = (l_mov // 3) * 3
lst = set(range(9)) - set([t, t + 1, t + 2])
for mov in lst:
# 実際にパズルを動かす
n_status = status.move(mov)
# 答えが見つかった!
if len(n_status.Moves) == depth - 1 and n_status.Cp == solved.Cp and n_status.Co == solved.Co:
print(n_status.num2moves())
print('全体', time() - strt, '秒')
exit()
elif len(n_status.Moves) + max(cp[n_status.cp2i()], co[n_status.co2i()]) < depth:
# 答えが見つからなかった場合、スタックに状態を追加 ここのelifで枝刈りをしている
stack.append(n_status)
さっきと変わったのはdepthのfor文の追加とqueがstackになったことくらいです。なお、キューとスタックについてはこの記事では触れませんのでこちらの記事などを参照してください。
さて、結果やいかに。
前処理 0.352100133895874 s
F R' U2 R2 F2 R' F'
全体 0.36607813835144043 秒
爆速…!!
メモリ使用量はたったの93MBでした。最高ですねIDA*。
なお、深さ優先探索を再帰で書き、現在調べている回転番号(回転記号)の羅列を一つのスタックにして管理することでさらなるメモリ節約が期待できるという指摘を受けました。これについては実装が大幅に変わるほか、クラスを一部変更することが望ましくなるため、ここでは紹介しません。ソフトウェア編ではこの指摘を反映したプログラムを紹介します。
また、2x2x2ではなく3x3x3など分割数が多くなるとIDA*だけでは解法を見つけるのに時間がかかってしまうため、2フェーズアルゴリズムというものを使うのが一般的です。
まとめ
ここまで読んでくださりありがとうございます。ルービックキューブを解くアルゴリズムについて、なるべく平易に書いてみたつもりです(とは言っても私が今回このロボットを作ることで初めて知ったアルゴリズムであるIDA*なんてものはそう簡単には説明できない(し私も理解が浅い)のでかなり端折りましたが)。
これを機にアルゴリズムが好きな方、ルービックキューブを始めてみては?そしてルービックキューブが好きな方、アルゴリズムの勉強を始めてみては?