Go to Qiita Advent Calendar 2024 Top
LoginSignup
7
17

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@toyohisa

Pythonで0からディシジョンツリーを作って理解する　（1. 概要編）

Last updated at Posted at 2020-05-24

Pythonで0からディシジョンツリーを作って理解する
1.概要編 - 2. Pythonプログラム基礎編 - 3. データ分析ライブラリPandas編 - 4.データ構造編 - 5.情報エントロピー編 - 6.ツリー生成編 - (番外編) 離散化

AI（機械学習）やデータマイニングの学習のために、Pythonで0からディシジョンツリーを作成することによって理解していきます。

1.1 ディシジョンツリー（決定木）とは

1.1.1 ディシジョンツリーの例

例えば次のようなデータあるとします。天気、温度、湿度、風が次のようなときだったときに、ゴルフに行った日は〇、行かなかった日は×とします。このようなデータが14個あるとします。
データ例

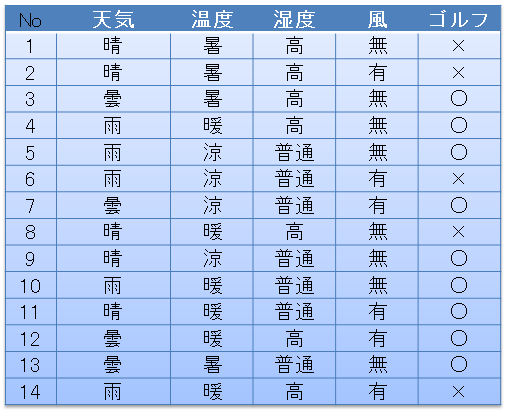
このデータから、ゴルフに行くときはどんなとき？というものを以下のようにツリー構造のルールとして記述したものを、ディシジョンツリー、または決定木と呼びます。
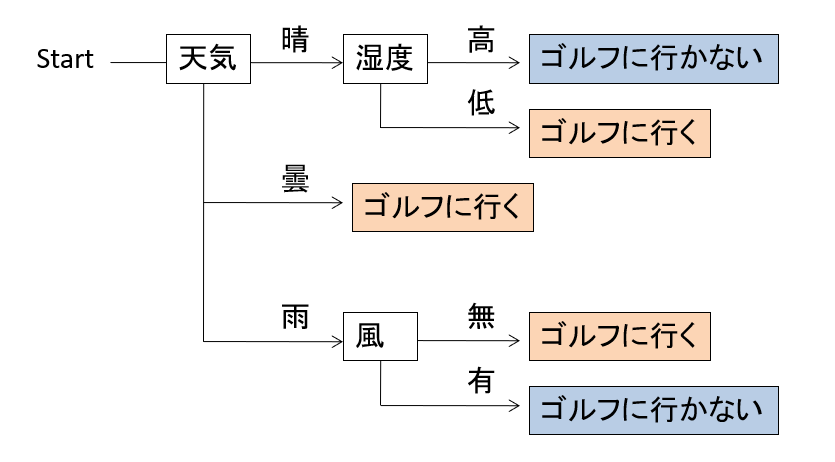
ディシジョンツリー例

例えばこのディシジョンツリーは、Startのところから見ていくと、まず天気について調べ、晴であれば次はその中で湿度について調べ、高い場合はゴルフに行く、低い場合にはいかない。また最初に戻って天気が曇りのときは、他の条件は関係なく、ゴルフに行く、とみることができます。

1.1.2 この記事について

このようなディシジョンツリーをデータから自動で作るアルゴリズムが知られています。この記事では、その中からID3というアルゴリズムについて、pythonを用いて実装します。

この1.概要編の以降は、次のように構成されています。

目的 記事
Pythonプログラムの基礎を学ぶ 2. Pythonプログラム基礎編
データ分析ライブラリのPandasについて必要なところだけを学ぶ 3. データ分析ライブラリPandas編
ディシジョンツリーというツリーをどのようにデータとしてプログラム内に持つかを学ぶ 4.データ構造編
ディシジョンツリーを作るための基礎となるデータの複雑さを表す情報エントロピーについて理解する 5.情報エントロピー編
ツリー構造を生成するアルゴリズムを学ぶ 6.ツリー生成編

1.1.3 ディシジョンツリー生成の学問上の位置づけ

ディシジョンツリーの生成は、主にAIの一部である機械学習における、教師付き学習の分類学習に属します。教師付き学習とは、正解情報のある学習用データから正解を導くモデルを自動的に作成する機械学習手法の総称で、分類学習とはデータを予め決められたクラスのどれに属するかを推測するものです。近年に流行している画像認識において好成績を収めているディープラーニング1も分類学習の一種です。ディープラーニングとディシジョンツリーの違いは、生成されるルールが人に理解できる形になっているか、否かです。答えは出すけどその理由が人間には分からない、といわれるディープラーニングと異なり、先のディシジョンツリーの例のようにルールが人にとって分かり易いということも、ディシジョンツリーの特徴です。
このルールが分かり易いという特徴を使って、単に答えをAIが出力すればよいという機械学習という分野だけでなく、データから知識を人間が発見するというデータマイニングという分野の一部としてもディシジョンツリーは見られています。

1.2 作成するアルゴリズム ID3について

ID32は、1986年にRoss Quinlanによって発明されたディシジョンツリー生成のアルゴリズムです。以下の特徴があります。

  1. カテゴリカルデータ（名義尺度）と呼ばれる、ゴルフに行く／行かないといったようなラベル化されたデータのみを扱います。数値データを取り扱うことは出来ません。
  2. 情報エントロピーという指標を用いて、クラス属性値（分類したい列）のバラツキが最も小さくなる属性（データの列のこと）を捜します。

1.2.1 数値データの扱いについて

ID3を発展させたC4.53というアルゴリズムの場合には、数値データの分類も可能となっていますが、基本的な考え方はID3と同じなのでID3をまずこの記事では取り上げます。。

1.3 開発環境

以下に示すプログラムは、次の環境で動作を確認しました。

  • Google Colaboratory
  • Python 3.10.12
  • import library: math, pandas(2.0.3), functools（scikit-learn, tensorflowなどは使いません）

1.4 プログラム例

1.4.1 プログラムの全文

とりあえずプログラムをColaboratoryにコピペすると、動作します。

id3.py
import math
import pandas as pd
from functools import reduce

# データセット
d = {
  "天気":["晴","晴","曇","雨","雨","雨","曇","晴","晴","雨","晴","曇","曇","雨"],
  "温度":["暑","暑","暑","暖","涼","涼","涼","暖","涼","暖","暖","暖","暑","暖"],
  "湿度":["高","高","高","高","普通","普通","普通","高","普通","普通","普通","高","普通","高"],
  "風":["無","有","無","無","無","有","有","無","無","無","有","有","無","有"],
  # 最後の列が、目的変数、正解データともよばれる、他の列から導き出したいデータとなる。
  "ゴルフ":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"],
}
dft = pd.DataFrame(d)

# 値の配分を求めるラムダ式、引数はpandas.Series、戻り値は各値の個数が入った配列
# 入力sからvalue_counts()で各値の度数を取得し、辞書型のデータのループ items()を呼び出す。
# sortedは、実行毎に出力結果が変化しないように、度数の小さい順に並べ替えている。
# そして、要素がキー(k)と値(v)の文字列となった配列を生成する。
cstr = lambda s:[k+":"+str(v) for k,v in sorted(s.value_counts().items())]

# ディシジョンツリーのデータ構造
tree = {
  # name: このノード(幹)の名前
  "name":"decision tree "+dft.columns[-1]+" "+str(cstr(dft.iloc[:,-1])),
  # df: このノードに関連付けられるデータ
  "df":dft,
  # edges: このノードから出ているエッジ(枝)一覧、下にエッジの無い葉ノードの場合は空配列となる。
  "edges":[],
}


# ツリーの生成は、枝が伸びる可能性のある幹についてこのopenに保存しておく。
open = [tree]

# エントロピーを計算するラムダ式、引数はpandas.Series、戻り値はエントロピーの数値
entropy = lambda s:-reduce(lambda x,y:x+y,map(lambda x:(x/len(s))*math.log2(x/len(s)),s.value_counts()))

# openが空になるまで繰り返す。
while(len(open)!=0):
  # openの先頭を取り出し、そのノードが保持しているデータを取り出しておく。
  n = open.pop(0)
  df_n = n["df"]

  # このノードのエントロピーが0の場合、これ以上エッジを展開できないので、
  # このノードからの枝分かれはしない。
  if 0==entropy(df_n.iloc[:,-1]):
    continue
  # 分岐可能性の属性値一覧を保存する変数を作成しておく。
  attrs = {}
  # クラス属性の最後の列以外の属性をすべて調査する。
  for attr in df_n.columns[:-1]:
    # この属性で分岐する場合のエントロピーと、
    # 分岐後のデータと分岐する属性値を保存する変数を作成する。
    attrs[attr] = {"entropy":0,"dfs":[],"values":[]}
    # この属性の取りうる値をすべて調査する。またsortedは、属性値の重複除去された配列を、
    # 実行のたびに順番が入れ替わらないようにするためである。
    for value in sorted(set(df_n[attr])):
      # 属性値でデータをフィルタリングする。
      df_m = df_n[df_n.loc[:,attr]==value]
      # エントロピーを計算し、関連するデータ、値をそれぞれ保存しておく。
      attrs[attr]["entropy"] += entropy(df_m.iloc[:,-1])*df_m.shape[0]/df_n.shape[0]
      attrs[attr]["dfs"] += [df_m]
      attrs[attr]["values"] += [value]
      pass
    pass
  # クラス値を分離可能な属性が1つも無い場合は、このノードの調査を終了する。
  if len(attrs)==0:
    continue
  # エントロピーが最小になる属性を取得する。
  attr = min(attrs,key=lambda x:attrs[x]["entropy"])
  # 分岐する属性のそれぞれの値、分岐後のデータを、ツリーとopenにそれぞれ追加する。
  for d,v in zip(attrs[attr]["dfs"],attrs[attr]["values"]):
    m = {"name":attr+"="+str(v),"edges":[],"df":d.drop(columns=attr)}
    n["edges"].append(m)
    open.append(m)
  pass

# データセットを出力する。
print(dft,"\n-------------")
# ツリーを文字に変換するメソッド、引数は tree:ツリーのデータ構造、indent:子ノードにつくインデント、
# 戻り値は、treeの文字表現。このメソッドは、再帰的に呼ばれて、ツリーのすべてを文字に変換する。
def tstr(tree,indent=""):
  # このノードの文字表現を作成する。このノードが葉ノードの場合(edges配列の要素数が0)には、
  # treeに関連付けられたデータdfの最後の列の度数分布を文字化する。
  s = indent+tree["name"]+str(cstr(tree["df"].iloc[:,-1]) if len(tree["edges"])==0 else "")+"\n"
  # このノードからのエッジについて、すべてループする。
  for e in tree["edges"]:
    # 子ノードの文字表現を、このノードの文字表現に付け加える。
    # indentには、このノードのindentに、さらに文字を加える。
    s += tstr(e,indent+"  ")
    pass
  return s
# ツリーを文字表現して、出力する。
print(tstr(tree))

1.4.2 実行結果

実行するとディシジョンツリーを文字表記として出力します。

decision tree ゴルフ ['×:5', '○:9']
  天気=晴
    湿度=普通['○:2']
    湿度=高['×:3']
  天気=曇['○:4']
  天気=雨
    風=有['×:2']
    風=無['○:3']

1.4.3 学習したい属性（データの列のこと）の変更

データ d の最後の列がクラス属性（分類したい目的のデータ列）となります。

data.py
d = {
    "天気":["晴","晴","曇","雨","雨","雨","曇","晴","晴","雨","晴","曇","曇","雨"],
    "温度":["暑","暑","暑","暖","涼","涼","涼","暖","涼","暖","暖","暖","暑","暖"],
    "湿度":["高","高","高","高","普通","普通","普通","高","普通","普通","普通","高","普通","高"],
    "ゴルフ":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"],
    # 最後の列が、目的変数、正解データともよばれる、他の列から導き出したいデータとなる。
    "風":["無","有","無","無","無","有","有","無","無","無","有","有","無","有"],
}

例えば、上記のように 風 を最後にして実行すると、次のような結果となります。

decision tree 風 ['有:6', '無:8']
  ゴルフ=×
    天気=晴
      温度=暑
        湿度=高['有:1', '無:1']
      温度=暖['無:1']
    天気=雨['有:2']
  ゴルフ=○
    天気=晴
      温度=暖['有:1']
      温度=涼['無:1']
    天気=曇
      温度=暑['無:2']
      温度=暖['有:1']
      温度=涼['有:1']
    天気=雨['無:3']

風が有る／無いのときは、ゴルフに行かない、行くでまず分岐し...っといったルールが作られます。

  1. Krizhevsky,A., Sutskerver,I and Hinton,G. E.: ImageNet classification with deep convolutional neural networks, NIPS 2012 (2012) ↩

  2. Quinlan, J. R.: Induction of Decision Trees. Mach. Learn. 1, 1, 81–106, (1986) ↩

  3. Quinlan, J. R.: C4.5: Programs for Machine Learning. Morgan Kaufmann Publishers, (1993). ↩

7
17
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
17

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?