Pythonで0からディシジョンツリーを作って理解する （5. 情報エントロピー編）

Pythonで0からディシジョンツリーを作って理解する
1.概要編 - 2. Pythonプログラム基礎編 - 3. データ分析ライブラリPandas編 - 4.データ構造編 - 5.情報エントロピー編 - 6.ツリー生成編 - (番外編) 離散化

AI（機械学習）やデータマイニングの学習のために、Pythonで0からディシジョンツリーを作成することによって理解していきます。

5.1 情報エントロピー（平均情報量）

ディシジョンツリーをデータから作るとき、どの属性で分岐すればもっとも効率的にデータを振り分けていけるかを、ID3アルゴリズムでは、情報エントロピーという指標によって決めています。

まず情報の量という概念を定義します。直感的には情報の量 = データの複雑さ、です。ディシジョンツリーは、ツリーの分岐を進むごとにデータは、同じクラス値のデータが集まり、つまりクラス値の複雑さは下がっていきます。よって、どの属性で分岐すれば良いのかを考えたとき、分割後のデータがどれだけシンプルになったのか、で判定すればよいとなります。

5.1.1 情報の量というものを定義する

情報量とは、取得した情報の価値のようなもので、起こる確率の低い事象について例えばそれが発生するといった情報は、よく起こる確率の高い事象について知ることよりも情報量が大きいとします。

例えば、2個の選択肢がある選択問題の答えを知ったときより、5個の選択肢の問題の答えを知ったときの方が、情報量が多いとなります。

そしてその事象を他者に伝えるために、2進数にエンコードして通信回線に流すとします。このときの通信量（ビット長）が情報量であると定義します。

事象Eが起こる確率をP(E)とするとき、事象Eが起こったということを知る情報量 I(E)は、次式のように定義されます。

I(E) = log_2(1/P(E)) = -log_2P(E)

5.1.2 情報エントロピー（平均情報量）とは

ある属性は、属性値を複数持っている。例えば天気属性は、晴、曇り、雨の3種類がある。そのそれぞれの生起確率から得る情報量の属性における平均値のことをエントロピー（平均情報量）といいます。

次の式のHで表されます。

H = -\sum_{E\in\Omega} P(E)\log_2{P(E)}

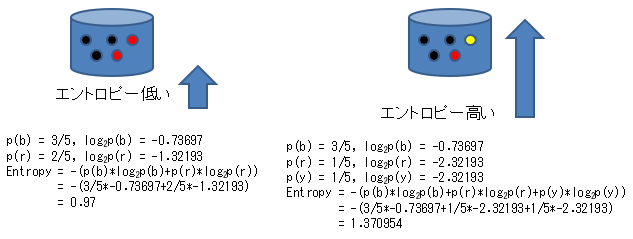
例えば次の図のような2つの属性におけるエントロピーは、次のように計算されます。より混じった、混沌とした左側はエントロピーが高く、左に比べて黒が支配的な右側の方がエントロピーが低いです。

しかし、複雑な式を使わなくても、上の例の場合、黒の数を見れば複雑さが求められる気もします。ただ、例えば黄色が追加された3値の場合を考えると、2値の場合でも3値でも同じように計算できる情報エントロピーの方が、統一性があって扱いやすいという面があります。

以下の例では、黒の数は同じであっても、残りが赤だけのものよりも、赤と黄色に分かれている方がエントロピーが高いと計算されます。

このID3というアルゴリズムは、よりエントロピーが低いグループにデータを分割する属性値を探す、というアルゴリズムです。

5.2 情報エントロピーの計算

情報エントロピーは、入力にDataFrame、出力をエントロピーの数値とした次のラムダ式で計算することができます。

entropy = lambda df:-reduce(lambda x,y:x+y,map(lambda x:(x/len(df))*math.log2(x/len(df)),df.iloc[:,-1].value_counts()))

これは、ラムダ式の中にさらにラムダ式が入っていますので、少し整理して次のように表示します。

entropy = lambda df:-reduce( #4.reduceは配列要素すべてから1つの値を作る。
    lambda x,y:x+y,#5.個々の値(9,5)から求められたエントロピーを足し合わせる。
    map( #2.度数配列(["○":9,"×":5])の数(9,5)を以下のlamda式でエントロピーに変換する
        lambda x:(x/len(df))*math.log2(x/len(df)),#3.P(E)log2(P(E))を計算する
        df.iloc[:,-1].value_counts() #1.DataFrameの最終列の度数（例:["○":9,"×":5]）
    )
)

この式は次の順番で処理されます。

1. df.iloc[:,-1]によってDataFrameの最終列が抽出され、value_countsによってその度数分布が得られます（度数分布の例：["○":9,"×":5]）。
2. mapによって度数分布の数値（例：9,5)のそれぞれがエントロピーの値に変換されます。
3. (x/len(df))*math.log2(x/len(df))によって、1つのエントロピーの式 $P(E)\log_2{P(E)}$ が計算されます。
4. reduceは、配列のすべての要素から1つの値を作るときに使用します。例えば、合計、平均などの計算に使用することができます。
5. lamda式 x,y : x+y によって2つの引数(x,y)の足し合わせた、つまり、配列の合計が求まります。これは、エントロピーの式 ($-\sum_{E\in\Omega} P(E)\log_2{P(E)}$)のシグマの部分になります。式の最初にマイナスが付いているので、プログラムのreduceの前にもマイナスが付いています。

5.2.1 計算例

次のようなデータの場合の情報エントロピーは、0.9402859586706309となります。

d = {"ゴルフ":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"]}
# エントロピーは、0.9402859586706309

一方、最初の2つの×が○に変わってより○が支配的なデータになった（複雑さが軽減された）場合のエントロピーは、0.74959525725948となります。

d = {"ゴルフ":["○","○","○","○","○","×","○","×","○","○","○","○","○","×"]}
# エントロピーは、0.74959525725948

情報エントロピーを計算するすべてのプログラムを以下に示します。

import pandas as pd
from functools import reduce
import math

d = {"ゴルフ":["×","×","○","○","○","×","○","×","○","○","○","○","○","×"]}
df0 = pd.DataFrame(d)

entropy = lambda df:-reduce(
    lambda x,y:x+y,
    map(
        lambda x:(x/len(df))*math.log2(x/len(df)),
        df.iloc[:,-1].value_counts()
    )
)

print(entropy(df0)) # 出力 0.9402859586706311