Pythonで0からディシジョンツリーを作って理解する （4. データ構造編）

Pythonで0からディシジョンツリーを作って理解する
1.概要編 - 2. Pythonプログラム基礎編 - 3. データ分析ライブラリPandas編 - 4.データ構造編 - 5.情報エントロピー編 - 6.ツリー生成編 - (番外編) 離散化

AI（機械学習）やデータマイニングの学習のために、Pythonで0からディシジョンツリーを作成することによって理解していきます。

4.1 データ構造

データ構造とは、個々のデータがどうやって並んでいるのかを表したものです。

配列、一次元配列

個々のデータが一列に並んでいます。1つのデータを特定するには、例えば何番目のデータのように、1つの識別子が必要になります。

# 配列のpythonでの実装例
a = [2,6,4,5,1,8]

# データが文字の場合、" (ダブルクオーテーション)か、' (シングルクォーテーション)で文字を囲む
a = ["太郎","次郎"]

二次元配列、テーブル

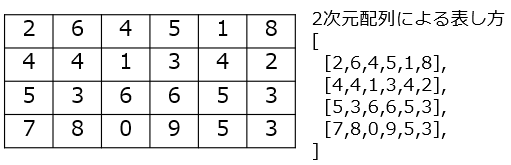
データの列が複数あり、平面上に個々のデータが並んでいます。1つのデータを特定するには、何列目の何番目かのように、2つの識別子が必要になります。

# テーブルのpythonでの実装例
a = [
    [2,6,4,5,1,8],
    [4,4,1,3,4,2],
    [5,3,6,6,5,3],
    [7,8,0,9,5,3],
]

ツリー、木構造

個々のデータを線で結んだようなデータ構造です。但し、線は巡回せず、例えばあるデータからある別のデータへの経路を考えるときに、その経路が1本のものがツリー構造のデータです。上図のように、よく上から下に伸びる木のように図示されることがあります。線のことをエッジ、枝などと呼び、データのことをノード、さらに下に線が続くデータを幹や節点、線が続かないデータを葉やリーフ、一番上のデータをルートノードや根と呼んだりします。線には矢印が付いて一方通行になっていることもあります。

Pythonのデータとして表す場合、様々な方法が考えられるわけですがここでは [名前, [子ノード1,子ノード2,...]]という形式で1つのノードを表す方法を示します。上図のツリーは、その右のようなリストが1つになったもので表すことができます。より具体的には以下のコードのようになります。

# ツリーのpythonでの実装例 子ノード一覧を保持する。
# [値,子ノード一覧の配列]として、例えば上のツリーを、上から下、左から右に実装と次のようになる。
# この実装方法以外にも、クラスを使う、親ノードを保持する、などがある。
tree = \
[2,[
    [6,[]],
    [4,[
        [5,[
            [6,[]],
        ]],
        [8,[]],
        [1,[]],
    ]],
]]

# ツリー構造の文字化関数
def tstr(node,indent=""):
    s = indent+str(node[0])+"\n"
    for c in node[1]: # 子ノードでループ
        s += tstr(c,indent+"+-")
        pass
    return s
print(tstr(tree))
# 出力
# 2
# +-6
# +-4
# +-+-5
# +-+-+-6
# +-+-8
# +-+-1

# 一度にツリー全体を作らずに、1つずつ作る場合
# 子ノードが無い葉ノードをすべて作成する。変数名は、行（段）、左からの数を付けるとする。
# 一番下の 6 のノード
n0_0 = [6,[]]
# 下から2段目の5,8,1のノード
n1_0 = [5,[n0_0]]
n1_1 = [8,[]]
n1_2 = [1,[]]
# 下から3段目の6,4のノード
n2_0 = [6,[]]
n2_1 = [4,[n1_0,n1_1,n1_2]]
# 下から4段目（最上位）の 2 のノード
n3_0 = [2, [n2_0,n2_1]]

# ツリー構造の表示、指定したノードをルートノードとして表示する。
print(tstr(n3_0))
# 出力
# 2
# +-6
# +-4
# +-+-5
# +-+-+-6
# +-+-8
# +-+-1

ネットワーク、グラフ

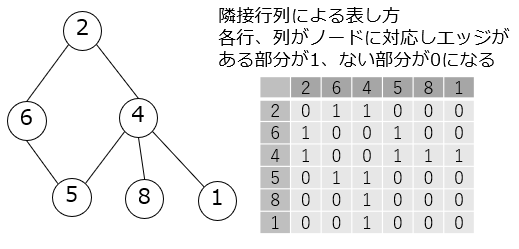
巡回する線があるデータを線で結んだデータ構造のことです。ツリー構造と同じように、線に矢印が付いて一方通行になることもあります。個々のデータをノード、線をエッジと呼びます。木構造のようにデータのスタート地点が無い場合が多いので、ルート、幹、葉などの呼び方はあまりしません。

# ネットワークのpythonでの実装例
import pandas as pd

# ノードの名称と、値が一致しているとする。
# 名称と値が一致していない場合には、名前から値を引くデータが必要になる。
nodes = [2,6,4,5,8,1]
# 行列の形式でノードの接続状況を定義する。ノード2(1行目)から、ノード6(2行目)へエッジがある場合には、
# 行列の1行2列の値が1、エッジが無い場合は0になる。この行列を、隣接行列という。
df = pd.DataFrame(
[
    # 2,6,4,5,8,1 のノードに接続があるか？
    [ 0,1,1,0,0,0], # 2のノードから
    [ 1,0,0,1,0,0], # 6のノードから
    [ 1,0,0,1,1,1], # 4のノードから
    [ 0,1,1,0,0,0], # 5のノードから
    [ 0,0,1,0,0,0], # 8のノードから
    [ 0,0,1,0,0,0], # 1のノードから
],columns=nodes,index=nodes)
print(df)
# 出力
#    2  6  4  5  8  1
# 2  0  1  1  0  0  0
# 6  1  0  0  1  0  0
# 4  1  0  0  1  1  1
# 5  0  1  1  0  0  0
# 8  0  0  1  0  0  0
# 1  0  0  1  0  0  0

# matplotlibと、networkxというライブラリによって、ネットワークを描画する。
import matplotlib.pyplot as plt
import networkx as nx
plt.figure(figsize=(4,4))
plt.axis("off")
nx.draw_networkx(nx.from_pandas_adjacency(df))
plt.show()

ネットワークの出力例

4.2 ディシジョンツリーのpythonによる実装例

ディシジョンツリーは、その名の通り、ツリー構造によって表すことができます。ノードが保持するデータとしては、ツリー構造をもつための子ノード一覧以外には、分岐するためのルール、および、ディシジョンツリーの中でこのノードまでたどり着くデータ一覧となります。

以下のように、ルートノードには空のノードを置き、全データを関連付けます。ノードに付けられた[...]の数値は、このディシジョンツリーが作られる元データのデータ番号を表しています。そしてルートノードから、子ノードの条件に充たすデータだけが、ツリーを降りていくように表現することができます。ディシジョンツリーにある、ゴルフに行く、ゴルフに行かないというノードは、ノードに関連付けられたデータを見れば分かります。

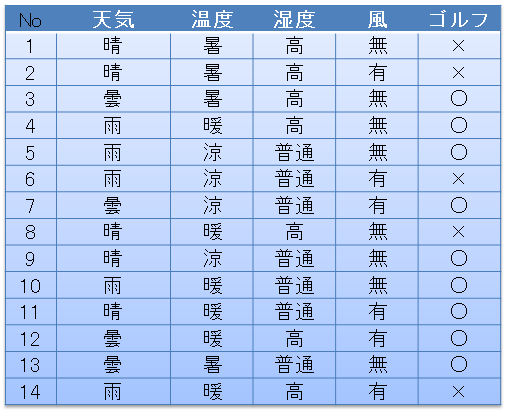
pythonによる実装は、例えば次のようです。1つのノードを連想配列とし、nameにはそのノードの条件を文字表現したもの、dfにはそのノードに関連付けられたデータ、そしてedgesには子ノード一覧を持ちます。

# 木構造のデータ
tree = {
    # name: このノード(幹)の名前
    "name":"decision tree "+df0.columns[-1]+" "+str(cstr(df0.iloc[:,-1])),
    # df: このノードに関連付けられるデータ
    "df":df0,
    # edges: このノードから出ているエッジ(枝)一覧、下にエッジの無い葉ノードの場合は空配列となる。
    "edges":[],
}

この木構造を文字化する関数 tstr は、次のようになります。

# 値の配分を求めるラムダ式、引数はpandas.Series、戻り値は各値の個数が入った配列
# 入力sからvalue_counts()で各値の度数を取得し、辞書型のデータのループ items()を呼び出す。
# sortedは、実行毎に出力結果が変化しないように、度数の小さい順に並べ替えている。
# そして、要素がキー(k)と値(v)の文字列となった配列を生成する。
cstr = lambda s:[k+":"+str(v) for k,v in sorted(s.value_counts().items())]

# ツリーを文字に変換するメソッド、引数は tree:ツリーのデータ構造、indent:子ノードにつくインデント、
# 戻り値は、treeの文字表現。このメソッドは、再帰的に呼ばれて、ツリーのすべてを文字に変換する。
def tstr(tree,indent=""):
    # このノードの文字表現を作成する。このノードが葉ノードの場合(edges配列の要素数が0)には、
    # treeに関連付けられたデータdfの最後の列の度数分布を文字化する。
    s = indent+tree["name"]+str(cstr(tree["df"].iloc[:,-1]) if len(tree["edges"])==0 else "")+"\n"
    # このノードからのエッジについて、すべてループする。
    for e in tree["edges"]:
        # 子ノードの文字表現を、このノードの文字表現に付け加える。
        # indentには、このノードのindentに、さらに文字を加える。
        s += tstr(e,indent+"  ")
        pass
    return s

このtstr関数によって文字化されたディシジョンツリーは、次のようになります。ルートノードは、最初にtree変数を作成したときにセットした文字(decision tree ゴルフ)と全データのゴルフに行く／行かないの度数分布が表示されています。その下の各ノードでは、分岐に使用されるルールと、葉ノードの場合には、そのノードに関連付けられたデータのゴルフに行く／行かないの度数分布(例えば、['○:2'])が表示されています。

decision tree ゴルフ ['×:5', '○:9']
  天気=晴
    湿度=普通['○:2']
    湿度=高['×:3']
  天気=曇['○:4']
  天気=雨
    風=有['×:2']
    風=無['○:3']