Pythonで0からディシジョンツリーを作って理解する
1.概要編 - 2. Pythonプログラム基礎編 - 3. データ分析ライブラリPandas編 - 4.データ構造編 - 5.情報エントロピー編 - 6.ツリー生成編 - (番外編) 離散化
AI(機械学習)やデータマイニングの学習のために、Pythonで0からディシジョンツリーを作成することによって理解していきます。
6.1 ツリー生成のアルゴリズム
6.1.1 ツリー生成のアルゴリズムとは
ツリー構造を、例えば親子関係のデータをつなぎ合わせて作り出すアルゴリズムのことをツリー生成のアルゴリズムとここでは呼んでいます。
6.1.2 親ノードから子ノードを捜してつなぐ
ツリーのデータ構造としては、親ノードが子ノード一覧を保持する方法と、子ノードが親を保持する方法の2種類が考えられます。ただ、ツリー構造のデータを生成する方法としては、基本的には、親から子を捜すことになります。その理由は、ツリー構造は、親から複数の子ノードがあるため、子から親に遡るだけだとツリー構造に含まれない子ノードが現れてしまうからです。ただもちろん、親ノードから子ノードを捜す過程の中で、作成するツリー構造は、子ノードが親ノードを記録するという構造にすることは出来ます。
6.1.3 アルゴリズムの例
ツリー構造の元になる、あるデータがありそこから子ノード一覧を取得し続けるアルゴリズムです。
- ツリーの最上部の根になるデータを、これから調査対象となるopen配列に入れる。
- open配列が空になるまで3~5を繰り返す。
- openの先頭を取り出す。これをnとする。
- nの子ノード一覧を調査し、それらをmとする。
- mを、nの子ノード一覧とopen配列にそれぞれ追加する。
「4. nの子ノード一覧を調査し、それらをmとする。」の調査の部分を具体化することによって、以下に示す家系図の作成や、本記事の主テーマであるディシジョンツリーの作成に使用することができます。
例えば次のような親子関係を表すリストデータがあるとします。parent_childsリストは[親,子]といったリストを複数保持するリストとなっています。
parent_childs = [
[2,6],
[2,4],
[4,5],
[4,8],
[4,1],
[5,6],
]
ノード2をルートとしたツリーを作成する場合、openに2、完成させたいツリーを表すtree変数に[2,[]]という2をルートとし子がまだないツリー構造をセットします。そして上記のアルゴリズムを実行すると次のように、open、tree変数は変わっていきます。
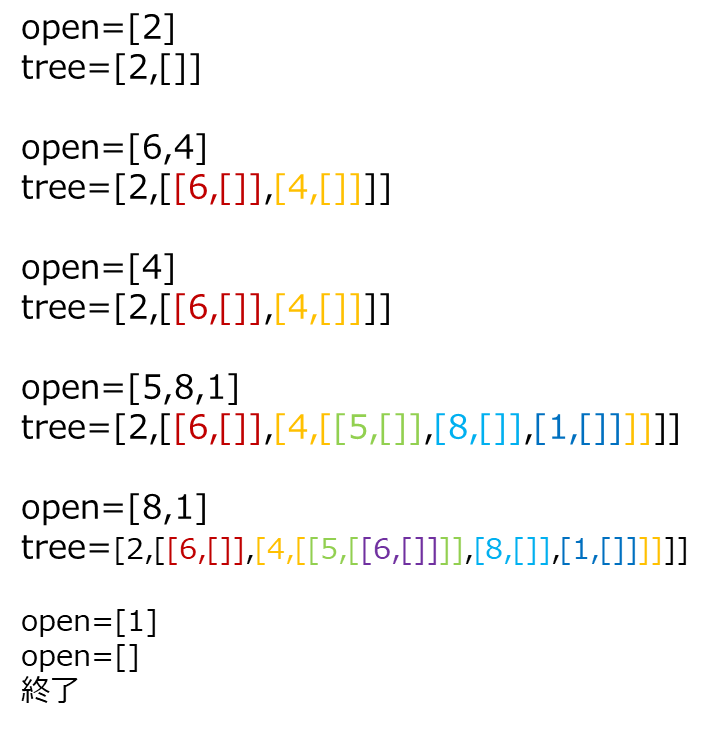
アルゴリズムは、open変数が空になったところで終了し、その時のtree変数にはノード2をルートとしたツリー構造が完成されています。ちなみにそのツリーは、以下のようです。
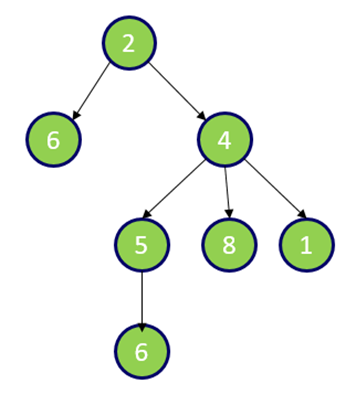
6.1.4 ツリー生成の2つの戦略、幅優先(横型)、深さ優先(縦型)
ツリー生成には次の2つの戦略があります。
- 幅優先(横型)探索: ツリーが全体的に伸びていきます。
- 深さ優先(縦型)探索: 1本の枝が伸びきったら次の枝が伸び始めます。
この2つは、6.1.2 アルゴリズムで紹介した「5. nの子ノード一覧と、open配列にそれぞれmを追加する。」のopenへの追加の仕方によって変えることができます。
新しく発見された子ノードmをopenの最後尾に追加すると幅優先、先頭に追加すると深さ優先になります。なぜならopenは、次に調査するノードを先頭から取り出すので、新しいノードmをopenの最後尾に追加すれば先にopenに入っているノードが優先され、またopenの先頭に追加されればそのmが最優先で次の調査に選ばれることになるからです。
結果的に次のように、幅優先の場合には、ツリー最上位のノードから1段ずつ下に下がるようにノードがツリーに追加されていきます。0,1,2などの番号は、ツリーに追加される順番を表しています。そして深さ優先の場合には、最初に追加されたノード(図では1番のノード)の下を先にツリーに追加し、1のノードの子ノードがすべてなくなってから、1の隣の5ノード、そして6ノードと追加されていきます。

どちらの戦略が良いかは、一概には言えません。ただ実装の仕方として、6.1.2のアルゴリズムは、どちらでも対応できますが、深さ優先の場合には6.1.2のアルゴリズムではなく、再帰関数を用いた実装もできます。その実装のし易さから深さ優先が選ばれることもあります。
ただこの2つの戦略の違いは、例えば膨大な大きさのツリーを作るとき、コンピュータのメモリ容量や処理時間を考慮してツリーの一部分だけを作りたいようなとき以外は、あまり大きく影響しません。どちらの戦略でも同じツリーが作成されるからです。
6.2 徳川将軍家の家系図のツリー構造化
次のような徳川将軍家の家系図を、ツリー構造としてデータ化する例を示します。

(参照: wikipedia)
6.2.1 親子関係のデータからツリーを作る
ツリー構造を作るための元データは、次のような、["親","子"]といった親子関係を配列のセットとします。
# 親子関係を配列で表したデータ
parent_childs = [
["家康","信康"],["家康","秀康"],["家康","秀忠"],["家康","忠輝"],["家康","義直"],
["秀忠","家光"],["秀忠","忠長"],["秀忠","和子"],["秀忠","正之"],["家光","家綱"],
["家光","綱重"],["家光","綱吉"],["綱重","家宣"],["家宣","家継"],["家康","頼信"],
["頼信","光貞"],["光貞","吉宗"],["吉宗","家重"],["家重","家治"],["家重","重好"],
["吉宗","宗武"],["宗武","定信"],["吉宗","宗尹"],["宗尹","治済"],["治済","家斉"],
["治済","斉敦"],["治済","斉匡"],["家斉","家慶"],["家慶","家定"],["家斉","斉順"],
["斉順","家茂"],["斉匡","慶頼"],["慶頼","家達"],["家康","頼房"],["頼房","頼重"],
["頼重","頼侯"],["頼侯","頼豊"],["頼豊","宗堯"],["宗堯","宗翰"],["宗翰","治保"],
["治保","治紀"],["治紀","斉昭"],["斉昭","慶喜"],
]
6.2.2 ツリー生成アルゴリズムの実装例
根元になるノードを指定して、そこから下の子ノードをすべてツリー構造データ化する関数を示します。関数の引数には、親ノードと、親子関係のデータを指定します。戻り値は、生成されたツリー構造です。また、引数として指定した親ノードに追加する形でツリー構造を作成するので、引数の親ノードの値は改変されます。
# 祖を指定して、ツリー構造を作成する。
def tree_generator(tree,rdata):
# こから調査する対象のノード一覧
open = [tree]
# openが空になるまで繰り返す。
while(len(open)!=0):
# open の先頭を取り出す。
n = open.pop(0)
# 親子関係のデータをすべてループする。
for pc in rdata:
# 親データと調査対象データが一致する場合
if pc[0]==n[0]:
# ツリーデータを作成して、調査対象のツリーの子ノードとして追加する。
m = [pc[1],[]]
n[1].append(m)
# さらに発見された子ノードを、これから調査をする対象としてopenに登録する。
open.append(m)
pass
pass
pass
return tree
6.2.3 ツリーの表示
4.データ構造編で示した。ツリー構造を文字化する関数です。
# ツリー構造の表示関数
def tstr(node,indent=""):
s = indent+str(node[0])+"\n"
for c in node[1]: # 子ノードでループ
s += tstr(c,indent+"+-")
pass
return s
6.2.4 ついでに何代の将軍かを表示
ツリー構造とは関係が無いのですけど、せっかくなので、徳川宗家の誰が何代将軍なのかを名前の横に数値を記すことによって表したいと思います。
まず、将軍配列(shogun)を作成し、そのインデックス+1が何代かを表すので、それを取得するラムダ式を作っておきます。将軍ではない名前が指定されると空欄が返されます。
これを、先ほどのツリー構造の文字化関数(tstr)の文字生成部分に追加します。
# 歴代将軍の配列
shogun = ["家康","秀忠","家光","家綱","綱吉","家宣","家継",
"吉宗","家重","家治","家斉","家慶","家定","家茂","慶喜"]
# 名前から何代将軍かを求める。将軍ではない場合は、空文字が返る。
sno = lambda name: "" if name not in shogun else " "+str(shogun.index(name)+1)
# tstr関数の文字生成部分に、sno(node[0])を追加する。
s = indent+str(node[0])+sno(node[0])+"\n"
6.2.5 実行例
家康を祖とした全家系図を表示する場合です。
# 家康を祖とした家系図を作成する。
tree = ["家康",[]]
tree_generator(tree,parent_childs)
print(tstr(tree))
#出力
#家康 1
#+-信康
#+-秀康
#+-秀忠 2
#+-+-家光 3
#+-+-+-家綱 4
#+-+-+-綱重
#+-+-+-+-家宣 6
#+-+-+-+-+-家継 7
#+-+-+-綱吉 5
#+-+-忠長
#+-+-和子
#+-+-正之
#+-忠輝
#+-義直
#+-頼信
#+-+-光貞
#+-+-+-吉宗 8
#+-+-+-+-家重 9
#+-+-+-+-+-家治 10
#+-+-+-+-+-重好
#+-+-+-+-宗武
#+-+-+-+-+-定信
#+-+-+-+-宗尹
#+-+-+-+-+-治済
#+-+-+-+-+-+-家斉 11
#+-+-+-+-+-+-+-家慶 12
#+-+-+-+-+-+-+-+-家定 13
#+-+-+-+-+-+-+-斉順
#+-+-+-+-+-+-+-+-家茂 14
#+-+-+-+-+-+-斉敦
#+-+-+-+-+-+-斉匡
#+-+-+-+-+-+-+-慶頼
#+-+-+-+-+-+-+-+-家達
#+-頼房
#+-+-頼重
#+-+-+-頼侯
#+-+-+-+-頼豊
#+-+-+-+-+-宗堯
#+-+-+-+-+-+-宗翰
#+-+-+-+-+-+-+-治保
#+-+-+-+-+-+-+-+-治紀
#+-+-+-+-+-+-+-+-+-斉昭
#+-+-+-+-+-+-+-+-+-+-慶喜 15
また、例えば、吉宗を祖とするツリーについても作ることができます。
# 吉宗を祖とした家系図(家康の家系図の一部)を作成する。
tree = ["吉宗",[]]
tree_generator(tree,parent_childs)
print(tstr(tree))
#出力
#吉宗 8
#+-家重 9
#+-+-家治 10
#+-+-重好
#+-宗武
#+-+-定信
#+-宗尹
#+-+-治済
#+-+-+-家斉 11
#+-+-+-+-家慶 12
#+-+-+-+-+-家定 13
#+-+-+-+-斉順
#+-+-+-+-+-家茂 14
#+-+-+-斉敦
#+-+-+-斉匡
#+-+-+-+-慶頼
#+-+-+-+-+-家達
6.2.6 完成版のプログラム
上のプログラムをすべて入れた、完成版のプログラムを示します。
# 親子関係を配列で表したデータ
parent_childs = [
["家康","信康"],["家康","秀康"],["家康","秀忠"],["家康","忠輝"],["家康","義直"],
["秀忠","家光"],["秀忠","忠長"],["秀忠","和子"],["秀忠","正之"],["家光","家綱"],
["家光","綱重"],["家光","綱吉"],["綱重","家宣"],["家宣","家継"],["家康","頼信"],
["頼信","光貞"],["光貞","吉宗"],["吉宗","家重"],["家重","家治"],["家重","重好"],
["吉宗","宗武"],["宗武","定信"],["吉宗","宗尹"],["宗尹","治済"],["治済","家斉"],
["治済","斉敦"],["治済","斉匡"],["家斉","家慶"],["家慶","家定"],["家斉","斉順"],
["斉順","家茂"],["斉匡","慶頼"],["慶頼","家達"],["家康","頼房"],["頼房","頼重"],
["頼重","頼侯"],["頼侯","頼豊"],["頼豊","宗堯"],["宗堯","宗翰"],["宗翰","治保"],
["治保","治紀"],["治紀","斉昭"],["斉昭","慶喜"],
]
# 歴代将軍の配列
shogun = ["家康","秀忠","家光","家綱","綱吉","家宣","家継",
"吉宗","家重","家治","家斉","家慶","家定","家茂","慶喜"]
# 名前から何代将軍かを求める。将軍ではない場合は、空文字が返る。
sno = lambda name: "" if name not in shogun else " "+str(shogun.index(name)+1)
# 祖を指定して、ツリー構造を作成する。
def tree_generator(tree,rdata):
# こから調査する対象のノード一覧
open = [tree]
# openが空になるまで繰り返す。
while(len(open)!=0):
# open の先頭を取り出す。
n = open.pop(0)
# 親子関係のデータをすべてループする。
for pc in rdata:
# 親データと調査対象データが一致する場合
if pc[0]==n[0]:
# ツリーデータを作成して、調査対象のツリーの子ノードとして追加する。
m = [pc[1],[]]
n[1].append(m)
# さらに発見された子ノードを、これから調査をする対象としてopenに登録する。
open.append(m)
pass
pass
pass
return tree
# ツリー構造の表示関数
def tstr(node,indent=""):
s = indent+str(node[0])+sno(node[0])+"\n"
for c in node[1]: # 子ノードでループ
s += tstr(c,indent+"+-")
pass
return s
# 家康を祖とした家系図を作成する。
tree = ["家康",[]]
tree_generator(tree,parent_childs)
print(tstr(tree))
#出力
#家康 1
# ...(略)...
# 吉宗を祖とした家系図(家康の家系図の一部)を作成する。
tree = ["吉宗",[]]
tree_generator(tree,parent_childs)
print(tstr(tree))
#出力
#吉宗 8
# ...(略)...
6.3 ディシジョンツリーの生成
6.3.1 子ノード一覧の調査は、エントロピーを最も下げる属性を捜すこと
6.1.2 アルゴリズムの「4. nの子ノード一覧を調査し、それらをmとする。」を、データのエントロピーを最も下げる属性を捜すことを調査とすることにより、ディシジョンツリーを生成することができます。
以下のプログラムは、1.概要編のディシジョンツリーを作るプログラムの一部です。親ノード n、親ノードに関連付けられたデータ df_nとなっています。df_nのクラス属性のエントロピーが0の場合には、これ以上の分岐がないため、このノードから先の子ノードを作成する処理は行いません。
子ノードを作成する場合には、まず、クラス属性以外のすべての属性についてその属性で分岐した場合のエントロピーの減少量を計算します。
そして最もエントロピーを現象させる属性の分岐が子ノード一覧の m を作り、次のツリー生成のためにopenに追加されます。
# openが空になるまで繰り返す。
while(len(open)!=0):
# openの先頭を取り出し、そのノードが保持しているデータを取り出しておく。
n = open.pop(0)
df_n = n["df"]
# このノードのエントロピーが0の場合、これ以上エッジを展開できないので、
# このノードからの枝分かれはしない。
if 0==entropy(df_n.iloc[:,-1]):
continue
# 分岐可能性の属性値一覧を保存する変数を作成しておく。
attrs = {}
# クラス属性の最後の列以外の属性をすべて調査する。
for attr in df_n.columns[:-1]:
# この属性で分岐する場合のエントロピーと、
# 分岐後のデータと分岐する属性値を保存する変数を作成する。
attrs[attr] = {"entropy":0,"dfs":[],"values":[]}
# この属性の取りうる値をすべて調査する。またsortedは、属性値の重複除去された配列を、
# 実行のたびに順番が入れ替わらないようにするためである。
for value in sorted(set(df_n[attr])):
# 属性値でデータをフィルタリングする。
df_m = df_n.query(attr+"=='"+value+"'")
# エントロピーを計算し、関連するデータ、値をそれぞれ保存しておく。
attrs[attr]["entropy"] += entropy(df_m.iloc[:,-1])*df_m.shape[0]/df_n.shape[0]
attrs[attr]["dfs"] += [df_m]
attrs[attr]["values"] += [value]
pass
pass
# クラス値を分離可能な属性が1つも無い場合は、このノードの調査を終了する。
if len(attrs)==0:
continue
# エントロピーが最小になる属性を取得する。
attr = min(attrs,key=lambda x:attrs[x]["entropy"])
# 分岐する属性のそれぞれの値、分岐後のデータを、ツリーとopenにそれぞれ追加する。
for d,v in zip(attrs[attr]["dfs"],attrs[attr]["values"]):
m = {"name":attr+"="+v,"edges":[],"df":d.drop(columns=attr)}
n["edges"].append(m)
open.append(m)
pass
以上で、Pythonで0からディシジョンツリーを作って理解する、の全編を終了いたします。