Go to Qiita Advent Calendar 2024 Top
LoginSignup
5
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@tky823(tky823)

C言語でニューラルネットワークの実装（５）〜モデルの構造と順伝播の実装〜

Last updated at Posted at 2019-08-22

前回まで

前回はデータセットを準備しました。今回は，モデルの構造と順伝播を実装していきます。

モデルの構造

モデルの構造についての情報を表すためのMODEL_PARAMETER型を定義します。

_struct.h
typedef struct {
    int L; //number of hidden layers
    int K; //number of classes
    int dim_in; //input dimension
    int *N_unit; //number of units
    float *(**activation)(float *a, int D); // activation function
    float (*loss)(float *y, float *t, int K); //loss function
} MODEL_PARAMETER;

MODEL_PARAMETER 型では，

  1. 隠れ層の数（ L ）
  2. 分類するクラスの数（ K ）
  3. 入力の次元（ dim_in ）
  4. 各層のユニットの数（ N_unit ）
  5. 各層の活性化関数（ activation ）
  6. 損失関数（ loss ）
    を持っています。特に活性化関数と損失関数は，条件分岐を少なくするために関数ポインタで持ちます。次の build_model 関数では，これらのパラメータを決めていきます。隠れ層の数（ L ），各層のユニットの数（ N_unit[l] ），出力層以外の活性化関数（ activation ）はいくらか変更の余地があり，この値を変えることでモデルの構造が変化します。
forward_sample.c
#define DATA_LINE 5

MODEL_PARAMETER build_model(void){
    int l;
    MODEL_PARAMETER model_parameter;
    
    model_parameter.L = 2;
    model_parameter.K = 3;
    model_parameter.dim_in = DATA_LINE * DATA_LINE;
    
    model_parameter = setup_model_parameter(model_parameter);
    
    for(l = 1; l <= model_parameter.L; l++) {
        model_parameter.N_unit[l] = 16;
    }
    
    for(l = 1; l <= model_parameter.L; l++) {
        model_parameter.activation[l] = ReLU;
    }
    
    model_parameter.activation[model_parameter.L + 1] = softmax;
    model_parameter.loss = cross_entropy;
    
    setup_parameters(model_parameter);
    
    return model_parameter;
}

なお， setup_parameters(model_parameter); は，モデルの重み $w$ や，逆伝播で重要な $\partial E / \partial a$ の配列の領域を確保する関数です。

活性化関数の再実装

順伝播の実装に入る前に，活性化関数についてもう一度考えたいと思います。第1回で実装した活性化関数はどれも $\boldsymbol{a}$ を引数にとり， $\boldsymbol{y}$ を返す関数でした。しかし，逆伝播ではどれも $\boldsymbol{a}$ を引数にとるものの，ソフトマックス関数は行列を，それ以外の関数はベクトルを返します。これでは扱いづらいので全て行列を返す関数に変更します。他の活性化関数もソフトマックス関数のように

\frac{\partial z_{d}}{\partial a_{d'}} = \begin{cases}
    h'(a_{d})  & (d = d')\\
    0 & (d \neq d')
\end{cases}

とすることで行列のように扱うことができます。
また，活性化関数の引数に順伝播のときの通常の計算か，それとも逆伝播のときの微分の計算かを指定する引数 derivative を与えます。derivative == 1 であれば逆伝播を意味します。
逆伝播の結果 $\partial \boldsymbol{z} / \partial \boldsymbol{a}$ は， 二次元配列のderivative_matrix に書き込みます。この配列 derivative_matrix の領域の確保は関数の外でしておきます。

\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{a}} = \left(\begin{matrix}
    \dfrac{\partial z_{1}}{\partial a_{1}} & \dfrac{\partial z_{1}}{\partial a_{2}} & \cdots & \dfrac{\partial z_{1}}{\partial a_{d'}} & \cdots & \dfrac{\partial z_{1}}{\partial a_{D}}\\
    \dfrac{\partial z_{2}}{\partial a_{1}} & \dfrac{\partial z_{2}}{\partial a_{2}} & \cdots & \dfrac{\partial z_{2}}{\partial a_{d'}} & \cdots & \dfrac{\partial z_{2}}{\partial a_{D}} \\
    \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\
    \dfrac{\partial z_{d}}{\partial a_{1}} & \dfrac{\partial z_{d}}{\partial a_{2}} & \cdots & \dfrac{\partial z_{d}}{\partial a_{d'}} & \cdots  & \dfrac{\partial z_{d}}{\partial a_{D}} \\
    \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\
    \dfrac{\partial z_{D}}{\partial a_{1}} & \dfrac{\partial z_{D}}{\partial a_{2}} & \cdots & \dfrac{\partial z_{D}}{\partial a_{d'}} & \cdots & \dfrac{\partial z_{D}}{\partial a_{D}}
\end{matrix}\right) \in \mathbb{R}^{D \times D}

つまり，各活性化関数の名前で名付けられた関数は，

  1. 順伝播の場合（ derivative == 0 ）は， $\boldsymbol{z} = h(\boldsymbol{a})$ を返し， derivative_matrix には何も書き込まず，
  2. 逆伝播の場合（ derivative == 1 ）は， $\partial\boldsymbol{z} / \partial \boldsymbol{a}$ を， derivative_matrix に書き込み， NULL を返す

というような実装に変更します。

1. ステップ関数

ステップ関数の微分は次のように表されます。

\frac{\partial z_{d}}{\partial a_{d'}} = 0

第1回のステップ関数の実装に，偏微分の要素を追加していきます。
※ z の領域確保は省略しているので注意。

activation_function.h
float *step(float *a, int D, int derivative, float **derivative_matrix) {
    int d, d_dash;
    float *z = NULL;
    
    if(derivative) {
        for(d = 1; d <= D; d++) {
            for(d_dash = 1; d_dash <= D; d_dash++) {
                derivative_matrix[d][d_dash] = 0.0f;
            }
        }
        return NULL;
    }
    
    z[0] = 1.0f;
    
    for(d = 1; d <= D; d++) {
        if(a[d] < 0.0f) {
            z[d] = 0.0f;
        } else {
            z[d] = 1.0f;
        }
    }
    
    return z;
}

2. シグモイド関数

シグモイド関数の微分は次のように表されます。

\frac{\partial z_{d}}{\partial a_{d'}} = \begin{cases}
    h(a_{d})(1 - h(a_{d})) & (d = d')\\
    0 & (d \neq d')
\end{cases}
activation_function.h
float *sigmoid(float *a, int D, int derivative, float **derivative_matrix) {
    int d, d_dash;
    float *z = NULL;
    z[0] = 1.0f;
    
    for(d = 1; d <= D; d++) {
        z[d] = 1.0f / (1.0f + expf(- a[d]));
    }
    
    if(derivative) {
        for(d = 1; d <= D; d++) {
            for(d_dash = 1; d_dash <= D; d_dash++) {
                derivative_matrix[d][d_dash] = 0.0f;
            }
        }
        
        for(d = 1; d <= D; d++) {
            derivative_matrix[d][d] = z[d] * (1.0f - z[d]);
        }
        
        return NULL;
    }
    
    return z;
}

3. ReLU関数

ReLU関数の微分は次のように表されます。

\frac{\partial z_{d}}{\partial a_{d'}} = \begin{cases}
    0 & (d \neq d') \\
    0 & (d = d' \mathrm{かつ} a_{d'} < 0) \\
    1 & (d = d' \mathrm{かつ} a_{d'} \geqq 0)
\end{cases}
activation_function.h
float *ReLU(float *a, int D, int derivative, float **derivative_matrix) {
    int d, d_dash;
    float *z = NULL;

    if(derivative) {
        for(d = 1; d <= D; d++) {
            for(d_dash = 1; d_dash <= D; d_dash++) {
                derivative_matrix[d][d_dash] = 0.0f;
            }
        }
        
        for(d = 1; d <= D; d++) {
            if(a[d] > 0.0f) {
                derivative_matrix[d][d] = 1.0f;
            }
        }
        
        return NULL;
    }
    
    z[0] = 1.0f;
    
    for(d = 1; d <= D; d++) {
        if(a[d] < 0.0f) {
            z[d] = 0.0f;
        } else {
            z[d] = a[d];
        }
    }
    
    return z;
}

4. ソフトマックス関数

ソフトマックス関数は指数関数 $e^{x}$ を扱うため，オーバーフローが起きる可能性があります。これを防ぐために， $a_{k}$ から定数 $C$ を引くという方法があります1。 $C > 0$ ならば， $e^{a_{k}} > e^{a_{k} - C}$
であるため，オーバーフローを防ぐことができます。

y_{k} = \frac{e^{a_{k} - C}}{{\displaystyle \sum_{k'=1}^{K}}e^{a_{k'} - C}}

この定数 $C$ は，プログラムでは

C = \max_{k}a_{k}

としています。

activation_function.h
float *softmax(float *a, int K, int derivative, float **derivative_matrix) {
    int k, k_dash;
    float *y = NULL;
    float sum_exp = 0.0f;
    float max_a = a[1];

    for(k = 2; k <= K; k++) {
        if(a[k] > max_a) {
            max_a = a[k];
        }
    }
    
    y[0] = 1.0f;
    
    for(k = 1; k <= K; k++) {
        y[k] = expf(a[k] - max_a);
        sum_exp += y[k];
    }
    
    for(k = 1; k <= K; k++) {
        y[k] /= sum_exp;
    }
    
    if(derivative) {
        for(k = 1; k <= K; k++) {
            for(k_dash = 1; k_dash < k; k_dash++) {
                derivative_matrix[k][k_dash] = -y[k] * y[k_dash];
                derivative_matrix[k_dash][k] = -y[k] * y[k_dash];
            }
            derivative_matrix[k][k] = y[k] * (1.0f - y[k]);
        }
        
        return NULL;
    }
    
    return y;
}

損失関数の再実装

損失関数も，活性化関数と同様に逆伝播の際の微分について考えます。こちらも，引数の derivative で順伝播に利用されるのか，それとも逆伝播の微分として利用されるのかを指定していきます。
逆伝播の微分の場合，引数で受け取る dE_dy に計算結果を書き込み， 0 を返します。

1. 平均二乗誤差

平均二乗誤差は，

    E = \frac{1}{D}\sum_{d=1}^{D}(t_{d} - y_{d})^{2}

で，その微分は，

    \frac{\partial E}{\partial y_{d}} = - \frac{2(t_{d} - y_{d})}{D}

でした。

loss_function.h
float mean_squared_error(float *y, float *t, int D, int derivative, float *dE_dy) {
    int d;
    float delta;
    float E = 0.0f;

    if(derivative) {
        for(d = 1; d <= D; d++) {
            dE_dy[d] = - 2.0f * (t[d] - y[d]) / (float) D;
        }
        return 0.0f;
    }

    for(d = 1; d <= D; d++) {
        delta = t[d] - y[d];
        E += delta * delta;
    }
    
    return E / (float) D;
}

2. 交差エントロピー

交差エントロピーは，

    E = -\sum_{k=1}^{K}t_{k}\log y_{k}

で，その微分は，

    \frac{\partial E}{\partial y_{k}} = - \frac{t_{k}}{y_{k}}

でした。

loss_function.h
float EPS = 1e-12;

float cross_entropy(float *y, float *t, int K, int derivative, float *dE_dy) {
    int k;
    float E = 0.0f;
    
    if(derivative) {
        for(k = 1; k <= K; k++) {
            dE_dy[k] = - t[k] / (y[k] + EPS);
        }
        return 0.0f;
    }
    
    for(k = 1; k <= K; k++) {
        E -= t[k] * logf(y[k] + EPS);
    }
    
    return E;
}

モデルの構造の再定義

活性化関数と損失関数の引数が変わったため， MODEL_PARAMETER 型を再定義します。

struct.h
typedef struct {
    int L; //number of hidden layers
    int K; //number of classes
    int dim_in; //input dimension
    int *N_unit; //number of units
    float *(**activation)(float *a, int D, int derivative, float **derivative_matrix); // activation function
    float (*loss)(float *y, float *t, int K, int derivative, float *dE_dy); //loss function
} MODEL_PARAMETER;

活性化関数と損失関数を関数ポインタで持っているため，

model_parameter.activation[3](a[3], D[3], 0, NULL) とすれば，

\boldsymbol{z}^{(3)} = h^{(3)}\left(\boldsymbol{a}^{(3)}\right)

というように計算できます（逆伝播については次回）。

順伝播の実装

モデルの構造が決定したため，順伝播を実装していきます。各層で全結合（full connection）と活性化関数を通す操作を行っていきます。
コードはこちら

0. グローバル変数

次の変数をグローバル変数で用意します。

変数 意味
x 入力データの各成分の値
D 各層のユニット数
w 各全結合における重み
a 各層の入力
z 各層の出力
y 出力層の出力
t 正解のone-hot表現
parameters.h
float *x = NULL;
int *D = NULL;
float ***w = NULL;
float **z = NULL;
float **a = NULL;
float *y = NULL;
float *t = NULL;

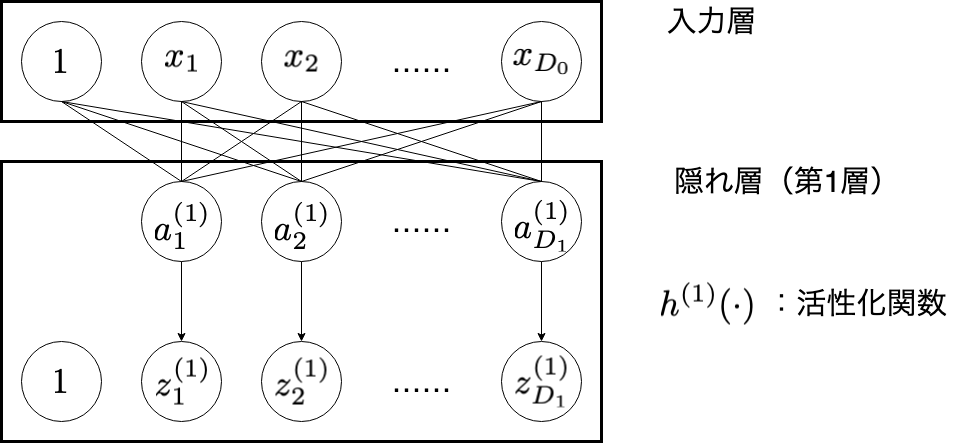
1. 入力層・隠れ層

変数 意味
$i$ 入力層のユニットのインデックス（ $i = 1, 2, \cdots , D_{0}$ ）
$j$ 隠れ層（第 $1$ 層）のユニットのインデックス（ $j = 1, 2, \cdots , D_{1}$ ）
$D_{0}$ 入力データの次元
$x_{i}$ 入力データの各成分の値
$D_{1}$ 隠れ層（第 $1$ 層）のユニットの個数
$a_{j}^{(1)}$ 隠れ層（第 $1$ 層）のユニット $j$ が受け取る値
$h^{(1)}(\cdot)$ 隠れ層（第 $1$ 層）の活性化関数
$z_{j}^{(1)}$ 隠れ層（第 $1$ 層）のユニット $j$ に活性化関数を通した出力値

input_layer.png

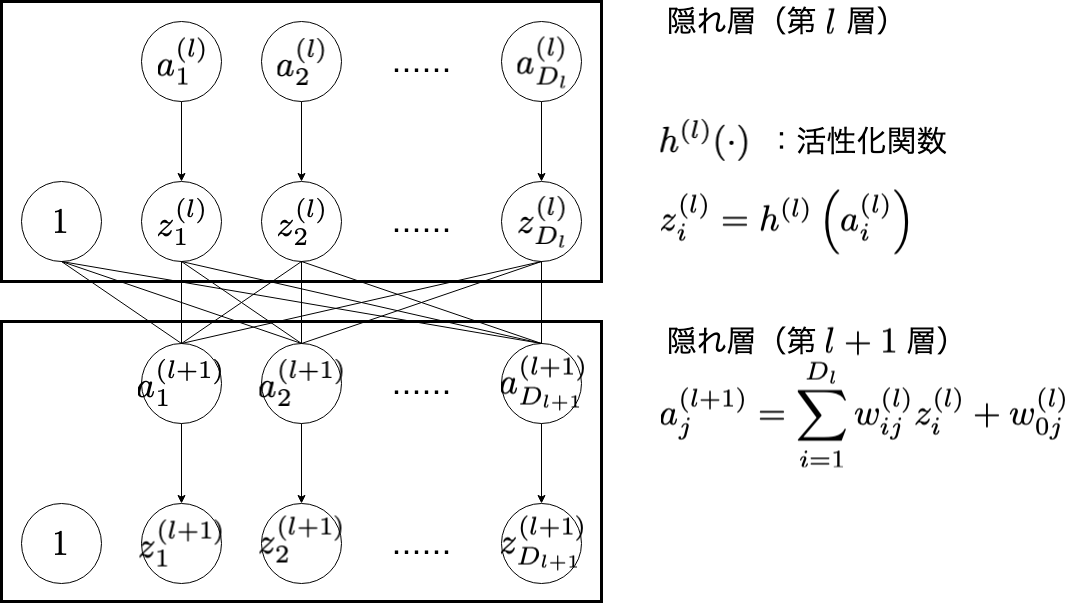
変数 意味
$l$ 隠れ層のインデックス（ $l = 1, 2, \cdots , L$ ）
$i$ 隠れ層（第 $l$ 層）のユニットのインデックス（ $i = 1, 2, \cdots , D_{l}$ ）
$a_{i}^{(l)}$ 隠れ層（第 $l$ 層）の入力
$h^{(l)}(\cdot)$ 隠れ層（第 $l$ 層）の活性化関数
$z_{i}^{(l)}$ 隠れ層（第 $l$ 層）で活性化関数を通した値
$j$ 隠れ層（第 $l + 1$ 層）のユニットのインデックス（ $j = 1, 2, \cdots , D_{l+1}$ ）
$a_{j}^{(l+1)}$ 隠れ層（第 $l + 1$ 層）の入力

hidden_layer.png

forwardsample.c
void forward(MODEL_PARAMETER model_parameter) {
    int l, i, j, k;
    int L = model_parameter.L;
    int K = model_parameter.K;
    float tmp_a;
    
    // layer: input layer
    z[0] = x;
    
    // layer: hidden layer
    for(l = 1; l <= L; l++) {
        int l_prev = l - 1;
        int d_prev_layer = D[l_prev];
        int d_max = D[l];
        
        for(j = 1; j <= d_max; j++) {
            tmp_a = w[l_prev][0][j]; //bias
            
            for(i = 1; i <= d_prev_layer; i++) {
                tmp_a += w[l_prev][i][j] * z[l_prev][i];
            }
            
            a[l][j] = tmp_a;
        }
        
        z[l] = model_parameter.activation[l](a[l], D[l], 0, NULL);
        // z[l][0] = 1.0f;
    }
    ...

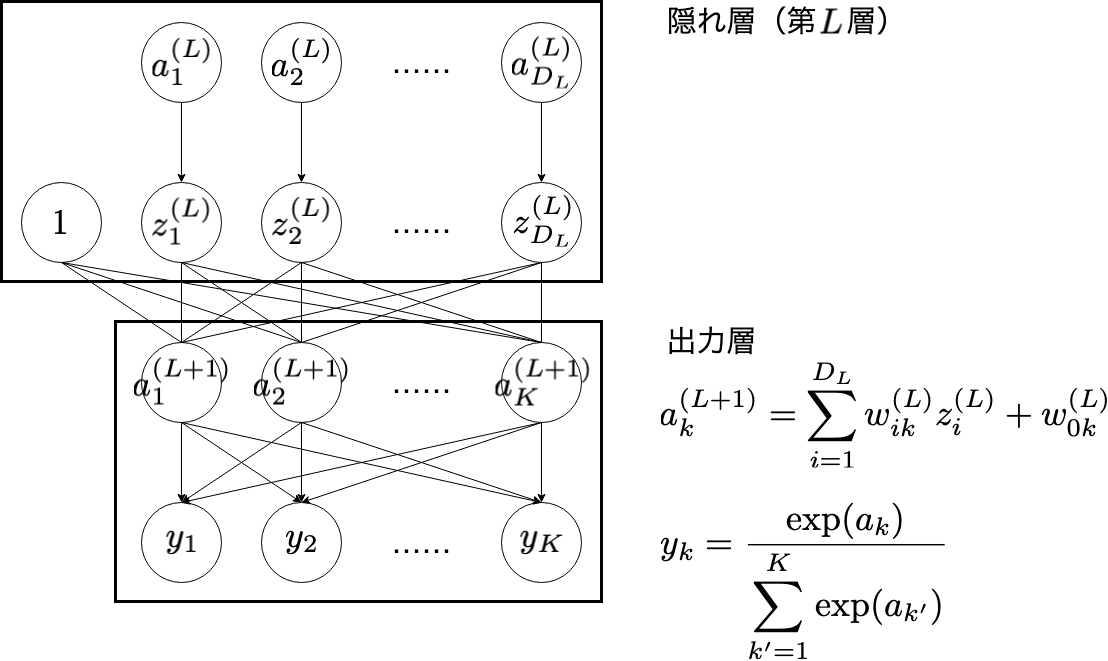
2. 出力層

変数 意味
$i$ 隠れ層（第 $L$ 層）のユニットのインデックス（ $i = 1, 2, \cdots , D_{L}$ ）
$z_{i}^{(L)}$ 隠れ層（第 $L$ 層）の出力
$k$ 出力層のユニットのインデックス（ $k = 1, 2, \cdots , K$ ）
$a_{k}^{(L+1)}$ 出力層の入力
$y_{k}$ 出力層の出力

output_layer.png

forwardsample.c
void forward(MODEL_PARAMETER model_parameter) {
    ...
    // layer: output layer
    int l_prev = L;
    int d_prev_layer = D[l_prev];
    
    for(k = 1; k <= K; k++) {
        tmp_a = w[L][0][k];
        
        for(i = 0; i <= d_prev_layer; i++) {
            tmp_a += w[L][i][k] * z[L][i];
        }
        
        a[L + 1][k] = tmp_a;
    }

    y = model_parameter.activation[L + 1](a[L + 1], K, 0, NULL);
}

forward 関数を実行することで，推測した確率 $\boldsymbol{y}$ が得られます。 forward 関数の中で，損失 $E$ を計算しても良いのですが，あえて forward 関数の外で損失の計算を行います2。

forwardsample.c
int main(int argc, char **argv) {
    int N;
    char *file_path = NULL;
    DATA *train_data = NULL;

    ...

    file_path = argv[1];
    train_data = loda_data(file_path, &N);

    MODEL_PARAMETER model_parameter = build_model();

    forward(model_parameter);
    E = model_parameter.loss(y, t, model_parameter.K, 0, NULL);
    ...
}

訓練データの1個目のデータを読み込んで損失を計算すると次のようになりました。

$ gcc forward_sample.c
$ ./a.out ../data/train_data.txt
> E: 1.102192

続き

C言語でニューラルネットワークの実装（１）〜多層パーセプトロンの構造と活性化関数〜
C言語でニューラルネットワークの実装（２）〜順伝播と損失関数〜
C言語でニューラルネットワークの実装（３）〜誤差逆伝播法〜
C言語でニューラルネットワークの実装（４）〜データの準備〜
C言語でニューラルネットワークの実装（５）〜モデルの構造と順伝播の実装〜　←現在の記事
C言語でニューラルネットワークの実装（６）〜逆伝播の実装〜
C言語でニューラルネットワークの実装（７）〜オンライン学習と重みの初期値〜
C言語でニューラルネットワークの実装（８）〜ミニバッチ学習〜

更新履歴

  • 2020/1/28 ゼロ除算を防ぐようにコードを修正しました。

  1. $ \dfrac{e^{a_{k} - C}}{{\displaystyle \sum_{k'=1}^{K}}e^{a_{k'} - C}} = \dfrac{e^{-C}e^{a_{k}}}{e^{-C}{\displaystyle \sum_{k'=1}^{K}}e^{a_{k'}}} = \dfrac{e^{a_{k}}}{{\displaystyle \sum_{k'=1}^{K}}e^{a_{k'}}}$ ↩

  2. $E$ の値は標準出力などに出力したいが，関数内で計算すると暗黙的で，計算されているのかどうかがわかりにくくなってしまうため。 ↩

5
2
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
5
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?