ニューラルネットワークの基礎を復習するために,ニューラルネットワークの一種である,多層パーセプトロンをC言語で実装してみました。
対象
C言語の読み書きができる人
ニューラルネットワークの仕組みの基礎を知りたい人
ニューラルネットワークの構造
単純パーセプトロン(simple perceptron)
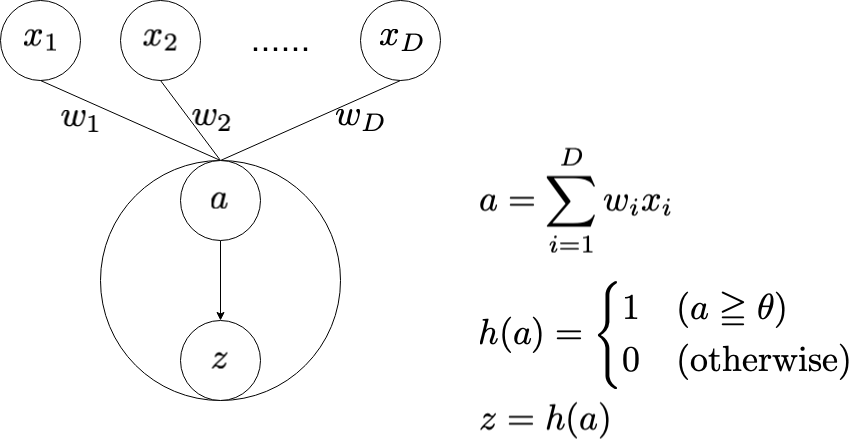
単純パーセプトロンは,もっとも小さなニューラルネットワークといえます。多次元の入力の重み付け和を計算し,その値が閾値 $\theta$ 以上であれば $1$ を,そうでなければ $0$ を出力します。
ニューラルネットにおいて,重み付け和から出力を決定する関数を活性化関数といいます。上図では $h(\cdot)$ が活性化関数に当たります。この図では,閾値 $\theta$ 以上であれば $1$ を,そうでなければ $0$ を返す関数を活性化関数として利用していますが,他にもいくつかの種類の関数があり,目的に応じて使い分けます。
多層パーセプトロン(MLP: MultiLayer Perceptron)
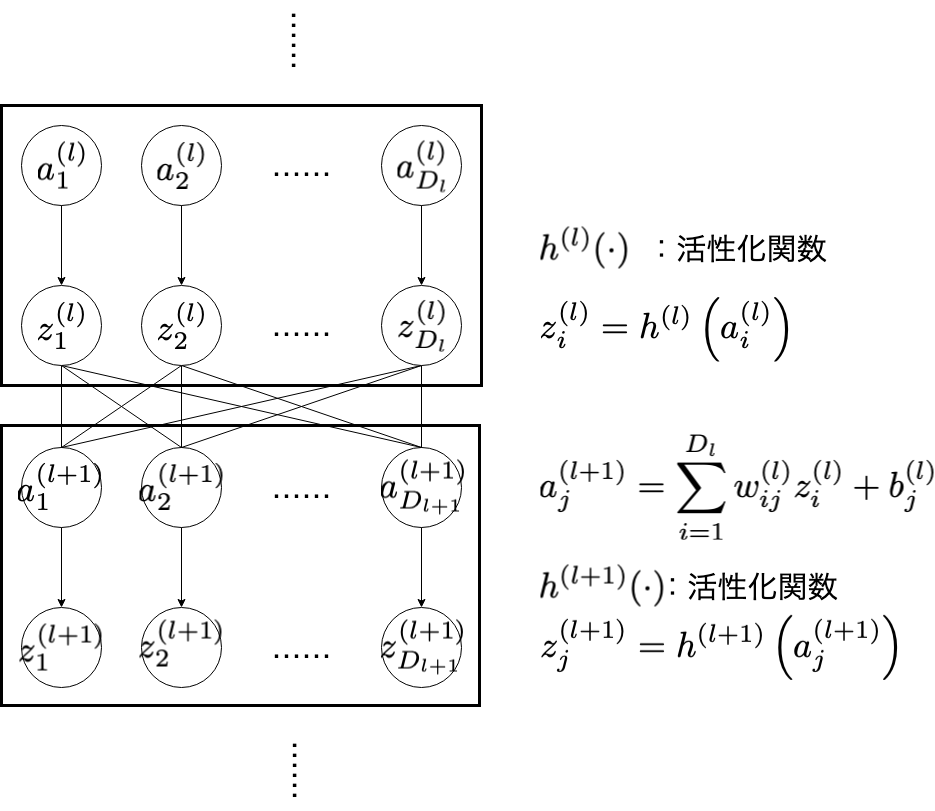
先ほどの「入力の重み付け和の計算→活性化関数に通す」という処理を多層的におこなうものが多層パーセプトロンです。重み付け和の $w_{ij}^{(l)}$ (と $b_{j}^{(l)}$ )をいい感じに調整すれば,どんな関数でも表現できるのではないか,というのが多層パーセプトロンのモチベーションです1。これをC言語で実装することが目標となっています。
活性化関数(activation function)
活性化関数は,入力に応じた活性化の様子を決める関数です。ニューロンを模しており,基本的に単調増加です。ここでは,活性化関数の代表例として,
- ステップ関数
- シグモイド関数
- ReLU関数
- ソフトマックス関数
の4つを説明します。
※各変数について
| 型 | 変数 | 意味 |
|---|---|---|
int |
D または K
|
入力,出力の次元 |
float * |
a |
入力(1次元配列)。$\boldsymbol{a} = (a_{1}, a_{2}, \cdots, a_{D})^{\top}$のイメージ |
float * |
z |
出力(1次元配列)。$\boldsymbol{z} = (z_{1}, z_{2}, \cdots, z_{D})^{\top}$のイメージ |
添字を式中に揃えて $1$ から使いたいため,動的配列のメモリ確保時にはサイズに注意する必要があります。
1. ステップ関数(step function)
ステップ関数は,次の式で定義されるような関数です。単純パーセプトロンの説明中に登場した活性化関数がこのステップ関数です。
h(\tilde{a}) = \begin{cases}
1 & \left( \tilde{a} \geqq \theta \right) \\
0 & \left( \mathrm{otherwise} \right)
\end{cases}
この $\theta$ は活性化の閾値ですが,そもそも $\tilde{a}$ にバイアス項 $b := - \theta$ を足し合わせる($a := \tilde{a} + b = \tilde{a} - \theta$)ことで,ステップ関数自体は,
h(a) = \begin{cases}
1 & \left( a \geqq 0 \right) \\
0 & \left( \mathrm{otherwise} \right)
\end{cases}
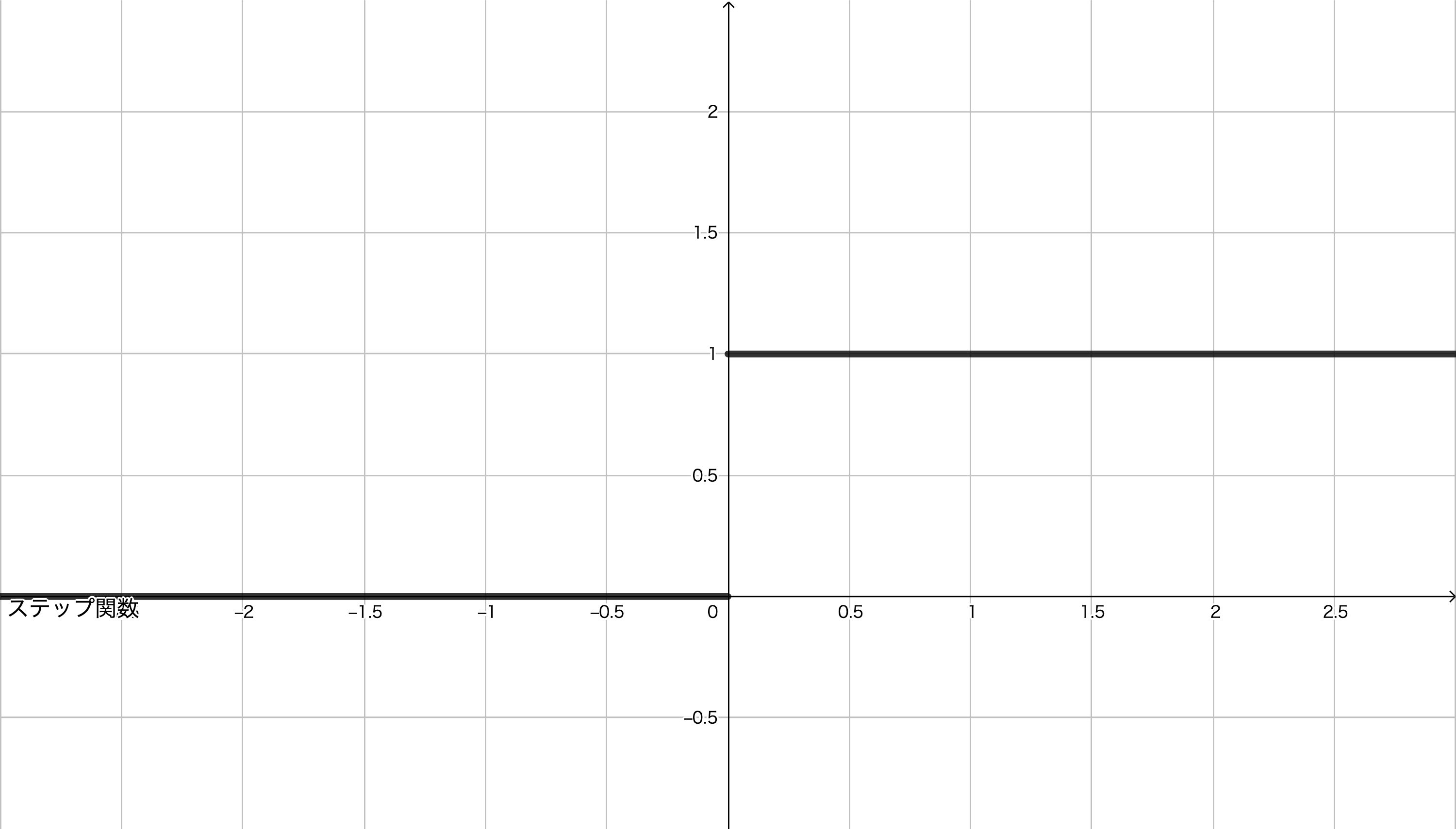
と,閾値が $0$ となっていることが多いです。これ以降の活性化関数についても $a$ の値を求める段階で,この閾値 $\theta$ や閾値に相当するものを決めるバイアスが足されているものとして扱っていきます。このステップ関数の概形は次のようになります。
さて,多層パーセプトロン中では,基本的に同じ層の活性化関数は同じ種類のものを扱います。そのため, float *型のaを受け取り,float *型のzを返すような関数として関数stepを実装します。
float *step(float *a, int D) {
int d;
float *z = NULL;
if((z = (float *)malloc((D + 1) * sizeof(float))) == NULL) {
return NULL;
}
z[0] = 0.0f;
for(d = 1; d <= D; d++) {
if(a[d] < 0.0f) {
z[d] = 0.0f;
} else {
z[d] = 1.0f;
}
}
return z;
}
2. シグモイド関数(sigmoid function)
シグモイド関数は,次の式で定義されるような関数です。
h(a) = \frac{1}{1+e^{-a}}
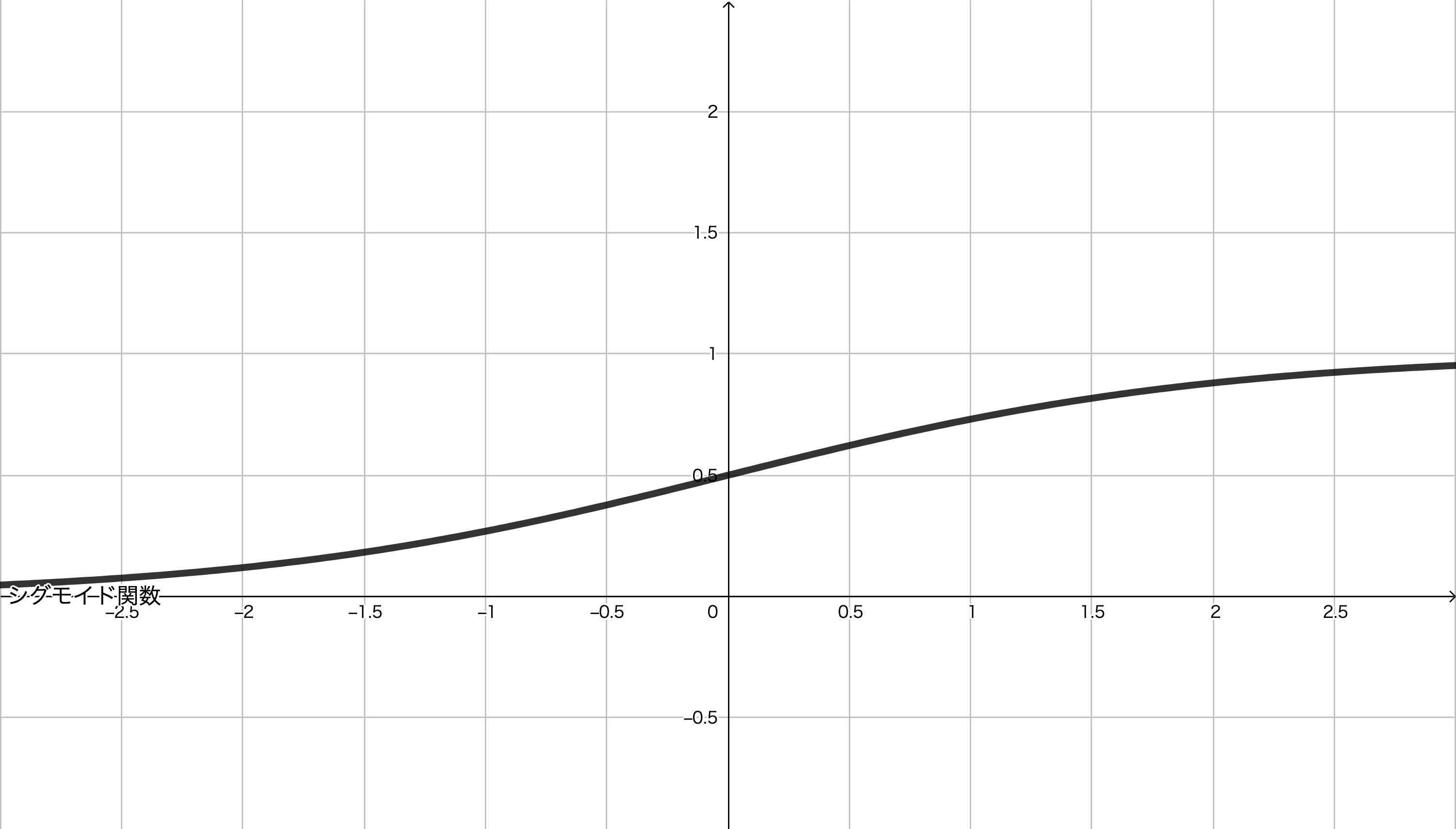
この関数の概形は次のようになります。
シグモイド関数は, $0$ から $1$ までの値をとります。そのため,確率的な出力をおこないたい場合に用いられます。
float *sigmoid(float *a, int D) {
int d;
float *z = NULL;
if((z = (float *)malloc((D + 1) * sizeof(float))) == NULL) {
return NULL;
}
z[0] = 0.0f;
for(d = 1; d <= D; d++) {
z[d] = 1.0f / (1.0f + expf(- a[d]));
}
return z;
}
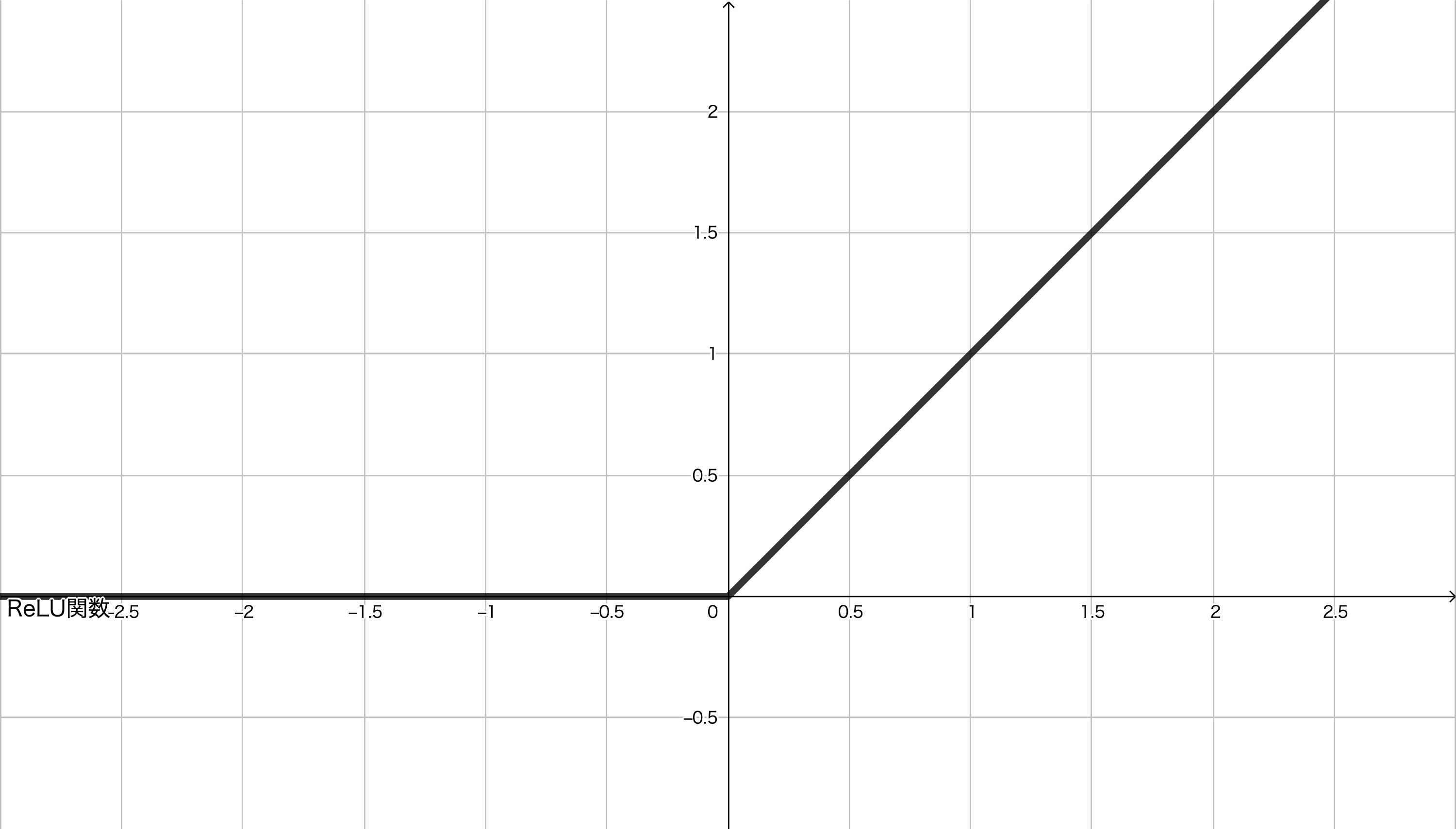
3. ReLU関数(ReLU function: Rectified Linear Unit function)
ReLU関数は,ランプ関数(ramp function)とも呼ばれます。次の式で定義されるような関数です。
h(a) = \begin{cases}
a & \left( a \geqq 0 \right) \\
0 & \left( otherwise \right)
\end{cases}
この関数の概形は次のようになります。
ステップ関数やシグモイド関数の値が $0$ から $1$ までの値に収まっているのに対して,ReLU関数は $a$ の増加とともに,上限なく増加していきます。
float *ReLU(float *a, int D) {
int d;
float *z = NULL;
if((z = (float *)malloc((D + 1) * sizeof(float))) == NULL) {
return NULL;
}
z[0] = 0.0f;
for(d = 1; d <= D; d++) {
if(a[d] < 0.0f) {
z[d] = 0.0f;
} else {
z[d] = a[d];
}
}
return z;
}
4. ソフトマックス関数(softmax function)
ソフトマックス関数は,次の式で定義されるような関数です。
\boldsymbol{z} = h(\boldsymbol{a}) \\
z_{k} = \frac{e^{a_{k}}}{{\displaystyle \sum_{k'=1}^{K}}e^{a_{k'}}}
ステップ関数,シグモイド関数,ReLU関数はスカラーを引数にとる関数でしたが,ソフトマックス関数はベクトルを引数にとります(そのため図も載せていません)。次の2つの性質を満たしていることから $K$ クラスの確率を表現でき,分類問題を解く場合の出力層の活性化関数に用いられます。
z_{k} \geqq 0 \\
\sum_{k=1}^{K}z_{k} = 1
なお, $K=2$ である場合,
z_{1} = \frac{1}{1 + e^{-a_{1}+a_{2}}} \\
z_{2} = \frac{1}{1 + e^{-a_{2}+a_{1}}} = 1 - z_{1}
とシグモイド関数の形が出てきます。
float *softmax(float *a, int K) {
int k;
float *y = NULL;
float sum_exp = 0.0f;
if((y = (float *)malloc((K + 1) * sizeof(float))) == NULL) {
return NULL;
}
y[0] = 0.0f;
for(k = 1; k <= K; k++) {
y[k] = expf(a[k]);
sum_exp += y[k];
}
for(k = 1; k <= K; k++) {
y[k] /= sum_exp;
}
return y;
}
活性化関数の実行
入力が $\boldsymbol{a} = (-2.0, -1.0, 0.0, 1.0, 2.0)^{\top}$ である場合の各活性化関数の出力は次のようになりました。出力は, $d$ 行目が入力 $a_{d}$ に対応する活性化関数の出力 $z_{d}$ です( $d = 1, 2, \cdots , 5$ )。
→ コード
=====step function=====
[
0.000000
0.000000
1.000000
1.000000
1.000000
]
=====sigmoid function=====
[
0.119203
0.268941
0.500000
0.731059
0.880797
]
=====ReLU function=====
[
0.000000
0.000000
0.000000
1.000000
2.000000
]
=====softmax function=====
[
0.011656
0.031685
0.086129
0.234122
0.636409
]
続き
C言語でニューラルネットワークの実装(1)〜多層パーセプトロンの構造と活性化関数〜 ←現在の記事
C言語でニューラルネットワークの実装(2)〜順伝播と損失関数〜
C言語でニューラルネットワークの実装(3)〜誤差逆伝播法〜
C言語でニューラルネットワークの実装(4)〜データの準備〜
C言語でニューラルネットワークの実装(5)〜モデルの構造と順伝播の実装〜
C言語でニューラルネットワークの実装(6)〜逆伝播の実装〜
C言語でニューラルネットワークの実装(7)〜オンライン学習と重みの初期値〜
C言語でニューラルネットワークの実装(8)〜ミニバッチ学習〜
参考文献
[1] ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
-
ニューラルネットワークの学習全般に言えることですが。 ↩