Go to Qiita Advent Calendar 2024 Top
LoginSignup
5
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@tky823(tky823)

C言語でニューラルネットワークの実装（８）〜ミニバッチ学習〜

Last updated at Posted at 2019-09-10

前回まで

前回はオンライン学習を実装しました。データ1個ごとに重みの計算を行うものです。これに対して今回はデータを複数計算してから重みの更新を行う手法について実装します。

損失とは

これまでに，「モデルの出力が正解とどれだけ離れているか」の指標として損失関数を定義し，ここから計算される損失を出来るだけ小さくする，ということが勾配降下法のモチベーションでした。各データごとに計算される損失の値が違うにも関わらず今までの手順で重みを更新することは，損失を小さくするという目標に沿っているのでしょうか。さらに言えば，本当に小さくしたい損失は何なのでしょうか。

回帰の例

この一連の記事で扱っていた，入力 $\boldsymbol{x}$ に対してそのクラス（離散値）を推定するような問題は，分類（classification）と呼ばれます。これに対して，入力 $\boldsymbol{x}$ に対して連続値 $t$ を推定するような問題を回帰（regression）といいます。
回帰の例をあげながら，最小化したい損失は何なのかについて考えます。ここでは回帰問題の例として，身長から体重を推定するという問題を考えてみます。
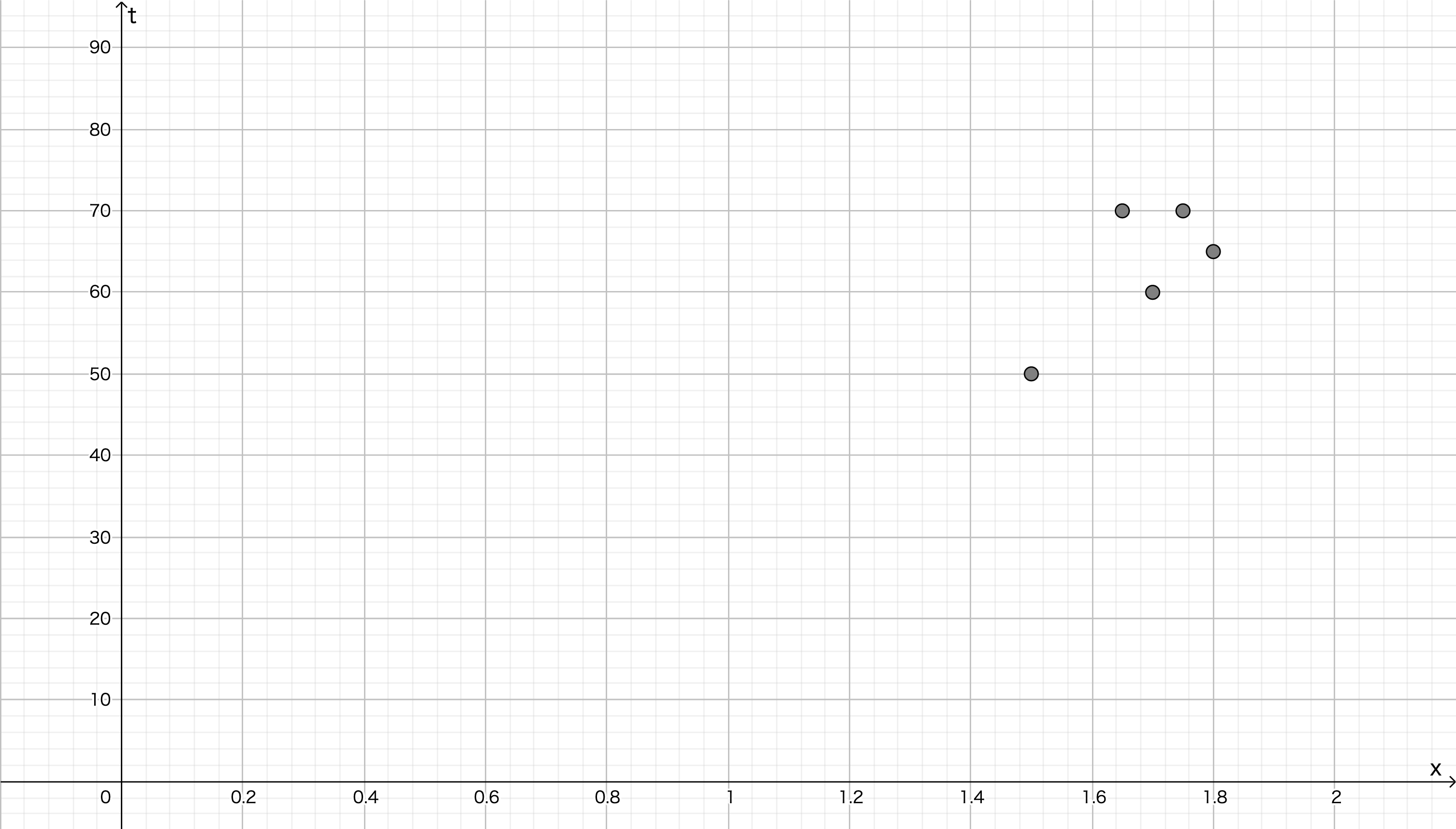
次のような5個の学習データが与えられたとします。

$x$ : 身長(m) $t$ : 体重(kg)
1.50 50.0
1.80 65.0
1.75 70.0
1.65 70.0
1.70 60.0

regression_data.png

ニューラルネットワークを構築せず，単純に $t=wx$ で近似できないかと考えてみます（ $x$：身長[m]，$t$：体重[kg] ）。実際にはありえませんが，身長 $0$ mであれば体重は必ず $0$ kgとなるはずですから， $t=wx$ はこの条件を満たしていて，仮定のそれっぽさはあります。
では，この $w$ の適切な値を見つけるために損失関数を定義します。今回は二乗誤差とします。

    E = (t-y)^{2}

勾配降下法を使って...といきたいところですが，ある一つのデータ $x^{(1)} = 1.50, t^{(1)} = 50.0$ に対する損失が最小になるような $w$ の値は簡単に求められます。 $\partial E / \partial w = 0$ を解くことで， $w = t / x$ と計算できます。

    \left.\frac{\partial E}{\partial w}\right|_{x=x^{(1)}, t=t^{(1)}} = 2(t-w^{(1)}x^{(1)})\cdot(-x^{(1)}) \\
    -2x^{(1)}(t-w^{(1)}x^{(1)}) = 0 \\
    w = \frac{t^{(1)}}{x^{(1)}}

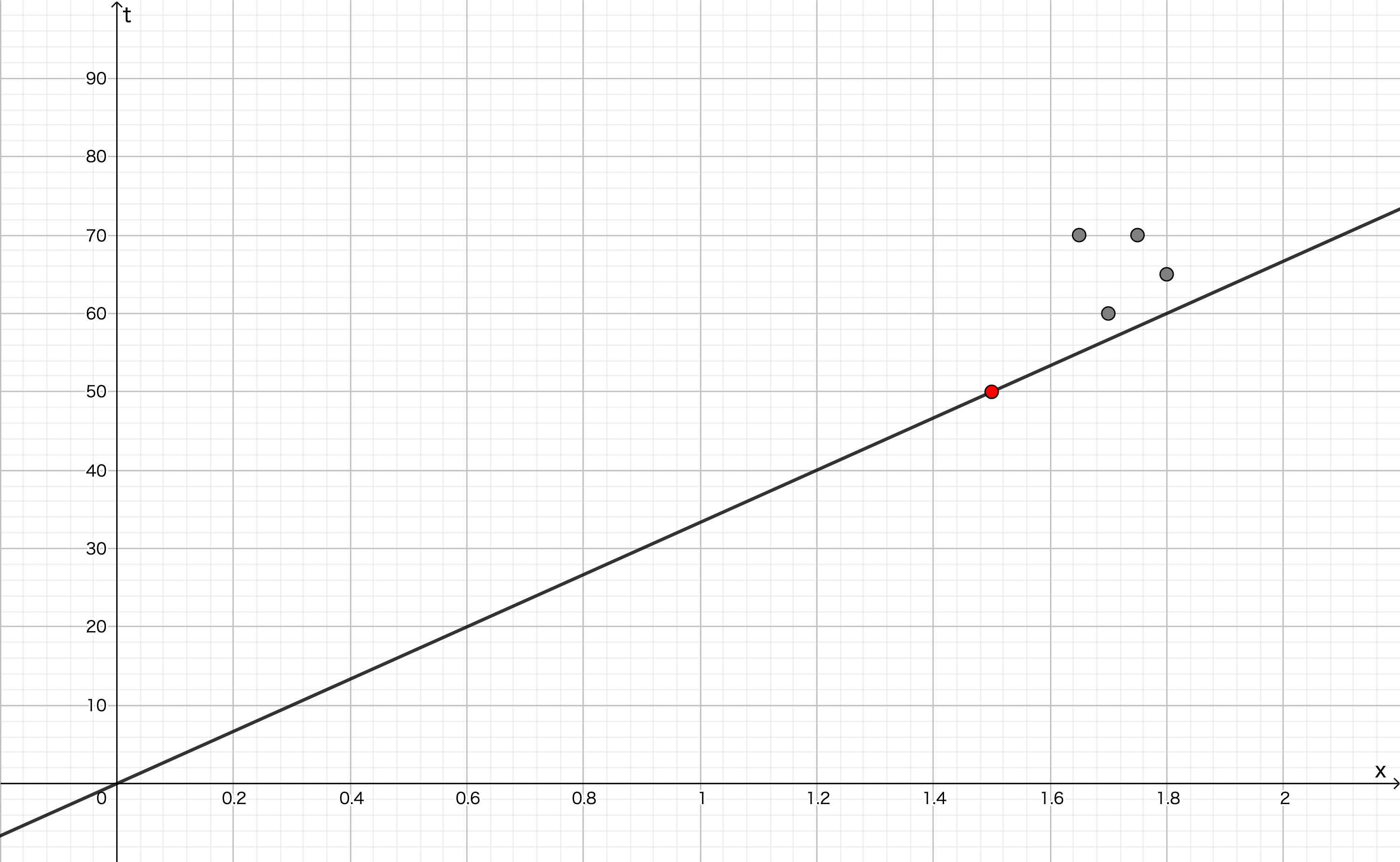
これは，原点と(1.50, 50.0)を通るような直線を求めたことになります

regression_approxiation.png

...が，この操作で求めた $w$ の値が相応しいかといえば，そんなことはありません。このデータ $x = 1.50, t = 50.0$ に対してのみ最適な値であって，他のデータにとって最適であるとは必ずしも言えません。この後，2つ目のデータに対して同じ操作をしてもこの問題は解決しません。

分布を考慮した損失関数

1つ前の節では，損失 $E$ を各データに対して $E = (t-y)^{2}$ と計算し，この最小化を考えていましたが，代わりに次の損失 $\bar{E}$ を最小化することを目標にしてみましょう。

    \bar{E} = \frac{1}{N}\sum_{n=1}^{N}\left(t^{(n)}-y^{(n)}\right)^{2}

ただし， $N$ はデータの個数で，今回の例では $N=5$ です。 $y^{(n)}$ は $n$ 個目の入力 $x^{(n)}$ に対する出力で， $t^{(n)}$ はその正解です。

これまでの扱ってきた損失を $E^{(n)}$ とすれば，

    \bar{E} = \frac{1}{N}\sum_{n=1}^{N}E^{(n)}

とも書けます。
$\bar{E}$ を偏微分して，

    \begin{align}
        \frac{\partial \bar{E}}{\partial w} & = \frac{1}{N}\sum_{n=1}^{N}\frac{\partial \bar{E}}{\partial y^{(n)}}\frac{\partial y^{(n)}}{\partial w} \\
        & = -\frac{2}{N}\sum_{n=1}^{N}\left(t^{(n)}-y^{(n)}\right)x^{(n)}
    \end{align}

これを $0$ とすることで，

w = \dfrac{{\displaystyle \sum_{n=1}^{N}}t^{(n)}x^{(n)}}{{\displaystyle \sum_{n=1}^{N}}\left\{x^{(n)}\right\}^{2}}

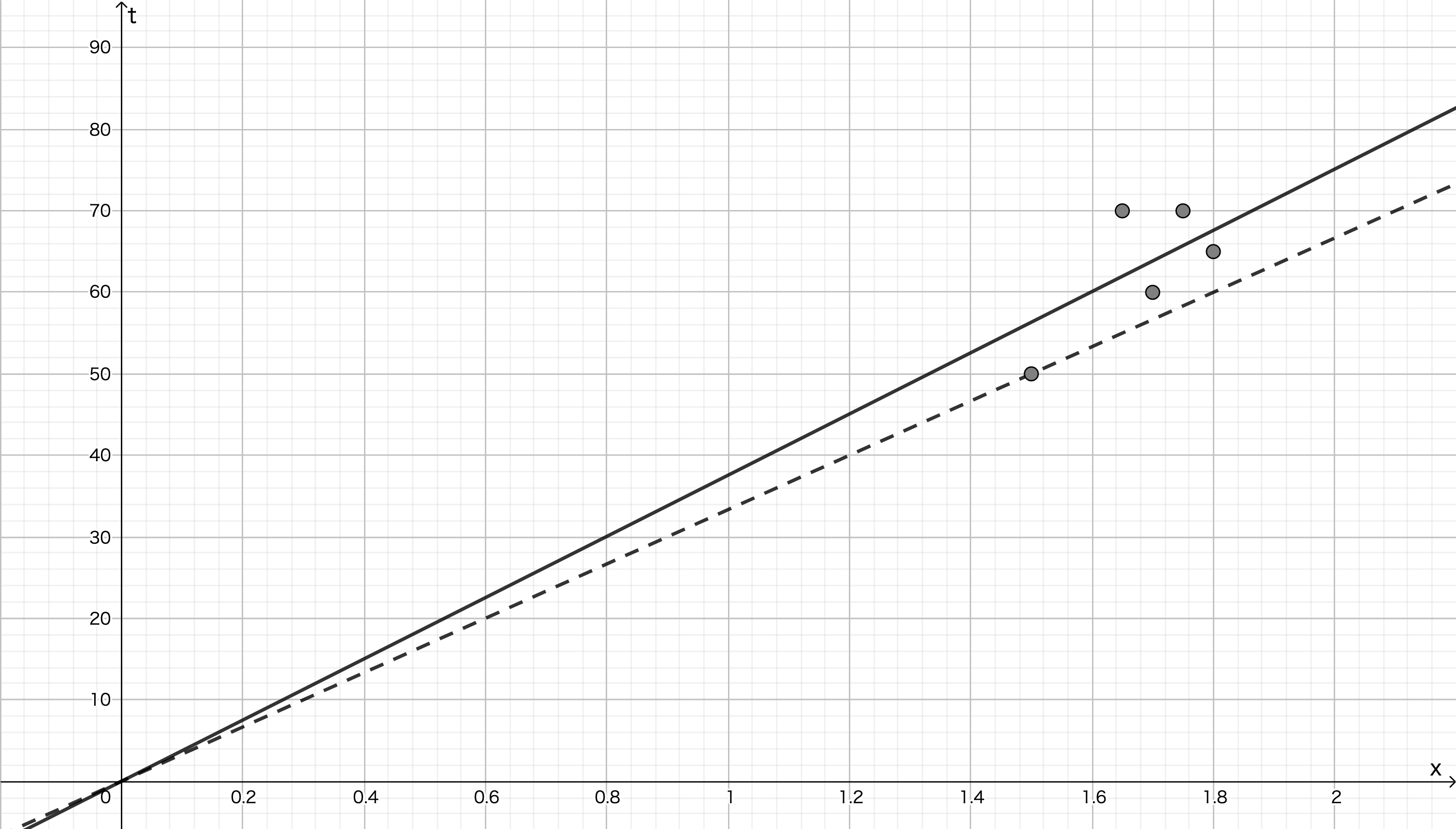
が求まります。上のデータに対して，この傾きを計算すると， $w \approx 37.6$ となります。次の図の実線がこの直線になります。破線が1個目のデータに対して最適な傾きの直線でしたが，それよりも適切そうに見えます。

regression.png

最小化

これまでに損失関数を定義してきましたが，最終的に最小化したいのは，個々の学習データ $x^{(n)}$ に対する損失を $E^{(n)}$ とすると，

    \bar{E} = \frac{1}{N}\sum_{n=1}^{N}E^{(n)}

であるとか，あるいは，学習データのみならず実際に観測されるデータの分布を考慮した

    \bar{E} = \int p(\boldsymbol{x})E(\boldsymbol{x}) d\boldsymbol{x}

を最小化したいはずでず。しかし，学習時には $p(\boldsymbol{x})$ はわかりません。そのため，学習データの分布が，テストデータや実際に観測されるデータの分布の近似としてふさわしければ，

    \bar{E} = \frac{1}{N}\sum_{n=1}^{N}E^{(n)}

の最小化を目標とした方が良さそうです。

バッチ学習

これまで， $E^{(n)}$ の最小化を損失関数としていましたが，代わりに

    \bar{E} = \frac{1}{N}\sum_{n=1}^{N}E^{(n)}

の最小化を勾配降下法で求めていきましょう。
勾配降下法では， $\partial E^{(n)} / \partial w_{ij}^{(l)}$ を計算していました（上付き添え字の意味に注意）。ここからは， $\partial \bar{E} / \partial w_{ij}^{(l)}$ を計算していきます。

    \frac{\partial \bar{E}}{\partial w_{ij}^{(l)}}  = \frac{1}{N}\sum_{n=1}^{N}\frac{\partial E^{(n)}}{\partial w_{ij}^{(l)}}

となるので，毎回計算していた $\partial E^{(n)} / \partial w_{ij}^{(l)}$ の平均をとればよいとわかります。次のコードで，バッチ（データ全体）ごとに重みを更新します。

main_batch_training.c
METRICS train_per_batch(MODEL_PARAMETER model_parameter, float learning_rate, DATA *train_data, int N_train) {
    int k, n;
    int id;
    METRICS metrics;
    
    ...
    
    if(N_train <= 0) {
        return metrics;
    }
    
    reset_dE_dw_total(model_parameter);
    
    for(n = 1; n <= N_train; n++) {
        id = n;
        x = train_data[id].x;
        
        for(k = 1; k <= model_parameter.K; k++) {
            t[k] = 0.0f;
        }
        t[train_data[id].t] = 1.0f;
        forward(model_parameter);
        metrics.E_total += model_parameter.loss(y, t, model_parameter.K, 0, NULL);
        
        ...
        
        backward(model_parameter);
    }
    
    update_parameters(model_parameter, learning_rate, N_train);
    
    ...
    
    return metrics;
}

この方法には収束が遅いというデメリットがあります。オンライン学習では1エポック回したときに重みの更新は，データの個数回分行われます。しかし，バッチ学習では1エポックで重みの更新を1回しか行えません。今回のデータも10エポック回しただけでは，次のようにまだ収束していない様子でした。

$ gcc main_batch_training.c
$ ./a.out ../data/train_data.txt ../data/validation_data.txt ../data/test_data.txt
Epoch: 1 / 10
	loss: 1.581029, accuracy: 0.332600	validation loss: 1.614799, validation accuracy: 0.310000
Epoch: 2 / 10
	loss: 1.516450, accuracy: 0.332600	validation loss: 1.552891, validation accuracy: 0.310000
Epoch: 3 / 10
	loss: 1.459650, accuracy: 0.332600	validation loss: 1.498611, validation accuracy: 0.310000
...
Epoch: 10 / 10
	loss: 1.223207, accuracy: 0.391500	validation loss: 1.270561, validation accuracy: 0.380000
Test
	accuracy: 0.470000

（100エポック回すと精度は0.6ほどになる）
バッチ学習では収束が遅いため，多く回す必要があります。また，バッチ単位で正規化を施すような処理をする1場合，バッチ全体をメモリに載せておく必要があるため，巨大でデータであれば載り切らないという問題が生じることもあります。

ミニバッチ学習

バッチ学習のメリットを利用しつつ，デメリットを解消するのがミニバッチ学習という方法です。オンライン学習とバッチ学習の中間的なポジションに位置しています。
上記のバッチ学習を32個などの小さい単位で行います。この単位をミニバッチと言い，その大きさ（データ数）をバッチサイズ（batch size）と言います。ミニバッチはデータ全体からランダムに選ばれます。

main_mini_batch_training.c
METRICS train_per_batch(MODEL_PARAMETER model_parameter, float learning_rate, int batch_size, DATA *train_data, int N_train) {
    int k, n;
    int id;
    METRICS metrics;

    ...
    
    if(batch_size <= 0) {
        return metrics;
    }
    
    reset_dE_dw_total(model_parameter);
    
    for(n = 1; n <= batch_size; n++) {
        // select at random
        id = rand() % N_train + 1;
        x = train_data[id].x;
        
        for(k = 1; k <= model_parameter.K; k++) {
            t[k] = 0.0f;
        }
        t[train_data[id].t] = 1.0f;
        forward(model_parameter);
        metrics.E_total += model_parameter.loss(y, t, model_parameter.K, 0, NULL);
        
        backward(model_parameter);
    }
    
    update_parameters(model_parameter, learning_rate, batch_size);
    
    ...

    return metrics;
}

これを回すと，

$ gcc main_mini_batch_training.c
$ ./a.out ../data/train_data.txt ../data/validation_data.txt ../data/test_data.txt
Epoch: 1 / 10
	loss: 0.840731, accuracy: 0.638500	validation loss: 0.669052, validation accuracy: 0.780000
Epoch: 2 / 10
	loss: 0.512734, accuracy: 0.837500	validation loss: 0.428381, validation accuracy: 0.900000
Epoch: 3 / 10
	loss: 0.325672, accuracy: 0.946600	validation loss: 0.285418, validation accuracy: 0.940000
...
Epoch: 10 / 10
	loss: 0.049226, accuracy: 0.997400	validation loss: 0.051535, validation accuracy: 0.990000
Test
	accuracy: 1.000000

バッチ学習よりも高い精度となりました。オンライン学習の結果と比べると劣っていますが，これはデータが単純であるためだと考えられます。実際にはミニバッチ学習を使うことが多く感じます。

まとめ

ここまで8回ダラダラとニューラルネットワークをC言語で実装してきました。普段はKerasなどで簡単に書いていますが，C言語で実装することでネットワークの構造や誤差逆伝播法の仕組みを確認できたのが，よかった点かと思います。同じことをもう一度やろうとは思いませんが...

全体のコード

コードはこちら

続き

C言語でニューラルネットワークの実装（１）〜多層パーセプトロンの構造と活性化関数〜
C言語でニューラルネットワークの実装（２）〜順伝播と損失関数〜
C言語でニューラルネットワークの実装（３）〜誤差逆伝播法〜
C言語でニューラルネットワークの実装（４）〜データの準備〜
C言語でニューラルネットワークの実装（５）〜モデルの構造と順伝播の実装〜
C言語でニューラルネットワークの実装（６）〜逆伝播の実装〜
C言語でニューラルネットワークの実装（７）〜オンライン学習と重みの初期値〜
C言語でニューラルネットワークの実装（８）〜ミニバッチ学習〜　←現在の記事

  1. Batch Normalization など ↩

5
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
5
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?