前回まで
前回は順伝播を実装しました。今回は逆伝播を実装したいと思います。
逆伝播の復習
逆伝播は次のような手順で行われました(第3回を参照)。
- 出力層で $\partial E / \partial \boldsymbol{a}^{(L+1)}$ を計算する。
- $l = L$ で, $\partial E / \partial \boldsymbol{a}^{(l+1)}$ をもとに $\partial E / \partial \boldsymbol{a}^{(l)}$ と $\partial E / \partial w^{(l)}$ を計算する。
- $l=L-1, L-2, \cdots, 1$ として2をおこなう。
- $\partial E / \partial \boldsymbol{a}^{(1)}$ をもとに $\partial E / \partial w^{(0)}$ を計算する。
- それぞれの層で $w_{ij}^{(l)}$ を更新する( $l = 0, 1, 2, \cdots, L$ )。
\frac{\partial E}{\partial w_{ij}^{(l)}} = \frac{\partial E}{\partial a_{j}^{(l+1)}}\cdot z_{i}^{(l)}
\frac{\partial E}{\partial a_{i}^{(l)}} = \frac{\partial z_{i}^{(l)}}{\partial a_{i}^{(l)}}\left(\sum_{j=1}^{D_{l+1}}\frac{\partial E}{\partial a_{j}^{(l+1)}}\cdot w_{ij}^{(l)}\right)
逆伝播の実装
次の backward 関数では,上記の1〜4までを行います。
配列で, $\partial E / \partial \boldsymbol{a}^{(l)}$ ( $l = 1, 2, \cdots, L+1$ )と $\partial E / \partial w^{(l)}$ ( $l = 0, 1, 2, \cdots, L$ )を保持しながら計算していきます。パラメータの更新に利用する式中の$\partial E / \partial \boldsymbol{a}^{(l)}$ は,グローバル変数の dE_da[l] に, $\partial E / \partial w^{(l)}$ は, dE_dw[l] に代入します。
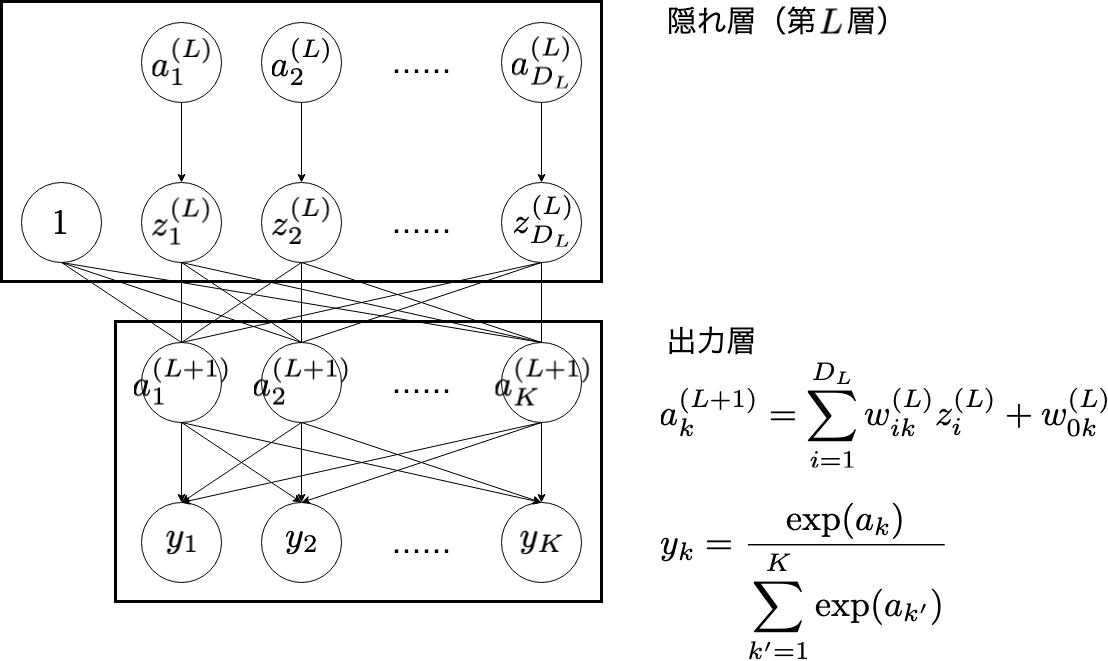
1. 出力層
このようにして計算される $\boldsymbol{y}$ に対して,最終的に損失 $E$ が計算されます。
出力層における計算では, $\partial E / \partial \boldsymbol{a}^{(L+1)}$ を得たいため,次のような順番で計算します。
\frac{\partial E}{\partial a_{k}^{(L+1)}} = \sum_{k'=1}^{K}\frac{\partial E}{\partial y_{k'}}\frac{\partial y_{k'}}{\partial a_{k}^{(L+1)}}
- $\partial E / \partial \boldsymbol{y}$ を計算
- $\partial \boldsymbol{y} / \partial \boldsymbol{a}^{(L+1)}$ を計算
- $\partial E / \partial \boldsymbol{a}^{(L+1)}$ を計算
| 変数 | 意味 |
|---|---|
dE_dy[k] |
損失関数の微分 $\partial E / \partial y_{k}$ |
dy_da[k_dash][k] |
$\partial y_{k'} / \partial a_{k}$ |
dE_da[L+1][k] |
$\partial E / \partial a^{(L+1)}_{k}$ |
void backward(MODEL_PARAMETER model_parameter) {
...
float *dE_dy, **dy_da;
// Calculate dE/dy
model_parameter.loss(y, t, K, 1, dE_dy);
/* ========== output layer ========== */
// Calculate dy/da
model_parameter.activation[L + 1](a[L + 1], K, 1, dy_da);
// Calculate dE/da
for(k = 1; k <= K; k++) {
float tmp_dE_da = 0.0f;
for(k_dash = 1; k_dash <= K; k_dash++) {
tmp_dE_da += dE_dy[k_dash] * dy_da[k_dash][k];
}
dE_da[L + 1][k] = tmp_dE_da;
}
...
}
model_parameter.loss と model_parameter.activation[L+1] は,それぞれ順伝播の際の損失関数活性化関数として扱ってきましたが,この逆伝播ではそれぞれの微分を計算するものとして扱っています。
例えば, model_parameter.loss(y, t, K, 1, dE_dy); は,4番目の引数に 1 を与えることで $\partial E / \partial \boldsymbol{y}$ の計算結果を dE_dy に書き込みます。 float * 型の戻り値( NULL )が帰ってきますが,これは使用しません。 model_parameter.activation[L + 1](a[L + 1], K, 1, dy_da) は,3番目の引数に 1 を与えることで $\partial \boldsymbol{y} / \partial \boldsymbol{a}$ の計算結果を dy_da に書き込みます。
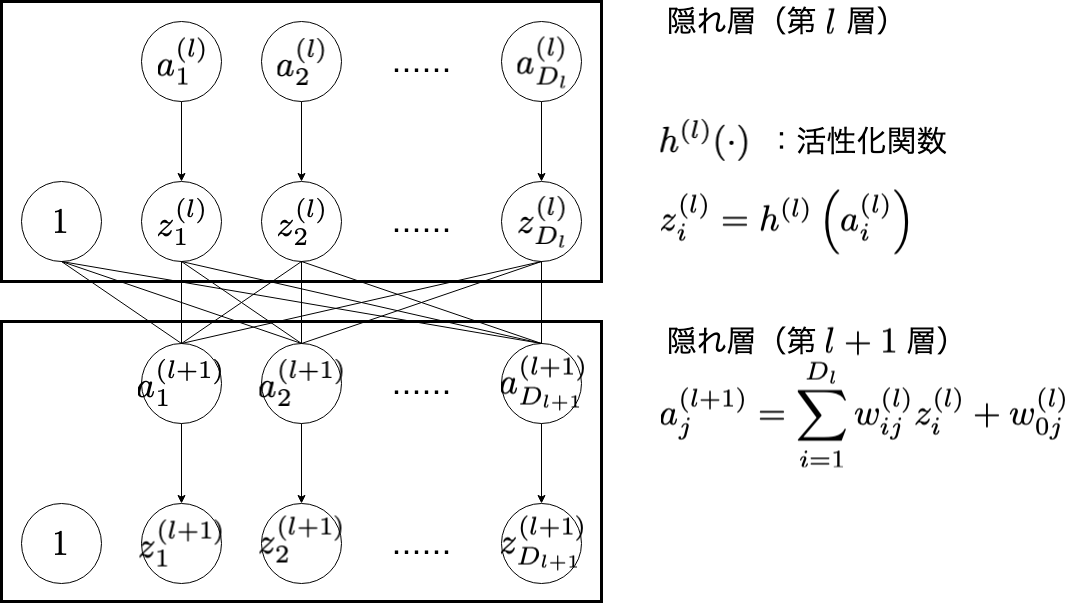
2. 隠れ層
隠れ層第 $l$ 層における計算では, $\partial E / \partial w^{(l)}$ と $\partial E / \partial \boldsymbol{a}^{(l)}$ を得ることが目標です。
\frac{\partial E}{\partial w_{ij}^{(l)}} = \frac{\partial E}{\partial a_{j}^{(l+1)}}\cdot z_{i}^{(l)}
\frac{\partial E}{\partial a_{i}^{(l)}} = h'^{(l)}(a_{i}^{(l)})\left(\sum_{j=1}^{D_{l+1}}\frac{\partial E}{\partial a_{j}^{(l+1)}}\cdot w_{ij}^{(l)}\right)
$l = L, L-1, L-2, \cdots , 1$ の順番で,次の計算をします。
- $\partial E / \partial w^{(l)}$ を計算
- $\partial \boldsymbol{z}^{(l)} / \partial \boldsymbol{a}^{(l)} = h'^{(l)}(\boldsymbol{a}^{(l)})$ を計算
- $\partial E / \partial \boldsymbol{a}^{(L)}$ を計算
| 変数 | 意味 |
|---|---|
D[l] |
隠れ層(第 $l$ 層)のユニットの数( $l = 0, 1, 2, \cdots, L$ ) |
dz_da[i][j] |
$\partial z_{i} / \partial a^{(l)}_{j}$ 。第 $l$ 層の計算中のみ使用するため,配列に l の添え字なし |
dE_da[l][i] |
$\partial E / \partial a^{(l)}_{i}$ |
dE_dw[l][i][j] |
$\partial E / \partial w^{(l)}_{ij}$ |
void backward(MODEL_PARAMETER model_parameter) {
...
float **dz_da;
...
/* ========== hidden layer ========== */
for(l = L; l >= 1; l--) {
int d_max = D[l];
int d_next_layer = D[l + 1];
float z_l_i = 0.0f; // z[l][i]
// Calculate dE/dw
for(i = 0; i <= d_max; i++) {
z_l_i = z[l][i];
for(j = 0; j <= d_next_layer; j++) {
dE_dw[l][i][j] = z_l_i * dE_da[l + 1][j];
}
}
// Calculate dz/da
model_parameter.activation[l](a[l], d_max, 1, dz_da);
// Calculate dE/da
for(i = 1; i <= d_max; i++) {
float tmp_dE_da = 0.0f;
for(j = 1; j <= d_next_layer; j++) {
tmp_dE_da += w[l][i][j] * dE_da[l + 1][j];
}
dE_da[l][i] = dz_da[i][i] * tmp_dE_da;
}
}
...
}
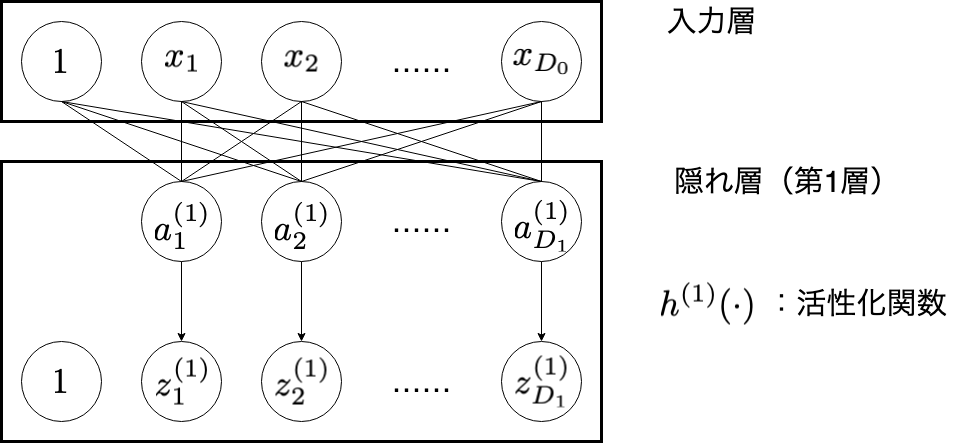
3. 入力層
入力層における計算では, $\partial E / \partial w^{(0)}$ を得ることが目標です。
\frac{\partial E}{\partial w_{ij}^{(0)}} = \frac{\partial E}{\partial a_{j}^{(1)}} \cdot x_{i}
| 変数 | 意味 |
|---|---|
model_parameter.dim_in |
入力の次元 |
z[0][i] |
$x_{i}$ |
dE_da[1][j] |
$\partial E / \partial a^{(1)}_{j}$ |
dE_dw[0][i][j] |
$\partial E / \partial w^{(0)}_{ij}$ |
void backward(MODEL_PARAMETER model_parameter) {
...
/* ========== input layer ========== */
// Calculate dE/dw
int d_max = model_parameter.dim_in;
int d_next_layer = D[1];
int z_0_i = 0.0f; // z[0][i]
for(i = 0; i <= d_max; i++) {
z_0_i = z[0][i];
for(j = 0; j <= d_next_layer; j++) {
dE_dw[0][i][j] = z_0_i * dE_da[1][j];
}
}
}
ここまでの backward 関数により, $\partial E / \partial w^{(l)}$ ( $l=0, 1, 2, \cdots, L$ )が計算されます。
w の更新
計算された $\partial E / \partial w^{(l)}$ をもとに, $w^{(l)}$ を更新していきます。更新式は次のようなものでした。
w^{(l)}_{ij} \leftarrow w^{(l)}_{ij} - \eta \frac{\partial E}{\partial w^{(l)}_{ij}}
次の update_parameters 関数で更新します。
| 変数 | 意味 |
|---|---|
learning_rate |
学習率 $\eta$ |
D[l] |
隠れ層(第 $l$ 層)のユニットの数( $l = 0, 1, 2, \cdots, L$ ) |
void update_parameters(MODEL_PARAMETER model_parameter, float learning_rate) {
int l, i, j;
int L = model_parameter.L;
for(l = 0; l <= L; l++) {
int d_max = D[l];
int d_next_layer = D[l + 1];
for(i = 1; i <= d_max; i++) {
for(j = 0; j <= d_next_layer; j++) {
w[l][i][j] -= learning_rate * dE_dw_total[l][i][j];
}
}
}
}
学習
ここまで,
- 順伝播(
forward) - 逆伝播(
backward) - 重みの更新(
update_parameters)
の関数を実装したので,この流れを各入力データに対してそれぞれ1回ずつおこなってみます1。
int main(int argc, char **argv) {
...
for(n = 1; n <= N_train; n++) {
id = rand() % N_train + 1;
x = train_data[id].x;
for(k = 1; k <= model_parameter.K; k++) {
t[k] = 0.0f;
}
t[train_data[id].t] = 1.0f;
forward(model_parameter);
E = model_parameter.loss(y, t, model_parameter.K, 0, NULL);
if(n % 100 == 0) {
printf("%d / %d E: %f\n", n, N_train, E);
}
backward(model_parameter);
update_parameters(model_parameter, LEARNING_RATE);
}
...
}
実行すると以下のようになりました。
$ gcc forward_backward_sample.c
$ ./a.out ../data/train_data.txt
100 / 10000 E: 1.786793
200 / 10000 E: 1.336350
300 / 10000 E: 0.978626
...
9900 / 10000 E: 0.001224
10000 / 10000 E: 0.002629
上の表示は (訓練データの何番目か)/(総訓練データ数) E: (そのデータでの損失の計算結果) を意味しています。データ全体としてみると,損失は減少していることがわかります。
全体のコード
コードはこちら
続き
C言語でニューラルネットワークの実装(1)〜多層パーセプトロンの構造と活性化関数〜
C言語でニューラルネットワークの実装(2)〜順伝播と損失関数〜
C言語でニューラルネットワークの実装(3)〜誤差逆伝播法〜
C言語でニューラルネットワークの実装(4)〜データの準備〜
C言語でニューラルネットワークの実装(5)〜モデルの構造と順伝播の実装〜
C言語でニューラルネットワークの実装(6)〜逆伝播の実装〜 ←現在の記事
C言語でニューラルネットワークの実装(7)〜オンライン学習と重みの初期値〜
C言語でニューラルネットワークの実装(8)〜ミニバッチ学習〜
-
実際には「各データセット全体を全て見る」という操作を複数回繰り返すことが多いです。 ↩