More than 3 years have passed since last update.

C言語でニューラルネットワークの実装（３）〜誤差逆伝播法〜

Last updated at 2021-01-28Posted at 2019-08-10

前回まで

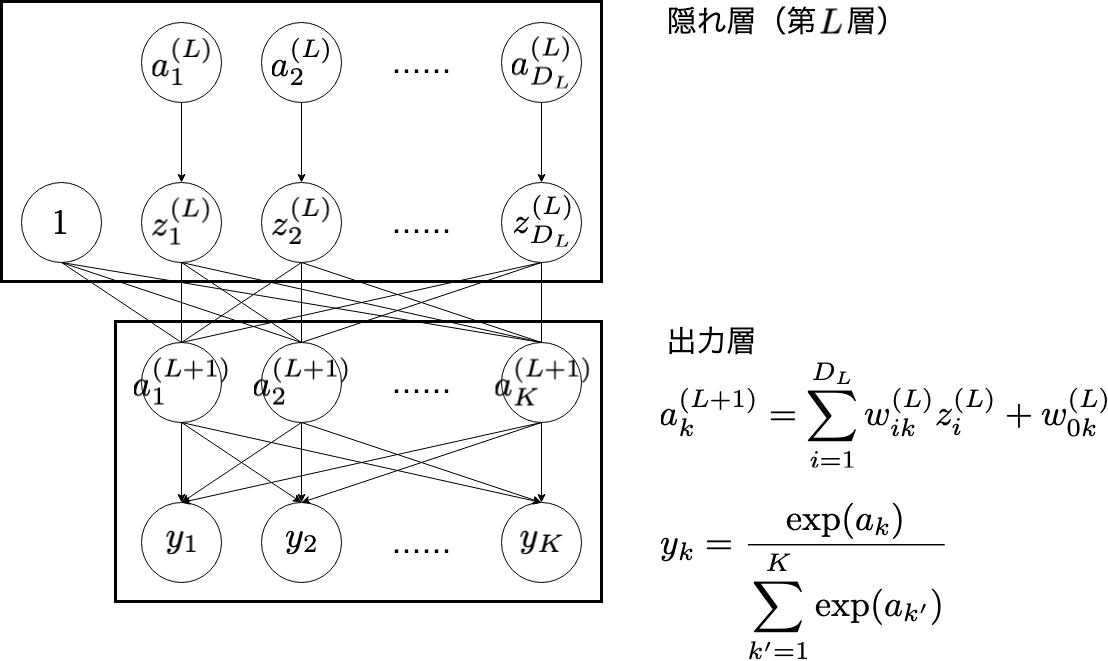
前回は順伝播と損失関数を確認しました。多クラス分類において出力層では， $\boldsymbol{y} = (y_{1}, y_{2}, \cdots, y_{K})^{\top}$ が出力され，そこから損失 $E$ が得られるということでした。今回はこの損失から，ニューラルネットワークのパラメータ $w_{ij}^{(l)}$ をどのように更新するのかについて書いていきます。

パラメータの更新

ニューラルネットワークにおけるパラメータの更新には，確率的勾配降下法（SGD: Stochastic Gradient Descent）などの勾配降下法が用いられます。これは，勾配 $\partial E / \partial w$ の情報をもとにパラメータ $w$ を更新することで，損失が小さくなるパラメータが見つけられるのではないかという考え方です¹。 $\tau$ 回目のパラメータの値を $w^{(\tau)}$ （これまでと上付き括弧の意味が異なる点に注意）とすると $\tau + 1$ 回目のパラメータ $w^{(\tau + 1)}$ は次のように計算されます。

w^{(\tau + 1)} = w^{(\tau)} - \eta \frac{\partial E}{\partial w}\left( w^{(\tau)} \right)

ここで， $\eta$ は学習率（learning rate）と呼ばれ，どの程度パラメータを更新するかを決定するハイパーパラメータです。

誤差逆伝播法（backpropagation）

誤差逆伝播法とは，出力層の出力から計算された損失をもとに，各層のパラメータを更新していくアルゴリズムです。出力層に近い方から入力層方向へと損失が伝播していくことからこの名前となっています。そのため，「出力層」→「隠れ層」→「入力層」の順でパラメータの更新について見ていきたいと思います。

1. 出力層

出力層付近の $w_{ik}^{(L)}$ の更新について考えてみます。

もし， $E$ を $w_{ik}^{(L)}$ で偏微分した関数がわかれば，勾配降下法の考え方から次のように $w_{ik}^{(L)}$ を更新することができます。

w_{ik}^{(L)} \leftarrow w_{ik}^{(L)} - \eta \dfrac{\partial E}{\partial w_{ik}^{(L)}}

では，偏微分された式を実際に計算します。偏微分の連鎖律（chain rule）²，または，合成関数の微分³から

\frac{\partial E}{\partial w_{ik}^{(L)}} = \frac{\partial E}{\partial a_{k}^{(L+1)}}\frac{\partial a_{k}^{(L+1)}}{\partial w_{ik}^{(L)}}

と分解できます。ここで，

a_{k}^{(L+1)} = \sum_{i=1}^{D_{L}}w_{ik}^{(L)}z_{i}^{(L)} + w_{0k}^{(L)}

であることから，

\frac{\partial a_{k}^{(L+1)}}{\partial w_{ik}^{(L)}} = z_{i}^{(L)}

と表されます。ただし， $z_{0}^{(L)} = 1$ とします。
では今度は， $\partial E / \partial a_{k}^{(L+1)}$ に着目してみます。

\frac{\partial E}{\partial a_{k}^{(L+1)}} = \sum_{k'=1}^{K}\frac{\partial E}{\partial y_{k'}}\frac{\partial y_{k'}}{\partial a_{k}^{(L+1)}}

とさらに分解することができます。 $\partial E / \partial y_{k'}$ は損失関数の微分を， $\partial y_{k'} / \partial a_{k}^{(L+1)}$ は出力層の活性化関数の微分を意味しています。
着色して見やすくすると次のような関係になっています。

この節では，まず損失関数の微分について考えてみます。活性化関数の微分については次の節（2. 隠れ層）で具体的な形を示したいと思います。

損失関数の微分

コードはこちら

1. 平均二乗誤差

平均二乗誤差は，

E = \frac{1}{D}\sum_{d=1}^{D}(y_{d} - t_{d})^{2}

でした。この関数を微分すると，

\frac{\partial E}{\partial y_{d}} = \frac{2(y_{d} - t_{d})}{D}

となります。次に示すコード片は， $\partial E / \partial \boldsymbol{y}$ を返す関数 d_mean_squared_error です。

\frac{\partial E}{\partial \boldsymbol{y}} = \left(\frac{\partial E}{\partial y_{1}}, \frac{\partial E}{\partial y_{2}}, \cdots, \frac{\partial E}{\partial y_{D}} \right)^{\top} \in \mathbb{R}^{D}

_loss_function.h

float *d_mean_squared_error(float *y, float *t, int D) {
    int d;
    float *dE_dy = NULL;
    
    if((dE_dy = (float *)malloc((D + 1) * sizeof(float))) == NULL) {
        exit(-1);
    }
    
    dE_dy[0] = 0.0f;
    
    for(d = 1; d <= D; d++) {
        dE_dy[d] = 2.0f * (t[d] - y[d]) / (float) D;
    }
    
    return dE_dy;
}

2. 交差エントロピー

交差エントロピーは次の式で表されました。

E = - \sum_{k=1}^{K}t_{k}\log y_{k}

この関数を微分すると，

\frac{\partial E}{\partial y_{k}} = -\frac{t_{k}}{y_{k}}

となります。次に示すコード片は， $\partial E / \partial \boldsymbol{y}$ を返す関数 d_cross_entropy です。ただし，ゼロ除算が発生しないように微小な値$\varepsilon$を分母に加えています．

_loss_function.h

float EPS = 1e-12;

float *d_cross_entropy(float *y, float *t, int K) {
    int k;
    float *dE_dy = NULL;
    
    if((dE_dy = (float *)malloc((K + 1) * sizeof(float))) == NULL) {
        exit(-1);
    }
    
    dE_dy[0] = 0.0f;
    
    for(k = 1; k <= K; k++) {
        dE_dy[k] = - (t[k] / (y[k] + EPS));
    }
    
    return dE_dy;
}

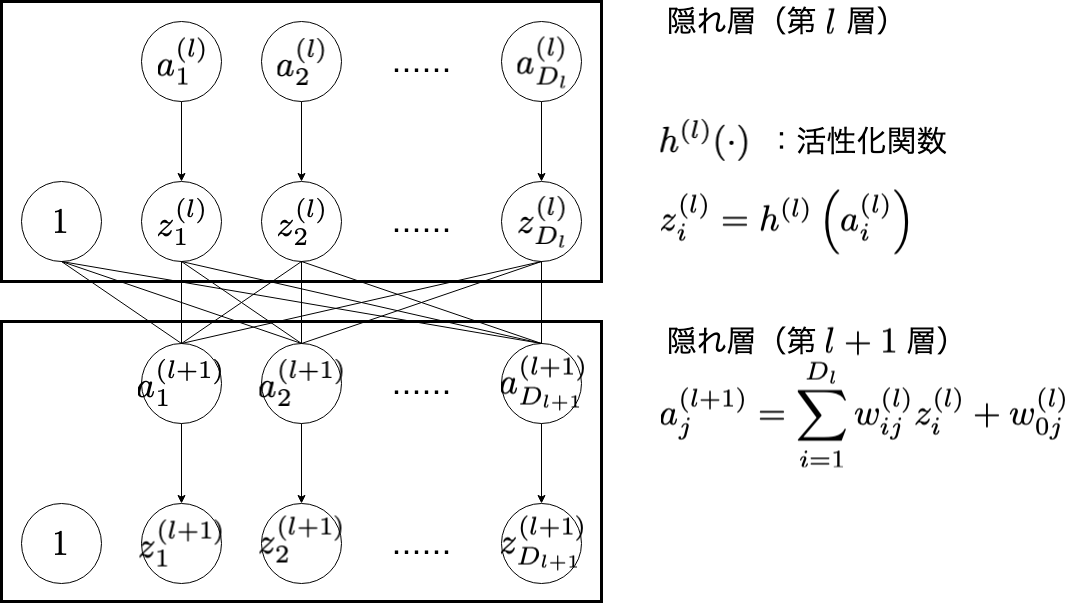
2. 隠れ層

隠れ層の $w_{ij}^{(l)}$ の更新について考えてみます。

出力層での話と同様に，次の式で $w_{ij}^{(l)}$ を更新することができます。

w_{ij}^{(l)} \leftarrow w_{ij}^{(l)} - \eta \frac{\partial E}{\partial w_{ij}^{(l)}}

偏微分の連鎖律から， $l = 0, 1, 2, \cdots, L$ の場合，

\frac{\partial E}{\partial w_{ij}^{(l)}} = \frac{\partial E}{\partial a_{j}^{(l+1)}}\frac{\partial a_{j}^{(l+1)}}{\partial w_{ij}^{(l)}}

と分解することができます。後半部分の $\partial a_{j}^{(l+1)} / \partial w_{ij}^{(l)}$ は，

\frac{\partial a_{j}^{(l+1)}}{\partial w_{ij}^{(l)}} = z_{i}^{(l)}

です（ただし， $z_{0}^{(l)} = 1$ ）。前半部分の $\partial E / \partial a_{i}^{(l)}$ について，考えてみたいと思います。各種の添字に注意してください。

\frac{\partial E}{\partial a_{i}^{(l)}} = \left(\sum_{j=1}^{D_{l+1}}\frac{\partial E}{\partial a_{j}^{(l+1)}}\frac{\partial a_{j}^{(l+1)}}{\partial z_{i}^{(l)}}\right)\frac{\partial z_{i}^{(l)}}{\partial a_{i}^{(l)}}

と変形することができます。さらにこの偏微分について， $\partial z_{i}^{(l)} / \partial a_{i}^{(l)}$ は第 $l$ 層の活性化関数の微分で

\frac{\partial z_{i}^{(l)}}{\partial a_{i}^{(l)}} = h'^{(l)}(a_{i}^{(l)})

となります。また， $\partial a_{j}^{(l+1)} / \partial z_{i}^{(l)}$ は，

\frac{\partial a_{j}^{(l+1)}}{\partial z_{i}^{(l)}} = w_{ij}^{(l)}

となるので，結果的に

\frac{\partial E}{\partial a_{i}^{(l)}} = h'^{(l)}(a_{i}^{(l)})\left(\sum_{j=1}^{D_{l+1}}\frac{\partial E}{\partial a_{j}^{(l+1)}}\cdot w_{ij}^{(l)}\right)

と整理することができます。つまり， $\partial E / \partial \boldsymbol{a}^{(l)}$ は， $\partial E / \partial \boldsymbol{a}^{(l+1)}$ の計算を利用していることになります。この部分を見ると逆伝播している様子がわかりやすいと思います。
実装の際には，

出力層で $\partial E / \partial \boldsymbol{a}^{(L+1)}$ を計算する。
$l = L$ で， $\partial E / \partial \boldsymbol{a}^{(l+1)}$ をもとに $\partial E / \partial \boldsymbol{a}^{(l)}$ と $\partial E / \partial w^{(l)}$ を計算する。
$l=L-1, L-2, \cdots, 1$ として2をおこなう。
$\partial E / \partial \boldsymbol{a}^{(1)}$ をもとに $\partial E / \partial w^{(0)}$ を計算する（入力層と隠れ層第1層の間であるため，次の節でも説明）。
それぞれの層で $w_{ij}^{(l)}$ を更新する（ $l = 0, 1, 2, \cdots, L$ ）。
というステップで計算をおこないます（重要）。また，配列などで， $\partial E / \partial \boldsymbol{a}^{(l)}$
（ $l = 1, 2, \cdots, L+1$ ）と $\partial E / \partial w^{(l)}$ （ $l = 0, 1, 2, \cdots, L$ ）を保持しておく必要があります。

（この図で「1つ前の層」というのは，ある層から見て出力層方向に1つ先にある層のことを指します。）

活性化関数の微分

$h'^{(l)}(a_{i}^{(l)})$ は，活性化関数の微分になります。C言語でニューラルネットワークの実装（１）〜多層パーセプトロンの構造と活性化関数〜で説明した4種類の関数について考えます。説明の都合上，ソフトマックス関数から説明します。
コードはこちら

1. ソフトマックス関数

ソフトマックス関数とは次のような式で表される関数でした。

\boldsymbol{z} = h(\boldsymbol{a})\\
z_{k} = \frac{e^{a_{k}}}{{\displaystyle \sum_{k'=1}^{K}}e^{a_{k'}}}

ソフトマックス関数の微分は，場合分けをする必要があります。

\frac{\partial z_{k}}{\partial a_{k'}} = \begin{cases}
    z_{k}(1 - z_{k})  & (k = k')\\
    - z_{k}z_{k'} & (k \neq k')
\end{cases}

これを，

\frac{\partial \boldsymbol{z}}{\partial \boldsymbol{a}} = \left(\begin{matrix}
    \dfrac{\partial z_{1}}{\partial a_{1}} & \dfrac{\partial z_{1}}{\partial a_{2}} & \cdots & \dfrac{\partial z_{1}}{\partial a_{k'}} & \cdots & \dfrac{\partial z_{1}}{\partial a_{K}}\\
    \dfrac{\partial z_{2}}{\partial a_{1}} & \dfrac{\partial z_{2}}{\partial a_{2}} & \cdots & \dfrac{\partial z_{2}}{\partial a_{k'}} & \cdots & \dfrac{\partial z_{2}}{\partial a_{K}} \\
    \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\
    \dfrac{\partial z_{k}}{\partial a_{1}} & \dfrac{\partial z_{k}}{\partial a_{2}} & \cdots & \dfrac{\partial z_{k}}{\partial a_{k'}} & \cdots  & \dfrac{\partial z_{k}}{\partial a_{K}} \\
    \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\
    \dfrac{\partial z_{K}}{\partial a_{1}} & \dfrac{\partial z_{K}}{\partial a_{2}} & \cdots & \dfrac{\partial z_{K}}{\partial a_{k'}} & \cdots & \dfrac{\partial z_{K}}{\partial a_{K}}
\end{matrix}\right)

というような行列の表現で考えます。この行列を返すような関数 d_softmax を以下のように実装しました。

_activation_function.h

float **d_softmax(float *a, int K) {
    int k, k_dash;
    float *y = NULL;
    float **dz_da = NULL;
    float sum_exp = 0.0f;
    float max_a = a[1];
    
    if((y = (float *)malloc((K + 1) * sizeof(float))) == NULL) {
        return NULL;
    }

    if((dz_da = (float **)malloc((K + 1) * sizeof(float *))) == NULL) {
        return NULL;
    }

    dz_da[0] = NULL;

    for(k = 1; k <= K; k++) {
        if((dz_da[k] = (float *)malloc((K + 1) * sizeof(float))) == NULL) {
            return NULL;
        }
    }

    for(k = 2; k <= K; k++) {
        if(a[k] > max_a) {
            max_a = a[k];
        }
    }
    
    for(k = 1; k <= K; k++) {
        y[k] = expf(a[k] - max_a);
        sum_exp += y[k];
    }
    
    for(k = 1; k <= K; k++) {
        y[k] /= sum_exp;
    }
    
    
    for(k = 1; k <= K; k++) {
        dz_da[k][0] = 0.0f;

        for(k_dash = 1; k_dash < k; k_dash++) {
            dz_da[k][k_dash] = -y[k] * y[k_dash];
            dz_da[k_dash][k] = -y[k] * y[k_dash];
        }
        dz_da[k][k] = y[k] * (1.0f - y[k]);
    }
    
    return dz_da;
}

2. ステップ関数

ステップ関数は次のような関数でした。

h(a) = \begin{cases}
    1 & \left( a \geqq 0 \right) \\
    0 & \left( \mathrm{otherwise} \right)
\end{cases}

微分は当然

h'(a) = 0

となります。ただし， $h'(0)$ での振る舞いに関しては，例外を設けることがあるかもしれません。各層で $z_{d} = h(a_{d})$ のため次のように書くこともできます。

\frac{\partial z_{d}}{\partial a_{d}} =  0

ステップ関数からReLU関数までは， $(\partial z_{1} / \partial a_{1}, \partial z_{2} / \partial a_{2}, \cdots, \partial z_{D} / \partial a_{D})^{\top} \in \mathbb{R}^{D} $ を返す関数として実装しています。

_activation_function.h

float *d_step(float *a, int D) {
    // a: never used
    int d; 
    float *dz_da = NULL;

    if((dz_da = (float *)malloc((D + 1) * sizeof(float))) == NULL) {
        exit(-1);
    }
    
    dz_da[0] = 0.0f;

    for(d = 1; d <= D; d++) {
        dz_da[d] = 0.0f;
    }

    return dz_da;
}

3. シグモイド関数

シグモイド関数は次のような関数でした。

h(a) = \frac{1}{1+e^{-a}}

シグモイド関数の微分は，

h'(a) = h(a)(1 - h(a))

と，シグモイド関数自体を用いて表すことができます。

\frac{\partial z_{d}}{\partial a_{d}} =  h(a_{d})(1 - h(a_{d}))

_activation_function.h

float *d_sigmoid(float *a, int D) {
    int d;
    float *z = NULL;
    float *dz_da = NULL;
    
    if((z = (float *)malloc((D + 1) * sizeof(float))) == NULL) {
        return NULL;
    }

    if((dz_da = (float *)malloc((D + 1) * sizeof(float))) == NULL) {
        exit(-1);
    }
    
    z = sigmoid(a, D);

    dz_da[0] = 0.0f;

    for(d = 1; d <= D; d++) {
        dz_da[d] = z[d] * (1.0f - z[d]);
    }

    return dz_da;
}

4. ReLU関数

ReLU関数は次のような関数でした。

h(a) = \begin{cases}
    a & \left( a \geqq 0 \right) \\
    0 & \left( \mathrm{otherwise} \right)
\end{cases}

ReLU関数を微分すると，

h'(a) = \begin{cases}
    1 & \left( a \geqq 0 \right) \\
    0 & \left( \mathrm{otherwise} \right)
\end{cases}

となります。ステップ関数と同様に， $a = 0$ での定義は，別に設けている場合があるかもしれません。

\frac{\partial z_{d}}{\partial a_{d}} =  \begin{cases}
    1 & \left( a_{d} \geqq 0 \right) \\
    0 & \left( \mathrm{otherwise} \right)
\end{cases}

_activation_function.h

float *d_ReLU(float *a, int D) {
    int d;
    float *dz_da = NULL;

    if((dz_da = (float *)malloc((D + 1) * sizeof(float))) == NULL) {
        exit(-1);
    }

    dz_da[0] = 0.0f;

    for(d = 1; d <= D; d++) {
        if(a[d] < 0.0f) {
            dz_da[d] = 0.0f;
        } else {
            dz_da[d] = 1.0f;
        }
    }

    return dz_da;
}

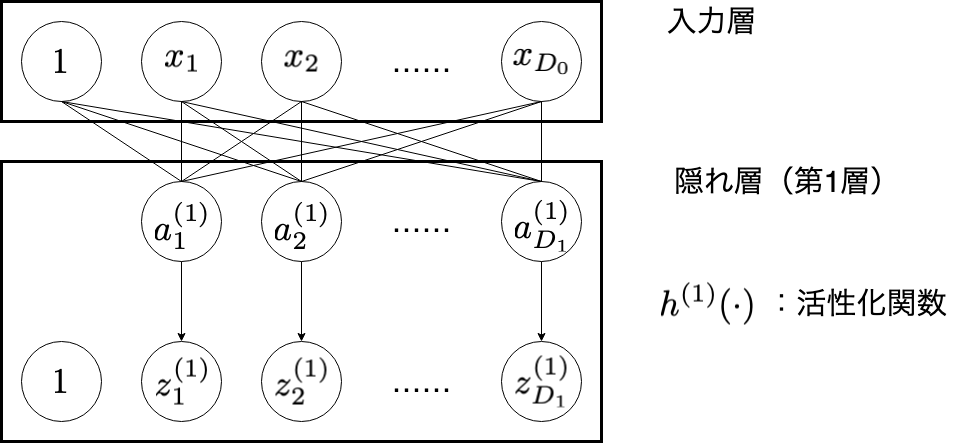
3. 入力層

入力層から隠れ層第1層の重み $w_{ij}^{(0)}$ について考えてみます...が，隠れ層での処理と同じです。

\begin{align}
\frac{\partial E}{\partial w_{ij}^{(0)}} & = \frac{\partial E}{\partial a_{j}^{(1)}}\frac{\partial a_{j}^{(1)}}{\partial w_{ij}^{(0)}} \\
&= \frac{\partial E}{\partial a_{j}^{(1)}} \cdot x_{i}
\end{align}

$\partial E / \partial a_{i}^{(0)}$ は存在しません。この $\partial E / \partial w_{ij}^{(0)}$ をもとに， $w_{ij}^{(0)}$ も更新されます。

w_{ij}^{(0)} \leftarrow w_{ij}^{(0)} - \eta \frac{\partial E}{\partial w_{ij}^{(0)}}

続き

更新履歴

2020/1/28 ゼロ除算を防ぐようにコードを修正しました。

ただし，最適解（大局的最適解）を目指しているとは限らず，図のように局所的最小解を目指してしまう可能性もある。 ↩
$\dfrac{\partial}{\partial x}f(u(x, y), t(x, y)) = \dfrac{\partial f}{\partial u}\dfrac{\partial u}{\partial x} + \dfrac{\partial f}{\partial t}\dfrac{\partial t}{\partial x}$ ↩
$\dfrac{d}{dx}(g \circ f)(x) = \dfrac{d}{dx}(g(f(x)) = g'(f(x))f'(x)$ ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up