C言語でニューラルネットワークの実装（２）〜順伝播と損失関数〜

※当初予定していたサブタイトル「〜ニューラルネットワークの学習〜」から「〜順伝播と損失関数〜」に変更しました。

前回

前回は，多層パーセプトロンの構造と活性化関数についてまとめました。多層パーセプトロンではデータの入力に対して，「重み付け和を計算する→活性化関数に通す」という処理を多層的に行うものでした。今回は，多層パーセプトロンでデータを $K$ クラスに分類する問題（多クラス分類）を解くために，学習の方法を数式を追いながらみていこうと思います。
目標：多層パーセプトロンで多クラス分類

ニューラルネットワークの学習

ニューラルネットワークの学習は，主に次の2ステップからなります。

1. 順伝播
2. 逆伝播
   順伝播は，データが入力から出力へ伝わっていくことを，逆伝播は誤差の情報が出力層から入力層の方へ伝わっていくことを意味します。今回は順伝播のみ説明し，次回，逆伝播について説明します。

順伝播

順伝播とは，値が入力層→隠れ層$1$層目→隠れ層$2$層目→...→隠れ$L$層目→出力層と値が伝わっていくことです。後の逆伝播の説明のために，具体的に式を出しながら追っていきます。

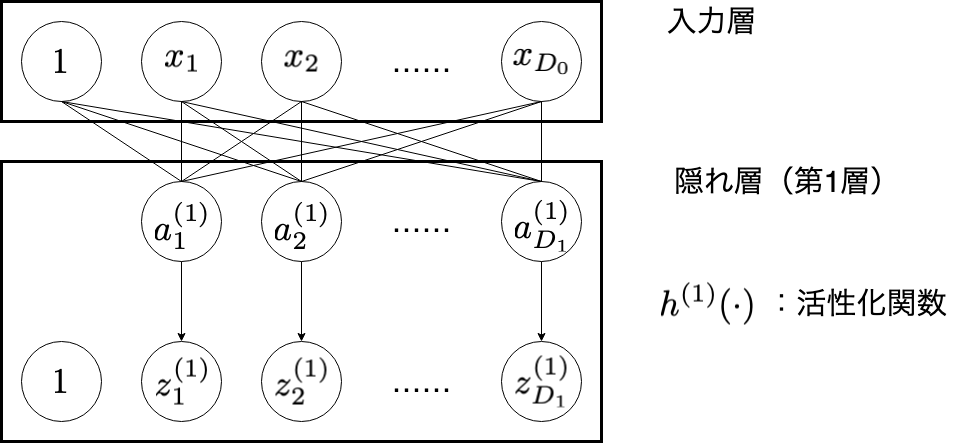
入力層（input layer）

入力層は，データを受け取る層です。これらの値を次の隠れ層の第1層目に渡します。

変数	意味
$i$	入力層のユニットのインデックス（ $i = 1, 2, \cdots , D_{0}$ ）
$j$	隠れ層（第 $1$ 層）のユニットのインデックス（ $j = 1, 2, \cdots , D_{1}$ ）
$D_{0}$	入力データの次元
$x_{i}$	入力データの各成分の値
$D_{1}$	隠れ層（第 $1$ 層）のユニットの個数
$a_{j}^{(1)}$	隠れ層（第 $1$ 層）のユニット $j$ が受け取る値
$h^{(1)}(\cdot)$	隠れ層（第 $1$ 層）の活性化関数
$z_{j}^{(1)}$	隠れ層（第 $1$ 層）のユニット $j$ に活性化関数を通した出力値

$x_{1}$，$x_{2}$，$\dots$，$x_{D_{0}}$ と並んで，定数の $1$ が並んでいます。この意味について考えたいと思います。 ある層の一つのユニットに対する入力 $a$ は次のように計算されるのでした。

a = \sum_{d=1}^{D}w_{d}z_{d} + b

このように，バイアス項 $b$ が登場します（前回を確認）。実装する際にはこの $b$ を表す変数が必要になります。この $b$ を $w_{0}$ と考えれば，次のように考えることができます。

a = \sum_{d=1}^{D} w_{d}z_{d} + w_{0} \cdot 1

ここで $z_{0} \equiv 1$ と固定すれば，

a = \sum_{d=0}^{D} w_{d}z_{d}

と書くことができます。
このように， $\boldsymbol{z}$ の次元を $D$ 次元から $D+1$ 次元へ拡張することで，実装の際に簡潔になります（ただし，図中に式で書く際は，バイアス項であることを明示するために， $w_{1}z_{1}$ 〜 $w_{D}z_{D}$ までの和と $w_{0}$ を足し合わせた表記とします）。入力層もこの例に倣い， $\boldsymbol{x}$ の次元を拡張する意味で， $1$ のユニットが一つ設置されています。

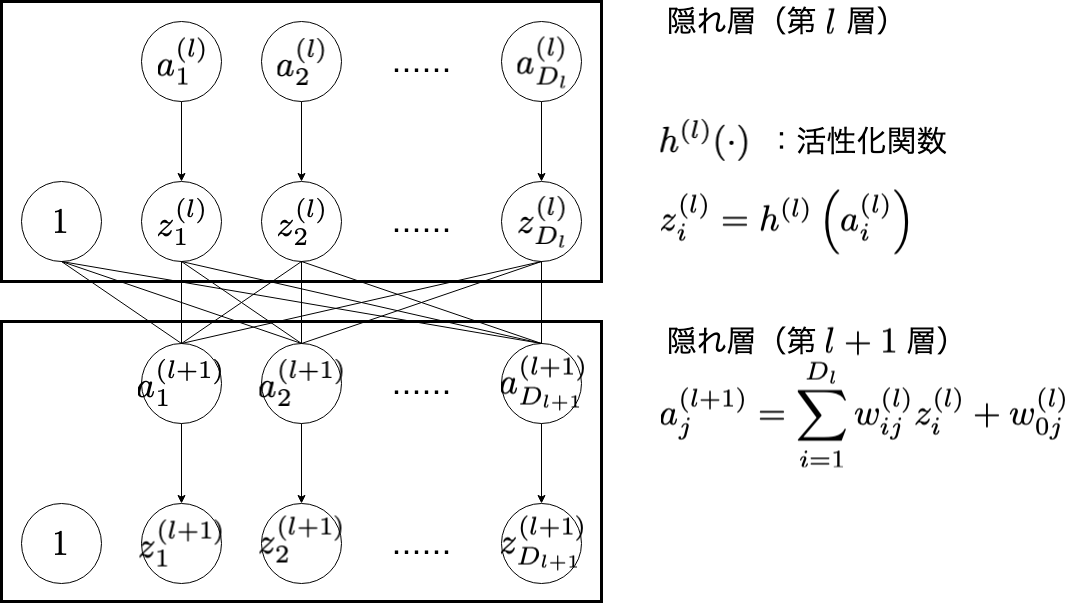
隠れ層（hidden layer）

中間層とも言います。隠れ層では，全結合と活性化を繰り返していきます。この隠れ層を何層にするかによって，ネットワークの表現力が決定します。ここでは，第 $l$ 層と第 $l+1$ 層の関係性に着目してみたいと思います。

変数	意味
$l$	隠れ層のインデックス（ $l = 1, 2, \cdots , L$ ）
$i$	隠れ層（第 $l$ 層）のユニットのインデックス（ $i = 1, 2, \cdots , D_{l}$ ）
$a_{i}^{(l)}$	隠れ層（第 $l$ 層）の入力
$h^{(l)}(\cdot)$	隠れ層（第 $l$ 層）の活性化関数
$z_{i}^{(l)}$	隠れ層（第 $l$ 層）で活性化関数を通した値
$j$	隠れ層（第 $l + 1$ 層）のユニットのインデックス（ $j = 1, 2, \cdots , D_{l+1}$ ）
$a_{j}^{(l+1)}$	隠れ層（第 $l + 1$ 層）の入力

入力層の説明でも出てきた，重み付け和をとり，バイアス項を加える操作は全結合と呼ばれます。

a_{j}^{(l+1)} = \sum_{i=1}^{D_{l}}w_{ij}^{(l)}z_{i}^{(l)} + w_{0j}^{(l)}

（ここから数行，数式の羅列が続きます。出力層の説明まで飛んでいただいて構いません。）

ここで，行列 $W^{(l)}$ とベクトル $\boldsymbol{z}^{(l)}$ ， $\boldsymbol{b}^{(l)}$ ， $\boldsymbol{a}^{(l+1)}$を次のように定義すれば，

W^{(l)} = \left( w_{ji}^{(l)} \right) \in \mathbb{R}^{D_{l+1} \times D_{l}} \\
\boldsymbol{z}^{(l)} = \left( z_{1}^{(l)}, z_{2}^{(l)}, \cdots , z_{D_{l}}^{(l)}\right)^{\top} \in \mathbb{R}^{D_{l}} \\
\boldsymbol{b}^{(l)} = \left( w_{01}^{(l)}, w_{02}^{(l)}, \cdots , w_{0D_{l+1}}^{(l)}\right)^{\top} \in \mathbb{R}^{D_{l+1}} \\
\boldsymbol{a}^{(l+1)} = \left( a_{1}^{(l+1)}, a_{2}^{(l+1)}, \cdots , a_{D_{l+1}}^{(l+1)}\right)^{\top} \in \mathbb{R}^{D_{l+1}}

全結合は次のような行列演算で並列的に表現することができます。

\boldsymbol{a}^{(l+1)} = W^{(l)}\boldsymbol{z}^{(l)} + \boldsymbol{b}^{(l)}

$\mathbb{R}^{M}$ から $\mathbb{R}^{N}$ への写像の場合，数学的にはこのような行列をかけてベクトルを足すような変換をアフィン変換（affine transformation）とも言います。ニューラルネットワークの構造の図で"Affine"などと書いてあったら，それは全結合をおこなっているという意味です。
さらに，次元をそれぞれ次のように拡張することで，

\tilde{W}^{(l)} = \left( w_{ji}^{(l)} \right) \in \mathbb{R}^{D_{l+1} \times (D_{l}+1)} \\
\tilde{\boldsymbol{z}}^{(l)} = \left( 1, z_{1}^{(l)}, z_{2}^{(l)}, \cdots , z_{D_{l}}^{(l)}\right)^{\top} \in \mathbb{R}^{D_{l} + 1}

行列をかけるだけの演算で表現できます。

\boldsymbol{a}^{(l+1)} = \tilde{W}^{(l)}\tilde{\boldsymbol{z}}^{(l)}

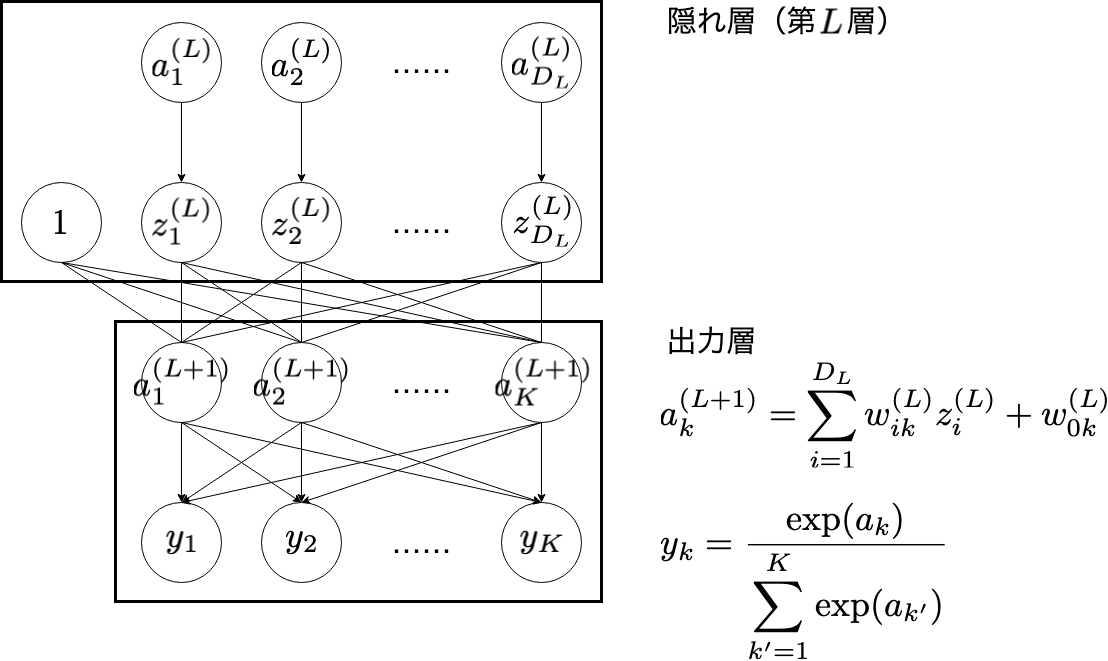
出力層

出力層では，隠れ層の最後の層（図中の第 $L$ 層）の出力を全結合で受け取り，活性化関数に通します。隠れ層と異なるのは最終的に確率を出力しなければならないというある種の制約が加わる点です。今回は， $K$ クラスの分類問題ですから，クラス $k$ （ $k=1, 2, \cdots, K$ ）の確率を出力するために，ユニット数は $K$ 個とする必要があります。また，出力が確率分布の制約を満たすようにソフトマックス関数とする必要があります。

変数	意味
$i$	隠れ層（第 $L$ 層）のユニットのインデックス（ $i = 1, 2, \cdots , D_{L}$ ）
$z_{i}^{(L)}$	隠れ層（第 $L$ 層）の出力
$k$	出力層のユニットのインデックス（ $k = 1, 2, \cdots , K$ ）
$a_{k}^{(L+1)}$	出力層の入力
$y_{k}$	出力層の出力

ちなみに，図中の $\exp(x)$ と，これまでに出てきた $e^{x}$ は同じものです。

さて，入力層に入力されたデータは「入力層→隠れ層（第 $1$ 層）→隠れ層（第 $2$ 層）→...→隠れ層（第 $L$ 層）→出力層」と流れてきました。図に登場している数式は次回（予定）の逆伝播の際に利用します。

損失関数（loss function）

損失関数は，出力層の出力 $\boldsymbol{y}$ と，正解 $\boldsymbol{t}$ のずれを計算する関数です。ニューラルネットではこの損失関数の計算結果が小さくなるように学習を進めるため，活性化関数などと同様に，目的に応じて設定する必要があります。ここでは次の2種類を説明します。

1. 平均二乗誤差
2. 交差エントロピー

コードはこちら

1. 平均二乗誤差（mean squared error）

平均二乗誤差は，回帰問題に使用される損失関数で， $\boldsymbol{y}$ と $\boldsymbol{t}$ に対して次のように定義されます。

E = \frac{1}{D} \sum_{d=1}^{D} \left( y_{d} - t_{d} \right)^{2}

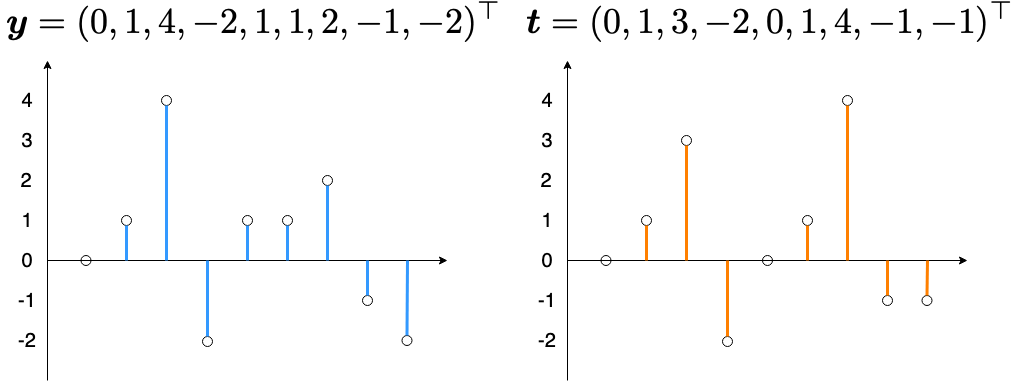
例えば，あるデータ $\boldsymbol{x}$ の入力に対して長さが $D=9$ の波形 $\boldsymbol{y}$ を推測するとします。また，このデータの正解の波形が $\boldsymbol{t}$ である場合，

平均二乗誤差は，

\begin{align}
E &= \frac{1}{9}\left[ (0 - 0)^{2} + (1 - 1)^{2} + (4 - 3)^{2} + \left\{-2 - (-2)\right\}^{2} + (1 - 0)^{2} + (1 - 1)^{2} + (2 - 4)^{2} + \left\{-1 - (-1)\right\}^{2} + (2 - 1)^{2} \right] \\
&= \frac{7}{9} \\
&\approx 0.778
\end{align}

_loss_function.h

float mean_squared_error(float *y, float *t, int D) {
    int d;
    float delta;
    float E = 0.0f;
    
    for(d = 1; d <= D; d++) {
        delta = t[d] - y[d];
        E += delta * delta;
    }
    
    return E / (float) D;
}

と計算されます。

2. 交差エントロピー（cross entropy）

交差エントロピーは，多クラス分類の際に使用される損失関数で，2つの確率分布 $\boldsymbol{p}$ と $\boldsymbol{q}$ に対して次のように定義されます。

E = - \sum_{k=1}^{K} p_{k} \log q_{k}

上の式では，対数の底を $e$ としていますが，情報理論などで単位を[bit]として扱いたい場合，底を $2$ とすることもありますが，定数倍の違い¹です。
ニューラルネットで損失関数とする場合， $p_{k}$ の部分に $t_{k}$ を， $q_{k}$ の部分に出力 $y_{k}$ を与えます。

E = - \sum_{k=1}^{K} t_{k} \log y_{k}

ただし， $t_{k}$ は，データの正解クラスが $k$ であるときに $1$ と，そうでない場合に $0$ となっています（1-of-K表現）。
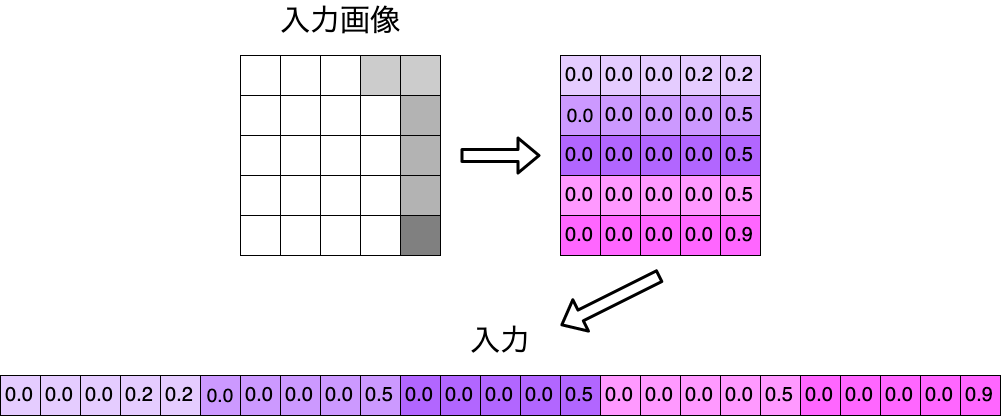
今回は， $5\times 5 = 25$ 次元のモノクロ画像のデータから，その画像が $1$ ， $2$ ， $3$ のどれであるかを推測するとします。例えば，次の画像は $1$ という文字です（だと思ってください）。これをニューラルネットワークに入力します。正解クラスが $1$ であるため， $\boldsymbol{t} = (1.0, 0.0, 0.0)^{\top}$ となります。

この入力に対して，次のような出力が得られます。

\boldsymbol{y} = (0.5, 0.4, 0.1)^{\top}

このとき，交差エントロピーは，

\begin{align}
E &= - 1.0 \log 0.5 - 0.0 \log 0.4 - 0.0 \log 0.1 \\
&\approx 0.693
\end{align}

と計算されます。次のコード上では，$\log0$による数値エラーを防ぐために，微小な値$\varepsilon$を加えています．

_loss_function.h

float EPS = 1e-12;

float cross_entropy(float *y, float *t, int K) {
    int k;
    float E = 0.0f;
    
    for(k = 1; k <= K; k++) {
        E -= t[k] * logf(y[k] + EPS);
    }
    
    return E;
}

損失

損失関数の計算結果を損失（loss）と言います。この値を小さくするように学習するということでしたが，それをどのように実現できるのかを次回まとめたいと思います。

続き

C言語でニューラルネットワークの実装（１）〜多層パーセプトロンの構造と活性化関数〜
C言語でニューラルネットワークの実装（２）〜順伝播と損失関数〜　←現在の記事
C言語でニューラルネットワークの実装（３）〜誤差逆伝播法〜
C言語でニューラルネットワークの実装（４）〜データの準備〜
C言語でニューラルネットワークの実装（５）〜モデルの構造と順伝播の実装〜
C言語でニューラルネットワークの実装（６）〜逆伝播の実装〜
C言語でニューラルネットワークの実装（７）〜オンライン学習と重みの初期値〜
C言語でニューラルネットワークの実装（８）〜ミニバッチ学習〜

更新履歴

• 2020/1/28 $\log 0$を防ぐようにコードを修正しました。

1. $\log_{2}x = \dfrac{\log x}{\log 2}$ ↩