はじめに
本記事では、AHCの過去問のネタバレを多く含みます。自力で一から試す腕試しをしたい場合は注意してください。
本記事では、線形代数の基礎知識(行列の積、逆行列、転置行列など)を要求します。
本記事はAHC典型解法をまとめたシリーズ記事の第5段です。
シリーズ全体の目的や方針は第1段を参照ください。
これまでのシリーズ記事
本記事シリーズを紹介します。
一部、他に参考となりそうな記事も紹介しています。
| 大カテゴリ | 小カテゴリ | 記事名(URL) |
|---|---|---|
| 典型手法 | モンテカルロ法 | AHC典型解法シリーズ第1弾「モンテカルロ法」 |
| 典型手法 | 焼きなまし法(山登り法含む) | AHC典型解法シリーズ第2弾「焼きなまし法」 |
| 典型手法 | ベイズ推定 | AHC典型解法シリーズ第3弾「ベイズ推定」 |
| 典型手法 | ビームサーチ (焼きなましとの合わせ技含む) | AHC典型解法シリーズ第4弾「ビームサーチ」 |
| 典型手法 | MCMC | AHC典型解法シリーズ第5弾「MCMC」 |
| 集計 | 解法まとめ | ahcまとめ(thunder) |
| 全般の進め方 | 基本的なローカルテスト | AHC初心者向け、ローカルテスタの使い方 |
MCMCの概要説明
MCMCとは
MCMCとは、「乱数を使ったシミュレーション(モンテカルロ法)」と「次の状態が現在の状態にのみ依存する過程(マルコフ連鎖)」により、複雑な確率分布からサンプルを生成する方法です。
ギブスサンプリング
MCMCの中でも、メトロポリス法やギブスサンプリングなどがありますが、今回はギブスサンプリングを説明します。
サンプリングが難しい多次元分布$p(x_1,x_2,...,x_d)$がある。
「$x_i$以外の全ての$x$を固定した状態で$x_i$をサンプリングする」を$i=1,...,d$について繰り返すと、だんだん元の多次元分布に従うサンプルに近づいていく。
簡単な問題例
推定系のAHC問題は複雑で、手法そのものの理解に集中しづらいです。
そこで、少し簡単な問題を用意しました。
未知の変数$x_1, x_2, x_3$が3つある。
観測を2回することができ、1観測ごとに、3つのうち2つの変数の名前と、その2つの変数の合計の真の値の90%~110%の値が得られる。
なお、真の値は、各値ごとにUniform(0,10)でサンプルされた値である。
各観測ごとに3変数の推定値を出力し、2回の推定の真値との誤差の二乗の平均(MSE)をなるべく小さくせよ。
1. ベイズモデルの設定
問題文に基づき、モデルを設定します。
事前分布:
$$x_i \sim \text{Uniform}(0, 10), \quad i = 1, 2, 3$$1
尤度関数:
$x_j,x_k$についての観測値は真の合計値の90%~110%の範囲の一様分布に従う:
$$y \sim \text{Uniform}(0.9(x_j + x_k), 1.1(x_j + x_k))$$
2. ギブスサンプリングのアルゴリズム
各ステップで一つの変数を他の変数を固定した条件付き分布からサンプリングします。
Step 1: 初期化
- $x_1^{(0)}, x_2^{(0)}, x_3^{(0)}$ を事前分布の期待値(5.0)で初期化2
Step 2: 反復サンプリング
各反復 $t$ において、以下を何回か繰り返す。
- $x_1^{(t+1)} \sim p(x_1 | x_2^{(t)}, x_3^{(t)}, y_1,...,y_{t,i})$
- $x_2^{(t+1)} \sim p(x_2 | x_1^{(t+1)}, x_3^{(t)}, y_1,...,y_{t,i})$
- $x_3^{(t+1)} \sim p(x_3 | x_1^{(t+1)}, x_2^{(t+1)}, y_1,...,y_{t,i})$
3. 条件付き分布の導出
変数 $x_i$ の条件付き分布は、$x_i$ を含む観測データのみに依存します。
観測 $j$ に $x_i,x_k$が含まれる場合、
$$p(x_i | x_k, y_j) \propto p(x_i) \cdot p(y_j | x_i, x_k)$$
制約条件:
- $0 \leq x_i \leq 10$ (事前分布の制約)
- $0.9(x_i + x_k) \leq y_j \leq 1.1(x_i + x_k)$ (観測制約)
これより:
$$\max\left(0, \frac{y_j}{1.1} - x_k\right) \leq x_i \leq \min\left(10, \frac{y_j}{0.9} - x_k\right)$$
よって:
$$x_i \sim \text{Uniform}(\max\left(0, \frac{y_j}{1.1} - x_k\right),\min\left(10, \frac{y_j}{0.9} - x_k\right))$$
4. 逐次更新戦略
各観測後に:
- 新しい観測データを追加
- ギブスサンプリングを実行(何回か反復)
- 最後のサンプル結果を推定値として出力
この手法により、観測データが増えるにつれて推定精度が向上し、真値に近い推定が可能になります。
具体例
ここまでの解法を具体的な真値で順を追って説明します。
真の値(未知): $x_1 = 3.0, x_2 = 6.0, x_3 = 2.0$
観測1: $(x_1, x_2)$の合計を観測
- 真の合計: $x_1 + x_2 = 3.0 + 6.0 = 9.0$
- 観測値: $y_1 = 8.5$ (真値の約94%)
ギブスサンプリング(2回反復):
各$x_i$を期待値の5.0で初期化します。
初期化: $x_1^{(0)} = 5.0, x_2^{(0)} = 5.0, x_3^{(0)} = 5.0$
反復1:
- $x_1^{(1)} \sim \text{Uniform}(\frac{8.5}{1.1} - 5.0, \frac{8.5}{0.9} - 5.0)$ → $3.5$
- $x_2^{(1)} \sim \text{Uniform}(\frac{8.5}{1.1} - 3.5, \frac{8.5}{0.9} - 3.5)$ → $5.1$
- $x_3^{(1)} \sim \text{Uniform}(0, 10)$ (制約なし)→ $4.8$
反復2:
- $x_1^{(2)} \sim \text{Uniform}(\frac{8.5}{1.1} - 5.1, \frac{8.5}{0.9} - 5.1)$ → $3.2$
- $x_2^{(2)} \sim \text{Uniform}(\frac{8.5}{1.1} - 3.2, \frac{8.5}{0.9} - 3.2)$ → $5.8$
- $x_3^{(2)} \sim \text{Uniform}(0, 10)$ → $4.2$
推定値1: $(3.2, 5.8, 4.2)$, 推定値1のMSE $1.64$
観測2: $(x_2, x_3)$の合計を観測
- 真の合計: $x_2 + x_3 = 6.0 + 2.0 = 8.0$
- 観測値: $y_2 = 8.8$ (真値の110%)
前回の推定値を初期値とする: $x_1^{(0)} = 3.2, x_2^{(0)} = 5.8, x_3^{(0)} = 4.2$
反復1:
- $x_1^{(1)} \sim \text{Uniform}(\frac{8.5}{1.1} - 5.8, \frac{8.5}{0.9} - 5.8)$ → $3.1$
- $x_2^{(1)} \sim \text{Uniform}(\max(\frac{8.5}{1.1} - 3.1, \frac{8.8}{1.1} - 4.2), \min(\frac{8.5}{0.9} - 3.1, \frac{8.8}{0.9} - 4.2))$ → $5.2$
(2回の観測で$x_1 + x_2 = 8.5$と$x_2 + x_3 = 8.8$から得られる制約を両方考慮する) - $x_3^{(1)} \sim \text{Uniform}(\frac{8.8}{1.1} - 5.2, \frac{8.8}{0.9} - 5.2)$ → $3.5$
反復2:
- $x_1^{(2)} \sim \text{Uniform}(\frac{8.5}{1.1} - 5.2, \frac{8.5}{0.9} - 5.2)$ → $3.0$
- $x_2^{(2)} \sim \text{Uniform}(\max(\frac{8.5}{1.1} - 3.0, \frac{8.8}{1.1} - 3.5), \min(\frac{8.5}{0.9} - 3.0, \frac{8.8}{0.9} - 3.5))$ → $5.5$
- $x_3^{(2)} \sim \text{Uniform}(\frac{8.8}{1.1} - 5.5, \frac{8.8}{0.9} - 5.5)$ → $3.1$
推定値2: $(3.0, 5.5, 3.1)$, 推定値2のMSE $0.49$
観測1時点の推定値と比べてもMSEが下がり、より真の分布に近いサンプリングができていることがわかります。
全体スコア: $1.063$
典型手法「MCMC」とAHC003
さて、MCMCの簡単な解説で理解を深めたところで、AHCの例題としてAHC003を扱います。
AHC003の1位のeivourさんは9通りのモデルを組み合わせる複雑な手法を使っており、これを全て解説すると膨大になってしまうため、今回はその中でもMCMCを使う部分だけピックアップして解説します。
そのため、いつものように1位越えの結果にはならず、コンテスト8位相当の結果となっています3。
今回解説する内容と別手法を組み合わせてさらなる上位スコアを目指すのも面白いかもしれません。
AHC003の問題設定
- 30*30頂点のグリッドが与えられる
- 各辺の正確な長さは与えられない
- 100回開始点と終了点が指定されるので、なるべく短い経路を出力することが目的
- 出力した経路の重みは後半ほど重い
- 出力した経路の実際の長さが±10%の誤差付きで観測できる
- 真の辺の長さは以下のルールで生成される:
- パラメータ $M \sim \text{Uniform}({1, 2})$
- パラメータ $D \sim \text{Uniform}({100,..., 2000})$
- ※$\text{Uniform}({a, ..., b})$はa以上b以下の整数から等確率で選択する分布とする
- パラメータ $B_{p,i} \sim \text{Uniform}({1000+D,..., 9000-D})$
- $B_{p,i}:$ 直線$i$の$p$番目の分割のベースの長さ
- ※問題文中は$H,V$と記載
- パラメータ $\epsilon_{i,j} \sim \text{Uniform}({-D,...,D})$
- $\epsilon_{i,j}:$ 直線$i$の$j$番目の辺に加える長さ
- ※問題文中は$\delta,\gamma$と記載
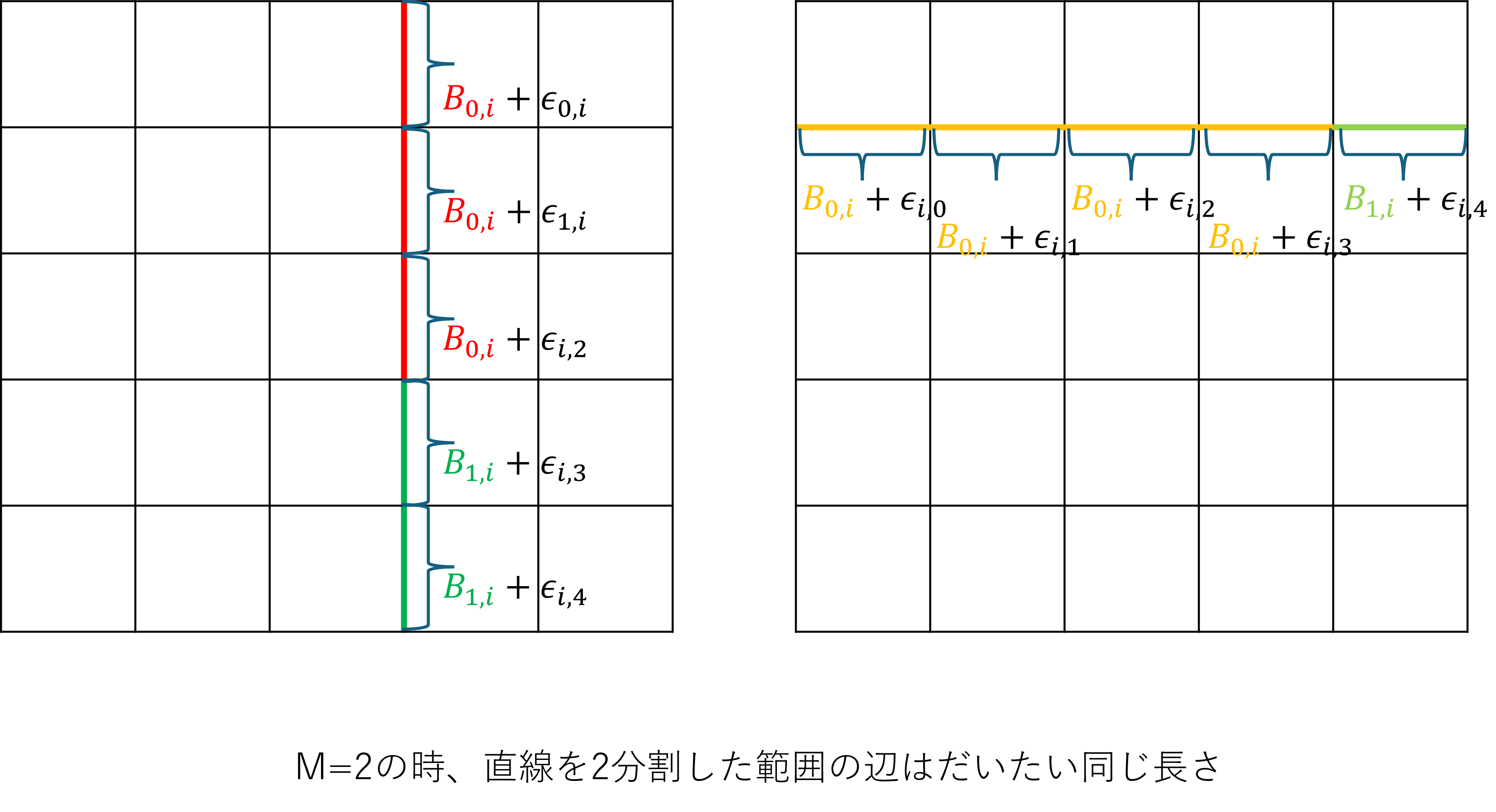
- $M=1$: 各直線$i$上の辺$j$の長さは$B_{0,i}+\epsilon_{i,j}$
- $M=2$: 各直線は2分割され、直線$i$の分割$p$の辺$j$の長さは$B_{p,i}+\epsilon_{i,j}$
解法
解法概要
本問題では、Mの値次第で構造が大きく変わる点や、一様分布に従う確率変数が再帰構造になっている点から、そのままでは事後分布を推定することが難しいです。
先述の通り、サンプリングが難しい場合はギブスサンプリングが選択肢になりますが、推定対象となる辺の数が$29 \times 30 \times 2 =1740$ もあり、制限時間内の推定は難しそうです。
そのため、以下のように問題を単純化します。
- 常にM=2と考える(真のMが1の場合は観測がもったいないが、とりあえず推定できる) 4
- 制限時間内に推定するために少ない変数で構成したモデルで近似する
- セグメント単位でギブスサンプリングする
近似モデル
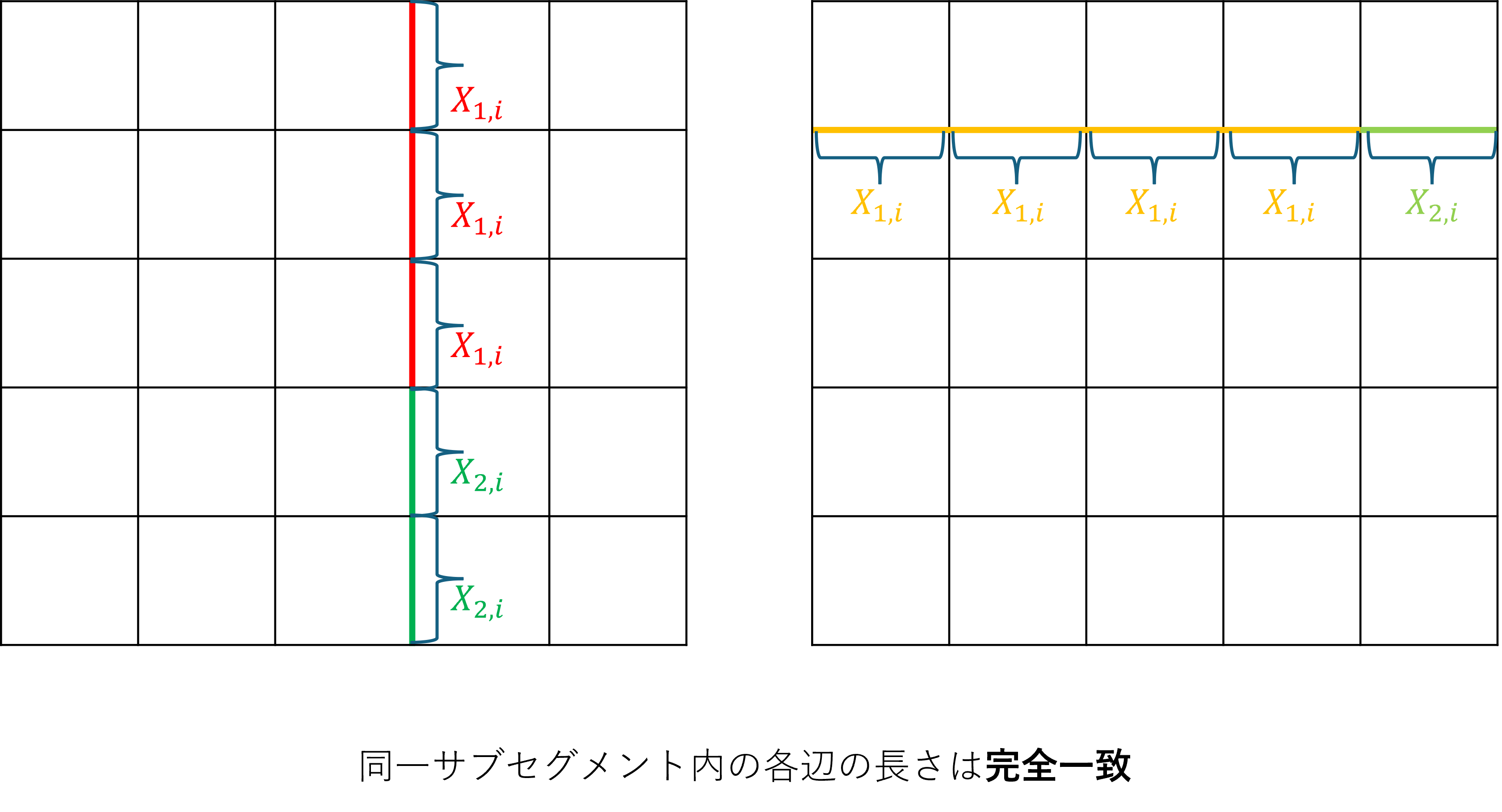
説明のため、今後は直線のことをセグメント、各セグメントを2分割した範囲をサブセグメントと呼びます。
各サブセグメントは近い長さであることから、各サブセグメントごとに統一した確率分布として近似します。
問題文ままの分布と異なる形で分布を仮定することになるのですが、今回は事後分布5を推定しやすくするために、共役事前分布を利用します。
一般に、尤度6に対し、事後分布のパラメータを簡単に特定できる事前分布を共役事前分布と呼びます。尤度が正規分布で、事前分布が正規分布の場合、事後分布も正規分布になるため、今回はこれを利用します。
- セグメント$i$の分割点:$z_i \sim \text{Uniform}({1,...,28})$ ※問題文中の$y$に相当
- セグメント$i$の左側(上側)1辺あたりの長さ : $X_{1,i} \sim \mathcal{N}(E[B],V[B])$ 7
- セグメント$i$の右側(下側)1辺あたりの長さ : $X_{2,i} \sim \mathcal{N}(E[B],V[B])$
- $D \sim \text{Uniform}(100,2000)$ ※問題文は離散値だが、連続値として扱う
- $B_{p,i} \sim \text{Uniform}(1000+D,9000-D)$ ※問題文の$H,V$相当、連続値として扱う
- サブセグメント内の辺は全て同じ長さだと仮定する ※本来は「ほぼ同じ」だが、変数を減らすために「同じ」と仮定
- $t$回目に観測されたセグメント$i$を通る経路の長さ $y_{t,i} \sim \mathcal{N}(l_{t,i} X_{1,i} + r_{t,i} X_{2,i}, \sigma_t^2)$
- $\sigma_t^2$ : 観測とモデル近似による誤差
- $l_{t,i}$ : その経路で通ったセグメントの左側(上側)サブセグメントの辺数
- $r_{t,i}$ : その経路で通ったセグメントの右側(下側)サブセグメントの辺数
事前分布
$X_{1,i},X_{2,i}$について、以下の仮定をしているため、$E[B],V[B]$を求めれば事前分布の形がわかります。
\begin{align}
X_{1,i} &\sim \mathcal{N}(E[B],V[B])\\
X_{2,i} &\sim \mathcal{N}(E[B],V[B])\\
D &\sim \text{Uniform}(100,2000)\\
B_{p,i} &\sim \text{Uniform}(1000+D,9000-D)
\end{align}
全期待値の法則より、以下が求まります。8
$$E[B]=E[E[B|D]]=\frac{(1000+D)+(9000-D)}{2}=5000$$
全分散の法則より、9
$$V[B] = E[V[B|D]] + V[E[B|D]]$$
$E[B|D] = 5000$ (定数) なので $V[E[B|D]] = 0$
条件付き分散:
$$V[B|D] = \frac{(8000-2D)^2}{12}$$
$E[D] = 1050$, $E[D^2] = \frac{100^2 + 100 \times 2000 + 2000^2}{3} \approx 1,403,333.333$ を用いて
$$V[B] = E[V[B|D]] = \frac{E[(8000-2D)^2]}{12} \approx \frac{36,013,333.332}{12} = 3,001,111.111$$
よって、
\begin{align}
X_{1,i} \sim \mathcal{N}(5000, 3,001,111.111)\\
X_{2,i} \sim \mathcal{N}(5000, 3,001,111.111)
\end{align}
観測モデル
ジャッジシステムから入力される経路は複数のセグメントをまたがりますが、パラメータ更新はセグメント毎に独立に行います。
先述の通り、仮定した観測モデルを以下の通りです。
平均についてはセグメント$i$を通った部分の長さの予測値で、分散については詳細を説明します。
セグメント$i$についての観測モデル:
$$y_{t,i} \sim \mathcal{N}(l_{t,i} X_{1,i} + r_{t,i} X_{2,i}, \sigma_t^2)$$
- $l_{t,i}$: $t$回目の経路でセグメント$i$の左側を通った辺数
- $r_{t,i}$: $t$回目の経路でセグメント$i$の右側を通った辺数
- $\sigma_t^2$: 経路全体から計算される観測誤差の分散
分散の計算
今回近似したモデルには2つの異なる誤差源があります。
1. 問題文に記載の誤差:
- ジャッジシステムが返す値には真値の±10%の誤差がある
- 観測値 = 真値 × $r$, $r \sim \text{Uniform}(0.9, 1.1)$
- 観測モデルでは真値に比例した分散を持つ
$$\frac{(0.1y_{t})^2}{3}$$
ここで、$y_t$は経路全体の観測とします。
2. モデル近似による誤差:
- 今回の近似モデルは各辺が$B_{p,i}$で、各サブセグメントで一定だが、真値は$B_{p,i}+\epsilon_{i,j}$であり、辺毎に発生する誤差$\epsilon_{i,j}$を考慮する必要がある。
- $\epsilon_{i,j} \sim \text{Uniform}(-D,D)$
- 全分散の法則より、
\begin{align}
V[\epsilon_{i,j}] &= E[V[\epsilon_{i,j}|D]]+V[E[\epsilon_{i,j}|D]] \\
&= E[\frac{D^2}{3}]+V[0]\\
&\approx 467,777.778
\end{align}
3. 観測の分散
モデル近似による誤差は辺ごとに発生するため、観測ルートの辺数を$len$としたとき、観測の分散は以下の式となる
$$V[\epsilon_{i,j}] \times len$$
ただし、問題文の相対誤差(±10%)は真値に比例するため、実際の観測モデルでは以下のようになる:
観測モデルの計算結果:
$$y_{t,i} \sim \mathcal{N}\left(l_{t,i} X_{1,i} + r_{t,i} X_{2,i}, \frac{(0.1y_{t})^2}{3} + 467,777.778 len_t\right)$$
近似モデルの目標
さて、ここまでモデルを近似する方針を解説しました。
この近似モデルのパラメータを全て推定できれば、最短経路を求めることが可能になります。
つまり、観測データ$ y_{t,i}, \ldots, y_{t,i}$ が得られた時の、全180パラメータの事後分布を求めることが目標となります。
$$
\text{全パラメータ}: z_0,X_{1,0},X_{2,0},z_1,X_{1,1},X_{2,1},\ldots,z_{59},X_{1,59},X_{2,59}
$$
ギブスサンプリング
セグメント単位での固定:
今回、セグメント単位でギブスサンプリングを適用します。
まず、各パラメータを事前分布の期待値で初期化します。
$$(14,5000,5000),(14,5000,5000),\ldots,(14,5000,5000)$$
経路の長さ$y_1$を観測した後、この情報を元に各パラメータをサンプリングしなおします。
この時、セグメント$i$を更新する時はセグメント$i$以外の全てのセグメントのパラメータを固定し、観測データに基づいてセグメント$i$のパラメータのみを事後分布からサンプリングします。
セグメント$0$の更新時はセグメント$0$以外を固定
$$(z_0,X_{1,0},X_{2,0}),(14,5000,5000),\ldots,(14,5000,5000)$$
セグメント$0$を事後分布でサンプリングして、
$$(10,4800,6100),(14,5000,5000),\ldots,(14,5000,5000)$$
セグメント$1$の更新時はセグメント$1$以外を固定
$$(10,4800,6100),(z_1,X_{1,1},X_{2,1}),\ldots,(14,5000,5000)$$
セグメント$1$を事後分布でサンプリングして、
$$(10,4800,6100),(12,5300,5100),\ldots,(14,5000,5000)$$
これをセグメント$59$まで繰り返せば、全パラメータが事後分布によってサンプリングした値になるため、初期値よりも観測に沿った値に近づいていきます。
1セグメントの更新内でのギブスサンプリング:
セグメント$i$以外の全てのパラメータを固定しても、セグメント$i$の中でも一様分布に従う$z_i$と正規分布に従う$X_{1,i},X_{2,i}$を同時にサンプリングするのは難しいです。
ここで、$z_i$も固定することで、変数は$X_{1,i},X_{2,i}$だけになり、2変数正規分布となります。
正規分布であれば共役事前分布となるため、解析的に周辺尤度や事後分布が求まります。
${1,2,\dots,27}$ 全ての区切り目$z_i$で$X_{1,i},X_{2,i}$を周辺化し、$z_i$に関する尤度を求めます。
$z_i$の事前分布は一様分布なので正規化した尤度がそのまま事後分布として扱えます。
求めた事後分布でサンプリングした$z_i$を固定できるので、$X_{1,i},X_{2,i}$も事後分布でサンプリングできます。
サンプリング回数:
- このプロセスを複数回繰り返すことで、各パラメータがより精度の高い事後分布からサンプリングされます
- 新しい観測$y_2, y_3, \ldots$が得られるたびに、この過程を繰り返してパラメータを更新していきます
全体の流れ:
まとめると、以下のギブスサンプリングの流れで推定を進めます。
- 各観測$y_t$が得られるたび
- 指定した回数だけ以下をループ
- 各セグメント$i$について
- ステップ1: $z_i$の更新
- 各分割点候補$z_i \in {0,1,\ldots,27}$について:
- $z_i$を固定した時の$X_{1,i},X_{2,i}$の事後分布パラメータ計算
- $z_i$の周辺尤度計算
- 周辺尤度に基づく確率で$z_i$をサンプリング
- 各分割点候補$z_i \in {0,1,\ldots,27}$について:
- ステップ2: $X_{1,i}, X_{2,i}$の更新
- サンプリングした$z_i$を固定
- ステップ1で計算した事後分布パラメータから$X_{1,i}, X_{2,i}$をサンプリング
- ステップ1: $z_i$の更新
- 各セグメント$i$について
- 指定した回数だけ以下をループ
分割点を固定した時のXの事後分布パラメータ計算
ベイズ推定
1つのセグメント$i$について説明します。
$n$回目の観測後の$X_{1,i},X_{2,i}$の事後分布$p(X_{1,i},X_{2,i}| y_{1,i}, \ldots, y_{n,i}, z_i)$を計算するため、ベイズの定理を利用します。
$$p(X_{1,i},X_{2,i}| y_{1,i}, \ldots, y_{n,i}, z_i) \propto p(y_{1,i}, \ldots, y_{n,i} | X_{1,i},X_{2,i}, z_i) \times p(X_{1,i},X_{2,i})$$ 10
各観測は独立に発生するため、尤度は積の形で表現できます。
$$p(y_{1,i}, \ldots, y_{n,i} | X_{1,i},X_{2,i}, z_i) = \prod_{t=1}^n p(y_{t,i} | X_{1,i},X_{2,i}, z_i)$$ 11
上記ベイズの定理の式にあてはめ、
$$p(X_{1,i},X_{2,i} | y_{1,i}, \ldots, y_{n,i}, z_i) = p(X_{1,i},X_{2,i}) \times \prod_{t=1}^n p(y_{t,i} | X_{1,i},X_{2,i}, z_i)\times \text{定数}$$
オーバーフロー対策で積を和に変換するため、対数を取ります。
$$\log p(X_{1,i},X_{2,i} | y_{1,i}, \ldots, y_{n,i}, z_i) = \log p(X_{1,i},X_{2,i}) + \sum_{t=1}^n \log p(y_{t,i} | X_{1,i},X_{2,i}, z_i) + \text{定数}$$
パラメータ更新のための式変形
$\mathbf{X}=(X_1,X_2)$とすると、2次元正規分布の確率密度関数$p(\mathbf{X})$は以下の式で表せます。
$$
p(\mathbf{X}) = \frac{\sqrt{|\boldsymbol{\Lambda}|}}{2\pi }
\exp\left( -\tfrac{1}{2} (\mathbf{X}-\boldsymbol{\mu})^T \boldsymbol{\Lambda} (\mathbf{X}-\boldsymbol{\mu}) \right)
$$
- $\boldsymbol{\Lambda}$:精度行列(分散の逆行列)
- $\boldsymbol{\mu}$:平均ベクトル
これを対数を取って展開します。
\begin{align}
\log p(\mathbf{X}) &= \log{\frac{\sqrt{|\boldsymbol{\Lambda}|}}{2\pi }} -\tfrac{1}{2} (\mathbf{X}-\boldsymbol{\mu})^T \boldsymbol{\Lambda} (\mathbf{X}-\boldsymbol{\mu}) \\
&= \log{\frac{\sqrt{|\boldsymbol{\Lambda}|}}{2\pi }} -\frac{1}{2} \mathbf{X}^T \boldsymbol{\Lambda} \mathbf{X} + \mathbf{X}^T \boldsymbol{\Lambda}\boldsymbol{\mu} -\frac{1}{2} \boldsymbol{\mu} ^T \boldsymbol{\Lambda} \boldsymbol{\mu}\\
&= -\frac{1}{2} \mathbf{X}^T \boldsymbol{\Lambda} \mathbf{X} + \mathbf{X}^T \boldsymbol{\Lambda}\boldsymbol{\mu} +\left(\log{\frac{\sqrt{|\boldsymbol{\Lambda}|}}{2\pi }} -\frac{1}{2} \boldsymbol{\mu} ^T \boldsymbol{\Lambda} \boldsymbol{\mu}\right)
\end{align}
$\mathbf{X}$の次数で整理すると、全ての項が以下の形に統一される
$$
\log p(\mathbf{X}) =-\frac{1}{2} \mathbf{X}^T \boldsymbol{A} \mathbf{X} + \mathbf{X}^T \boldsymbol{b} + \boldsymbol{c}
$$
事前分布と各観測の尤度をこの形で表現することで、単純に係数を足し合わせることでパラメータを更新可能になります。
先ほどベイズの定理で導いた対数事後尤度の式に代入すると、
\log p(X_{1,i},X_{2,i} | y_{1,i}, \ldots, y_{t,i}, z_i) = -\frac{1}{2} \mathbf{X}^T \boldsymbol{A_{0,i}} \mathbf{X} + \mathbf{X}^T \boldsymbol{b_{0,i}} + \boldsymbol{c_{0,i}} + \sum_{t=1}^n \left( -\frac{1}{2} \mathbf{X}^T \boldsymbol{A}_{t,i} \mathbf{X} + \mathbf{X}^T \boldsymbol{b}_{t,i} + \boldsymbol{c}_{t,i} \right)+ \text{定数}
次数で整理して
-\frac{1}{2} \mathbf{X}^T \underbrace{\left(\boldsymbol{A_{0,i}} +\sum_{t=1}^n \boldsymbol{A}_{t,i} \right)}_{\boldsymbol{A}_n} \mathbf{X} + \mathbf{X}^T \underbrace{\left(\boldsymbol{b_{0,i}} +\sum_{t=1}^n \boldsymbol{b}_{t,i} \right)}_{\boldsymbol{b}_n} +\underbrace{\left(\boldsymbol{c_0}+\boldsymbol{c_t}\right)}_{\boldsymbol{c}_n}+ \text{定数}
事後分布のパラメータ$\boldsymbol{A_{n,i}},\boldsymbol{b_{n,i}},\boldsymbol{c_{n,i}}$を計算するため、$\boldsymbol{A_{0,i}},\boldsymbol{b_{0_i}},\boldsymbol{c_{0,i}},\boldsymbol{A_{t,i}},\boldsymbol{b_{t,i}},\boldsymbol{c_{t,i}}$を求めます。
事前分布についての計算
仮定した事前分布は2次形式で表すと以下の通りです。
\begin{align}
\mathbf{X} \sim \mathcal{N}\left(\begin{pmatrix} \mu_1 \\ \mu_2 \end{pmatrix}, \begin{pmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_2^2 \end{pmatrix}\right)
\end{align}
$\mu_1=\mu_2=5000$
$\sigma_1^2=\sigma_2^2=3,001,111.111$
\begin{align}
\boldsymbol{A_{0,i}} &= \Sigma_0^{-1} \\
&= \begin{pmatrix} \sigma_1^2 & 0 \\ 0 & \sigma_2^2 \end{pmatrix}^{-1} \\
&= \begin{pmatrix} \frac{1}{\sigma_1^2} & 0 \\ 0 & \frac{1}{\sigma_2^2} \end{pmatrix} \\
&= \begin{pmatrix} \frac{1}{3,001,111.111} & 0 \\ 0 & \frac{1}{3,001,111.111} \end{pmatrix}
\end{align}
\begin{align}
\boldsymbol{b_{0,i}} &= \boldsymbol{A_{0,i}} \boldsymbol{\mu} \\
&= \begin{pmatrix} \frac{1}{\sigma_1^2} & 0 \\ 0 & \frac{1}{\sigma_2^2} \end{pmatrix} \begin{pmatrix} \mu_1 \\ \mu_2 \end{pmatrix} \\
&= \begin{pmatrix} \frac{\mu_1}{\sigma_1^2} \\ \frac{\mu_2}{\sigma_2^2} \end{pmatrix} \\
&= \begin{pmatrix} \frac{5000}{3,001,111.111} \\ \frac{5000}{3,001,111.111} \end{pmatrix}
\end{align}
尤度についての計算
$\log p(y_{t,i} | X_{1,i},X_{2,i}, z_i)$についても同様にパラメータを計算します。
観測はセグメントをまたいだ全経路$y_t$しか取得できないため、セグメント$i$だけにしぼった情報$y_{t,i}$を概算する必要があります。
ギブスサンプリングの過程でセグメント$j(\neq i)$の経路は$X_{1,j},X_{2,j},z_j$を固定しているので、通った経路の長さを予測できます。
そのため、セグメント$i$の観測は、全経路の観測からセグメント$i$以外の予測長を引いたもので概算できます。
$$y_{t,i}=y_t-\sum_{\substack{j=1 \\ j\neq i}}^n \left(l_{t,j} X_{1,j} + r_{t,j} X_{2,j}\right)$$
観測 $y_{t,i} \sim \mathcal{N}(l_{t,i} X_{1,i} + r_{t,i} X_{2,i}, \sigma_t^2)$ の確率密度は正規分布の一般的な式で計算できます。
$$\log p(y_{t,i} | X_{1,i}, X_{2,i}) = -\frac{1}{2\sigma_t^2}(y_{t,i} - l_{t,i} X_{1,i} - r_{t,i} X_{2,i})^2 + \text{定数}$$
これを展開して、$\boldsymbol{A_{t,i}},\boldsymbol{b_{t,i}},\boldsymbol{c_{t,i}}$に対応させます。
\begin{align}
\log p(y_{t,i} | X_{1,i}, X_{2,i}) &= -\frac{1}{2\sigma_t^2}(y_{t,i} - l_{t,i} X_{1,i} - r_{t,i} X_{2,i})^2 + \text{定数}\\
&=-\frac{1}{2\sigma_t^2}\left(y_{t,i}^2 - 2y_{t,i}(l_{t,i} X_{1,i} + r_{t,i} X_{2,i}) + (l_{t,i} X_{1,i} + r_{t,i} X_{2,i})^2\right)+ \text{定数}\\
&=-\frac{1}{2\sigma_t^2}\left(y_{t,i}^2 - 2y_{t,i}(l_{t,i} X_{1,i} + r_{t,i} X_{2,i}) + l_{t,i}^2 X_{1,i}^2 + 2l_{t,i} r_{t,i} X_{1,i} X_{2,i} + r_{t,i}^2 X_{2,i}^2\right)+ \text{定数}\\
&=-\frac{1}{2\sigma_t^2}\left(y_{t,i}^2 - 2y_{t,i} \begin{pmatrix}l_{t,i} & r_{t,i}\end{pmatrix} \begin{pmatrix}X_{1,i} \\ X_{2,i}\end{pmatrix} + \begin{pmatrix}X_{1,i} & X_{2,i}\end{pmatrix} \begin{pmatrix}l_{t,i}^2 & l_{t,i} r_{t,i} \\ l_{t,i} r_{t,i} & r_{t,i}^2\end{pmatrix} \begin{pmatrix}X_{1,i} \\ X_{2,i}\end{pmatrix}\right)+ \text{定数}\\
&=-\frac{1}{2\sigma_t^2}\begin{pmatrix}X_{1,i} & X_{2,i}\end{pmatrix} \begin{pmatrix}l_{t,i}^2 & l_{t,i} r_{t,i} \\ l_{t,i} r_{t,i} & r_{t,i}^2\end{pmatrix} \begin{pmatrix}X_{1,i} \\ X_{2,i}\end{pmatrix}+\frac{y_{t,i}}{\sigma_t^2}\begin{pmatrix}l_{t,i} & r_{t,i}\end{pmatrix} \begin{pmatrix}X_{1,i} \\ X_{2,i}\end{pmatrix}-\frac{y_{t,i}^2}{2\sigma_t^2}+\text{定数}\\
&=-\frac{1}{2}\mathbf{X}^T \underbrace{\frac{1}{\sigma_t^2}\begin{pmatrix}l_{t,i}^2 & l_{t,i} r_{t,i} \\ l_{t,i} r_{t,i} & r_{t,i}^2\end{pmatrix}}_{\boldsymbol{A}_{t,i}} \mathbf{X}+\mathbf{X}^T\underbrace{\frac{y_{t,i}}{\sigma_t^2}\begin{pmatrix}l_{t,i} \\ r_{t,i}\end{pmatrix}}_{\boldsymbol{b}_{t,i}} +\underbrace{-\frac{y_{t,i}^2}{2\sigma_t^2}}_{\boldsymbol{c}_{t,i}}+\text{定数}
\end{align}
$\boldsymbol{A_{0,i}},\boldsymbol{A_{t,i}},\boldsymbol{b_{0,i}},\boldsymbol{b_{t,i}}$が求まったので、これで事後分布の形がわかります。
分割点の周辺尤度計算とサンプリング
各分割点候補$z_i$の周辺尤度は以下の式で計算できます。
$$p(y_{1,i}, \ldots, y_{n,i} | z_i) = \int \int p(y_{1,i}, \ldots, y_{n,i} | X_{1,i}, X_{2,i}, z_i) \times p(X_{1,i}, X_{2,i}) , dX_{1,i} , dX_{2,i}$$
この積分の中身は、先ほど変形した事後分布の指数部分と同じ形になります。
$$
p(y_{1,i}, \ldots, y_{n,i}| z_i) = \int \exp!\left( -\tfrac12 \mathbf{X}^T \boldsymbol{A_{n,i}}\mathbf{X}+ \mathbf{X}^T \boldsymbol{b_{n,i}}+ c_{n,i} \right), d\mathbf{X}
$$
一般に、$d$次元の$\mathbf{X}$について以下の式が知られています。
$$
\int_{\mathbb{R}^d}
\exp\left(
-\frac{1}{2} \mathbf{X}^T \mathbf{A} \mathbf{X} + \mathbf{b}^T \mathbf{X}+c
\right),d\mathbf{X}
= (2\pi)^{d/2},|\mathbf{A}|^{-1/2},
\exp\left(\frac{1}{2} \mathbf{b}^T \mathbf{A}^{-1}\mathbf{b}+c\right)
$$
2次元の式である上記に当てはめます。
$$
p(y_{1,i}, \ldots, y_{n,i}| z_i) = 2\pi,|\boldsymbol{A_{n,i}}|^{-1/2},
\exp\left(\frac{1}{2} \boldsymbol{b_{n,i}}^T \boldsymbol{A_{n,i}}^{-1}\boldsymbol{b_{n,i}}+c_{n,i}\right)
$$
対数をとると以下の式になります。
\begin{align}
\log p(y_{1,i}, \ldots, y_{n,i}| z_i) = \log 2\pi-\frac{1}{2}\log \,|\boldsymbol{A_{n,i}}|\,+
\frac{1}{2} \boldsymbol{b_{n,i}}^T \boldsymbol{A_{n,i}}^{-1}\boldsymbol{b_{n,i}}+c_{n,i}
\end{align}
実際の実装では、相対的な比較のみが必要なため、定数項$\log(2\pi)$は省略されることが多いです。
この式で全ての分割点候補$z_i \in {0, 1, \ldots, 27}$の周辺尤度を計算し、その確率に基づいて$z_i$をサンプリングします。
具体的なサンプリング手順:
-
周辺尤度の計算: 各$z_i \in {0, 1, \ldots, 27}$について$\log p(y_{1,i}, \ldots, y_{n,i} | z_i)$を計算
-
数値安定化: 最大値で正規化
$$\log w_k = \log p(y_{1,i}, \ldots, y_{n,i} | z_i = k) - \max_{k'} \log p(y_{1,i}, \ldots, y_{n,i} | z_i = k')$$ -
確率の計算: 指数関数を適用して確率に変換
$$w_k = \exp(\log w_k), \quad p_k = \frac{w_k}{\sum_{k'=0}^{27} w_{k'}}$$ -
離散サンプリング: 確率${p_0, p_1, \ldots, p_{27}}$に基づいて$z_i$を1つ選択
この手順により、周辺尤度が高い分割点ほど選ばれやすくなり、観測データに適した$z_i$がサンプリングされます。
実装上は、C++ではstd::discrete_distributionを用いて、各分割点の周辺尤度を重みとした離散サンプリングが可能です。
Xの更新
$z_i$がサンプリングできたので、あとは$X_{1,i}, X_{2,i}$をサンプリングできれば、全てのパラメータを推定できます。
まず、事後分布のパラメータ$\boldsymbol{A_{n,i}},\boldsymbol{b_{n,i}}$より、共分散行列$\boldsymbol{\Sigma_{n,i}}$と平均ベクトル$\boldsymbol{\mu_{n,i}}$を求めます。
\begin{align}
\boldsymbol{\Sigma}_{n,i}=\boldsymbol{A}_{n,i}^{-1}\\
\boldsymbol{\mu}_{n,i}=\boldsymbol{\Sigma}_{n,i}\boldsymbol{b}_{n,i}^T
\end{align}
標準正規分布であればstd::normal_distributionなどで簡単にサンプリング可能ですが、今回のように共分散を持つ正規分布のサンプリングは直接的なサンプリングが難しいため、コレスキー分解を活用することでサンプリングできます。
$\boldsymbol{\Sigma}_{n,i} = \mathbf{L}\mathbf{L}^T$となる$\mathbf{L}$を求めます。
すると、以下のようにサンプリングが可能です。
$$
\mathbf{X}=\mathbf{L}\boldsymbol{\eta}+\boldsymbol{\mu}_{n,i}\
\boldsymbol{\eta} \sim \mathcal{N}(\mathbf{0},\mathbf{I})
$$
経路の出力
ここまで、ギブスサンプリングによって各辺の長さがサンプリングできました。
この問題では短い経路を出力することが目的なので、経路の出力方法を考えます。
推定した各辺の長さをそのまま使えばdijkstra法で最適解が求まるのですが、これだと推定のための情報があまり集まらず、推定精度が悪いままで経路探索をし続けることになります。
そこで、探索と活用のバランスをとりながら出力する経路を決めるとよいです。
$n$回の観測を追えた時点で、以下のような式で各辺のコストを決め、このコストが最小となるようにdjkstra法で経路を決めます。
\begin{align}
\text{LCB}&=\underbrace{\mu_{e,n}}_{活用}-\underbrace{\gamma_n\sqrt{\sigma_{e,n}^2}}_{探索}\\
\mu_{e,n}& : \text{辺}e\text{について今までサンプリングした値の平均値}\\
\sigma_{e,n}^2& : \text{辺}e\text{について今までサンプリングした値の分散}\\
\gamma_n & : \text{探索のバランスをとるためのスケジュールパラメータ}
\end{align}
これはLower Confidence Boundと呼ばれる手法で、多腕バンディット問題でよく使われる探索と活用のバランシング手法です。
効果:
- 分散が大きい(不確実性が高い)辺ほど、LCBが小さくなり選ばれやすくなる
- 十分に観測された辺は平均値に近いコストで評価される
- 時間とともに$\gamma_n$を減少させることで、徐々に活用重視に移行
スケジューリング
今回のアルゴリズムでは、「各観測で何回サンプリングしなおすか」と「LCBの探索の重み」を1000回の観測ごとに調整するとよいです。
各観測で何回サンプリングしなおすか
観測の初期では推定を早く収束させたいため、たくさんサンプリングしておき、収束に近い後半ではサンプリング回数を減らしていきます。
具体的には、$n$回目の観測($n = 0, 1, \ldots, 999$)で以下の回数だけサンプリングを行います:
$$\text{サンプリング回数} = 20^{1-n/1000} \times 4^{n/1000}$$
サンプリング回数を20回から指数的に下げ、最終的に4回にするようにしています。
eivourさんは初回の200観測までサンプリング回数10、それ以降は2回としていましたが、今回はeivourさんが使っていた他のモデルに時間を割かない分、多めにしています。
LCBの探索の重み
先述の通り、LCBの探索の重みは時間と共に減らすとよいです。
今回は以下のスケジュールで実装しました。
$$\gamma_n=1.5\left(1-\frac{n}{1000}\right)^2$$
最後に
この記事では、MCMCを用いた解法を紹介しました。
スコアは当日相当でざっくり8位ぐらいです。
本当は1位のeivourさんの手法を参考に作っているのですが、今回はMCMCの解説に特化するため、eivourさんの手法のコアとなる1740次元の正規分布モデルを実装していません。
eivourさんの実装では本来$M,D$のパラメータが特定の範囲だと推定された場合のみMCMCを使う方針で、$M=2$の形状に合わせてMCMCモデルを仮定していることにも意味があります。
また、eivourさんが行っていたSIMDによる高速化も今回は除外しています。
ここからさらに上位スコアに近づくためにはどのような改善が必要か考えてみるのもおもしろいかもしれません。
| ユーザ | スコア | 順位(コンテスト時、システス前の簡易ジャッジ概算) |
|---|---|---|
| eivour | 97448033028 | 1 |
| yosss | 97354398934 | 2 |
| Komaki | 97341260792 | 3 |
| primenumber | 97300905660 | 4 |
| toame | 97299034675 | 5 |
| saharan | 97291365214 | 6 |
| gasin | 97223856984 | 7 |
| 筆者の提出 | 97170039790 | 8位相当 提出リンク |
| tomerun | 97156790300 | 8 |
最後にサンプルコードを掲載します。
行列演算部分だけファイルを分割していますが、thunder/ahc003_mcmc.cppだけ見れば概ねの動きは理解できると思います。
https://github.com/thun-c/ahc003_sample/
-
$x \sim \text{Uniform}(a, b) は、xがa以上b以下の一様分布に従う、つまりこの区間の全ての値が等しい確率密度を持つことを意味します。$ ↩
-
$x_i^{(t)}$は、変数$t$回目の観測後の$x_i$を示す。$t=0$は観測前の初期値 ↩
-
AHC003では延長戦順位表がないため、全ての提出から 2021-05-30(日) 20:00以前のスコアを降順に並べ、ユニークな各プレイヤーの最大スコアと比較して何番目だったかを見ることで概算できます。システムテストのシードも公開されているので、これを利用すればローカルでテストすることも可能ですが、AtCoderと完全に同じ計算環境が用意できない点と、筆者の環境では上位プレイヤーの一部のコードが動かなかったためにこのような方法で概算しています。 ↩
-
真面目にやるならM=1についてもモデルを過程して、尤度の高いほうを選ぶとかすればよさそう。その場合は1モデルあたりのギブスサンプリングの反復回数が減るので、どっちがいいか悩みどころ。eivourさんはMCMCを使わないモデルをいくつか持ち、M=2でDが小さい時の尤度が高い場合のみ今回説明したモデルを使っていました。 ↩
-
観測データを知った時の確率分布 ↩
-
パラメータが与えられたときに観測データが得られる確率(密度)を表す関数 ↩
-
$x \sim \mathcal{N}(\mu, \sigma^2)$ は、$x$が平均$\mu$、分散$\sigma^2$の正規分布に従うことを意味します。 ↩
-
条件付き期待値の期待値は元の期待値に等しい ↩
-
全体の分散は条件付き分散の期待値と条件付き期待値の分散の和に分解できる ↩
-
$a \propto b$: $a$が$b$に比例することを意味する ↩
-
$\prod_{t=1}^n x_t$は$x_1 \times x_2 \times \dots x_n$ ↩