はじめに
本記事では、AHCの過去問のネタバレを多く含みます。自力で一から試す腕試しをしたい場合は注意してください。
本記事における「典型手法」は著者の見解であり、人によって考えは異なります。
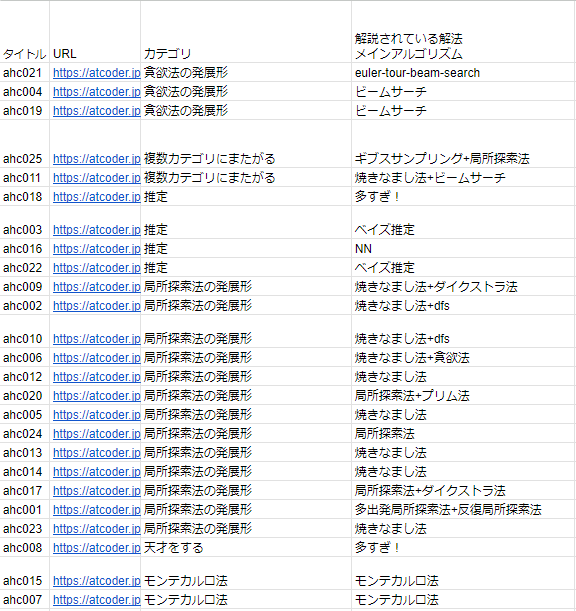
先日、今までのAHCの上位解法まとめスプレッドシートを公開しました。
AHCの解法を分類することで、AHCで使える典型手法を抽出しようと考えたためです。
このまとめの結果として、「貪欲法の発展形、局所探索法の発展形、モンテカルロ法、推定、いずれかの組み合わせ、その他」に分けられそうでした。
一方で、ヒューリスティックコンテスト初心者の方にとっては、いきなりAHCの問題にこれらのアルゴリズムを適用するのは難しいとも考えています。
そこで、典型手法をピックアップして各コンテストの問題で適用する過程を解説することで、初心者でも気軽に典型手法を使えるようになることを目指します。
これまでのシリーズ記事
今のところ執筆済みの記事を紹介します。
| 大カテゴリ | 小カテゴリ | 記事名(URL) |
|---|---|---|
| 典型手法 | モンテカルロ法 | AHC典型解法シリーズ第1弾「モンテカルロ法」 |
| 典型手法 | 焼きなまし法(山登り法含む) | AHC典型解法シリーズ第2弾「焼きなまし法」 |
| 典型手法 | ベイズ推定 | AHC典型解法シリーズ第3弾「ベイズ推定」 |
| 典型手法 | ビームサーチ (焼きなましとの合わせ技含む) | AHC典型解法シリーズ第4弾「ビームサーチ」 |
| 典型手法 | MCMC | AHC典型解法シリーズ第5弾「MCMC」 |
| 集計 | 解法まとめ | ahcまとめ(thunder) |
| 全般の進め方 | 基本的なローカルテスト | AHC初心者向け、ローカルテスタの使い方 |
AHCにおける典型手法の重要性
さて、前節では各コンテストを典型手法に分類したと説明しましたが、「AHCを始めるにあたって、典型手法を覚えないと全く話にならない」という主張をするつもりはありません。
というのも、AHCよりも過去のAtCoderのヒューリスティックコンテストの中には典型手法の効率を極めるだけで上位を狙える例もありますが、近年は典型手法をただ適用するだけでは上位を狙えないものがほとんどです。
単純なルールベース手法が、典型手法のシンプルな適用に勝ることすらよくあります。
一方で、一桁順位をとるような最上位勢は多くの場合、典型手法のいずれかを利用しています。彼らは、問題特性に応じた工夫を典型手法に加えることで、ルールベース手法やシンプルな典型手法の適用を超えるスコアを達成しているのです。
まとめると、以下のような傾向がありそうです。
典型手法に問題特性に応じた工夫を加える
>> 問題特性に応じたルールベース手法
≧ シンプルな典型手法
最初のうちは典型手法を覚えなくてもAHCを楽しむことはできますが、より高みを目指したいという上昇志向のある方は典型手法を覚えるとよいでしょう。
典型手法「モンテカルロ法」とAHC015
焼きなまし法、ビームサーチ等がヒューリスティックコンテストで有効であることは広く知られつつあり、文献も豊富である観点から、今回はあえてモンテカルロ法を紹介します。
本記事では、モンテカルロ法が有効な問題としてAHC015を紹介します。
前節で紹介した傾向「典型手法に問題特性に応じた工夫を加える >> 問題特性に応じたルールベース手法 ≧ シンプルな典型手法」がAHC015にも見られるので、まず著者の実験結果を示します。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 問題特性に応じた工夫を加えたモンテカルロ法 | 1 | 161276478 | 3506 |
| 問題特性に応じたルールベース手法 | 95 | 134104748 | 1977 |
| 問題特性を利用しない、探索部分のみに工夫を加えたモンテカルロ法 | 105 | 133207822 | 1934 |
| 問題特性を利用しない、シンプルなモンテカルロ法 | 175 | 123178860 | 1697 |
1位相当の解と95位相当の解が利用している問題特性はほぼ同じで、モンテカルロ法の適用部分だけでこれほどのスコア差がついています。
これで、モンテカルロ法を学ぶモチベーションを持っていただければ幸いです。
AHC015の問題設定
10個×10個でのキャンディーが入る正方形の空の箱があります。
この箱に100個のキャンディーを1つずつ順に追加します。
キャンディーの種類はイチゴ、スイカ、パンプキンの3種類で、t番目に受け取るキャンティーの種類は事前にわかっています。
一方、どの位置にキャンディーが追加されるかは事前にはわからず、空いてるマスから一様ランダムに選ばれます。
キャンディーを1つ追加するごとに、箱を前後左右(FBLR)のいずれか1方向に1回傾けます。
この操作を100回行った時のスコアをなるべく高くすることが目的です。
スコアの詳細は省きますが、各キャンディーの連結成分の大きさの二乗に応じてスコアが大きくなります。
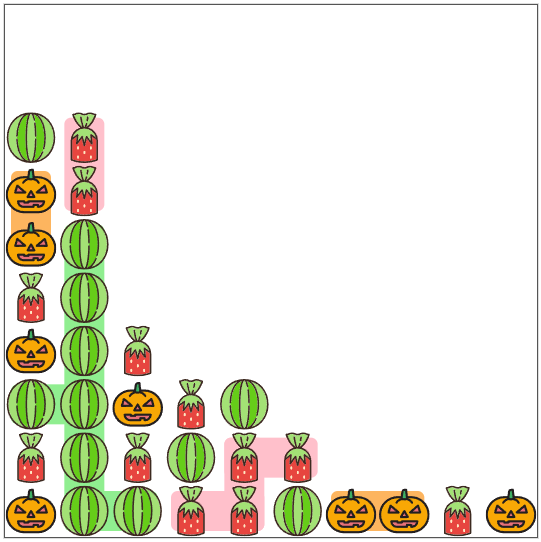
例えば、以下のように32個のキャンディーが追加済みの箱を考えます。
ここで、空いている場所からランダムな位置にキャンディーが配置されます。この位置は自分では決められません。
ここでは、パンプキンが以下の図の位置に配置されました。
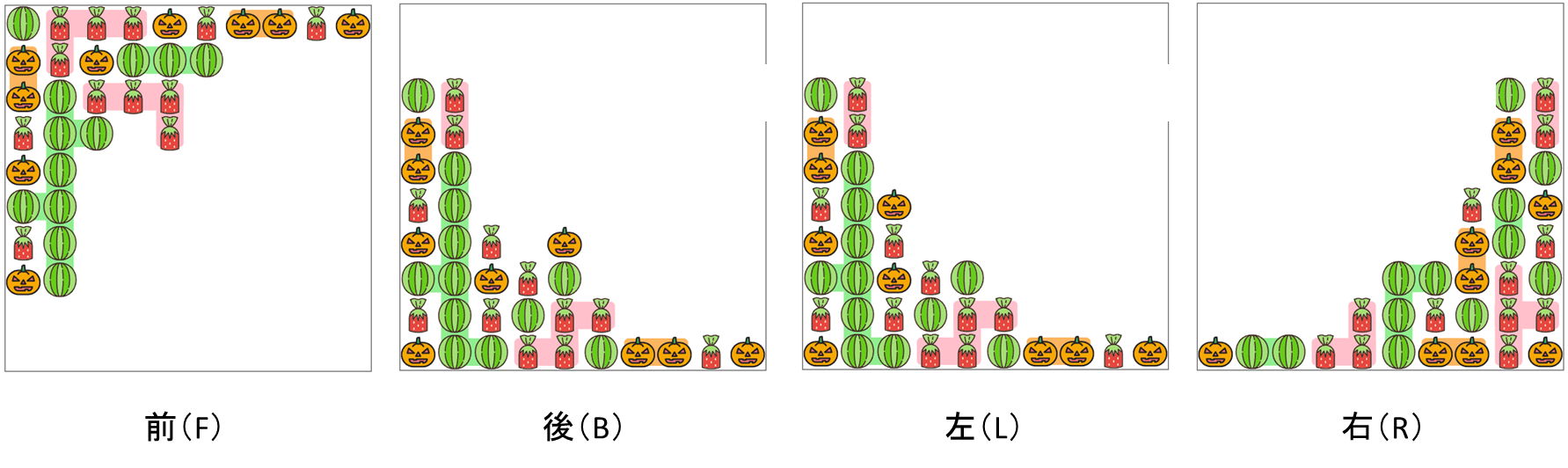
ここで、前後左右(FBLR)の4方向のいずれかに傾けます。
4方向それぞれの傾けた結果は以下の図のようになります。
この操作を100回繰り返し、以下のように100個のキャンディーが埋め尽くされたとします。
この場合、それぞれのキャンディーの連結成分(同じキャンディー同士で隣り合っているもの同士をつなぎ合わせたまとまり)とその大きさは以下のように表せます。
これらの連結成分をなるべく大きなひとまとりにすることが目的です。
そのため、理想的には以下のようにイチゴ、スイカ、パンプキンが1つずつの大きな3つのまとまりになるような状態が望ましいです。キャンディーが追加される位置がわからないので、現実的にはこの形にすることは極めて難しいですが、この形になるべく近づけることを目指します。(bowwoforeachさんのポストを参考)
問題特性を利用しない、シンプルなモンテカルロ法
手法説明
お待たせしました。ようやく本記事の主題、モンテカルロ法についてお話します。
Wikipediaの言葉を借りると、モンテカルロ法「シミュレーションや数値計算を乱数を用いて行う手法の総称」のことです。
AHC015の場合、「追加されるキャンディの位置は事前にわからない」という点が肝になります。
事前にわからない情報がある場合、乱数を用いて何度もシミュレーションすることで、わからない情報を補うことができます。
たとえば以下のようにスイカが1つ置かれた状態で、その後[スイカ、イチゴ]の順でキャンディが追加されることがわかっているとします。

ここで、2ターン分の「傾ける方向」、「追加されるキャンディの位置」を全て一様ランダムに選択してシミュレーションすることを考えます。
たとえば、乱数により「右(R)に傾ける」「スイカが15番目の空きマスに追加される」「前(F)に傾ける」「イチゴが53番目の空きマスに追加される」という候補を選択した場合、以下のように進行します。

これを100ターン分行えば、1回分のランダムなシミュレーションが完了します。この、最後までシミュレーションを行う1回の単位をプレイアウト、特に乱数によるプレイアウトをランダムプレイアウトと呼びます。プレイアウトを1回行うことで、最終的なスコアの可能性の1つを計算することができます。
ここで、ある箱の状態から、前(F)、後(B)、左(L)、右(R)に傾けた4つの状態それぞれから、1回ずつランダムプレイアウトをします。前(F)に1回傾けた状態からの1回プレイアウトしたらスコア125951になった場合、図中のように125951/1と印をつけます。
同様に4つの状態からそれぞれ100回ずつランダムプレイアウトし、それぞれのスコア合計とプレイアウト回数を記録します。この場合、各状態の将来の平均スコアが前(F): 12501438/100 = 125014.38、後(B): 12501879/100 = 125018.79、左(L): 12501311/100 = 125013.11、右(R): 12500243/100 = 125002.43だとわかります。
このことから、平均スコアの高い後(B)に傾けるのがよさそうということがわかります。
※今回のように、全ての状態から行うプレイアウト回数が完全一致している場合は、合計値だけで比較してもよいです。
実装説明
まず、これはAHC015に限った話ではないですが、制限時間ギリギリまで計算してより良い解を探したいということが多いです。
なので、まずは時間管理を行えるクラスを自作します。
// 時間を管理するクラス(ゲームで学ぶ探索アルゴリズム実践入門のサンプルとは管理方法が異なる)
class TimeKeeper {
private:
std::chrono::high_resolution_clock::time_point start_time_;
std::chrono::high_resolution_clock::time_point before_time_;
int64_t time_threshold_;
int64_t end_turn_;
int64_t turn_;
public:
// ターン制の問題で全ターン含めての制限時間(ミリ秒)と最大ターン数を指定し、
// インスタンスをつくる。
TimeKeeper(const int64_t &time_threshold, const int64_t end_turn)
: start_time_(std::chrono::high_resolution_clock::now()),
time_threshold_(time_threshold),
end_turn_(end_turn),
turn_(0) {
// メンバイニシャライザで初期化されたstart_time_の値を使うため、before_time_はメンバイニシャライザではなくコピーをする
before_time_ = start_time_;
}
// ターンとターン開始時間を更新する
void setTurn(const int t) {
turn_ = t;
this->before_time_ = std::chrono::high_resolution_clock::now();
}
// 各ターンに割り振られた制限時間を超過したか判定する。
bool isTimeOver() {
auto now = std::chrono::high_resolution_clock::now();
auto whole_diff = this->before_time_ - this->start_time_;
auto whole_count =
std::chrono::duration_cast<std::chrono::milliseconds>(whole_diff)
.count();
auto last_diff = now - this->before_time_;
auto last_count =
std::chrono::duration_cast<std::chrono::milliseconds>(last_diff)
.count();
auto remaining_time = time_threshold_ - whole_count;
auto now_threshold = remaining_time / (end_turn_ - this->turn_);
return last_count >= now_threshold;
}
};
class State {
private:
public:
// 現在のターン
int t_ = 0;
State() {}
// ゲームが終了したか判定する
bool isDone() const {
// ターン以外に判定する処理があればここに書く
return this->t_ >= END_TURN;
}
// 指定したactionで1ターン進める
void advance(const int action) {
// 問題に合わせた処理
++this->t_; // ターンを進めるのを忘れずに(実装方針次第ではここで管理しなくてもよい)
}
// ランダムに盤面を更新する
void randomUpdate() {
// parameter をなんらかの方法で乱数生成する処理をここに書く
update(parameter);
}
// 指定したパラメータで盤面を更新する
void update(int parameter) {
// 問題に合わせた処理。引数の数は1個とは限らない
}
// スコアを取得する
double getScore() const {
double score = 0;
// 問題に合わせた処理
return score;
}
};
次に、問題設定の盤面をシミュレートするためのクラスを用意します。
class State {
private:
public:
// 現在のターン
int t_ = 0;
State() {}
// ゲームが終了したか判定する
bool isDone() const {
// ターン以外に判定する処理があればここに書く
return this->t_ >= END_TURN;
}
// 指定したactionで1ターン進める
void advance(const int action) {
// 問題に合わせた処理
++this->t_; // ターンを進めるのを忘れずに(実装方針次第ではここで管理しなくてもよい)
}
// ランダムに盤面を更新する
void randomUpdate() {
// parameter をなんらかの方法で乱数生成する処理をここに書く
update(parameter);
}
// 指定したパラメータで盤面を更新する
void update(int parameter) {
// 問題に合わせた処理。引数の数は1個とは限らない
}
// スコアを取得する
double getScore() const {
double score = 0;
// 問題に合わせた処理
return score;
}
};
上記で用意した時間管理クラスと盤面管理クラスを用いて、モンテカルロ法を実装します。
// モンテカルロ法に関連する名前空間
namespace montecarlo {
// ランダムに行動を決定する
int play1turn(const State &state) {
return legal_actions[mt() % (legal_actions.size())];
}
// ランダムプレイアウトをして勝敗スコアを計算する
double playout(State state) {
state.advance(play1turn(state));
int before_turn = state.t_;
while (!state.isDone()) {
state.randomUpdate();
state.advance(play1turn(state));
}
return state.getScore();
}
// 制限時間(ms)を指定して行動を決定する
int primitiveMontecalro(TimeKeeper &time_keeper, const State base_state) {
std::vector<double> w(legal_actions.size());
for (int simulate_cnt = 0;; simulate_cnt++) {
if (time_keeper.isTimeOver()) {
break;
}
for (int d = 0; d < legal_actions.size(); d++) {
auto state =
base_state; // 現在の状況に戻す。参照ではなくコピーである点に注意
state.advance(d);
state.randomUpdate();
if (state.isDone()) {
w[d] += state.getScore();
} else {
w[d] += playout(state);
}
}
}
int ret = -1;
double best = -1;
for (int d = 0; d < legal_actions.size(); d++) {
if (w[d] > best) {
ret = d;
best = w[d];
}
}
return ret;
}
} // namespace montecarlo
この実装方針をベースにAHC015に適用した提出では、スコア123178860を達成しました。これはコンテスト時換算で175位 perf1697相当です。
サンプルコードのつもりでコメントマシマシで提出しているので、細かい実装が気になる方はこちらの提出コードも参考にしてください。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 問題特性を利用しない、シンプルなモンテカルロ法 | 175 | 123178860 | 1697 |
おまけ
上記で紹介したモンテカルロ法は原始モンテカルロ法と呼ばれる手法で、将来の操作を全てランダムに行う前提なので、あまり現実的な動きをシミュレーションできません。
そこで、将来的な動きも含めて探索を行うMCTSという手法があります。
この考え方を応用した実験も行ったので、その結果も載せておきます。原始モンテカルロ法よりは良い結果になりました。
こちらの提出コードはきれいに清書していないため、見づらい点もあるかと思いますがご容赦ください。
MCTSについて詳しく知りたい方は、ゲームで学ぶ探索アルゴリズム実践入門~木探索とメタヒューリスティクスをご参照ください。
わかる人向けの説明:AHC015に適用する場合、展開済みのノードも毎回乱数を用いて再計算する必要がある点に注意してください。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 問題特性を利用しない、探索部分のみに工夫を加えたモンテカルロ法 | 105 | 133207822 | 1934 |
問題特性に応じたルールベース手法
手法説明
本題のモンテカルロ法だけで175位相当、工夫次第で105位相当のスコアを達成できました。
さて、ここでモンテカルロ法から離れてルールベース解法について説明します。
これは問題特性に応じて自分で一から考える必要があるため、他のコンテストで再現性がある方針ではない点に注意してください。
AHC015では、イチゴ、スイカ、パンプキンのキャンディの3種類のキャンディについて、なるべく同種同士をひとまとめの場所に配置することが目的です。
これは、例えば、「イチゴは後ろの方にまとめる」、「スイカは右前にまとめる」、「パンプキンは左前にまとめる」と決めてしまえば目的を達成しやすそうです。

これを実現する方法を考えましょう。
まず最初に思い浮かぶのは、「入力から位置を受け取った、今追加されたばかりのキャンディがイチゴなら後ろ(B)、スイカなら右(R)、パンプキンなら左(L)に傾ける」という方針です。
| 今のキャンディ | 今傾ける方向 |
|---|---|
| イチゴ | 後ろ(B) |
| スイカ | 右(R) |
| パンプキン | 左(L) |
例えば、以下のようにパンプキンが追加されたばかりの盤面を考えます。

先ほど考えたルールに従い、左(L)に傾けてみましょう。
確かにパンプキンを左に寄せる目的は果たしましたが、イチゴがパンプキンよりも前側に追加されてしまいました。
イチゴは後ろの方にまとめるつもりだったので、これはうれしくないですね。

そこで、次に追加される予定のキャンディがイチゴだということは事前に知っているので、それを利用できないか考えます。
例えば、先ほどのパンプキンが追加された盤面に戻り、前(F)に傾けてみましょう。
お、今度はイチゴが元のイチゴのまとまりの後ろ側に出現していい感じですね。
そう、キャンディが出現する位置は「空きマスのどこか」なので、前(F)に傾けると、今存在するどのキャンディよりも後ろ側に次のキャンディが追加されるように強制することができます。

そのため、次のキャンディを基準にルールを考えます。
| 次のキャンディ | 今傾ける方向 |
|---|---|
| イチゴ | 後ろ(B) |
| スイカ | 右(R) |
| パンプキン | 左(L) |
実は、これでもまだ不十分です。
例えば、以下のようにイチゴが追加され、次にスイカが追加される予定の盤面を考えます。
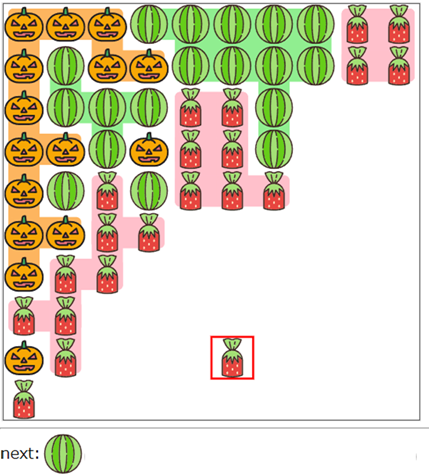
先ほど考えたルールに従い、左(L)に傾けてみましょう。
なんと、イチゴのまとまりの下にスイカがまぎれてしまいました。

この場合、今追加されたイチゴを考慮して後ろ側に傾けるのがよさそうです。
無事、イチゴのまとまりに紛れるのを回避してスイカが追加されました。

以上を踏まえると、今のキャンディと次のキャンディを両方考慮したルールが必要です。
例えば、横方向を考慮する必要ないイチゴを起点に考えると、スイカとパンプキンの区別を気にしなくてよいので以下のようなルールを考えます。
| 今のキャンディ\次のキャンディ | イチゴ | スイカ | パンプキン |
|---|---|---|---|
| イチゴ | 前(F) | 後ろ(B) | 後ろ(B) |
| スイカ | 前(F) | - | - |
| パンプキン | 前(F) | - | - |
後はイチゴの絡みを気にしなくてよい、言い換えれば縦方向の動きを気にしなくてよいので、次のキャンディの都合がいい向きに傾けるルールにすればよいです。
| 今のキャンディ\次のキャンディ | イチゴ | スイカ | パンプキン |
|---|---|---|---|
| イチゴ | 前(F) | 後ろ(B) | 後ろ(B) |
| スイカ | 前(F) | 左(L) | 右(R) |
| パンプキン | 前(F) | 左(L) | 右(R) |
実装説明
これはモンテカルロ法の実装と比べると非常に簡単に実装できます。
以下のように、上で説明した表の通りの二次元配列を用意し、現在のキャンディと次のキャンディに従って操作列を埋めていくだけでよいです。
なお、イチゴは1、スイカは2、パンプキンは3で、1-indexedである点は注意して実装してください。
下記の例では、表を0-indexedで持った上で取り出しの際にキャンディを0-indexedに変換しています。
// ルールベースに従う操作列を記録する配列
vector<int> rule_actions(END_TURN, -1);
// イチゴは後ろに、スイカは右前に、パンプキンは左前に集める
vector<vector<int>> rule_action_samples = {
{F, B, B},
{F, L, R},
{F, L, R},
};
for (int t = 0; t < END_TURN - 1; t++)
{
int now = nexts[t];
int next = nexts[t + 1];
// キャンディを0-indexedに変換してルールを取得
rule_actions[t] = rule_action_samples[now - 1][next - 1];
}
この実装方針をベースにAHC015に適用した提出では、スコア134104748を達成しました。これはコンテスト時換算で95位 perf1977相当です。
問題特性を利用しないモンテカルロ法では、スコア123178860、探索部を工夫しても133207822だったので、それより良い結果と言えます。
こんなにも簡単な実装でモンテカルロ法に勝ててしまいました。
問題特性をうまく利用することがとても重要だということがわかります。
「ヒューリスティックコンテスト?なんか典型手法をただ適用するだけの覚えゲーなんでしょ?つまんなそう」そんな外部の声が聞こえてきたらこのルールベース解法の強さをつきつけてやりましょう。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 問題特性に応じたルールベース手法 | 95 | 134104748 | 1977 |
問題特性に応じた工夫を加えたモンテカルロ法
手法説明
ここまで、モンテカルロ法の適用方法と、それすら上回るルールベース解法の説明をしました。
ここまでの説明を見て、間違っても「ルールベースが強いので、モンテカルロ法などのアルゴリズムを覚える必要はない」なんて思わないでくださいね。
ここからが本当の闘いです。
ルールベース解法は非常に高速に処理できるため、2秒という制限時間を大量に余らせてしまいます。
そこで、ルールベース解法を用いて探索して、よりよい解を見つけることを目指します。
モンテカルロ法におけるプレイアウトは、必ずしも完全なランダムプレイアウトする必要はありません。
先ほど適用したプレイアウトは、大きく分けて二つの要素をランダムにシミュレーションしています。
- 自分のプログラムでは制御できない情報(今回の場合、将来のキャンディの位置)
- 自分のプログラムで制御できる情報(今回の場合、傾ける操作)
将来のキャンディの位置は制御不能なのでランダムにシミュレーションする意味がありますが、傾ける操作は制御可能なので、わざわざランダムにシミュレーションする必要がありません。
そこで、現在注目しているターン以外の将来の操作は、先ほど考えたルールベース解法で置き換えることができます。
実装説明
実は実装自体は非常に簡単です。
先ほどのモンテカルロ法のコードとルールベース解法のコードを両方コピーした後、
play1turn部分をルールベース解法に置き換えるだけでよいです。
// モンテカルロ法に関連する名前空間
namespace montecarlo {
// 1ターン分の行動を決定する
int play1turn(const State &state) {
- return legal_actions[mt() % (legal_actions.size())];
+ return rule_actions[state.t_];
}
} // namespace montecarlo
また、上で説明した以外に、追加されるキャンディ位置の乱数を各傾き方向の探索時に同じもので使いまわすことで、より平等な評価にすることも有効です。
これは、以下のようにrandomUpdateで利用した乱数を外だしして前計算すれば実現できます。
+ // 1ターン1方向あたりの最大シミュレーション回数
+ constexpr int SIMULATION_MAX = 14000;
+ // 探索で利用するキャンディの位置候補
+ // p_it[何回目の探索か][ターン] = キャンディの位置
+ array<array<int, END_TURN>, SIMULATION_MAX> p_it{};
class State {
// ランダムに盤面を更新する
void randomUpdate() {
+ update(p_it[simulate_cnt][this->t_]);
- int reverse_t = END_TURN - this->t_;
- int p = 1;
- if (reverse_t != 0) {
- p = mt() % reverse_t + 1;
- }
- update(p);
}
};
namespace montecarlo {
int primitiveMontecalro(TimeKeeper &time_keeper, const State base_state) {
+ // シミュレーション回数を制限する
+ for (int simulate_cnt = 0; simulate_cnt < SIMULATION_MAX; simulate_cnt++) {
- for (int simulate_cnt = 0; ; simulate_cnt++) {
// 処理内容
}
}
} // namespace montecarlo
int main() {
+ // キャンディの位置の乱数 p_itを前計算する。
+ for (int i = 0; i < SIMULATION_MAX; i++)
+ for (int t = 0; t < END_TURN; t++) {
+ int reverse_t = END_TURN - t;
+ int p = 1;
+ if (reverse_t != 0) {
+ p = mt() % reverse_t + 1;
+ }
+ p_it[i][t] = p;
+ }
}
これらの実装をAHC015に適用した提出では、スコア161276478を達成しました。これはコンテスト時換算で1位 perf3506相当です。
なお、実際のコンテストで1位だったeijirouさんの記事には、モンテカルロ法で探索する傾きの方向を4方向全てではなく期待値の低い方向を枝刈りする方針も記載されていましたが、それはしなくてもこのスコアを達成することができました。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 問題特性に応じた工夫を加えたモンテカルロ法 | 1 | 161276478 | 3506 |
最後に
本記事では、主に以下の2つを紹介しました。
- 過去のAHCに共通して使えそうな典型解法を抽出した
- 典型解法の1つである、モンテカルロ法の具体的な使い方を示した
AHCが単純に典型解法を使うだけで勝てるほど甘くないこと、あるいは典型解法なしで勝てるほど甘くないことが伝わったかと思います。
典型解法を覚え、問題特性に応じて武器として使える程度に習熟することが大事になります。
今回の記事の評判と著者のやる気次第で、本記事をシリーズ化し、今回抽出したAHCの典型解法全てを解説するようなことができたらおもしろいなぁなんて考えています。
正直めちゃたいへんなので挫折しそう