はじめに
記事中に「ゲームで学ぶ探索アルゴリズム実践入門~木探索とメタヒューリスティクス」についての言及が何度か登場しますが、この本を呼んでいなくても本記事の説明だけで完結するようにしたつもりなのでご安心ください。
本記事では、AHCの過去問のネタバレを多く含みます。自力で一から試す腕試しをしたい場合は注意してください。
本記事はAHC典型解法をまとめたシリーズ記事の第2段です。
シリーズ全体の目的や方針は第1段を参照ください。
これまでのシリーズ記事
今のところ執筆済みの記事を紹介します。
| 大カテゴリ | 小カテゴリ | 記事名(URL) |
|---|---|---|
| 典型手法 | モンテカルロ法 | AHC典型解法シリーズ第1弾「モンテカルロ法」 |
| 典型手法 | 焼きなまし法(山登り法含む) | AHC典型解法シリーズ第2弾「焼きなまし法」 |
| 典型手法 | ベイズ推定 | AHC典型解法シリーズ第3弾「ベイズ推定」 |
| 典型手法 | ビームサーチ (焼きなましとの合わせ技含む) | AHC典型解法シリーズ第4弾「ビームサーチ」 |
| 典型手法 | MCMC | AHC典型解法シリーズ第5弾「MCMC」 |
| 集計 | 解法まとめ | ahcまとめ(thunder) |
| 全般の進め方 | 基本的なローカルテスト | AHC初心者向け、ローカルテスタの使い方 |
典型手法「焼きなまし法(山登り法含む)」とAHC002
今回は焼きなまし法の例題としてAHC002を扱います。
問題の説明は後述しますが、この問題は工夫しないと焼きなまし法が適用できず、焼きなまし法の典型問題とは言い難い問題です。
その観点ではAHC001などの方が素直かもしれません。
一方で、AHCでは素直に典型手法を適用できないことも多いです。
今後も典型手法そのまま、といった問題は減っていくことが予想されるため、あえて素直でない問題を焼きなます過程を説明することを考えました。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 近傍を工夫した焼きなまし法 | 1 | 6352173 | 3512 |
| 焼きなまし法 | 1 | 6283426 | 3512 |
| 山登り法 | 13 | 5863983 | 2680 |
| 深さ優先探索(DFS) | 355 | 2907007 | 1354 |
AHC002の問題設定
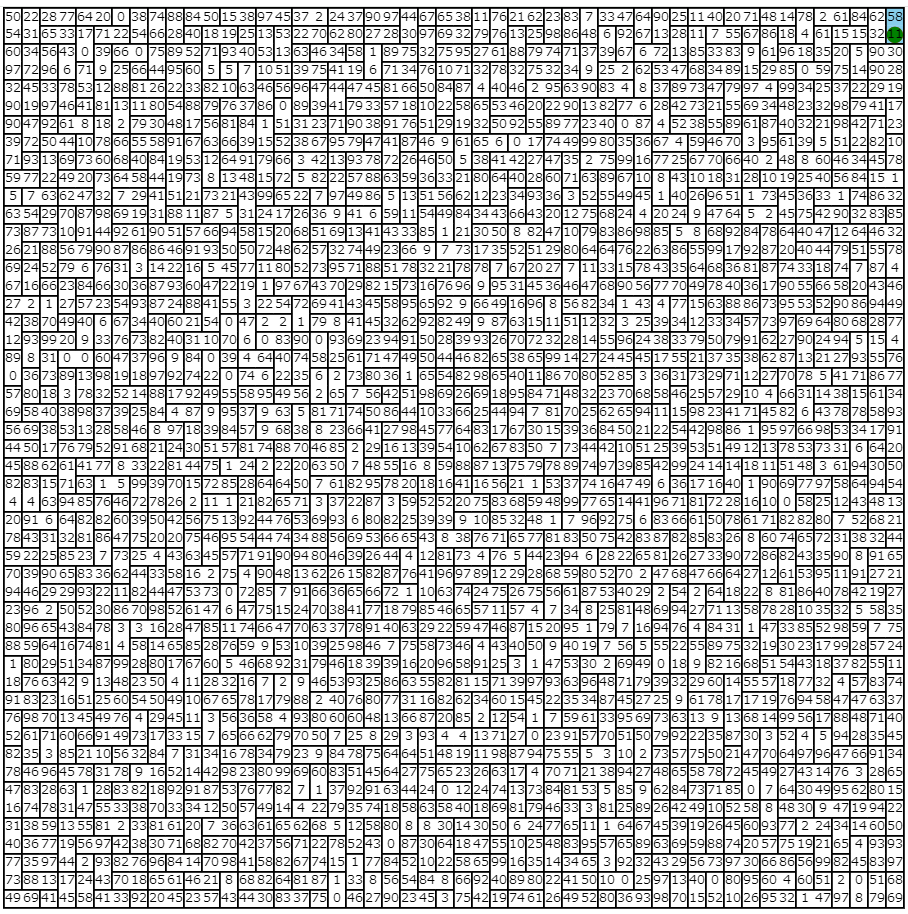
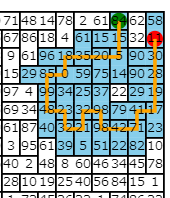
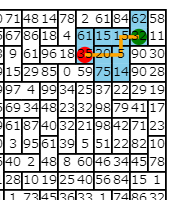
50×50マスの床に最大2マス分の大きさのタイルがランダムに敷き詰められています。
ランダムに与えられた初期位置からスタートして、縦横4方向(DRUL)に進みながら、なるべく多くのポイントを稼ぐことが目的です。
例えば、左(L)、下(D)、下(D)の経路を辿ると、経路上のポイント(11,32,90,90)の合計223がスコアとなります。
注意点として、既に踏んだタイルはもう一度踏むことができません。2マスで構成されているタイルの場合、2マスともが侵入禁止になる点に注意してください。この場合、左(L)、下(D)への移動は可能ですが、右(R)、上(U)への移動は不可能です。
目指す形
まず最初に、焼きなまし法系の手法に共通する流れを軽く説明します。
- 初期解を生成する
- 解の一部を変えながらよりよい解を探す
ゲームで学ぶ探索アルゴリズム実践入門~木探索とメタヒューリスティクスの例では初期解をランダムに生成しましたが、今回の問題では制約を守る解を生成するのが難しいです。
そのような問題では、初期解の生成方針も問題に応じて考える必要があります。
そのため、まずは初期解の生成から説明し、その後に山登り法と焼きなまし法を説明していきます。
初期解の生成
手法説明
まず最初にできることとして、とりあえず進めるだけ進んでみます。
そうすると、どこかで行き止まりになってしまい、これ以上進めなくなります。
行き止まりになる前に戻ってみましょう。
先ほどとは異なる方向に移動してみましょう。先ほどと違い、さらにもう一歩進めそうです。
このように、行き止まりになる度に前の状態に戻って異なる選択を繰り返せば、このようにかなり多くのタイルを踏める、つまり多くのポイントが獲得できるようになります。
このように、進めるだけ進めてこれ以上進めなくなったら元に戻って違う方向に進む、を繰り返す手法を深さ優先探索(DFS)と呼びます。
DFSは本記事の主題ではないですが、AHCでよく使う手法なので覚えておいてもいいです。
実装説明
DFSの用途はいろいろあるので書き方はいろいろありますが、今回の問題で書いた書き方を簡単にまとめると以下のようになります。
今回の主題はDFSではないので細かい説明は省きますが、再帰関数の引数を増やしすぎると書くのがめんどうなので、今回はクラスのメンバ変数で制御する仕組みにしました。
AHC002で具体的にどのようにスコアを更新したりパスを追加したりしているかについては、こちらの提出を参照してください。
// 始点を指定して探索するクラス
class DfsSolver {
public:
vector<int> path_; // coordのリスト。今探索中のパス
vector<int> best_path_; // coordのリスト。今のところ一番いいパス
int best_score_ = 0; // 今のところ一番いいスコア
int score_ = 0; // 今探索中のパスのスコア
int remaining_search_cnt_; // 残り探索回数
// dfsを開始する。dfsは再帰で実装するので開始する関数が必要
void start() {
// 必要なら各変数を初期化
remaining_search_cnt_ = 探索回数;
dfs(探索を開始する位置);
}
private:
// coordを始点とした探索
void dfs(const int coord) {
path_.emplace_back(coord);
score_ = なんらかの処理;
// スコアがよくなればパスを更新
if (best_score_ < score_) {
best_score_ = score_;
best_path_ = path_;
}
// 残り探索回数を減らして終了判定
remaining_search_cnt_--;
if (remaining_search_cnt_ == 0) return;
// 次の場所を探す
vector<int> legal_next_coords;
for (const auto &next_coord : next_coords[coord]) {
if (next_coordが未探索で条件を満たすなら) {
legal_next_coords.emplace_back(next_coord);
}
}
// 条件を満たす隣の場所を探索する
for (const auto &next_coord : legal_next_coords) {
// 再帰
dfs(next_coord);
// 探索済みなら終了
if (remaining_search_cnt_ == 0) return;
}
// パスを元に戻す
path_.pop_back();
score_ = なんらかの処理;
探索済みフラグを戻す;
}
};
この実装方針をベースにAHC002に適用した提出では、スコア2907007を達成しました。これはコンテスト時換算で355位, perf1354相当です。AHC002で正の得点を出した人は1018人いるので、半分以内にはなりました。これだけできればAHCに熱い気持ちで打ち込めている頃ではないでしょうか。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 深さ優先探索(DFS) | 355 | 2907007 | 1354 |
山登り法
手法説明
ある解から少し構造を変えた解の集合を近傍と呼びます。山登り法は、近傍からランダムな解を選択して評価し、今よりもスコアが改善すれば解を遷移する、スコアが改善しなければ解を選択し直す、を繰り返す手法です。
「目指す形」で先述した流れを山登り法の説明に合わせて詳細にまとめると以下のようになります
- 初期解を生成する
- 近傍解を1つ評価する
- 近傍解を評価し、今の解よりも良いなら近傍解に遷移する
- 2~3を繰り返す
これは、必ず改善する方に解が遷移するので、非常に汎用性が高く使いやすい手法です。
では、AHC002で山登り法を適用してみましょう。
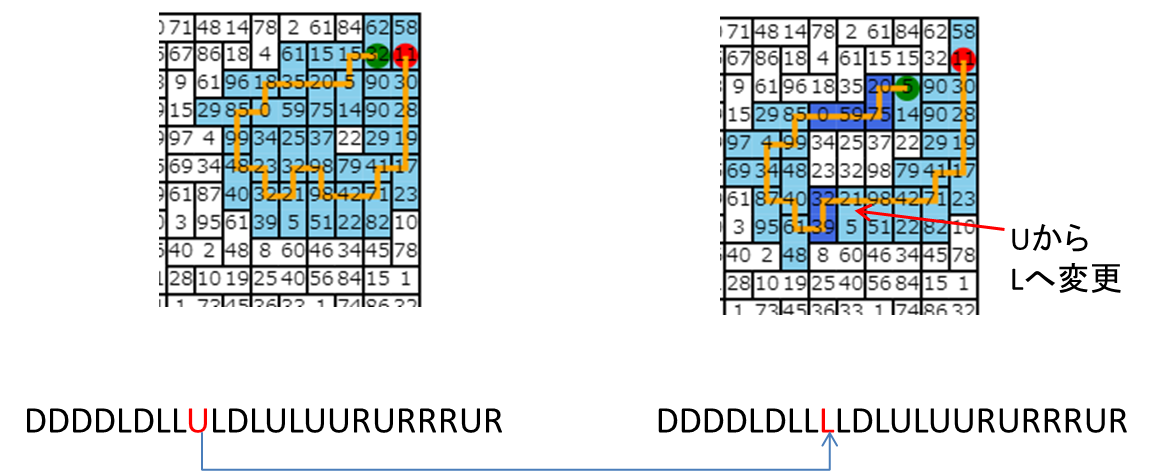
例えば、単純な近傍だと「操作列のどれか1つを異なる方向に変える」などが考えられます。
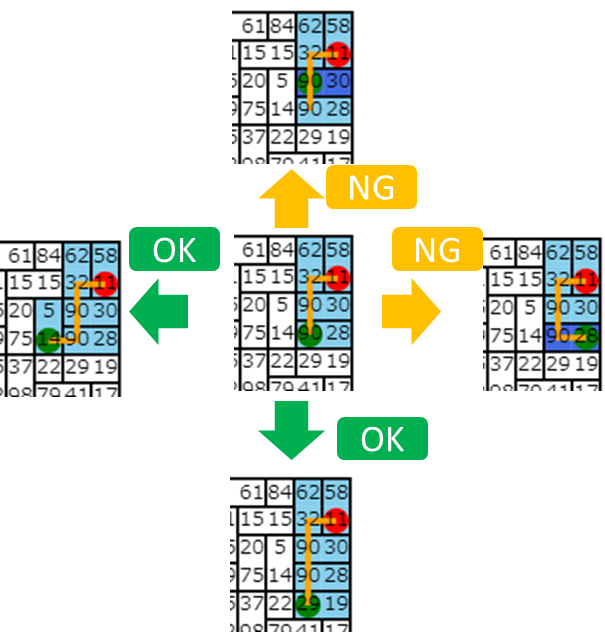
例えば、解「DDDDLDLLULDLULUURURRRUR」からランダムに選んだ位置、9回目の操作をランダムな方向Lに変更した解「DDDDLDLLLLDLULUURURRRUR」を見てみましょう。9回目の操作をした時点では問題ルールに背いていないですが、その後の操作で同じタイルを何度も踏んでいます。
というのも、10回目以降の操作は9回目の操作がUであることを前提に決定したものなので、9回目の操作が別のものになった場合に10回目移項の操作がルールに沿っていることを保証できません。このような背景から、順序性のある問題で山登り法を適用するには少し工夫が必要です。
さて、近傍を考えるとしても、解の性質を何も考えずに変えても意味がないことがわかりました。
今考えてうまくいかなかった近傍を深堀りして考えてみましょう。
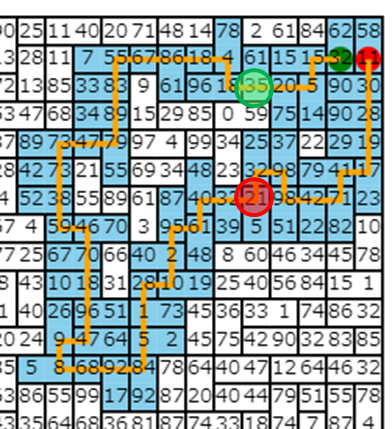
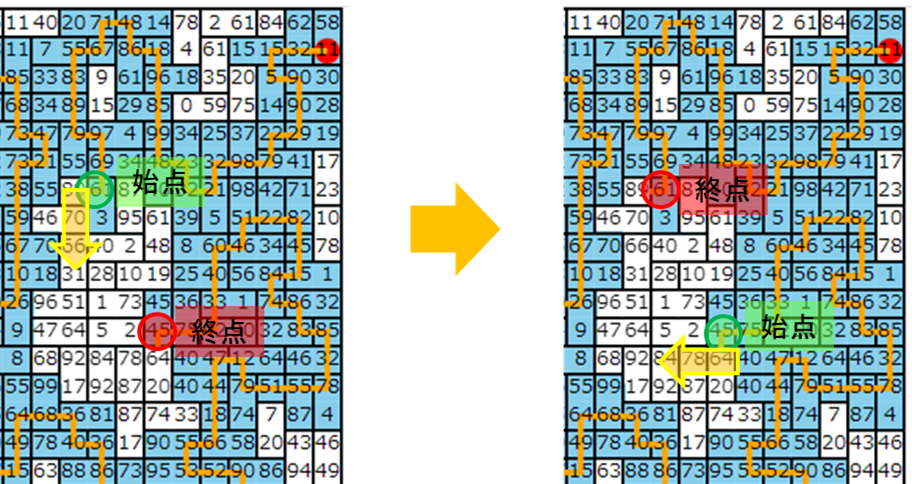
9回目の操作の変更をしましたが、8回目の操作までの「DDDDLDLL」の部分を変化させなければ、ここまではルールを守っているはずです。
視点を変えると、後半の操作も、始まる位置さえ正しければ同じルートを保ことができます。
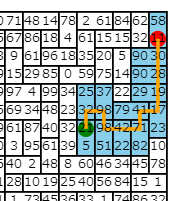
以下の図は、位置(2,45)から操作[RRUR]をする例
ここまで考えると、前半の一部のルートと後半の一部のルートをそのまま残した上で、残りの中間の操作で位置(2,45)にさえたどり着ければ、ルールを守りつつ異なるルートが辿れそうです。
残したルートで踏んだタイルの位置と、新しく考えたい中間ルートの初期位置と最終位置さえわかれば、初期解同様にDFSで新しいルートを作ることができます。
元のルートではスコア920、今回のルートではスコア2216なので、スコアが改善しました。
このようにパスを付け替えれる操作でスコアが改善したら操作後のパスを暫定解とし、また別のパスをランダムに選んでパスを付け替えるのを繰り返せば、徐々にスコアがよくなるはずです。
これが山登り法です。
なお、今回のように、解を大きく変更するが意味のある近傍操作を利用する手法を大近傍探索法、もしくは巨大近傍法などと呼びます。
実装説明
山登り法は以下のような方針で実装できます。
AHCでは制限時間があるので、先述の流れの他に時間計測も必要です。
以下のコード中のTimeKeeperDoubleが何をしているのか、AHC002で具体的にどのように近傍解の評価や遷移をしているかについては、こちらの提出を参照してください。コメントもたくさんつけてわかりやすくしたつもりなので、参考になると思います。
struct State {
vector<int> now_answer_; // 暫定解。今回の場合は今までに遷移してきた現在のパス
void hillClimbWithTimeThreshold(const int64_t time_threshold) {
/***************************************************************/
// 1. 時間計測開始
auto time_keeper = TimeKeeperDouble(time_threshold);
// end of 1
/***************************************************************/
/***************************************************************/
// 2. 初期解を生成し、ベストスコアを更新する。
// ループ前に必要な変数があれば用意する。
// 初期解生成が重すぎる場合は時間計測を分ける必要あり。
now_answer_ = なんらかの処理;
int now_score = なんらかの処理;
// end of 2
/***************************************************************/
for (;;) {
/*************************************************************/
// 3. 制限時間の確認
time_keeper.setNowTime();
if (time_keeper.isTimeOver()) {
break;
}
// end of 3
/*************************************************************/
/*************************************************************/
// 4. 近傍から1つ選んでスコアを計算
vector<int> next_answer = なんらかの処理;
// end of 4
/*************************************************************/
/*************************************************************/
// 5. 試した近傍を反映させる(遷移する)
// ※実装方針次第では4の段階で反映させ、
// 5では遷移させたくない場合に元の状態に戻す方針もできる
int diff = next_score - now_score;
if (diff > 0) {
now_answer_ = next_answer;
}
// end of 5
/*************************************************************/
}
}
};
この実装方針をベースにAHC002に適用した提出では、スコア5863983を達成しました。これはコンテスト時換算で13位, perf2680相当です。
DFSで生成した初期解から大きくスコアが伸びたことがわかりますね。橙パフォーマンスなんて出した日には界隈でちょっとした有名人になってしまうのではないでしょうか。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 山登り法 | 13 | 5863983 | 2680 |
焼きなまし法
手法説明
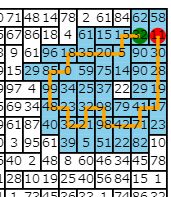
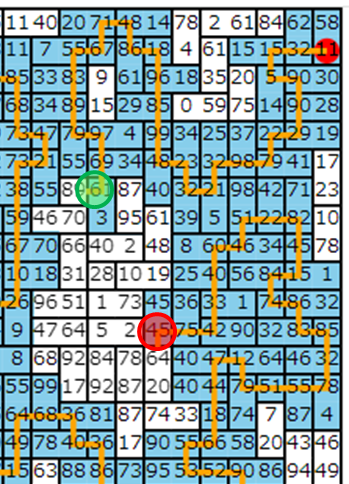
さて、先ほどの山登り法を適用した例として、以下のような経路ができます。
盤面のほとんどを埋め尽くす、かなりよさそうな経路に見えますね。
このまま山登り法を続けて見ましょう。
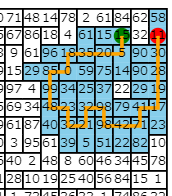
以下は先ほどと同じようにパスを切った例です。
盤面のほとんどのタイルが既に踏まれているため、先ほどの例と比べて、かなり窮屈になっていますね。この場合、パスを付け直しても前回と同じパスになってしまうか、前回よりスコアの低いパスしか見つからないです。
このように、どの近傍解も今より良くならない解のことを局所最適解と呼びます。
この問題に限らず、どの問題でもかなり多くの場合は山登り法を適用すると局所最適解から解が改善しなくなります。
そこで、局所最適解から抜け出せるようにしましょう。
山登り法ではスコアが改善する解にしか遷移しないようにしていましたが、スコアが改善しない解にも遷移するようにします。
そうすると一回分の近傍ではたどり着かない解にも到達することになるので、改善する可能性が生まれます。
しかし、スコアが改善しない解でも必ず遷移するようにすると、今度は全く解が改善する方向に進みません。そのため、解の遷移をちょうどよく制御したいです。
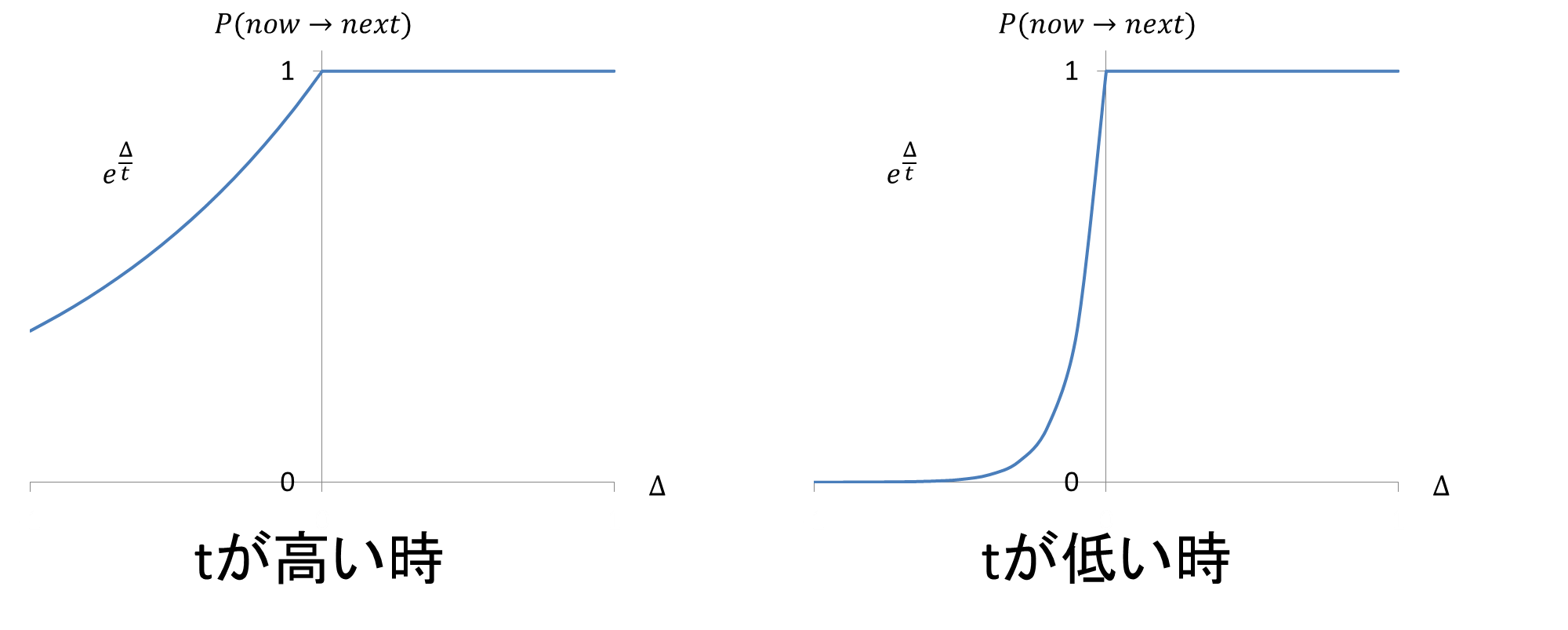
ここで、ある解$now$のスコアを$Score(now)$としたとき、ランダムに選択した解$next$に遷移するかどうかを考えます。まず、$Score(next)>=Score(now)$の時はnextに遷移します。$Score(next)<Score(now)$の時は、変化量$\Delta=Score(next)-Score(now)$に応じた確率で遷移するようにします。
遷移確率は$e^{\Delta/t}$とします。パラメータ$t$は温度と呼ばれ、$t$が高いほど遷移確率が高く、$t$が低いほど遷移確率が低くなります。探索の初期は温度を高くすることでランダムな遷移を発生しやすくします。
このように温度を徐々に冷やしながらよりよい状態を探す工程を、金属工学における焼きなましから名前をとり、焼きなまし法(Simulated Annealing)と呼びます。
なお、焼きなまし法を紹介する文献の中には遷移確率を$e^{-\Delta/t}$とすることがあります。これは、スコアを最小化することと最大化することのどちらを目的とするかによって変わります。今回はスコアを最大化することを目的として説明したため、遷移確率は$e^{\Delta/t}$としました。
実装説明
実装は山登り法からほんの少し変えるだけでいいです。
手順4の温度パラメータを計算する部分、手順6で温度とスコアの改悪量に応じて遷移する部分を加えればもう焼きなまし法!
お手軽すぎる、、!!
struct State {
vector<int> now_answer_; // 暫定解。今回の場合は今までに遷移してきた現在のパス
void simulatedAnnealingWithTimeThreshold(const int64_t time_threshold) {
/***************************************************************/
// 1. 時間計測開始
auto time_keeper = TimeKeeperDouble(time_threshold);
// end of 1
/***************************************************************/
/***************************************************************/
// 2. 初期解を生成し、ベストスコアを更新する。
// ループ前に必要な変数があれば用意する。
// 初期解生成が重すぎる場合は時間計測を分ける必要あり。
now_answer_ = なんらかの処理;
int now_score = なんらかの処理;
// end of 2
/***************************************************************/
for (;;) {
/*************************************************************/
// 3. 制限時間の確認
time_keeper.setNowTime();
if (time_keeper.isTimeOver()) {
break;
}
// end of 3
/*************************************************************/
/*************************************************************/
+ // 4. 焼きなましの温度と遷移の閾値を決定する。
+ // 以下の例ではstart_tempから経過時間に応じて線形にend_tempに冷却する。
+ // 冷却スケジュールは線形である必要はない。
+ double temp =
+ start_temp +
+ (end_temp - start_temp) * (time_keeper.getNowTime() / time_threshold);
+ // end of 4
/************************************************************/
/*************************************************************/
// 5. 近傍から1つ選んでスコアを計算
vector<int> next_answer = なんらかの処理;
// end of 5
/*************************************************************/
/*************************************************************/
// 6. 試した近傍を反映させる(遷移する)
// ※実装方針次第では5の段階で反映させ、
// 6では遷移させたくない場合に元の状態に戻す方針もできる
int diff = next_score - now_score;
+ if (exp(diff / temp) > rnd.nextDouble()) {
now_answer_ = next_answer;
}
// end of 6
/*************************************************************/
}
}
};
この実装方針をベースにAHC002に適用した提出では、スコア6283426を達成しました。これはコンテスト時換算で1位, perf3512相当です。
うんうん、1位ね、なるほど、、1位!!!??なんと、13位相当の山登り法を焼きなまし法に直しただけで1位相当のスコアになってしまいました!
AHCで1位なんてとった日には、未来永劫語り継がれる伝説と言っても過言ではありません。これはもう、焼きなまし法を覚えないなんてありえないですね!
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 焼きなまし法 | 1 | 6283426 | 3512 |
さらに工夫した焼きなまし法
手法説明
さて、もう1位相当のスコアで満足しちゃいましたか?
とはいえAHC002は4時間の短期コンテストです。もしこれが長期コンテストなら、このぐらいのスコアを超える猛者はたくさん現れることでしょう。
ここからさらに工夫を加え、よりよいスコアを目指しましょう。
ここで紹介する工夫は、以下の2つです。
- 近傍を工夫する
- 遷移条件の式を見直し、足切りに利用する
まず、近傍の工夫についてです。
先述した通り、近傍をどう設計するかで焼きなまし法の性能は大きく変わります。
正直、AHC002では焼きなまし法を適用できている時点で近傍の工夫をしているようなものではあります。が、さらに工夫を加えられるか考えてみましょう。
例えば、先ほどの説明では、一度消したパスをつなぎ直す際のdfsの探索方向については言及しませんでした。
今回考えた近傍では、2つの点をdfsで繋ぐだけなので、2つの点のどちらから始めてもやりたいことを実現できます。
dfsは深くまで探索して行き止まりになった時、違うルートに戻るとしても深いところで戻る動きになるため、浅い探索タイミングでの方向の決定による影響を強く受けます。
そのため、dfsの始点と終点を逆転させることで、生成されるパスがある程度違うものになることを期待できそうです。
近傍で得られる解のバリエーションを増やすことを多様化と呼び、焼きなまし法はうまく多様化を図ることで、より良い解が得られる場合があります。
次に、遷移条件の式を見直し、足切りに利用する方法について説明します。
先ほど、遷移確率$e^{\Delta/t}$によって遷移を決める説明をしました。
これは、0以上1未満の乱数$random$を用いて、
$$e^{\Delta/t}>random$$
を評価するということです。
これは、logをとって式を移項すれば、以下のように変形できます。(eとlogの関係は高校数学の範囲なので教科書等を見ていただけると助かります、、)
$$\Delta>t \log(random)$$
これはやってること自体は同じですが、注目ポイントは右辺はスコアに関係なく計算可能という点です。
これは、近傍解についての計算をする前に遷移の閾値を決められるということです。
今回は近傍解を計算するのにもdfsのように重い計算を強いられています。
そこで、近傍解を計算している最中に、遷移するための閾値を超えた時点ですぐにその解を近傍解とみなして近傍の計算を終える、という処理を加えます。
これにより、近傍解の計算を高速化し、より多くの探索ができるようになります。
実装説明
2つ紹介した工夫のうち、近傍の工夫については実装部分は問題固有なのでここでは説明しません。どちらかといえば近傍の工夫は実装よりも考え方が重要です。
ここでは2つ目の工夫、遷移条件の式を見直し、足切りに利用する実装の説明をします。
まず、4の温度計算の時点で、乱数を生成して遷移の閾値を計算します。
次に、5の近傍解のスコアを計算する時に途中で閾値を超えたらそこで暫定解を決定します。
あとは6の条件式を先ほど変形した式に直して完成です。
struct State {
vector<int> now_answer_; // 暫定解。今回の場合は今までに遷移してきた現在のパス
void simulatedAnnealingWithTimeThreshold(const int64_t time_threshold) {
/***************************************************************/
// 1. 時間計測開始
auto time_keeper = TimeKeeperDouble(time_threshold);
// end of 1
/***************************************************************/
/***************************************************************/
// 2. 初期解を生成し、ベストスコアを更新する。
// ループ前に必要な変数があれば用意する。
// 初期解生成が重すぎる場合は時間計測を分ける必要あり。
now_answer_ = なんらかの処理;
int now_score = なんらかの処理;
// end of 2
/***************************************************************/
for (;;) {
/*************************************************************/
// 3. 制限時間の確認
time_keeper.setNowTime();
if (time_keeper.isTimeOver()) {
break;
}
// end of 3
/*************************************************************/
/*************************************************************/
// 4. 焼きなましの温度と遷移の閾値を決定する。
// 以下の例ではstart_tempから経過時間に応じて線形にend_tempに冷却する。
// 冷却スケジュールは線形である必要はない。
double temp =
start_temp +
(end_temp - start_temp) * (time_keeper.getNowTime() / time_threshold);
+ // 計算した温度から、遷移の閾値を計算する
+ double diff_threshold = temp * rnd.nextLog();
// end of 4
/************************************************************/
/*************************************************************/
// 5. 近傍から1つ選んでスコアを計算
+ // この計算の途中でdiff_thresholdを超えたらすぐに暫定解を決定して6に進む
+ vector<int> next_answer = なんらかの処理;
// end of 5
/*************************************************************/
/*************************************************************/
// 6. 試した近傍を反映させる(遷移する)
// ※実装方針次第では5の段階で反映させ、
// 6では遷移させたくない場合に元の状態に戻す方針もできる
int diff = next_score - now_score;
// 遷移の判定に、前計算した閾値を用いる
+ if (diff > diff_threshold) {
now_answer_ = next_answer;
}
// end of 6
/*************************************************************/
}
}
};
この実装方針をベースにAHC002に適用した提出では、スコア6352173を達成しました。これはコンテスト時換算で1位, perf3512相当です。
工夫前の6283426よりもさらによい結果となったのが確認できましたね!
コンテスト当時1位のats5515さんのスコアが6,255,977、
コンテスト当時2位のtouristさんのスコアが6,187,116
なので、当時の1位と2位の差よりも大きい幅でのスコア改善で、大成功と言えるでしょう。
実は、ats5515さんも今回紹介した、パスを逆順にする近傍は利用していたのですが、他に複数の工夫をされており、今回はその中でも不要な工夫を消したことでスコアが改善できたようです。
本記事の執筆において、ats5515さんのツイートや提出コードを大きく参考にしたので、先人の知恵には頭が上がらないです。
| 手法(提出URL) | 順位(当日相当) | スコア | perf |
|---|---|---|---|
| 近傍を工夫した焼きなまし法 | 1 | 6352173 | 3512 |
ビームサーチはどうか?(わかる人向け)
AHC002は、ゲームで学ぶ探索アルゴリズム実践入門~木探索とメタヒューリスティクスで「文脈のある1人ゲーム」と表現しているものです。
本記事の山登り法の節でも触れた通り、時系列に沿って操作を行うような問題では、山登り法、焼きなまし法を適用するのは難しいです。
そのため、そのような問題では時系列操作に強いビームサーチを適用するのが一般的です。
AHC002でもビームサーチを適用することはもちろんできますが、今回の問題では1位を狙えるほどよい方針ではないだろうと思われます。
今回の問題では、各マスにポイントが用意されているため、各操作をするたびに問題設定そのままのスコアを計算することができます。このスコアをそのまま評価値としてビームサーチをすればよいでしょうか?ここまで読み進めていただいているのでわかる方も多いと思いますが、この問題では行き止まりになって身動きがとれなくなることが多いです。
そのため、暫定スコアが高いかどうかより、どれだけたくさんのタイルを踏むことができたか、言い換えればどれだけの歩数を進むことができたかの方が大事です。
「暫定スコアよりも歩数の方が大事なら、歩数を評価値としてビームサーチを適用すればよいのでは?」
このような疑問が湧くかもしれませんね。しかし、シンプルな操作でビームサーチの探索木を構築した場合、比較対象となるノード同士は全て歩数が同じです。そのため、歩数を評価とすることは難しいです。
浅い探索の高評価の操作が深い探索にとっても良い結果になりやすいという性質でビームサーチは本領を発揮するため、問題特性に合った評価値でノードを比較できない今回の問題では、いい結果を得られないでしょう。
ゲームで学ぶ探索アルゴリズム実践入門~木探索とメタヒューリスティクスで示した手法選択のフローチャートは、あくまでも参考程度の大まかなものです。
実際には問題一つ一つの特性によって選択すべき手法は異なります。典型手法だからといってやり方を覚えるのではなく、各手法がどういった特性を持つのか理解した上で問題特性にあった手法を選択しましょう。
最後に
本記事では、AHCの典型解法の1つである、焼きなまし法の具体的な使い方を示しました。
焼きなまし法は、おそらく数あるAHCの典型解法の中でも最も重要性の高い手法なので、どの手法も知らない人にとっては実は第1段の記事よりも本記事の方が実用性があると言えます。
また、本記事中のいたるところに僕の提出コードへのリンクを貼っていますが、サンプルコードのつもりで丁寧に書いたので、細かい実装が気になる方は提出コードも読んでいただければと思います。
今後も僕のやる気が続く限りはこのシリーズの執筆を続けようと思いますので、この記事がいいと思っていただければ、いいねやストック等で応援いただけるとうれしいです!