はじめに
本記事では、AHCの過去問のネタバレを多く含みます。自力で一から試す腕試しをしたい場合は注意してください。
本記事はAHC典型解法をまとめたシリーズ記事の第3弾です。第2弾から1年以上経過してて遅筆で申し訳ないです。
シリーズ全体の目的や方針は第1弾を参照ください。
これまでのシリーズ記事と未執筆分の代替記事
今のところ執筆済みの記事を紹介します。
| 大カテゴリ | 小カテゴリ | 記事名(URL) |
|---|---|---|
| 典型手法 | モンテカルロ法 | AHC典型解法シリーズ第1弾「モンテカルロ法」 |
| 典型手法 | 焼きなまし法(山登り法含む) | AHC典型解法シリーズ第2弾「焼きなまし法」 |
| 典型手法 | ベイズ推定 | AHC典型解法シリーズ第3弾「ベイズ推定」 |
| 典型手法 | ビームサーチ (焼きなましとの合わせ技含む) | AHC典型解法シリーズ第4弾「ビームサーチ」 |
| 典型手法 | MCMC | AHC典型解法シリーズ第5弾「MCMC」 |
| 集計 | 解法まとめ | ahcまとめ(thunder) |
| 全般の進め方 | 基本的なローカルテスト | AHC初心者向け、ローカルテスタの使い方 |
典型手法「ベイズ推定」とAHC030
今回はベイズ推定の例題としてAHC030を扱います。
この問題は複数のクエリを用いて情報を収集した後、正しい情報を推定して出力する問題です。
推定系の問題は比較的珍しいためか、writerのwataさんによる公式解説をはじめ、多くの方が解説を書いています。
wataさんの解説は概念を理解するにはわかりやすくまとまっている一方、コードとの紐づけがないため、コードレベルで理解するのが難しいです。
コンテスト1位のterry_u16さんの記事もエントロピーの図解がとてもわかりやすいですが、やはりコードレベルでの解説ではないです。
aplysiaさんの記事はコードとの紐づけもあり、wataさんの解説では理解できない層にも易しい解説ですが、計算時間が長い点と、より複雑なケースへの対応ができていないため、そのまま提出できません。
これらの過去記事は僕自身の理解にもたいへん役立ちました。先人達に大いに感謝しつつ、本記事では上位の結果を出せるレベルの解法を、コードレベルで理解いただくことを目指します。
(これらの記事と一部酷似する内容があると思いますが、1記事でまとまっていることに重要性を感じたため、リンクで投げずに記事中に記載します。)
| 手法(サンプルコードのリンク) | 順位(当日相当) |
|---|---|
| ランダムな占いを元にベイズ推定で配置を推定 | 不明 |
| 相互情報量を最大化する占い | 不明 |
| 数を絞ったランダムなプールを用いることでM=3以上に対応 | 不明だが6位よりはかなり悪い(後述) |
| 焼きなましで尤度の高いプールを生成 | おそらく6位(後述) |
| 近傍を工夫した焼きなましで尤度の高いプールを生成 | おそらく2位(後述) |
AHC030の問題設定
$N\times N$のグリッド上の島に$M$個の油田があり、$M$個の油田の形と向きが事前にわかっています。
クエリを駆使し、油が埋蔵されているマスを全て推定します。
各クエリにはコストがかかるため、正しい推定結果を出力した時点のコストを最小化することが目的です。

例えば、以下のように油田が配置されているとします。
油田が重なる場合、重なった油田の数だけそのマスには油が埋蔵されています。(例:中央マスは2つの油田が重なっているので埋蔵量2)
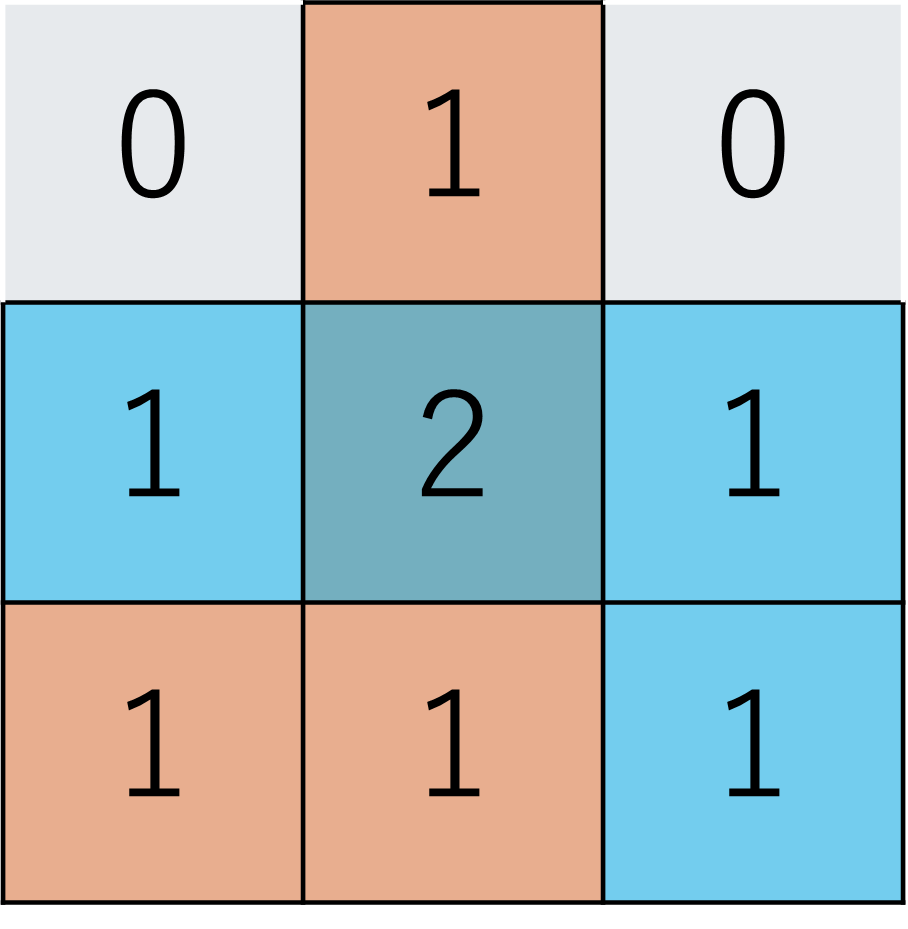
クエリは以下の3種類です。
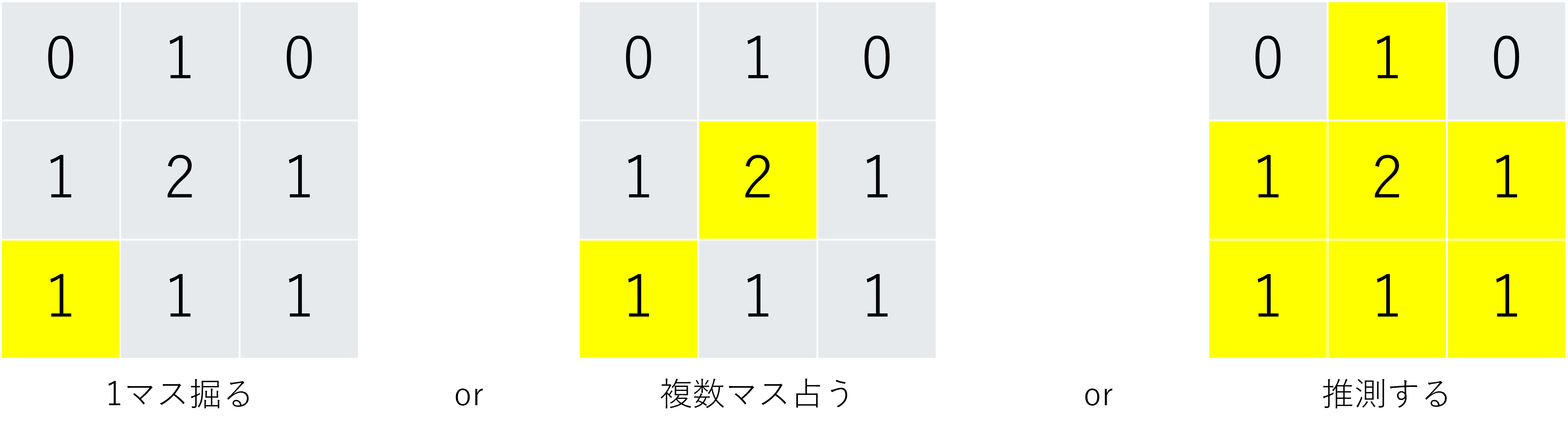
| クエリの種類 | コスト | 結果 |
|---|---|---|
| 1マス掘る | 1 | 正確な埋蔵量がわかる。 |
| kマス占う | $\frac{1}{\sqrt{k} }$ | 以下の平均$\mu$, 分散$\sigma^2$に従う正規分布からサンプルされた値を$x$として、$\max(0,\mathrm{round}(x))$が得られる。 ・$\mu=(k-埋蔵量)\epsilon + 埋蔵量(1-\epsilon)$ ・$\sigma^2=k\epsilon(1-\epsilon)$ $\epsilon$ は入力で事前に与えられる。 |
| 推測する | はずしたら1 | 正解なら終了、はずしたらコスト1を支払う。 |
占いの仕様がちょっと複雑ですね。
$\epsilon=0.1$が与えられたとき、以下の2マスを占う例を考えます。
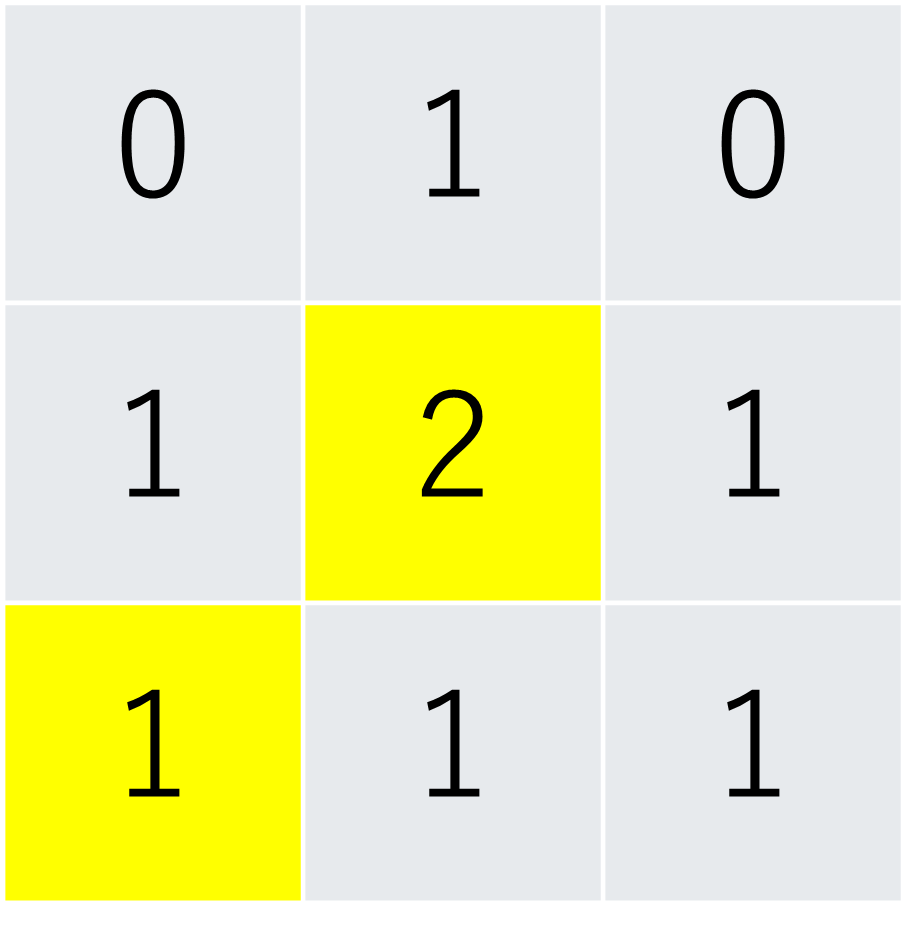
2マス占うので、$k=2$、
真の埋蔵量は$1+2=3$です。
よって、
$\mu=(2-3)0.1+3(1-0.1)=2.6$
$\sigma^2=2\times0.1\times0.9=0.18$
以下のような正規分布からサンプルされた値$x$をもとに、$\max(0,\mathrm{round}(x))$が占い結果として得られます。
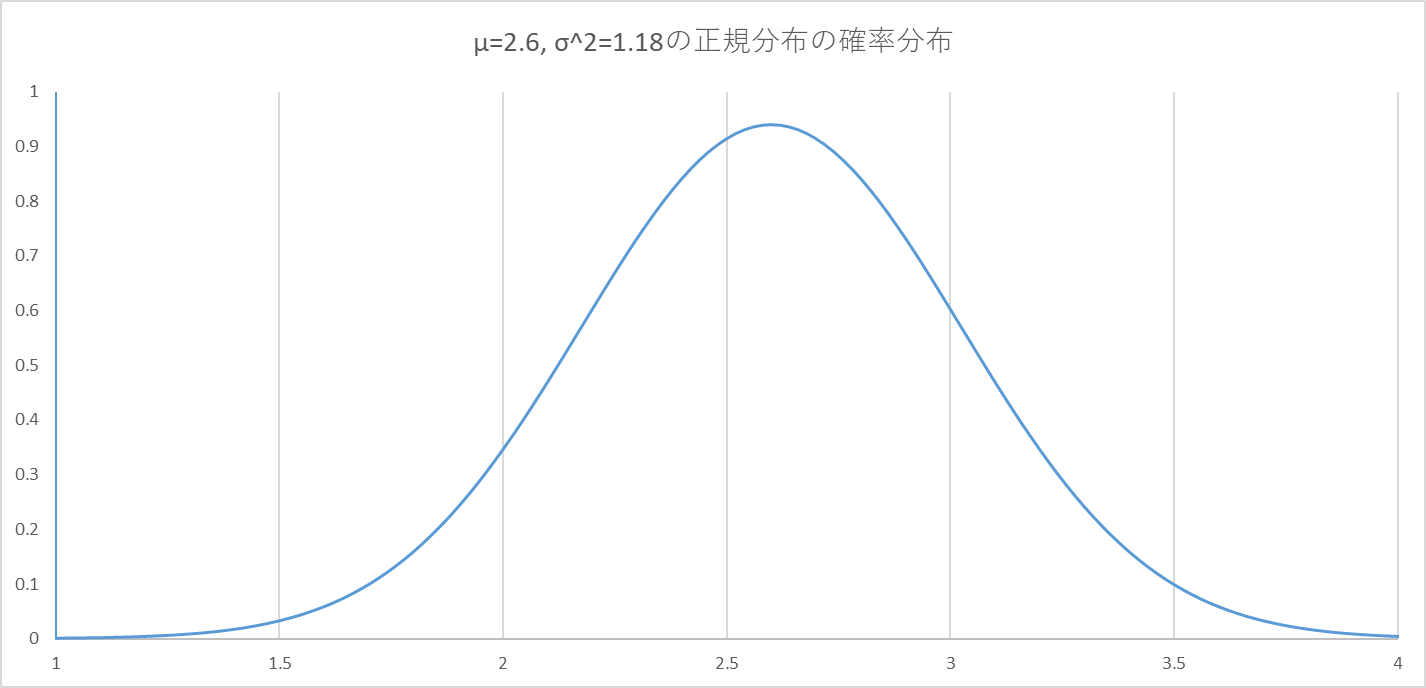
$1.5<x\leq2.5$の範囲で$\max(0,\mathrm{round}(x))=2$となるため、
以下のグラフの色をつけた面積から、約40%の確率で占い結果が2となります。
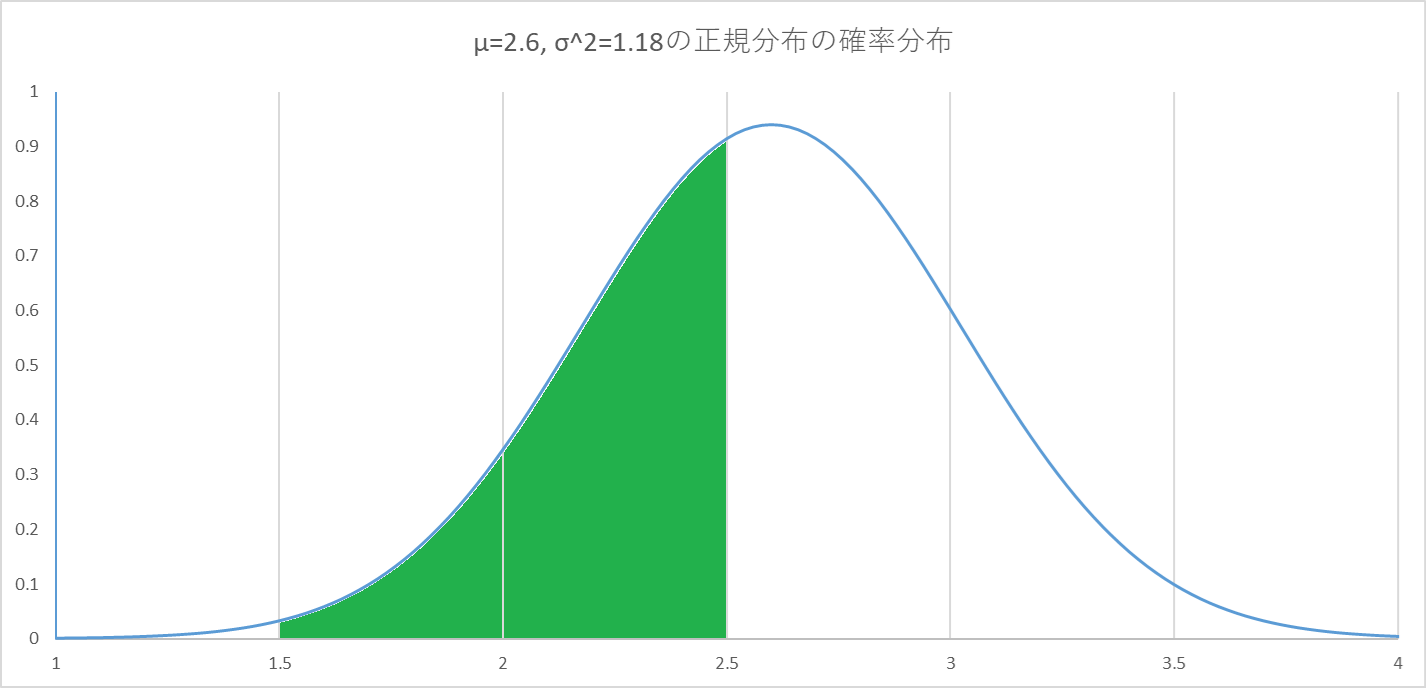
$2.5<x\leq3.5$の範囲で$\max(0,\mathrm{round}(x))=3$となるため、
以下のグラフの色をつけた面積から、約57.5%の確率で占い結果が3となります。
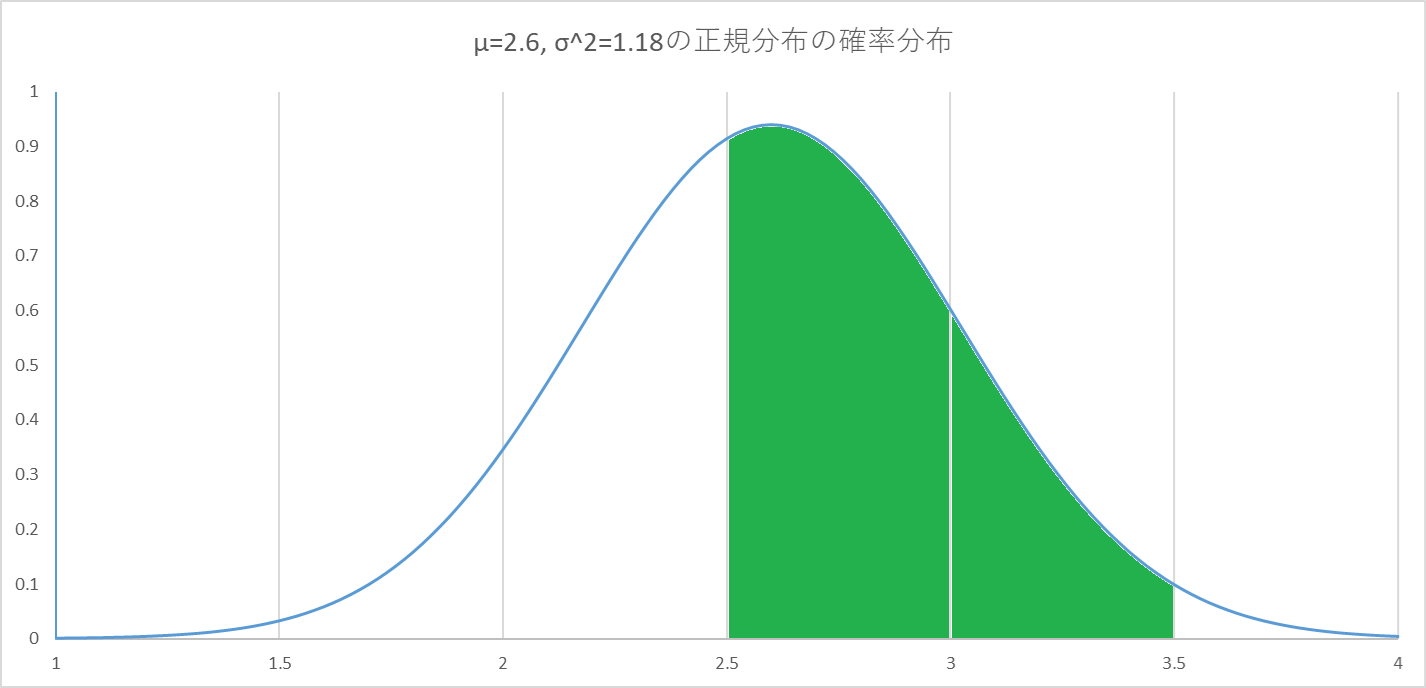
細かいことは後述しますが、今説明したように、問題文に仕様が記載されているため、「得られた占い結果がどの程度の確率で得られるものなのかは計算できる」という点を覚えておいてください。
ランダムな占いを元にベイズ推定で配置を推定
手法説明
情報を得るクエリは、1マス掘るとコスト1、kマス占うとコスト$\frac{1}{\sqrt{k}}$がかかります。
1マス掘ると埋蔵量が正確にわかりますが、kマス占うほうがコスト面でお得な気がしますね。
まずは簡単に、ランダムな占いを利用することを考えます。
この問題の目的は真の油田配置を推定することです。
占いを利用するのであれば、
「今までの占い結果が$R={r_1,r_2,\cdots,r_t}$だったとき、真の油田配置が$x_i$である確率」が高い$x_i$を見つけられればよさそうです。
「観測がBだった時にデータがAである確率」は、事後確率$P(A|B)$と呼ばれます。
事後確率はベイズの定理により、以下のように計算できます。

「今までの占い結果が$R$だったとき、真の油田配置が$x$である確率」は$P(x|R)$と表せるため、式に当てはめると以下のようになります。

周辺尤度は以下のように計算できます。
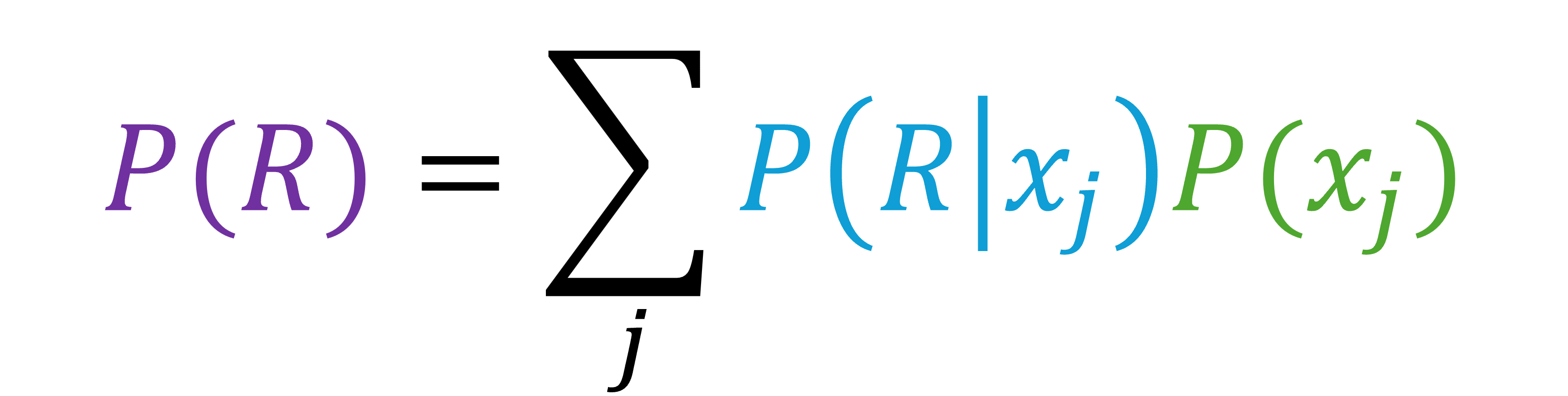
油田配置は等確率に生成されるため、事前確率$P(x)$は定数$C$として計算できます。
式を整理すると、以下のように、事後確率を求めるのに必要なのは尤度だけだとわかりました。

尤度の求め方を考えます。
占いは何度も行うので、今までの占い結果1つ1つの尤度の積を求めることで占い結果全体の尤度を求めます。
$\Pi$という記号はあまり見かけないかもしれませんが、$\Sigma (総和)$の掛け算版だと思えばいいです。

$q(k_j,s_j,r_j)$は、$k_j$マス占い、その埋蔵量が$s_j$の時、占い結果が$r_j$となる確率です。
$k_j$は$j$回目の占いで占ったマス数、$r_j$は$j$回目の占い結果なので、単に覚えておけばいいです。
$s_j$は$j$回目の占いで占ったマスの埋蔵量合計で、占いの時点ではわからない情報です。ただ、どこを占ったかを覚えていれば、配置$x$を仮定したときの埋蔵量は占いマスとの重なりから計算できます。
$q(k_j,s_j,r_j)$の計算方法については、実は先ほどの占いの仕様を説明したときに概ね説明しています。
問題文から、占い結果は
以下の平均$\mu$, 分散$\sigma^2$に従う正規分布からサンプルされた値を$x$として、$\max(0,\mathrm{round}(x))$です。
- $\mu=(k-s)\epsilon + s(1-\epsilon)$
- $\sigma^2=k\epsilon(1-\epsilon)$
$\epsilon$ は入力で事前に与えられる。
$r=\mathrm{round}(x)$とすると、$r-0.5\leq x\leq r+0.5$のどの範囲でも結果は$r$になります。
このことから、基本的には正規分布の$r-0.5\leq x\leq r+0.5$の範囲からサンプルされる確率が$q(k,s,r)$の結果となります。
正規分布で特定の範囲からサンプルされる確率は、正規分布の累積分布関数$\mathrm{CDF}$ 1を用いて計算できます。
$$
\mathrm{CDF}(x,\mu,\sigma)=\frac{1}{2}\left(1+\mathrm{erf}\left(\frac{x-\mu}{\sqrt{2}\sigma}\right)\right)
$$
$\mathrm{CDF}(x,\mu,\sigma)$は正規分布から$x$以下の値がサンプルされる確率です。
ということは、$r-0.5\leq x\leq r+0.5$の範囲からサンプルされる確率は、
$$
\mathrm{CDF}(r+0.5,\mu,\sigma)-\mathrm{CDF}(r-0.5,\mu,\sigma)
$$
となります。
なお、占い結果は$\max(0,\mathrm{round}(x))$のため、$r=0$になるのは$-∞\leq x\leq 0.5$の範囲です。
そのため、$r=0$の尤度を求めるときだけ、
$$
\mathrm{CDF}(0.5,\mu,\sigma)
$$
を計算する点に注意してください。
実装説明
$R$の尤度の計算をするにあたり、1以下の値をかけ続けると非常に小さい値になり、doubleの精度では足りなくなります。
$P(R|x)=\prod_jP(r_j|x)$
そのため、尤度の計算は対数尤度を用いることで精度を担保します。
なお、$\ln$は$\log_e$のことです。$\Pi$が$\Sigma$に置き換わっていますが、これは$\log(a\times b)=\log(a)+\log(b)$という性質を利用しています。
$\ln(P(R|x))=\sum_j\ln(P(r_j|x))$
// 油田配置がこの状態になる確率を求める
// oil_states: M個の油田に関する情報
// volumes: 各座標の埋蔵量
// top_lefts: 油田の左上座標郡
double get_ln_pR_if_x(const vector<OilState> &oil_states, const vector<uint8_t> &volumes, const vector<size_t> &top_lefts) const
{
double ln_pR_if_x = 0.0;
for (size_t q = 0; q < queries.size(); ++q)
{
// この油田配置において、q番目のクエリで占った油田の埋蔵量の合計を求める
uint8_t S = get_query_volume(oil_states, q, top_lefts);
// ln_pr_if_s_query[q][S]は、
// q番目のクエリで占った油田の埋蔵量の合計がSのときにそのクエリの占い結果になる確率の自然対数
ln_pR_if_x += ln_pr_if_s_query[q][S];
}
return ln_pR_if_x;
}
ここで、ln_pr_if_s_queryという変数を使っています。
これは、q番目のクエリで占った油田の埋蔵量の合計がSのときにそのクエリの占い結果になる確率の自然対数ですが、get_ln_pR_if_xの中で毎回計算すると無駄なので、クエリを打った時にあらかじめ計算して再利用します。
// 指定したマスの集合の埋蔵量を占う
// query_coordinates: 占うマスの座標郡
size_t query(const vector<size_t> &query_coordinates)
{
// クエリを出力して、結果を受け取る
cout << "q " << query_coordinates.size() << " ";
for (size_t ij : query_coordinates)
{
cout << ij / n << " " << ij % n << " ";
}
cout << endl;
size_t ret;
cin >> ret;
// クエリの結果を記録する
queries.emplace_back(query_coordinates, ret);
// 結果retが得られた.
// 指定したマス集合の真の埋蔵量総量がわからないため、
// あり得る埋蔵量総量全てについて、
// 埋蔵量Sのときに結果がretになる確率P(ret|S)を求める
vector<double> ln_pr_if_s(total + 1);
size_t k = query_coordinates.size();
for (size_t S = 0; S <= total; ++S)
{
double kS = (double)k - (double)S;
double kSeps = kS * eps;
double meps = 1.0 - eps;
double mu = kSeps + S * meps;
double sigma = sqrt(k * eps * meps);
ln_pr_if_s[S] = log(likelihood(mu, sigma, ret));
}
ln_pr_if_s_query.push_back(ln_pr_if_s);
return ret;
}
1回の占いごとの尤度の計算は、占い結果が0のときに$-∞\leq x\leq 0.5$の範囲で計算する点に注意して条件分岐します。
// 平均mean, 標準偏差std_devに従う正規分布において、
// resが観測される確率を求める
double likelihood(double mean, double std_dev, size_t res)
{
double b = (double)res + 0.5;
if (res == 0)
{
return normal_cdf(mean, std_dev, b);
}
else
{
double a = (double)res - 0.5;
return normal_cdf(mean, std_dev, b) - normal_cdf(mean, std_dev, a);
}
}
CDFの計算は、誤差関数erfを用いて簡単に実装できます。erfはC++の標準ライブラリにあります。
// 累積分布関数
// 平均mean, 標準偏差std_devに従う正規分布において、x以下の確率を求める
double normal_cdf(double mean, double std_dev, double x)
{
return 0.5 * (1.0 + erf((x - mean) / (std_dev * sqrt(2.0))));
}
対数尤度を使っていたので、通常の尤度に戻し、事後確率にします。
すると、各油田配置になる確率がわかるため、自信があれば推定を行います。
先述のコードでは説明しませんでしたが、推定が間違ってた場合は記録し、get_ln_pR_if_xの計算時に同じ油田配置なら非常に低い尤度を返すように利用できます。
sort_pool(pool);
auto max_prob = pool[0].ln_pR_if_x;
// 対数尤度から尤度に戻す
// p(R|x) = exp(log(p(R|x)))
for (auto &layout : pool)
{
layout.px_if_R = exp(layout.ln_pR_if_x - max_prob);
}
// 尤度から事後確率に変換する
// p(x|R) = p(R|x)/Σp(R|x)
normalize_pool(pool);
const auto &best_layout = pool[0];
auto best_bits = input.get_positives(best_layout.top_lefts);
double best_pool_prob = best_layout.px_if_R;
set_volume(pool, input);
if (best_pool_prob > 0.9)
{
// 自信があるとき、推測をう
vector<size_t> T_vec;
for (size_t ij = 0; ij < input.n2; ++ij)
{
if (best_bits[ij])
{
T_vec.push_back(ij);
}
}
if (sim.ans(T_vec))
{
break;
}
else if (sim.failed.size() == 1)
{
state.volumes = input.get_volume(state.top_lefts);
}
}
これで、ランダムな占い結果をもとに、油田配置を推定できるようになりました。
seed0の結果を見ると、なんだかよくわからない占いを何度かした後、いきなり推定が成功しているのがわかります。
サンプルコード(ランダムな占いを元にベイズ推定で配置を推定)
相互情報量を最大化する占い
手法説明
占い結果の利用方法がわかったので、次は占いを工夫していきましょう。
占いの「良さ」を評価したいのですが、「良さ」とはなんでしょうか。
一回も占ってない状況は、すべての油田配置が等確率のため、特定の配置を推定しづらく、「良くない」です。
そのため、占った後に特定の配置を推定しやすくなると、「良い」と言えそうです。
ここで、エントロピーという概念が「不確実さ、推測しにくさ」を表すため、占いの良さを評価するのにちょうどいいです。2
$$
H(X)=-\sum_{x\in \mathcal{X}}P(x)\log_2P(x)
$$
コインの裏表のように、等確率な2事象で考えると、
$$
H(X)=-\frac{1}{2}\log_2\frac{1}{2}-\frac{1}{2}\log_2\frac{1}{2}=1
$$
となります。
普通のコインだとどっちが出るかわからないですね。
全事象が等確率ならエントロピーは最大$\log_2(N)$になり、エントロピーが高い、推測が難しいことを意味します。
しかし、もしイカサマ用に細工がしてあるコインで、90%の確率で表が出るようになっていたらどうでしょう。
普通の人なら表が出ると予想しますよね。
$$
H(X)=-\frac{9}{10}\log_2\frac{9}{10}-\frac{1}{10}\log_2\frac{1}{10}=0.469
$$
となります。
このように、エントロピーが低い場合は、推測がしやすいことを意味します。
よって、今回の問題では、占いによってエントロピーが低くなることを目指せばいいです。
問題の説明をした時と同じ、$3\times3$の島の2つの油田の配置を推定することを考えます。
占い前は、4通りの配置が等確率のため、エントロピーは最大値の$\log_2(4)=2$です。
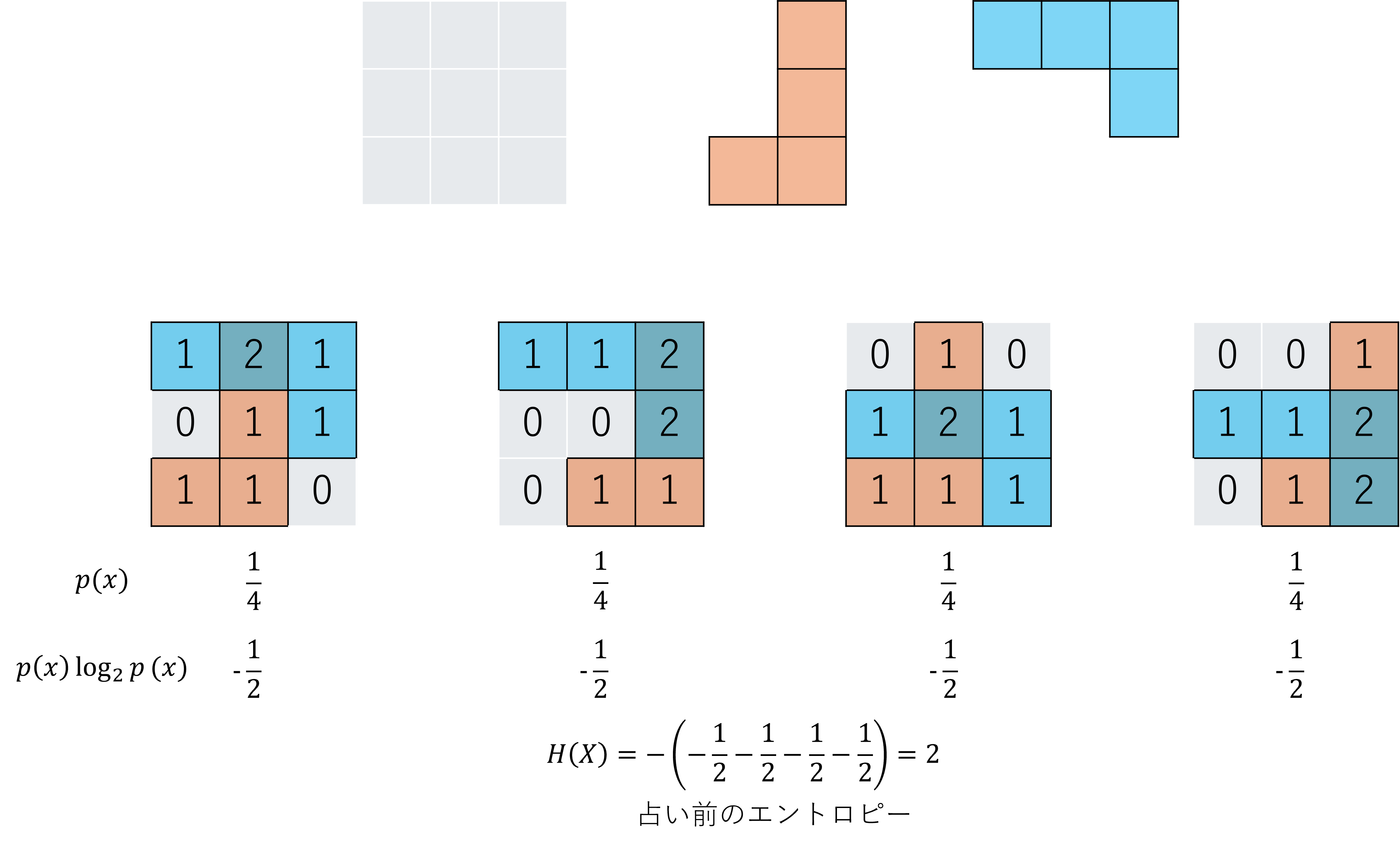
では、(0,0)のマスを占って結果が1だとわかっている場合はどうでしょう。
この場合、(0,0)のマスが1ではない2つの油田配置の可能性が消えるため、残りの2つの油田配置のみで等確率になります。
エントロピーが1になったため、占い前と比べて推測がしやすくなりました。
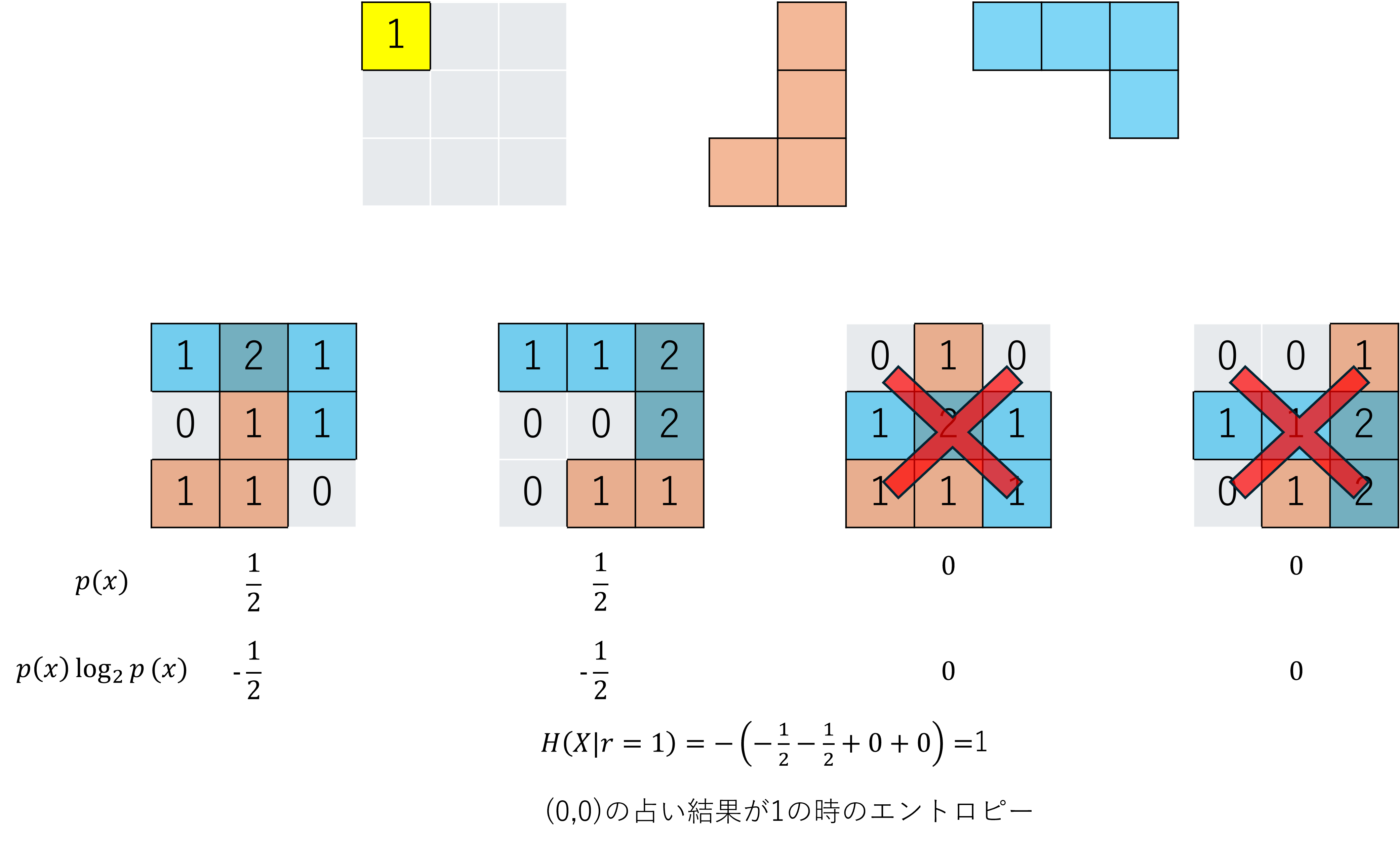
しかし、占う前に占いの結果がわからないため、考え得る占い結果すべてについて考えてみましょう。
結果が0の場合は、(0,0)のマスが0である2つの油田配置のみで等確率になり、エントロピーは1になります。
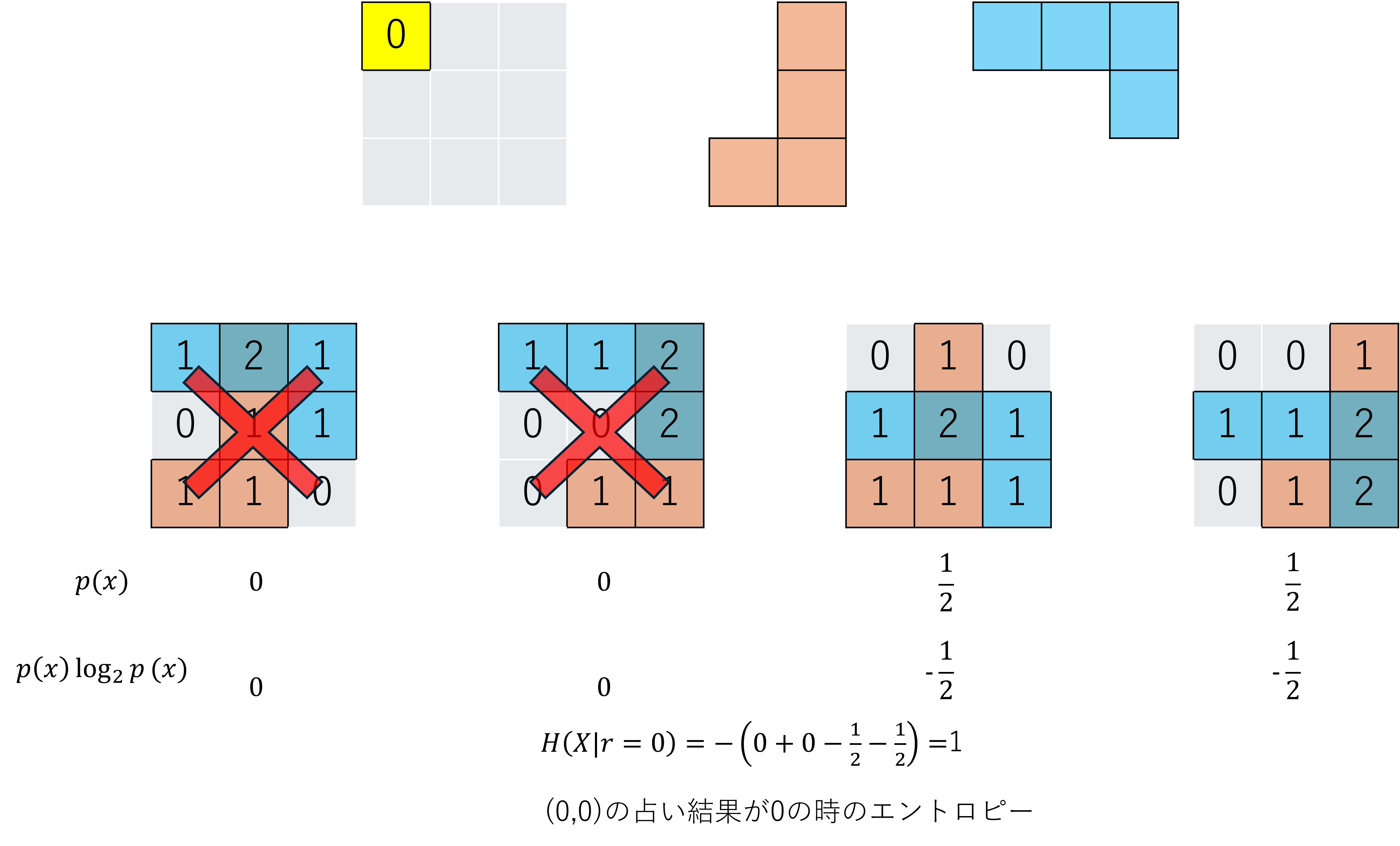
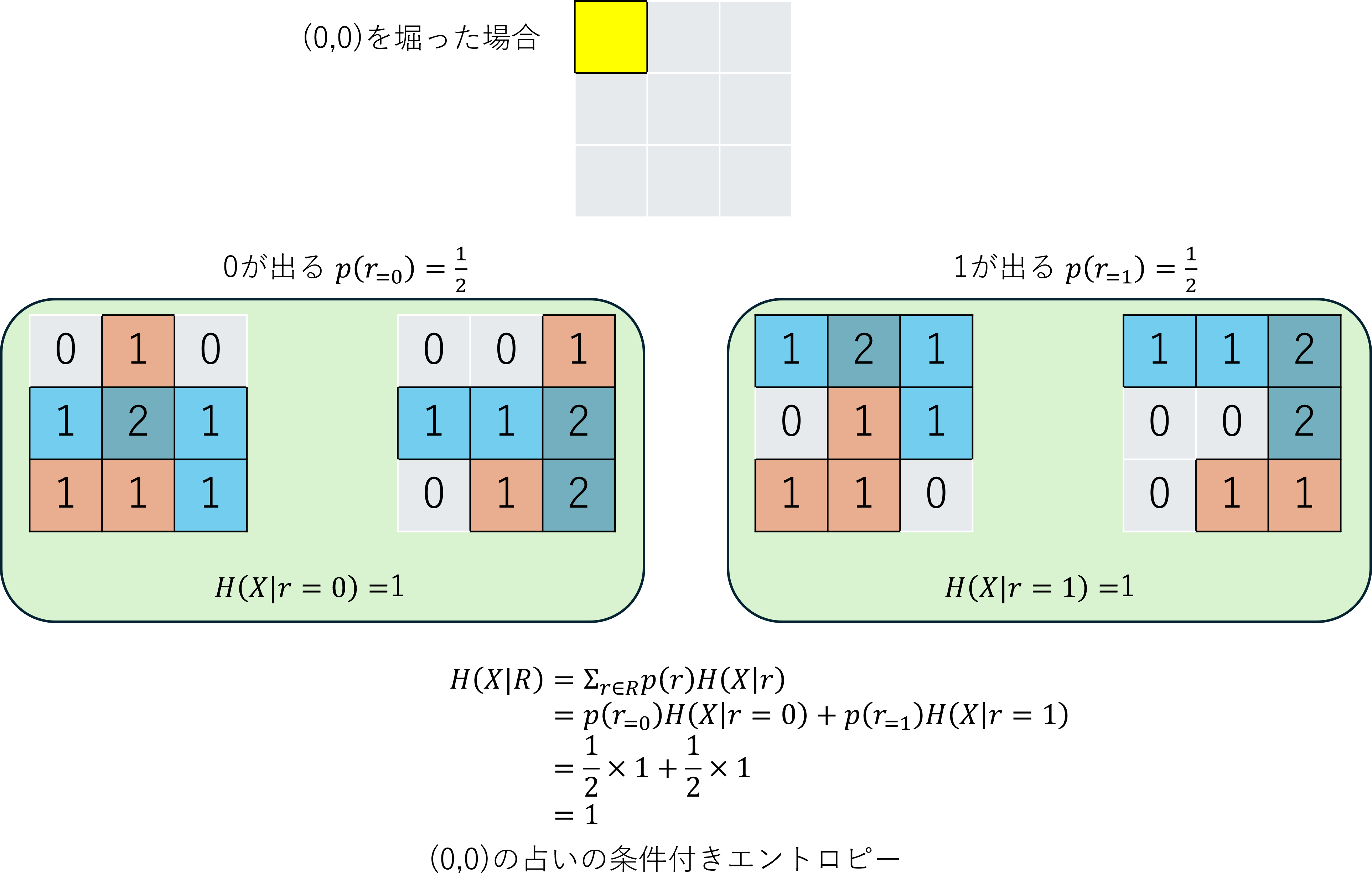
(0,0)のマスは0か1の2通りなので、これらのエントロピーの期待値を求めることで、(0,0)のマスを占った後のエントロピーが予想できます。
このように、ある事象を知ったと仮定したときのエントロピーを条件付きエントロピーと呼びます。
式で表すと、
$$
H(X|R)=-\sum_{r\in \mathcal{R}}P(r)H(X|r)
$$
となります。
同様に、(0,2)のマスを占った後の条件付きエントロピーも計算すると、$\frac{1}{2}$となります。
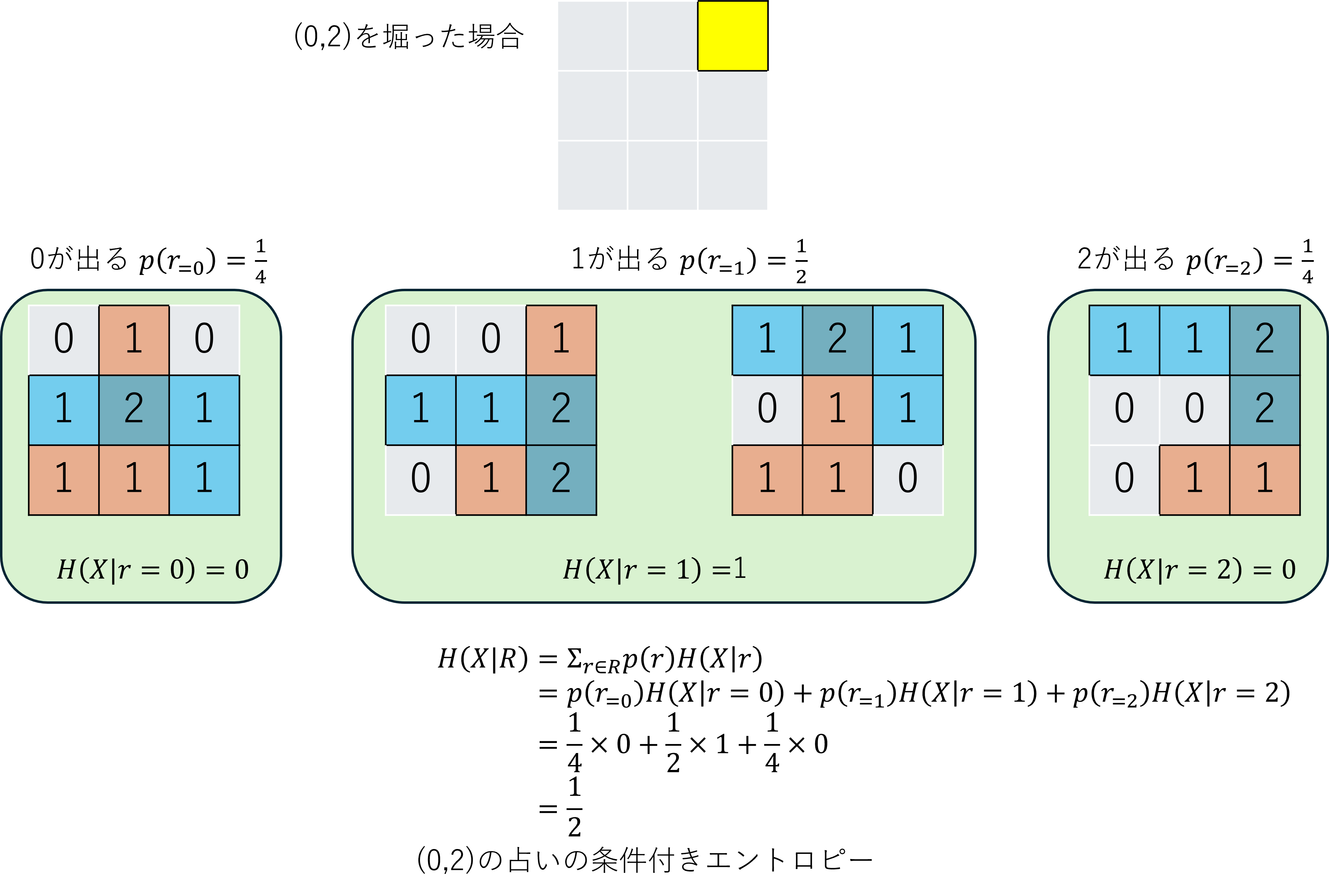
占い前のエントロピーが2だったため、
(0,0)のマスを占うことのうれしさは$2-1=1$、
(0,2)のマスを占うことのうれしさは$2-\frac{1}{2}=\frac{3}{2}$となります。
Rを観測することで減る事象Xのエントロピーの期待値を相互情報量と呼び、
$$
I(X;R)=H(X)-H(X|R)
$$
と表せます。
この問題では占いのコストをなるべくかけずに推定しやすい状態に持っていきたいため、
$$
\frac{I(X;R)}{cost}
$$
が最大の占いを行えばいいです。
相互情報量を計算しやすいように変形します。
なお、$I(X;R)=\sum_{x\in \mathcal{X}}\sum_{r\in \mathcal{R}}P(x,r)\log_2\frac{P(x,r)}{P(x)P(r)}$が一般に知られているため、wataさんの記事ではそれを紹介し、aplysiaさんの記事ではそこから式変形の過程を説明していました。
今回は$H(X)$の定義からの式変形が気になったのでがんばってみましたが、これは過剰かもしれません。
ともあれ、$P(r|x),P(x),P(r)$は計算可能なので、$\sum_{x\in \mathcal{X}}\sum_{r\in \mathcal{R}}P(r|x)p(x)\log_2\frac{P(r|x)}{P(r)}$も計算できますね。
占いの生成は、$\frac{I(X;R)}{cost}$が最大になるように山登りをすればいいです。
実装説明
評価部分をevalとして切り出せば、占いの生成はよくある山登りのコードになります。
流れとしては以下です。ループを3回で止めるのは実験的に決めた値ですが、2回だとかなり失敗しました。
- 1点だけ掘った場合の評価を計算
- 1点だけの評価の順に1点ずつクエリに加える/削除するを繰り返す山登り
- どの座標を変えても評価が変わらなくなるか、3回繰り返したら終了
// 占いクエリを取得する
vector<size_t> getDivinationQuery(
const Input &input, const vector<OilLayout> &pool,
Sim &sim)
{
// クエリを作成
Query query(input, pool);
// 全ての配置が同じ埋蔵量だと想定される座標以外で1点だけ占うクエリを評価する
vector<pair<double, size_t>> query_coordinate_evals;
for (size_t ij = 0; ij < input.n2; ++ij)
{
// 評価前後にflipを挟むことで、
// この座標1個だけでクエリを作成するときの情報量を計算する
query.flip(ij); // クエリにこの座標を含める
double ev = query.eval(sim); // クエリにこの座標を含めたときの相互情報量/コストを計算
query.flip(ij); // クエリにこの座標を含めない
query_coordinate_evals.emplace_back(ev, ij);
}
sort(query_coordinate_evals.begin(), query_coordinate_evals.end(), greater<pair<double, size_t>>());
double crt = -1e100;
for (int _ = 0; _ < 3; ++_)
{
bool change = false;
// クエリに含める座標を1つずつ増やすか減らすかして、
// 相互情報量/コストを最大化する山登り
for (const auto &[_, ij] : query_coordinate_evals)
{
query.flip(ij);
double eval = query.eval(sim);
if (crt < eval)
{
crt = eval;
change = true;
}
else
{
query.flip(ij);
}
}
if (!change)
{
// どの座標を1点変えても相互情報量/コストが変わらない場合は終了
break;
}
}
vector<size_t> query_coordinates = query.get_coordinates();
return query_coordinates;
}
占いの評価を実装します。
先ほど求めた式を使います。
$\frac{\sum_{x\in \mathcal{X}}\sum_{r\in \mathcal{R}}P(r|x)p(x)\log_2\frac{P(r|x)}{P(r)}}{cost}$
注意点として、ここで求めたいのは厳密には全く占いをしていない状態の$H(X)$と占い後の$H(X|R)$の差ではなく、今までのN回の占いをしたときの$H(X|R_N)$と今回のN+1回目の占い後の$H(X|R_{N+1})$の差です。
そのため、コード中のpxは今までのN回の占いを観測した後のpool[x].px_if_Rを使っています。
// 占いの良さを評価する
double eval(Sim &sim) const
{
size_t k = coordinate_size;
// ln_pr[r] = クエリ結果がrとなる確率の対数
// 最後にlogをとるまで、普通の確率として計算する
auto ln_pr = vector<double>();
for (size_t x = 0; x < pool.size(); ++x)
{
size_t v = volume[x];
size_t lb = sim.pr_if_x_lb[k][v];
if (ln_pr.size() < lb + sim.pr_if_x[k][v].size())
{
ln_pr.resize(lb + sim.pr_if_x[k][v].size());
}
double px = pool[x].px_if_R;
// 公式 p(r)=Σp(r|x)p(x)
// この公式を使って、p(r)を求める
for (int pi = 0; pi < sim.pr_if_x[k][v].size(); ++pi)
{
const auto &[pr_if_x, ln_pr_if_x] = sim.pr_if_x[k][v][pi];
ln_pr[lb + pi] += pr_if_x * px;
}
}
for (size_t x = 0; x < ln_pr.size(); ++x)
{
ln_pr[x] = log(ln_pr[x]);
}
// I(X;R) = ΣΣp(r|x)p(x)(log(p(r|x))-log(p(r)))
// この式を使って、相互情報量を求める
double info = 0.0;
for (size_t x = 0; x < pool.size(); ++x)
{
double px = pool[x].px_if_R;
size_t v = volume[x];
size_t lb = sim.pr_if_x_lb[k][v];
for (int pi = 0; pi < sim.pr_if_x[k][v].size(); ++pi)
{
const auto &[pr_if_x, ln_pr_if_x] = sim.pr_if_x[k][v][pi];
const auto &ln_prr = ln_pr[lb + pi];
info += pr_if_x * px * (ln_pr_if_x - ln_prr);
}
}
// コストは1/sqrt(k)なので、
// sqrt(k)倍することは、コストで割ることと同じ
// コストあたりの相互情報量を求める
return info * sqrt((double)k);
}
seed0を占うと、なんとなく真の配置の境界付近を狙って占っているようにも見えますね。

数を絞ったランダムなプールを用いることでM=3以上に対応
手法説明
さて、占いも工夫できて、占い結果を利用した推定もできたので、もうやることなさそうに見えますね。
しかし実は、ここまでの実装だけだと全てのケースに対応できません。
油田1個の配置は、$(N-油田の縦幅)\times(N-油田の横幅)$通りあります。雑に言えば約$N^2$通りです。
M個なら$|X|={(N^2)}^M=N^{2M}$通りです。($|X|$は集合$X$の要素数)
1回の占いの相互情報量を求めるのに$|X|\times|R|$回の計算が必要です。(ここで$|R|$は考えうる占い結果の数)
1マス掘りを全マス($N^2$種類)評価するだけでも、$|X|\times|R|\times N^2$回の計算が必要です。
$|X|=N^{2M}$を代入すると、
$N^{2M+2}\times|R|$回の計算が必要です。
$N$を最大値の20とした場合、
$M=2$で$6.4\times10^7\times|R|$回、$M=3$で$2.56\times10^{10}\times|R|$回の計算が必要です。
鉄則本によるとPCの処理は秒間$10^9$回程度の計算をするらしいので、$M=3$以上だと制限時間3秒に間に合いそうにないです。
そこで、あり得る油田配置を全て使って計算するのではなく、重複しないランダムな油田配置をたくさん生成し、その中で尤度が高い順にピックアップしたものを油田配置全体だと思って計算することを考えます。
実装説明
クエリを打つごとにITER個の油田配置を生成し、だいたい上位ITER*0.01個をプールに残し、このプールを全体と仮定として推定や占いを行います。
重複の判定はzobrist hashを使いますが、詳細は割愛します。
// プールに存在する配置と対数尤度を記録しておく
unordered_map<uint64_t, double> hash_ln_lilelihood;
// ~略~
// ランダムに候補を生成する
for (size_t _ = 0; _ < ITER; ++_)
{
for (size_t oil_id = 0; oil_id < input.m; ++oil_id)
{
const auto &oil = input.oils[oil_id];
size_t i = rng.randrange(input.n - oil.max_i);
size_t j = rng.randrange(input.n - oil.max_j);
state.move_to(oil_id, i * input.n + j);
}
// まだプールに追加していない配置なら追加する
if (!hash_ln_lilelihood.count(state.hash))
{
hash_ln_lilelihood[state.hash] = 0.0;
pool.emplace_back(
OilLayout{state.hash, 0.0, 0.0, state.top_lefts, state.volumes});
}
}
// ~略~
// 同じ尤度の配置を散らすためにシャッフル
shuffle(pool.begin(), pool.end(), rng);
// 対数尤度が高い順に配置候補をソート
sort_pool(pool);
// ~略~
// 閾値と時間に応じてプールを切り取る
concat_pool(pool, input, ITER);
// poolを切り取ったことで合計100%じゃなくなったので再度正規化
normalize_pool(pool);
何回占えば推定できるかわからないため、ずっと同じ個数のプールで計算すると、時間がなくなるかもしれません。
そこで、時間経過とともに残すプール数を減らします。
// プールを小さくして探索範囲を狭める
void concat_pool(vector<OilLayout> &pool, const Input &input, size_t ITER)
{
double tmp1 = ITER * 0.01;
double tmp2 = min(3.0 - get_time(), 1.0);
size_t size = min(pool.size(), max((size_t)(tmp1 * tmp2), (size_t)2));
// 尤度が低すぎる要素を削除
while (size > 2 && pool[0].px_if_R * 1e-4 > pool[size - 1].px_if_R)
{
--size;
}
if (size > 0)
{
pool.resize(size);
}
}
サンプルコード(数を絞ったランダムなプールを用いることでM=3以上に対応)
焼きなましで尤度の高いプールを生成
手法説明
さすがにランダムなプールを使うのは、真の配置を取り逃がす可能性が高そうです。
そこで、焼きなましを使って、尤度の高いプールを生成します。
焼きなましのよくある使い方は「最もよさそうな状態」を1個だけ選ぶことだと思いますが、今回は欲しい状態が1つではないため、焼きなましの途中経過もプールに残していきます。
とりあえず近傍は油田を等確率で1つ選び、その油田をランダムな位置に移動させることにします。
実装説明
焼きなましの全体像は以下の通りです。
冷却スケジュールは温度2.0から温度1.0に線形に変化させます。
void simulated_annealing(
const Input &input,
const Sim &sim,
State &state,
vector<OilLayout> &pool,
unordered_map<uint64_t, double> &hash_ln_lilelihood,
size_t ITER)
{
// 一番尤度の高い配置からスタートし、焼き鈍し法を実行することで配置候補を沢山生成する
// 途中過程で見つけた配置は、よほど小さいもの以外は全てpoolに入れる
auto bef_time = get_time();
double crt = pool[0].ln_pR_if_x;
for (size_t oil_id = 0; oil_id < input.m; ++oil_id)
{
state.move_to(oil_id, pool[0].top_lefts[oil_id]);
}
double max_crt = crt;
const double T0 = 2.0;
const double T1 = 1.0;
// TLEにならないように残り時間が少なくなったら反復回数を減らす
ITER = static_cast<size_t>(ITER * min(3.0 - get_time(), 1.0));
for (size_t t = 0; t < ITER; ++t)
{
double temp = T0 + (T1 - T0) * t / (double)ITER;
// ポリオミノをランダムに選び、ランダムな位置に移動
size_t oil_id = rng.randrange(input.m);
auto &oil = input.oils[oil_id];
size_t i2 = rng.randrange(input.n - oil.max_i);
size_t j2 = rng.randrange(input.n - oil.max_j);
size_t bk = state.top_lefts[oil_id];
state.move_to(oil_id, i2 * input.n + j2);
double next = hash_ln_lilelihood.count(state.hash) ? hash_ln_lilelihood[state.hash] : sim.ln_prob_state(state);
if (!hash_ln_lilelihood.count(state.hash))
{
hash_ln_lilelihood[state.hash] = next;
if (next - max_crt >= -10.0)
{
pool.push_back({state.hash, next, 0.0, state.top_lefts, state.volumes});
}
}
if (crt <= next || rng.gen_bool(exp((next - crt) / temp)))
{
crt = next;
}
else
{
state.move_to(oil_id, bk);
}
if (max_crt < crt)
{
max_crt = crt;
}
}
sort_pool(pool);
}
近傍の更新に使う'move_to'は指定したoil_idの油田を指定したnew_top_leftに移動させる関数です。
移動のたびにある位置の埋蔵量とvolumesと、今の配置を仮定した各クエリの占った座標集合の埋蔵量の合計を更新します。
これをメモしておくことで、対数尤度の計算時に再利用して計算量を削減できます。
class State
{
public:
vector<OilState> oil_states; // 油田の状態についてのリスト: M個
vector<size_t> top_lefts; // 油田の左上の座標. oil_satesに含めたかったが、OilLayoutにコピーして使うので別で持つ: M個
vector<uint8_t> volumes; // ある位置の油の埋蔵量: N*N個
vector<uint8_t> query_volumes; // q番目のクエリで占った座標集合の埋蔵量の合計
uint64_t hash;
const Input &input;
// 油田oil_idをnew_top_leftに移動する
// 移動自体はtop_leftsの更新だが、
// 移動に伴い、hash,query_volumes,volumesを更新する
void move_to(size_t oil_id, size_t new_top_left)
{
auto &oil_state = oil_states[oil_id];
hash ^= oil_state.hashes[top_lefts[oil_id]] ^ oil_state.hashes[new_top_left];
for (size_t q = 0; q < query_volumes.size(); ++q)
{
query_volumes[q] += oil_state.top_left_query_volumes[new_top_left][q] - oil_state.top_left_query_volumes[top_lefts[oil_id]][q];
}
if (!volumes.empty())
{
for (size_t ij : input.oils[oil_id].coordinate_ids)
{
volumes[ij + top_lefts[oil_id]] -= 1;
volumes[ij + new_top_left] += 1;
}
}
top_lefts[oil_id] = new_top_left;
}
// 今考えている配置での対数尤度を計算する
double ln_prob_state(const State &state) const
{
// ~略~
double prob = 0.0;
for (size_t q = 0; q < ln_pr_if_s_query.size(); ++q)
{
// move_toでquery_volumesを更新していたおかげで再計算しなくてよい
prob += ln_pr_if_s_query[q][state.query_volumes[q]];
}
return prob;
}
};
近傍を工夫した焼きなまし
手法説明
近傍の種類を増やしてみましょう。
以下の確率で3種類の近傍を選んで評価します。
- 30%: ランダムな油田1つを上下左右に1マス移動
- 10%: ランダムな油田1つをランダムな位置に移動
- 60%: ランダムな油田2つの位置を入れ替える
これ、確率は違うもののwataさんとeijirouさんは同じ3種類を使ってるんですよね。
まあ言われてみればそういうもんな気がしますが、上位の人達が示し合わせずに同じものにいきつくのはちょっとエモいですね。
実装説明
「ランダムな油田2つの位置を入れ替える」についてはちょっと工夫します。
オレンジの油田がある位置に緑の油田を入れ替えることを考えます。
この時、何も考えずに両者の左上座標が合うように入れ替えると、元の配置からずれないのは2マスだけです。
いろいろな解を出したいという意味ではこれでもいいですが、焼きなまし法をはじめとした局所探索法ベースのアルゴリズムでは「いい解どうしは似ている」という近接最適性を考慮します。
そのため、できれば元の配置からずれすぎないようにしたいです。
そこで、油田を入れ替える際、元の配置となるべく重複するようにずらしたいです。
この例では、右に1マスずらせば1マスぶん重複するマスが増えます。
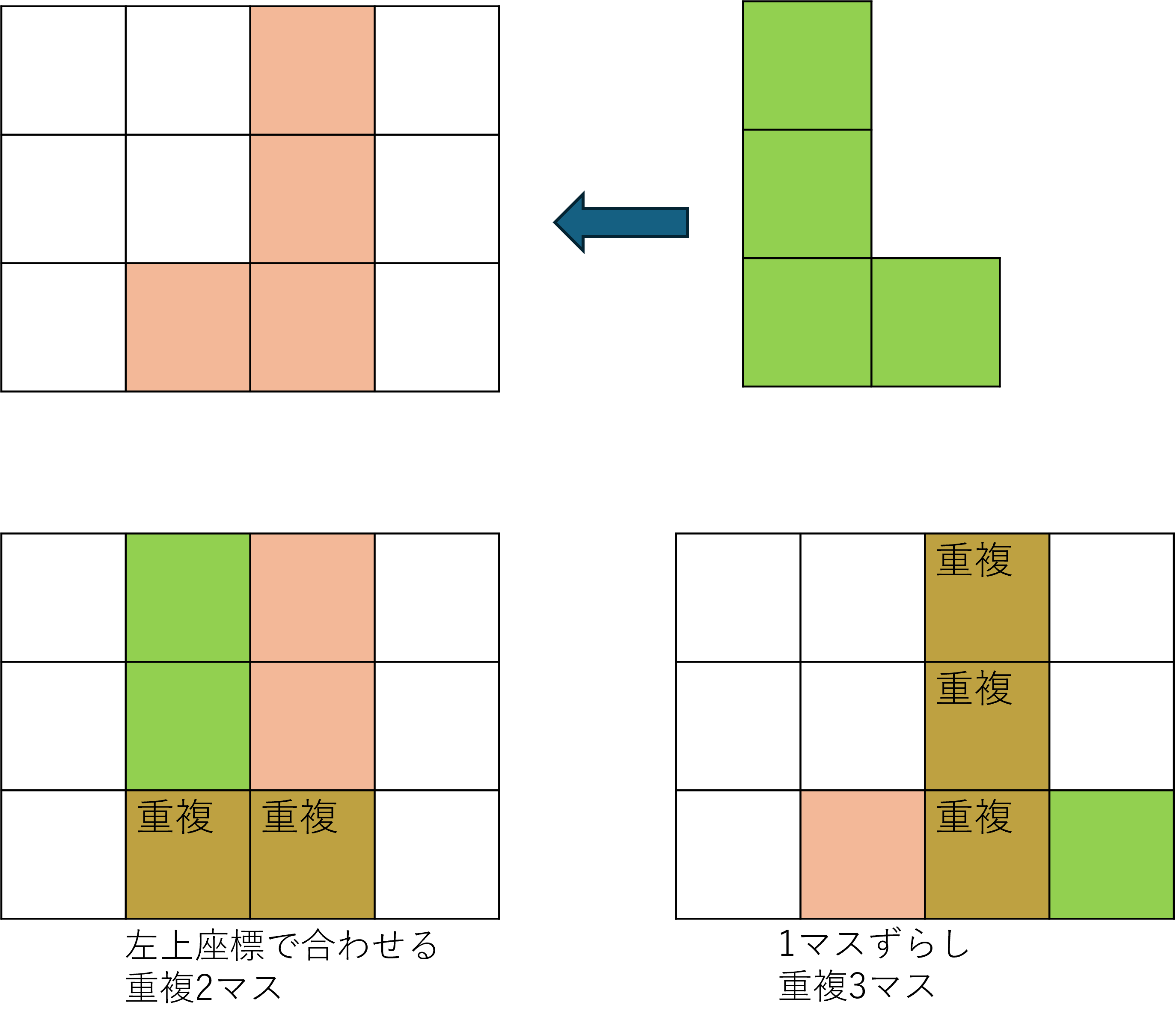
この、「2つの油田を入れ替えたときどれだけずらすか」は、入れ替えタイミングに毎回計算すると時間がもったいないため、油田の形からあらかじめ計算してメモしておきます。
vector<vector<vector<pair<size_t, size_t>>>> get_swaps(const Input &input)
{
// 2つのポリオミノの位置を入れ替える操作を行うために、入れ替えた際にどれだけ位置をずらせばよいかを予め計算しておく
// swaps[oil_id_a][oil_id_b] := oil_id_aとoil_id_b+Δが出来るだけ一致するようなΔ
vector<vector<vector<pair<size_t, size_t>>>> swaps(input.m, vector<vector<pair<size_t, size_t>>>(input.m));
for (size_t oil_id_a = 0; oil_id_a < input.m; ++oil_id_a)
{
const auto &oil_a = input.oils[oil_id_a];
// ポリオミノpを0,0に配置したときの座標ならtrue, それ以外ならfalse
vector<bool> is_a_coordinate(input.n2);
for (size_t ij : oil_a.coordinate_ids)
{
is_a_coordinate[ij] = true;
}
for (size_t oil_id_b = 0; oil_id_b < input.m; ++oil_id_b)
{
const auto &oil_b = input.oils[oil_id_b];
if (oil_id_a == oil_id_b)
{
continue;
}
// 二つのポリオミノが重なっているマスの数と、そのときの位置のずれのリストを計算
std::vector<std::pair<size_t, std::pair<size_t, size_t>>> list;
for (int di = -(int)oil_b.max_i; di <= (int)oil_a.max_i; ++di)
{
for (int dj = -(int)oil_b.max_j; dj <= (int)oil_a.max_j; ++dj)
{
size_t volume = 0;
for (size_t ij : oil_b.coordinate_ids)
{
size_t i = ij / input.n + di;
size_t j = ij % input.n + dj;
if (i >= 0 && j >= 0 && i < input.n && j < input.n && is_a_coordinate[i * input.n + j])
{
++volume;
}
}
list.emplace_back((size_t)volume, make_pair(di, dj));
}
}
// 重なっているマスの数が多い順にソート
sort(list.rbegin(), list.rend());
// 4個である必要はないが、近傍の多様性のために複数持っておく
list.resize(4);
swaps[oil_id_a][oil_id_b].clear();
for (const auto &[volume, i_j] : list)
{
swaps[oil_id_a][oil_id_b].emplace_back(i_j.first, i_j.second);
}
}
}
return swaps;
}
サンプルコード(近傍を工夫した焼きなましで尤度の高いプールを生成)
だいたい当日1位~2位ぐらいのスコアが出せました。
wataさんの元の提出ではこれをはるかに超えるぶっちぎりの1位なのでまだ伸びしろはあると思いますが、いったんスライドに書いてあった工夫はだいたい説明できたと思うので、これで終わりにしたいと思います。
最後に、今回作成したコードの中でM=3以上に対応した3つと、当日6位以内の参加者のコードを用いて100ケースのローカルで相対スコアを出してみました(僕の環境は本番環境より遅そうなので制限時間はとっぱらっています。時間の使い方の工夫の仕方によっては本来の性能にならないかも)。5位のShun_PIさんのコードだけうまく動かせなかったので、除いています。
焼きなましまで到達できれば、近傍を工夫しなくても当日6位ぐらいにはなれそうですね。
| コード(当日順位) | ローカル相対スコア |
|---|---|
| wata(writer) | 7.890321e+11 |
| terry_u16(1th) | 7.163400e+11 |
| 近傍を工夫した焼きなまし | 6.834730e+11 |
| cuthbert(2th) | 6.699114e+11 |
| bowwowforeach(4th) | 6.625972e+11 |
| eijirou(3th) | 6.403401e+11 |
| 焼きなましで尤度の高いプールを生成 | 6.019638e+11 |
| USA(6th) | 4.066429e+11 |
| 数を絞ったランダムなプールを用いる | 2.497436e+11 |
残る課題
wataさんのコードを見る限り、$\epsilon$と$N$の大きさに応じてパラメータや条件分岐を変化させているようでした。
そのまま真似てもよかったんですが、やってることを正確に理解して解説できそうになかったので、今回は$N$だけ使ってかなりシンプルに仕上げました。
このあたりが計算時間を使いきれない理由や、1位になれなかった理由だと思います。
これらについて調べた限りwataさんに負ける理由ではなさそうでしたが、
もしこの記事の内容を全部理解して、もっと工夫したい人がいれば挑戦してみてください。
後日談
ローカルテスト100ケースでちょいちょい時間かクエリのどちらかが足りなくなっていたので、$N$,$M$,$\epsilon$を適当にかけたパラメータをいくつか眺めたところ、$N^2\times M^2\times \epsilon > 2000$ぐらいで失敗しやすそうでした。(残る課題の節で紹介したwataさんのやり方とは異なります)
AtCoderの環境ではTLEは起きてなかったので、難しいケースへの対応よりは簡単なケースについて時間をもうちょい使えそうです。
そこで、簡単なケースのみ探索数を5倍にしたコードを投げてみました。
wataさんには遠く及ばないですが、当日1位に勝てました。
なぜかwaが出てるのでもうちょい調整の余地はあるかもしれません。
最後に
本記事では、AHCの典型解法の1つである、ベイズ推定の具体的な使い方を示しました。
焼きなまし、ビームサーチ、モンテカルロ法といった探索系のアルゴリズムは使える人も増えてきていると思いますが、推定系の問題では何をしたらいいかわからない人も多いと思います。
どうしても数式がいっぱいで上級者向きの印象があるベイズ推定ですが、なるべく1つの記事を読むだけで使い方がわかることを目指しました。
少しでも多くの人がこの記事によってベイズ推定の使い方を理解し、今後のAHCで役立ててくれることを願っています。
サンプルコード5+1種の置き場
-
本来$\mathrm{CDF}$は正規分布に限った用語ではない点と、引数は確率変数$x$だけな点から、丁寧に書くなら$F_{N(\mu,\sigma)}(x)$のように書くべきですが、今回は簡単に$\mathrm{CDF}(x,\mu,\sigma)$と表記します。 ↩
-
$\sum_{x \in \mathcal{X}}$の$\mathcal{X}$のような表記(カリグラフ体)は、確率変数のとりうる値の集合を意味します。記事公開後に修正したため、画像として張り付けている数式には$\sum_{x \in \mathcal{X}}$としたほうが適切な部分で、$\sum_{x \in X}$のようにカリグラフ体になっていない部分が残っています。ご了承ください。 ↩



