相互情報量を学んでもっとうまくAHC030を解こう！

前回記事の振り返り

前回記事ではAHC030のseed0をベイズ推定を用いて解く方法について説明しました。この内容を前提とするので読んでない方はぜひ読んでみてください。

ベイズ推定を使ってかなり賢く解くことはできましたが、まだまだ改善の余地はあります。特に、点集合をランダムに選んでいましたが、この部分をうまく選べばさらに効率的に特定することができます。今回はその具体的方法と実装について説明していきます。

注意

前回の内容は実際のコンテストで私自身が実際に使い、効力を感じたことに基づいて書きましたが、今回の内容はコンテスト後に学んだことです。そのため、本当にコンテストで有効かどうかを検証したわけではないことをご了承ください。

相互情報量を最大化する！

今回はうまく点集合を選ぶことを目標としますが、そのためにはどのような選び方が"うまい"選び方なのかということを定義する必要があります。私はコンテスト中この部分がよくわからず、自己流でそれっぽいロジックを適当に実装したのですが、コンテスト後に最終1位のterryさんやwriterのwataさんの言及によると、相互情報量なる概念を最大化するような選び方をすればよいらしいです。
そこで、今回は相互情報量を最大化するような選び方をするということは具体的にどのようなことなのかを学び、実装して効力を検証しようと思います。(相互情報量を最大化するのがよいということについては証明せず、信じることにします)

相互情報量

相互情報量$I$の定義をwikipediaから引っ張ってきた式です。

I(X, Y) = \sum_{x \in X} \sum_{y \in Y} P(x,\ y) \log \frac{P(x,\ y)}{P(x)P(y)}

この式を見て、「あーはいはい、完全に理解したわ。実装します」となる人はこの記事を読まないと思うので、まずはこの式の意味について考えていきましょう。

前回と同じように、可能な盤面をすべて列挙した列を$B_1,\ B_2,\ ...\ ,\ B_n$、$i$回目のクエリの前の各盤面の確率を$P_{i,\ 1},\ P_{i,\ 2},\ ...\ ,\ P_{i,\ n}$と置くことにしましょう。
ここで、前回は乱択で適当に$i$回目のクエリを投げていましたが、クエリで選択する点集合$S$に対して相互情報量$I$を求め、$I$を評価値としてなるべくよいクエリを選択することにします。(実際にはクエリのcost$c$も考慮して、$I/c$を評価値とします)

上の式で言う$X$は盤面の集合$B$のことで、$Y$というのはクエリの結果の集合$R$だと思ってください。
そうすると、上の式は全ての$B_j$とクエリの結果$res$の組合わせに対して、$P(B_j,\ res) \log \frac{P(B_j,\ res)}{P(B_j)P(res)} $を計算して足し合わせるという意味になります。

ここでの$P(B_j,\ res)$は前回出てきた$P(res|B_j)$とは異なるものであることに注意してください。$P(res|B_j)$は盤面が$B_j$であることを仮定したうえでの確率ですが、$P(B_j,\ res)$はその仮定をしていません。$P(B_j\cap res)$と書くほうが分かりやすいと思うので、そう書くことにします。

条件付確率の有名な公式として、$P(A|B) = P(A\cap B)/P(B)$というものがあります。つまり$P(A\cap B) = P(A| B)\times P(B)$であるということなので、この式を使うと、

\begin{align}
P(B_j,\ res) \log \frac{P(B_j,\ res)}{P(B_j)P(res)} &= P(B_j\cap res) \log \frac{P(B_j\cap res)}{P(B_j)P(res)}\\
& = P(res|B_j)P(B_j)\log \frac{P(res|B_j)P(B_j)}{P(B_j)P(res)}\\
& =  P(res|B_j)P(B_j)\log \frac{P(res|B_j)}{P(res)}
\end{align}

というふうに式変形できます。この式の中で、$P(B_j)$は$B_j$の事前確率$P_{i,\ j}$ですし、$P(res|B_j)$は前回の記事で議論した尤度と同じものです。ということは、$P(res)$が求まれば相互情報量$I$は計算できるということになります。

$P(res)$、つまり点集合Sについてのクエリの結果が$res$となる確率ですが、これは結論から言うと$\sum_j P(B_j)P(res|B_j)$として求められます。(式変形も示しておきます。)これを前計算しておくことで$I$を計算できそうです。

\begin{align}
P(res) &= \sum_j P(B_j\cap res) \\
& =\sum_j P(B_j)P(res|B_j)\\
\end{align}

式を追うだけでもなかなか大変なんじゃないかと思います。やはりここまでくるとなかなか難しいです。しかし、例によって実装を見るとわかりやすいかもしれませんので、あきらめずに実装を見てみるといいかもしれません。

実装

前回記事のコードを前提とします。前回点集合を乱択していた部分を、よりよい点集合を探索する関数によってえらばれた点集合に変更します。この関数では、点を乱択して、その点が点集合に含まれる/含まれないを変更することで相互情報量/costが改善するなら採用するという山登り法によって点集合を選択します。

// 盤面の点をランダムに選び、setに入れる/入れないで相互情報量が多くなる場合のみ採用する乱択山登り
vector<pair<int, int>> decide_set(vector<vector<vector<int>>> &candidates,
                                  vector<double> &p) {
    int n = candidates.size();

    // b[i][j]がtrueならsetに入っていることを表す。最初は全点入れる
    vector<vector<bool>> b(N, vector(N, true));
    int k = N * N;
    double best_mi = 0.0;

    // i番目の盤面のv(S)の値
    vector<int> cnt(n);
    rep(i, 0, n) {
        rep(j, 0, M) cnt[i] += V[j].size();
    }

    // 点を乱択し、setに入れる/入れないを変更する。相互情報量/costが増えるなら採用
    rep(t, 0, 1000) {
        int x = rnd(N);
        int y = rnd(N);
        int delta = b[x][y] ? -1 : 1;

        rep(i, 0, n) cnt[i] += candidates[i][x][y] * delta;
        k += delta;

        // 更新していたら採用
        if(chmax(best_mi, mutual_information(p, cnt, k))) {
            b[x][y] = b[x][y] ^ 1;
            continue;
        }

        // 採用しない場合は元に戻す
        delta *= -1;
        rep(i, 0, n) cnt[i] += candidates[i][x][y] * delta;
        k += delta;
    }

    vector<pair<int, int>> res;
    rep(i, 0, N) rep(j, 0, N) if(b[i][j]) res.push_back({i, j});

    return res;
}

相互計算量を計算しているパートです。まず式変形のところで出てきた$P(res)$を計算しておき、その結果を使って$P(res|B_j)P(B_j)\log \frac{P(res|B_j)}{P(res)}$をすべての$res,j$の組に対して計算し、足していっています。最後にcostで割ります。

// 相互情報量/costを計算
double mutual_information(vector<double> &p, vector<int> &cnt, int k) {
    int n = p.size();

    // 現在の確率分布の下で、結果がresとなる確率を計算
    vector<double> res_p(300);
    rep(i, 0, n) {
        // 高速化のため、確率が高いところだけ見ることにする(非本質ですが、全部見ると時間がかかるので)
        if(p[i] < 1e-5) continue;
        int m = (k - cnt[i]) * EPS + cnt[i] * (1 - EPS);
        rep(res, m, 300) {
            auto d = likelihood(k, cnt[i], res);
            if(d < 1e-3) break;
            res_p[res] += d * p[i];
        }

        for(int res = m - 1; res >= 0; res--) {
            auto d = likelihood(k, cnt[i], res);
            if(d < 1e-3) break;
            res_p[res] += d * p[i];
        }
    }

    double mi = 0;
    rep(res, 0, 300) {
        // ここも確率が高いところだけみる
        if(res_p[res] < 1e-3) continue;
        rep(i, 0, n) {
            if(p[i] < 1e-5) continue;

            double p_res_i = likelihood(k, cnt[i], res);
            if(p_res_i > 0.0) mi += p[i] * p_res_i * log(p_res_i / res_p[res]);
        }
    }

    return mi * sqrt(k);
}

全体のコードです。細部をやや変更しましたが、基本的に点集合を選んでいるところ以外は同じようなことをしています。これでどれほど改善するのでしょうか。

#include <bits/stdc++.h>
using namespace std;

#define rep(i, a, b) for(int i = a; i < (int)b; i++)

template <class T, class S>
bool chmax(T &a, const S &b) {
    if(a < (T)b) {
        a = (T)b;
        return 1;
    }
    return 0;
}
template <class T, class S>
bool chmin(T &a, const S &b) {
    if((T)b < a) {
        a = (T)b;
        return 1;
    }
    return 0;
}

// 乱数生成器
struct RandomNumberGenerator {
    mt19937 mt;

    RandomNumberGenerator()
        : mt(chrono::steady_clock::now().time_since_epoch().count()) {}

    int operator()(int a, int b) {  // [a, b)
        uniform_int_distribution<int> dist(a, b - 1);
        return dist(mt);
    }

    int operator()(int b) {  // [0, b)
        return (*this)(0, b);
    }
} rnd;

// 正規分布の累積分布関数
constexpr double normal_cdf(double x, double mean = 0.0, double sigma = 1.0) {
    return 0.5 * (1.0 + std::erf((x - mean) / (sigma * 1.41421356237)));
}
constexpr double probability_in_range(double l, double r, double mean = 0.0,
                                      double sigma = 1.0) {
    assert(l <= r);
    if(mean < l)
        return probability_in_range(2.0 * mean - r, 2.0 * mean - l, mean,
                                    sigma);
    double p_l = normal_cdf(l, mean, sigma);
    double p_r = normal_cdf(r, mean, sigma);
    return p_r - p_l;
}

void normalize(vector<double> &v) {
    double s = 0;
    for(auto d : v) {
        s += d;
    }
    assert(s > 0);

    for(auto &d : v) {
        d /= s;
    }
}

// 質問query
int query(vector<pair<int, int>> v) {
    cout << "q"
         << " " << v.size() << ' ';
    for(auto [x, y] : v) {
        cout << x << ' ' << y << ' ';
    }

    cout << endl;

    int res;
    cin >> res;
    return res;
};

// 解答query
int answer(vector<pair<int, int>> v) {
    cout << "a"
         << " " << v.size() << ' ';
    for(auto [x, y] : v) {
        cout << x << ' ' << y << ' ';
    }

    cout << endl;

    int res;
    cin >> res;
    return res;
}

int N, M;
double EPS;
vector<vector<pair<int, int>>> V;
vector<int> x_max;
vector<int> y_max;

//  入力を受け取る。ついでに各ポリオミノの縦横の大きさも
void input() {
    cin >> N >> M >> EPS;
    V.resize(M);
    x_max.resize(M);
    y_max.resize(M);

    rep(i, 0, M) {
        int k;
        cin >> k;
        V[i].resize(k);
        rep(j, 0, k) {
            int x, y;
            cin >> x >> y;
            V[i][j] = {x, y};
            chmax(x_max[i], x);
            chmax(y_max[i], y);
        }
    }
}

// 個数k, v(S) = cntの点集合からresが得られたときの尤度(条件付き確率)
double likelihood(int k, int cnt, int res) {
    double mean = (k - cnt) * EPS + cnt * (1 - EPS);
    double sigma = sqrt(k * EPS * (1 - EPS));

    if(res == 0) return probability_in_range(-1e10, res + 0.5, mean, sigma);
    return probability_in_range(res - 0.5, res + 0.5, mean, sigma);
}

// bfsで可能なすべての盤面を生成。Mが大きいときはTLE
vector<vector<vector<int>>> make_all_candidates() {
    vector<vector<vector<int>>> q;
    q.push_back(vector(N, vector(N, 0)));

    rep(i, 0, M) {
        vector<vector<vector<int>>> nq;
        for(auto b : q) {
            rep(j, 0, N - x_max[i]) rep(k, 0, N - y_max[i]) {
                auto nb = b;
                for(auto [x, y] : V[i]) {
                    nb[j + x][y + k]++;
                }
                nq.push_back(nb);
            }
        }

        swap(nq, q);
    }

    return q;
}

// 相互情報量/costを計算
double mutual_information(vector<double> &p, vector<int> &cnt, int k) {
    int n = p.size();

    // 現在の確率分布の下で、結果がresとなる確率を計算
    vector<double> res_p(300);
    rep(i, 0, n) {
        // 高速化のため、確率が高いところだけ見ることにする(非本質ですが、全部見ると時間がかかるので)
        if(p[i] < 1e-5) continue;
        int m = (k - cnt[i]) * EPS + cnt[i] * (1 - EPS);
        rep(res, m, 300) {
            auto d = likelihood(k, cnt[i], res);
            if(d < 1e-3) break;
            res_p[res] += d * p[i];
        }

        for(int res = m - 1; res >= 0; res--) {
            auto d = likelihood(k, cnt[i], res);
            if(d < 1e-3) break;
            res_p[res] += d * p[i];
        }
    }

    double mi = 0;
    rep(res, 0, 300) {
        // ここも確率が高いところだけみる
        if(res_p[res] < 1e-3) continue;
        rep(i, 0, n) {
            if(p[i] < 1e-5) continue;

            double p_res_i = likelihood(k, cnt[i], res);
            if(p_res_i > 0.0) mi += p[i] * p_res_i * log(p_res_i / res_p[res]);
        }
    }

    return mi * sqrt(k);
}

// 盤面の点をランダムに選び、setに入れる/入れないで相互情報量が多くなる場合のみ採用する乱択山登り
vector<pair<int, int>> decide_set(vector<vector<vector<int>>> &candidates,
                                  vector<double> &p) {
    int n = candidates.size();

    // b[i][j]がtrueならsetに入っていることを表す。最初は全点入れる
    vector<vector<bool>> b(N, vector(N, true));
    int k = N * N;
    double best_mi = 0.0;

    // i番目の盤面のv(S)の値
    vector<int> cnt(n);
    rep(i, 0, n) {
        rep(j, 0, M) cnt[i] += V[j].size();
    }

    // 点を乱択し、setに入れる/入れないを変更する。相互情報量/costが増えるなら採用
    rep(t, 0, 1000) {
        int x = rnd(N);
        int y = rnd(N);
        int delta = b[x][y] ? -1 : 1;

        rep(i, 0, n) cnt[i] += candidates[i][x][y] * delta;
        k += delta;

        // 更新していたら採用
        if(chmax(best_mi, mutual_information(p, cnt, k))) {
            b[x][y] = b[x][y] ^ 1;
            continue;
        }

        // 採用しない場合は元に戻す
        delta *= -1;
        rep(i, 0, n) cnt[i] += candidates[i][x][y] * delta;
        k += delta;
    }

    vector<pair<int, int>> res;
    rep(i, 0, N) rep(j, 0, N) if(b[i][j]) res.push_back({i, j});

    return res;
}

// ベイズ推定をする
void bayesian_inference(vector<vector<vector<int>>> candidates) {
    int n = candidates.size();

    // 初期確率は全て等しい
    vector<double> p(n, 1.0 / n);

    bool success = 0;
    while(!success) {
        // 相互情報量がなるべく多いsetを選ぶ。前回記事からの更新
        auto v = decide_set(candidates, p);
        int k = v.size();

        // 点集合についてqueryを投げる
        int res = query(v);

        rep(i, 0, n) {
            // i番目の盤面を仮定したときのv(S)の値を取得
            int cnt = 0;
            for(auto [x, y] : v) {
                cnt += candidates[i][x][y];
            }

            // 事前確率に尤度を掛ける
            p[i] *= likelihood(k, cnt, res);
        }

        normalize(p);

        while(1) {
            // 80%以上の確率で正解できそうなら聞いてみる
            auto max_it = max_element(p.begin(), p.end());
            int max_ind = max_it - p.begin();

            if(*max_it < 0.8) break;

            vector<pair<int, int>> v;
            rep(i, 0, N) rep(j, 0, N) {
                if(candidates[max_ind][i][j] > 0) v.push_back({i, j});
            }

            // 正解なら終了。だめならその事前確率を0にして継続
            success = answer(v);
            if(success)
                break;
            else {
                p[max_ind] = 0.0;
                normalize(p);
            }
        }
    }
}

int main() {
    input();

    bayesian_inference(make_all_candidates());
}

結果

結果はこのようになりました。costは0.38ほどであり、1.8ほどかかっていた前回に比べ相当改善したことが分かります。特に最後の質問クエリでは明確に境界付近を狙って聞いていることから、より情報の価値の高い集合が選ばれている雰囲気が分かると思います。

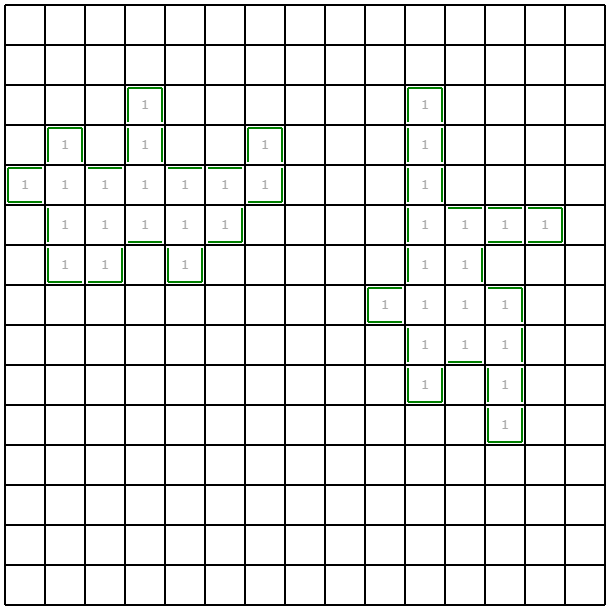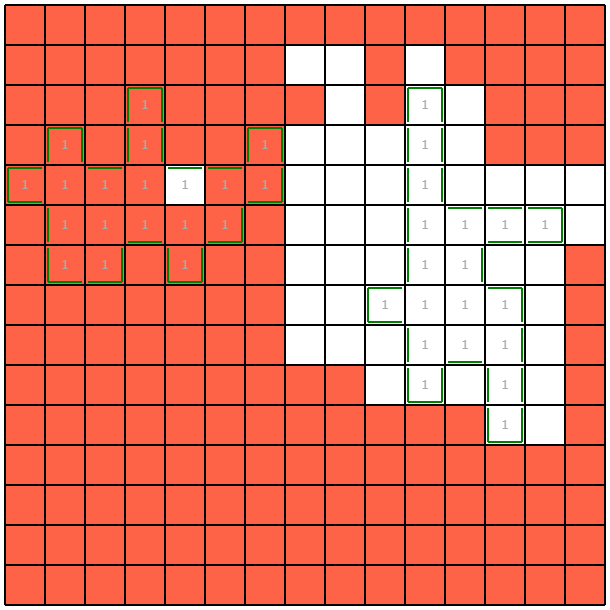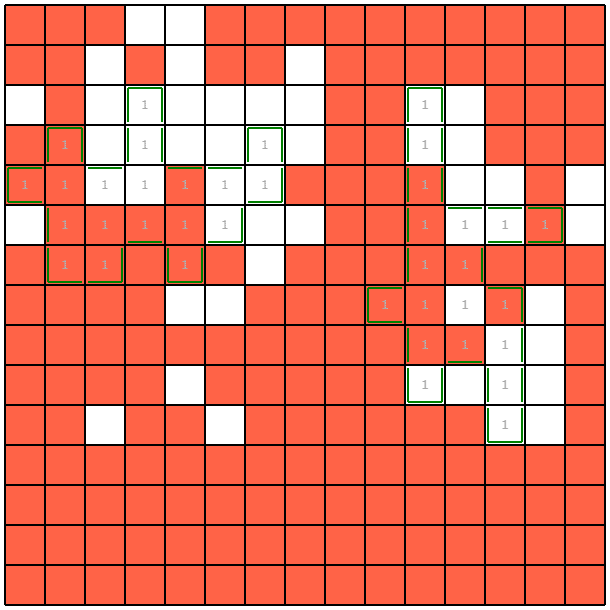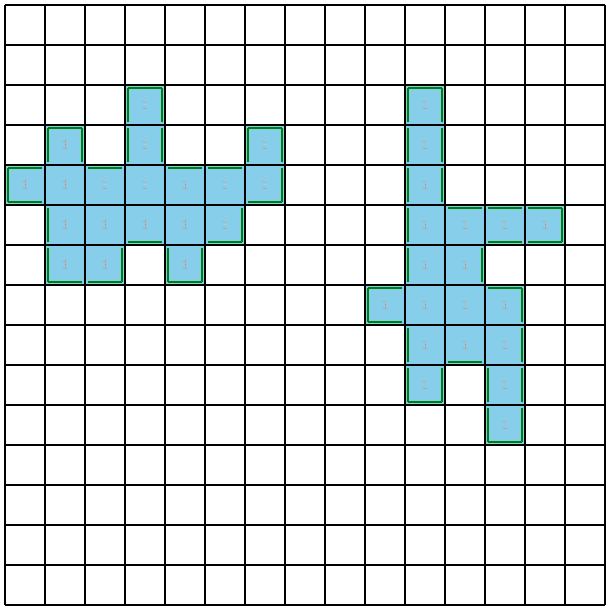
実行時間がかかりすぎていることについて

今回、私のローカルでの実験では数十秒の実行時間を要しました。相互情報量の計算では盤面集合$B$とクエリ結果の集合$R$の二重でループを回さざるを得ず、ナイーブな実装ではどうしても実行時間がかかってしまいます。
これをどうやってTL内に収めるのかは、読者に委ねたいと思います。(他力本願)

最後に

式変形もかなり複雑になってしまったうえ、最後はTLに間に合わないという結果になってしまいました。そんなにいい記事である自信がないのですが、参考になれば幸いです。

感想や間違いの指摘をお待ちしております。