LoginSignup
13
9

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@thun-c(thunder)

AHC典型解法シリーズ第4弾「ビームサーチ」

Posted at

はじめに

本記事では、AHCの過去問のネタバレを多く含みます。自力で一から試す腕試しをしたい場合は注意してください。

本記事はAHC典型解法をまとめたシリーズ記事の第4段です。
シリーズ全体の目的や方針は第1段を参照ください。

これまでのシリーズ記事

本記事シリーズを紹介します。
一部、他に参考となりそうな記事も紹介しています。

大カテゴリ 小カテゴリ 記事名(URL) 執筆済み
典型手法 モンテカルロ法 AHC典型解法シリーズ第1弾「モンテカルロ法」 済
典型手法 焼きなまし法(山登り法含む) AHC典型解法シリーズ第2弾「焼きなまし法」 済
典型手法 ベイズ推定 AHC典型解法シリーズ第3弾「ベイズ推定」 済
典型手法 ビームサーチ (焼きなましとの合わせ技含む) AHC典型解法シリーズ第4弾「ビームサーチ」 本記事
典型手法 天才 代替記事：焼きなまし法が使えなくても AHC 橙になれたよ(Kiri8128) 　執筆予定なし
集計 解法まとめ ahcまとめ(thunder) 古い
全般の進め方 基本的なローカルテスト AHC初心者向け、ローカルテスタの使い方 済
全般の進め方 並列ローカルテスト 代替記事：【競プロ】テスト10倍速！AtCoder AHC向け【Python】自動テスト並列処理ツール(toast-uz)

代替記事：Pahcer(terry_u16) 		執筆予定なし

典型手法「ビームサーチ」とAHC041

今回はビームサーチの例題としてAHC041を扱います。
この問題は、writerが「焼きなまし系の問題」として想定していた1にもかかわらず、1位解法がビームサーチだった異様な回です。
SNSを見ていると、AHCについて、「焼きなまし法やビームサーチを知らないと戦えない」、「焼きなまし法の問題だから焼きなまし法を使わないといけない」、「焼きなまし法やビームサーチさえ使えれば上位になれる」と思っている方をちらほら見かけます。
本記事含め、「AHC典型解法シリーズ」がこの風潮を増長させるきっかけになってしまっているかもしれません。
今回は典型解法としてビームサーチを扱いますが、「ただビームサーチを使えばいい」とならないよう、失敗例も含めて解説します。
この解説を通して、以下のポイントを抑えることを目標とします。

  • 典型解法を使う「だけ」ではなく、「その問題をどう解くか考える」ことが重要
  • 扱う1手の進ませ方が同じであれば、貪欲法よりもビームサーチのほうが良い可能性が高い2
  • 扱う1手の進ませ方が異なれば、ビームサーチが貪欲法に負けることもある
手法 順位(当日相当)
なにもしない 954位 提出リンク
順番にBFS 741位 提出リンク
BFSする根の順序を貪欲に選ぶ 689位 提出リンク
BFSする根の順序をビームサーチで選ぶ 664位 提出リンク
木を焼きなます 291位 提出リンク
深さを低い順に選ぶ 19位 提出リンク
深さをビームサーチで選ぶ 1位 提出リンク
深さをビームサーチで選ぶ（いろいろ工夫） 1位 提出リンク
深さをビームサーチで選んだ後に焼きなます 1位（既に抜かれたが、提出時点では延長戦でも1位）提出リンク

それぞれのサンプルコードはこちらにまとめています。

AHC041の問題設定

この問題は、正の整数をとる美しさを持つ連結な頂点と、向きを持たない辺からなるグラフがが与えられ、見栄えが最大化されるように根付き木の集合ををつくる問題です。

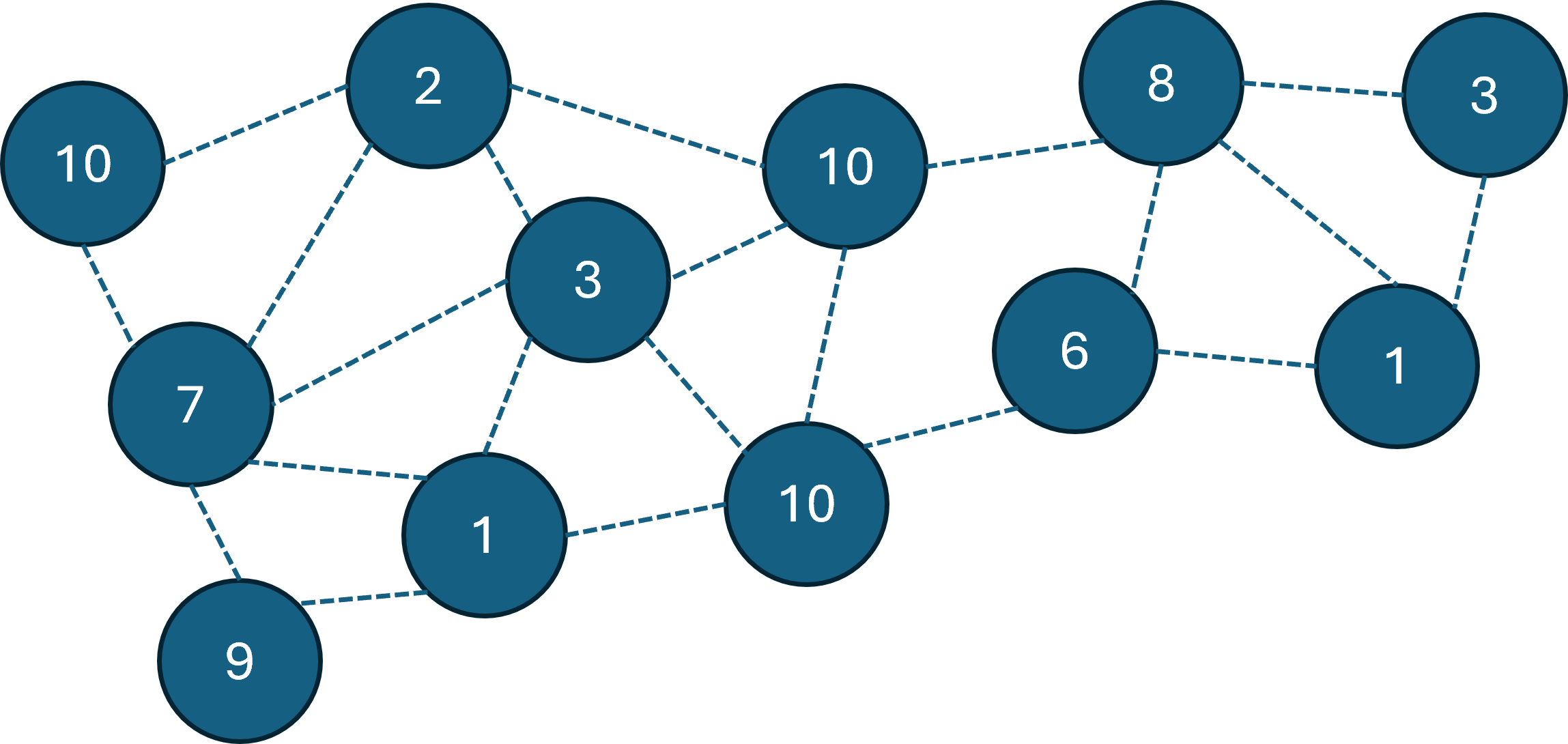
たとえば、以下のようなグラフが与えられます。本来は頂点が1000個ありますが、簡単のために小さいグラフで説明します。ここでは、各頂点に記載されちる数を美しさとします。

00_shoki.png

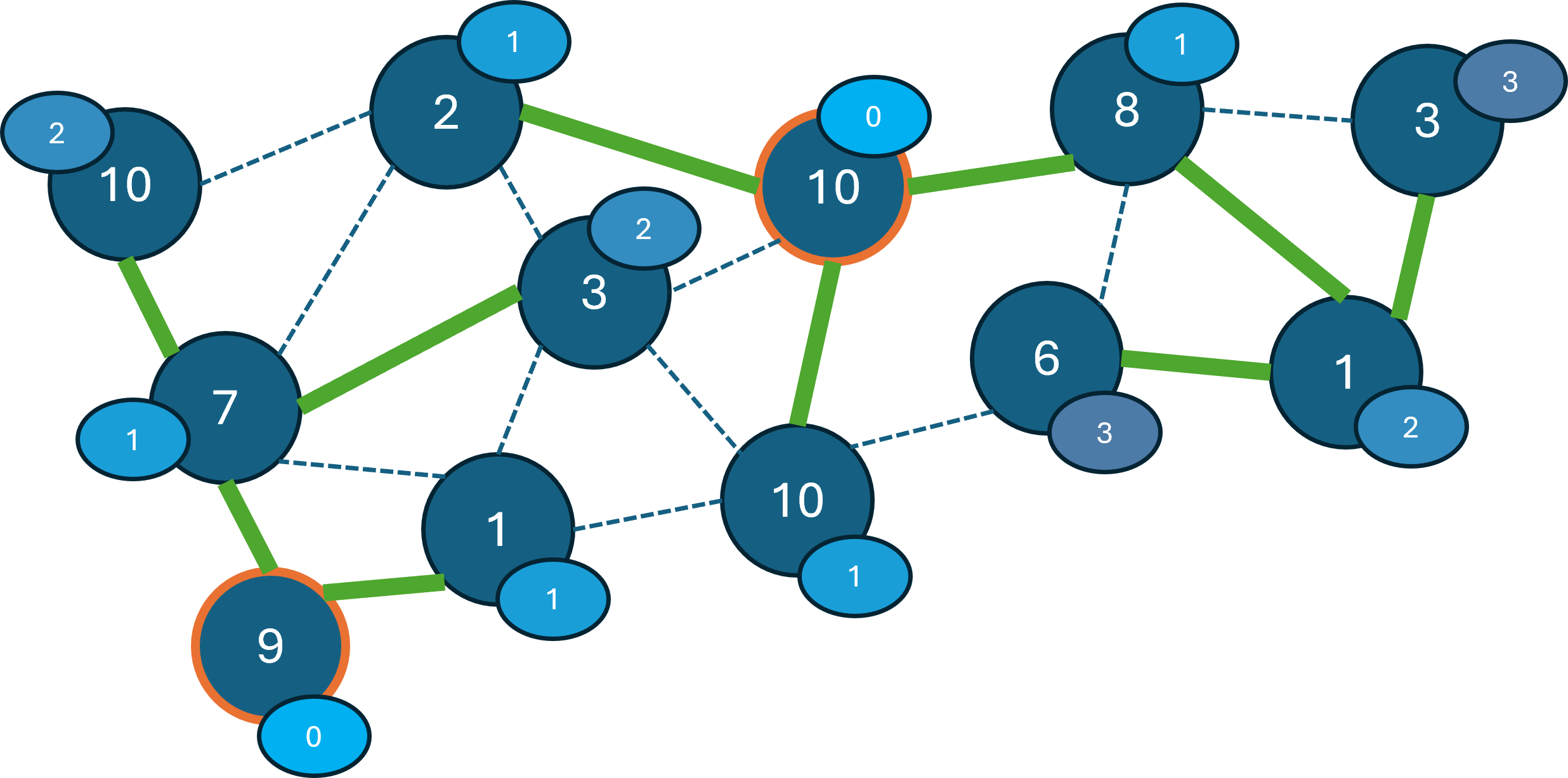
ここで、以下のようにオレンジの枠をつけた2つの頂点を根とする木をつくった場合の見栄えの計算方法を説明します。
見栄えは、$(各頂点の高さ+1) \times (各頂点の美しさ)の総和+1$で計算されます。
きれいさ9の頂点を根とした木については、
$9\times 1 + 1\times 2 + 7\times 2 + 3\times 3 +10\times 3 = 40$
きれいさ10の頂点を根とした木については、
$10\times 1 + 10\times 2 + 2\times 2 + 8\times 2 +1\times 3 + 3 \times 4 + 6 \times 4 = 89$
となるため、
全体の見栄えは$1+40+89=130$となります。
この値を大きくすることが問題の目的です。

なお、問題文の定義では今のように最後に1を足すのですが、どの解でも平等に1を足すことになるため、本記事では以降、1を足さないスコアで説明します。

01_sample.png

なお、根付き木というのは、ある特別な1つの頂点（根）を持ち、根からの深さ（高さ）を持つ木のことです。
木というのは閉路を持たない連結なグラフのことです。
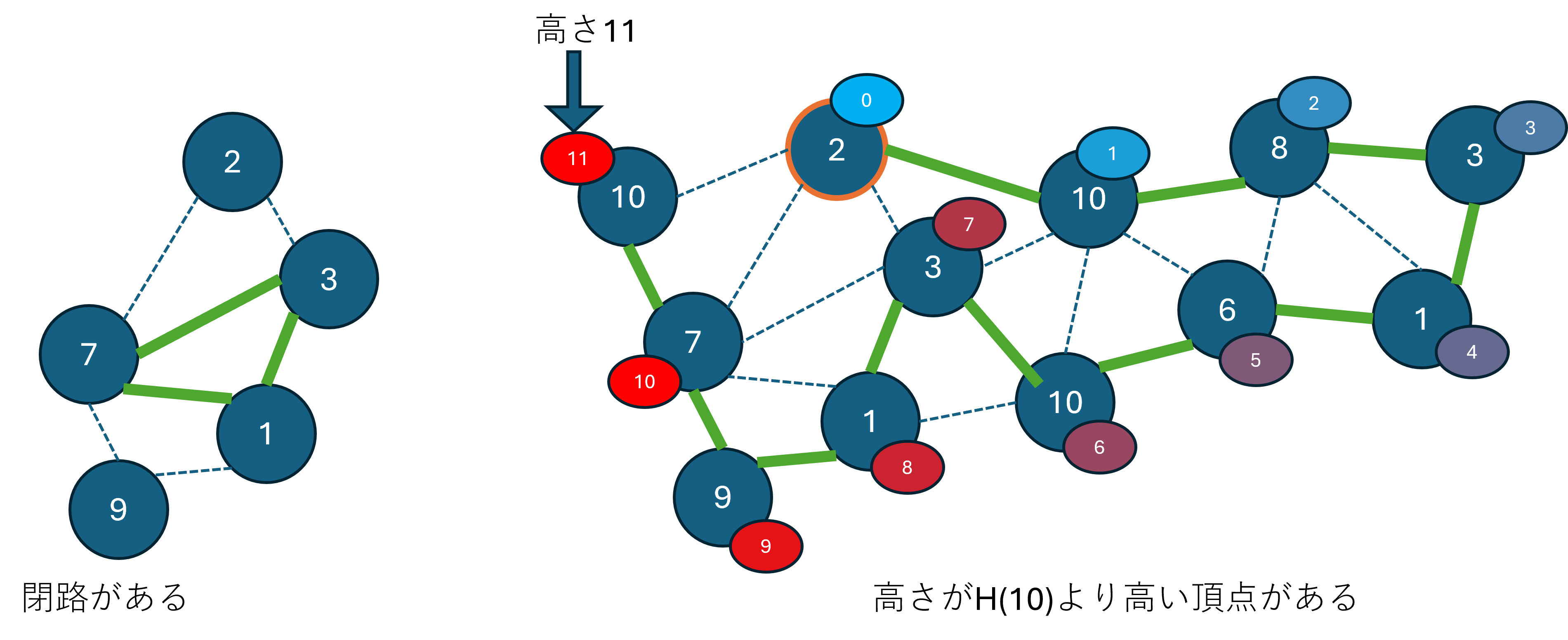
たとえば、以下の左図のように、辺を辿ると同じ頂点に戻るような道があるグラフは木ではありません。
また、今回の問題では、高さが最大H(=10)以下であるという制約があります。
そのため、以下の右図のように、高さ11となる頂点を持つ木をつくることはできません。

02_ng.png

なにもしない

手法説明

まずは提出してスコアを獲得できるコードをつくってみましょう。
1頂点だけでも根付き木の条件を満たすので、とりあえず全頂点を1頂点ずつの根付き木として見なせば、解を出すことができます。

03_none.png

実装説明

この問題では、N個の頂点の親の頂点を出力することが求められています。
根には親がないため、代わりに-1を出力します。

今回は全頂点を根とするため、単にN回-1を出力すればよいです。

00_none.cpp
// include文等の説明aは省略

/// @brief 各頂点の親を出力
/// @param answer 頂点iの親の頂点
void output(vector<int> &answer)
{
    for (int i = 0; i < N; i++)
        cout << answer[i] << " ";
    cout << endl;
}

int main()
{
    input(); // 入力 実装部分の説明は省略
    vector<int> parents(N, -1);
    output(parents);
}

これでいったんスコアを獲得できました。

手法 スコア 順位(当日相当)
なにもしない 7584268 954位 提出リンク

順番にBFS

手法説明

それでは、根以外の頂点も含めた木をつくってみましょう。
ここでは、BFS(幅優先探索の英語名の略称)を用いて木をつくることを考えます。

まず、どれか1つの頂点を選択し、隣接する頂点全てに辺を伸ばします。
今辺を伸ばした頂点の高さがH未満の場合、そこからまた隣接する頂点全てに辺を伸ばします。
これを繰り返し、伸ばせる頂点がなくなったら終了します。
本来H=10ですが、簡単のために本記事では以降、H=2で説明します。

04_bfs1.png

1本の木では全頂点をカバーできないため、まだ木に含めていない頂点があれば、そこから木をつくるのを繰り返します。
この例では、2本の木で全頂点を覆うことができました。
なにもしない場合と比べ、深さ1以上の頂点が増え、大幅にスコアが伸びました。

04_bfs2.png

AHCでは、グラフを扱う問題や、グラフと見なせる問題が多いため、BFSと、その対となるDFS(深さ優先探索の英語名の略称)はよく使うので覚えておきましょう。

実装説明

指定した頂点root_iを根として探索する関数bfsを実装します。
各頂点の親を記録する配列をN個用意し、まだどの木にも属していない頂点は-2として初期化します。-2はなんでもいいですが、問題文で指定されている-1と、N以下の正の整数は既に意味を持つ値なので、それ以外の整数として-2を用いました。
難しければ、木に属すかどうかを記録するbool配列をもうひとつ用意する実装方法でもよいです。

01_tree_rule.cpp
    /// @brief 状態
    struct State
    {
        vector<int> parents; // 各頂点の親の頂点。-1は根、-2は未確定
        State() : parents(N, -2)
        {
        }

        void bfs(int root_i)
        {
            if (parents[root_i] != -2)
                return;
            queue<pair<int, int>> q;
            parents[root_i] = -1;
            q.push({0, root_i});
            while (!q.empty())
            {
                auto [d, parent] = q.front();
                q.pop();
                for (auto &&child : G[parent])
                {
                    if (parents[child] == -2 && d < H)
                    {
                        parents[child] = parent;
                        q.push({d + 1, child});
                    }
                }
            }
        }
    };

あとは、今つくったbfs関数を用いて全頂点を順番に根とた木をつくればよいです。
なお、先述のbfs関数の冒頭でif (parents[root_i] != -2) return;という処理を入れているので、指定した頂点が既に根付き木に属している場合は何もしません。
ここでは実装していませんが、これまでに木に属した頂点数を記録しておけば、ループをN回まわす前に終了することも可能です。

01_tree_rule.cpp
struct Rule
{
    /// @brief ルールに従って行動を決定する
    /// @param state 初期状態
    /// @return 最も良い最終状態
    State solve(const State &state)
    {
        State now_state = state;
        for (int i = 0; i < N; i++)
            now_state.bfs(i);
        return now_state;
    }

    /// @brief ルールに従って解を求め、必要な情報を抜き出して出力する
    vector<int> getAnswer()
    {
        State best_state = solve(State());
        return best_state.parents;
    }
};

なにもしない場合と比べて文字通り桁違いのスコアがでました。

手法 スコア 順位(当日相当)
なにもしない 7584268 954位 提出リンク
順番にBFS 55988632 741位 提出リンク

BFSする根の順序を貪欲に選ぶ

手法説明

先ほどの解法では、根にする頂点をなんの指標もなく選択して順番に木をつくっていました。
ここで、木を1本構築するごとに、残る全ての頂点の中から、どの頂点を根とするのがいいか比較することを考えます。
今回は、構築予定の木を加えたときのスコア合計が最大になる頂点を根とします。
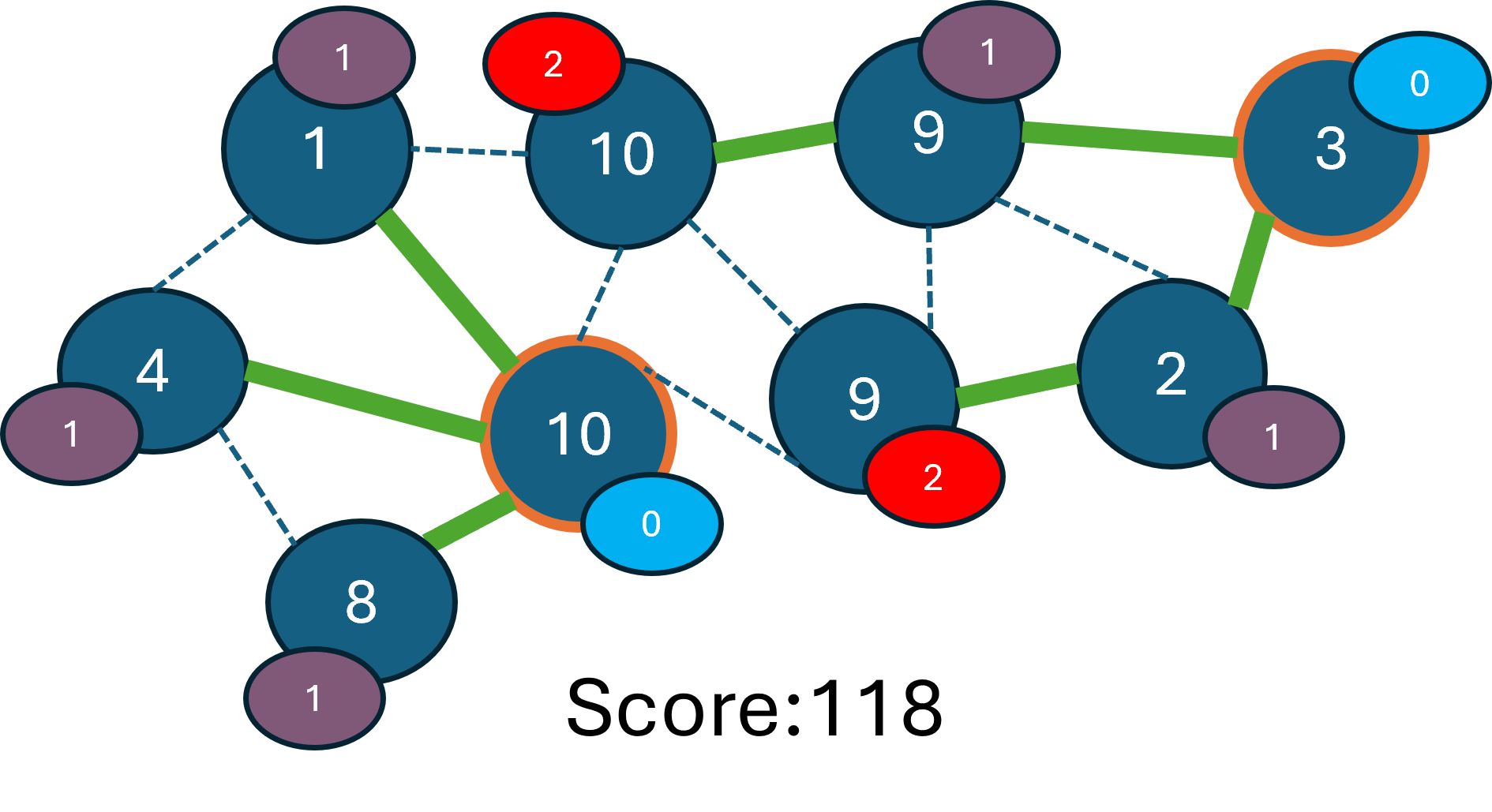
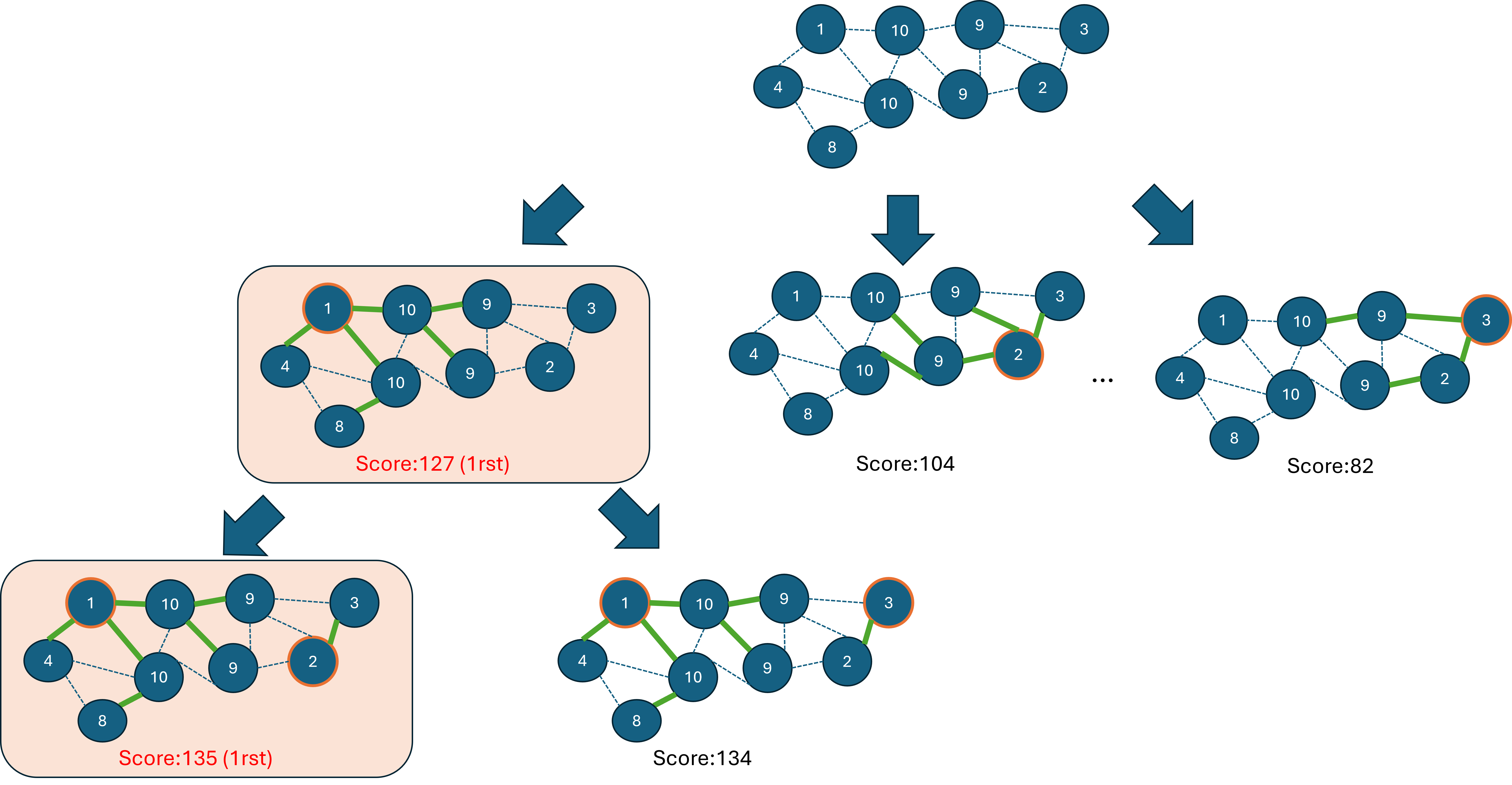
図のように、1本目の木をを構築する時点ではきれいさ1の頂点を根とする木を加えるとスコア合計が127で最大です。
この1本目の木がある状態で、残る全ての頂点の中から、構築できる木を加えたときのスコア合計が最大になる木を加えます。
この時点では、きれいさ2の頂点を根とする木を加えるとスコア合計が135で最大です。
このように、解の一部を構築した時点のスコアが最大となる部分解から、徐々に解を構築していくことを貪欲法(greedy)といいます。

05_tree_greedy.png

実装説明

部分解をもつ状態を表すStateに、スコアを記録するメンバ変数を追加し、bfs関数中にスコアを計算する処理を追加します。
深さdの頂点の隣接点に辺を伸ばす際、子頂点の深さはd+1となるため、スコア計算時にかける重みはd+1+1=d+2となる点に注意してください。
また、新しい解候補のリストに1つ候補を追加するための関数expandを実装します。
ここでは、各頂点を根とした木を追加した場合のStateをnext_statesに追加します。
以下では実装していないですが、追加済みの頂点については、bfs関数を呼び出す前にcontinueしてもいいです。

02_tree_greedy.cpp

    /// @brief 状態
    struct State
    {
        ScoreType score;
        vector<int> parents; // 各頂点の親の頂点。-1は根、-2は未確定

        void bfs(int root_i)
        {
            // ~~省略~~
            
            q.push({0, root_i});
            score += A[root_i]; // 根の頂点の美しさをスコアに加算
            // ~~省略~~

                    if (parents[child] == -2 && d < H)
                    {
                         // 追加する子頂点は高さがd+1なので、きれいさにd+1+1=d+2をかける
                        score += A[child] * (d + 2);
                        parents[child] = parent;
                        q.push({d + 1, child});
                    }
            // ~~省略~~
        }

        
        /// @brief 現在の状態から、次の状態リストを作る
        /// @param next_states 次の状態
        void expand(
            vector<State> &next_states) const
        {
            for (int i = 0; i < N; i++)
            {
                State ps = *this;
                ps.bfs(i);
                next_states.push_back(ps);
            }
        }
    };

今実装したexpand関数を用いて、次のステップの解候補next_statesを作ります。
その後、next_statesの中から、スコアが最大のものを選択します。
全ての頂点を使い終わっていたら終了します。

なお、拙作「ゲームで学ぶ探索アルゴリズム実践入門」の貪欲法の実装では行動リストを作成するleagalActions関数と行動を元に状態を更新するadvance関数を実装していましたが、本記事の後半で行う処理で不都合が生じたため、expand関数で解候補リストを作成する実装方針に変更しています。

02_tree_greedy.cpp

struct Greedy
{
    /// @brief greedyで行動を決定する
    /// @param state 初期状態
    /// @return 最も良い最終状態
    State solve(const State &state)
    {
        State now_state = state;
        while (true)
        {
            vector<State> next_states;
            now_state.expand(next_states);
            if (next_states.empty())
                break;
            ScoreType best_score = -1;
            for (auto &&next_state : next_states)
            {
                if (next_state.score > best_score)
                {
                    best_score = next_state.score;
                    now_state = next_state;
                }
            }
            // 全ての頂点を使い終わっていたら終了
            bool is_all_determined = true;
            for (int i = 0; i < N; i++)
                if (now_state.parents[i] == -2)
                {
                    is_all_determined = false;
                    break;
                }
            if (is_all_determined)
                break;
        }
        return now_state;
    }

};

根を評価する前と比べてスコアが伸びました。

手法 スコア 順位(当日相当)
順番にBFS 55988632 741位 提出リンク
BFSする根の順序を貪欲に選ぶ 58436941 689位 提出リンク

BFSする根の順序をビームサーチで選ぶ

基本的なビームサーチ

手法説明

さて、先ほどの貪欲法では、木を1本ずつ構築していく過程で、その時点でスコアが最大になる木を採用していました。
しかし、途中まで構築した解のスコアが最大でも、残った頂点で構築する木でスコアが伸ばせない場合、最終的な解のスコアが低い可能性があります。
そこで、途中時点で候補に挙がった部分解を複数個保持し、それぞれの部分解からさらに解を構築していくことを考えます。
以下の図では、木を1本構築するステップごとに解をスコア順に上位2個保持して進める例を示しています。
貪欲法の例と同じ入力から始めた結果、貪欲法のスコア135と比べ、スコア137で高くなっていることがわかります。
このように、解の候補を上位指定個数保持して解を構築する手法をビームサーチ、指定個数をビーム幅といいます。
多くの場合、ステップの考え方やスコア計算方法が同じであれば、貪欲法よりもビームサーチの方が最終結果が良くなります。

06_tree_beam.png

実装説明

貪欲法の実装でbest_scoreかどうかを判定してnow_stateを更新していたのに対し、ビームサーチでは、ビーム幅の個数分の解候補を保持して、その中で最もスコアが高いものを選択します。
現在のステップの解候補をnow_beam、次のステップの解候補をnext_beamに保持します。
now_beamに保持された全ての解候補からexpand関数を呼び出し、next_beamに解候補を追加します。
その後、next_beamの中から上位beam_width個を取り出し、now_beamと入れ替えます。
この操作を繰り返し、全ての頂点を使い終わったら終了します。
ここで使用するstd::partial_sort(first, middle, last)は、firstからlastまでの範囲の中から、上位k個を取り出し、先頭k個をソートした状態で返す関数です。(kはmiddle-first) 3

03_tree_beam_search.cpp

struct BeamSearch
{
    using ScoreType = int; // ゲームの評価スコアの型を決めておく。
    const int beam_width = 150;

    /// @brief 状態
    struct State
    {
        // ~~省略~~
        bool operator<(const State &other) const
        {
            return score < other.score;
        }
        bool operator>(const State &other) const
        {
            return score > other.score;
        }
        // ~~省略~~
    };

    /// @brief ビームサーチで行動を決定する
    /// @param state 初期状態
    /// @param beam_widths 深さごとのビーム幅
    /// @return 最も良い最終状態
    State solve(const State &state)
    {
        vector<State> now_beam;
        now_beam.emplace_back(state);
        vector<State> next_beam;
        while (true)
        {
            next_beam.clear();

            for (int i = 0; i < now_beam.size(); i++)
            {
                now_beam[i].expand(next_beam);
            }

            // 上位beam_width個を取り出す
            partial_sort(next_beam.begin(), next_beam.begin() + beam_width, next_beam.end(), greater<>());
            if (next_beam.size() > beam_width)
            {
                next_beam.resize(beam_width);
            }
            now_beam.swap(next_beam);
            auto best_state = now_beam[0];
            // 全ての頂点を使い終わっていたら終了
            // ~~省略~~
            if (is_all_determined)
                break;
        }
        auto best_state = now_beam[0];
        return best_state;
    }

    // ~~省略~~
};

多様性確保

手法説明

ビームサーチは多くの場合、今の実装ではいまいちです。
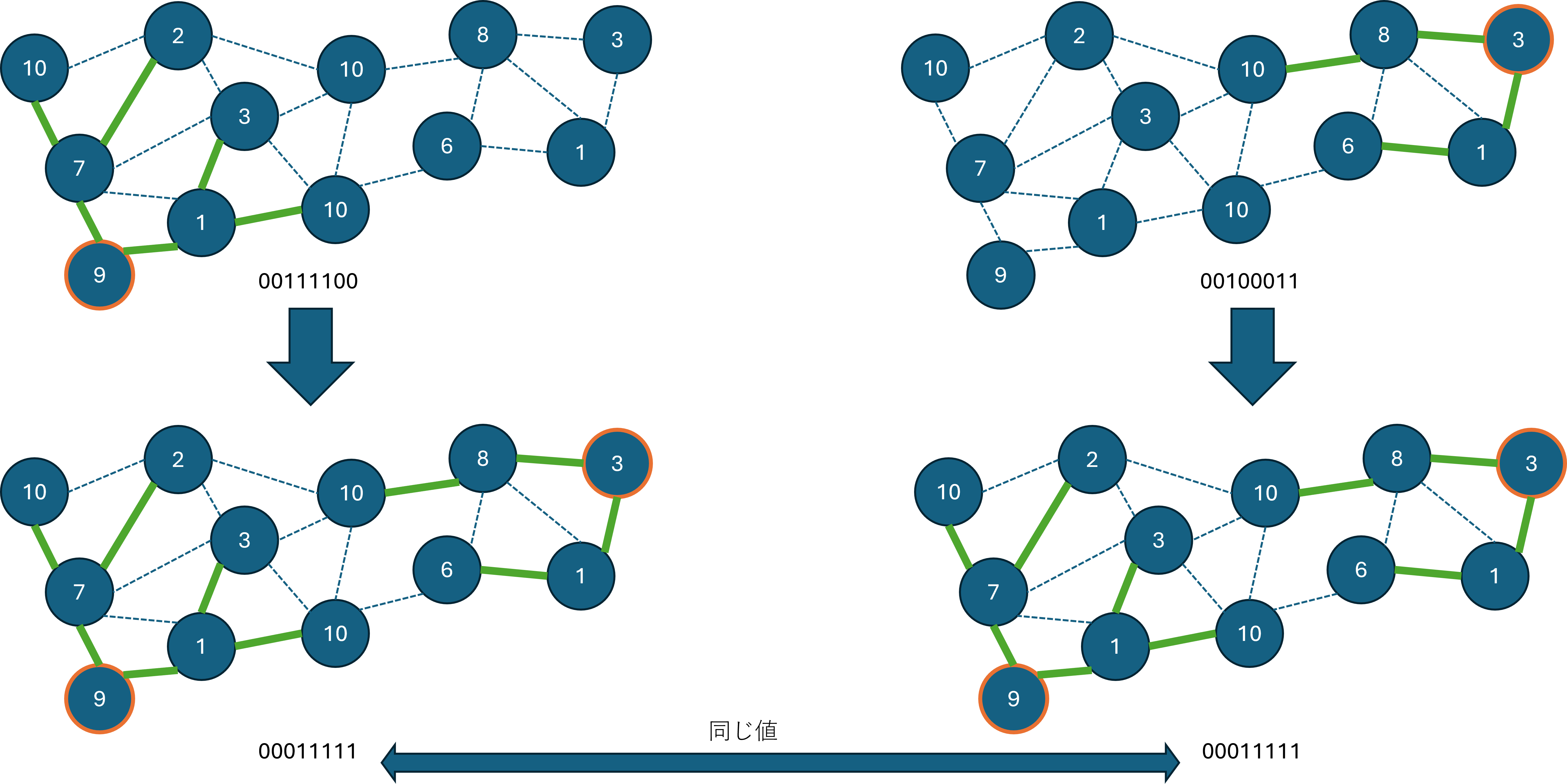
たとえば、以下のように、きれいさ9の頂点を根とした木ときれいさ3の頂点を根とした木を構築する場合、どちらを先にしても同じ状態になります。
ビーム幅を設定して探索しても、同じ状態ばかり残ってしまうと貪欲法との差があまりなくなってしまいます。
異なる状態が多く残ることを多様性があるといいます。
ビームサーチでは、多様性を確保するための工夫をなにかしら考えることが多いです。

07_tayousei.png

ここでは、zobrist hashを用いた同一盤面除去で多様性を確保します。
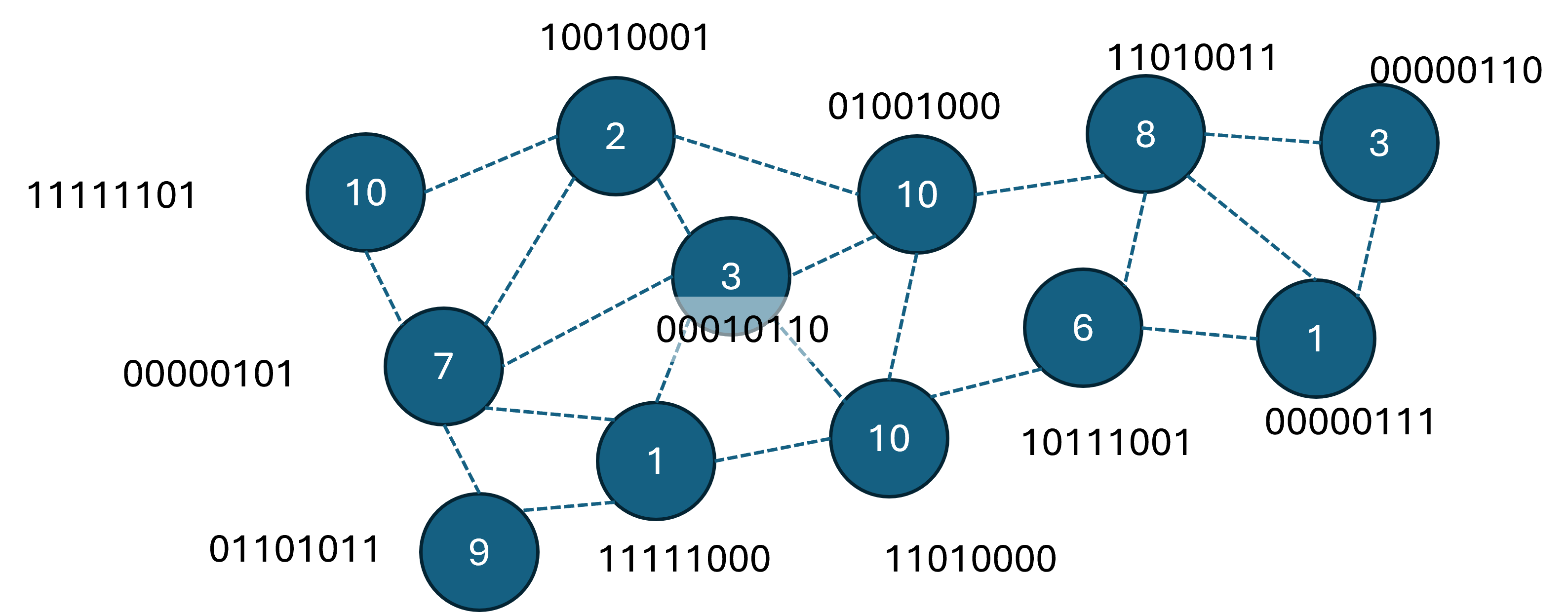
まず、状態を表す構成要素1つ1つに対応する乱数を用意します。
この問題では頂点や辺、高さなどが該当しますが、状態をざっくり表せる最低限の情報だけ使えばいいので、今回は各頂点を用います。

08_zobrist_init.png

状態のハッシュ値を計算するには、状態を表す構成要素の乱数全ての排他的論理和を計算します。
きれいさ9の頂点を根とした木のみを構築した状態については、

$11111101 \oplus 00000101 \oplus 01101011 \oplus 10010001 \oplus 00010110 \oplus 11111000 \oplus 11010000 = 00111100$

同様にきれいさ3の頂点を根とした木のみを構築した状態については$00100011$、
きれいさ3の頂点を根とした木ときれいさ9の頂点を根とした木を両方構築した状態については$00011111$となります。
このように、異なる状態のハッシュ値は異なる値、同じ状態のハッシュ値は同じ値となるため、状態が同じかどうかを判断するのに利用できます。
ハッシュが計算できたので、ビームサーチの過程で、探索済みのハッシュ値のセットに含まれている状態は追加しないようにすることで、同一盤面を探索せずに済みます。

09_zobrist_calc.png

実装説明

まず、各頂点を使用済みかどうかに対応する乱数を用意します。

03_tree_beam_search.cpp
struct PreProcessedData
{
    vector<uint64_t> using_hash;
    void preProcess()
    {
        setUsingHash();
    }

    void setUsingHash()
    {
        using_hash.resize(N);
        for (int i = 0; i < N; i++)
            using_hash[i] = rng.next();
    }
};
PreProcessedData pre_processed_data;

bfs関数で木の構築中に頂点を追加する際、その頂点の乱数とハッシュ値のxorをとり、ハッシュ値を更新します。
expand関数では、探索済みの状態を追加しないように条件分岐を入れます。
hashes.insert(ps.hash).secondは、hashes.insertでhashesに今回計算したハッシュ値を追加しつつ、ハッシュ値が既に存在していたらfalseを返すため、この条件分岐で探索済みの状態を追加しないようにしています。

03_tree_beam_search.cpp
struct BeamSearch
{
    using ScoreType = int; // ゲームの評価スコアの型を決めておく。
    const int depth = H;
    const int beam_width = 150;

    /// @brief 状態
    struct State
    {
        ScoreType score;
        uint64_t hash;
        vector<int> parents; // 各頂点の親の頂点。-1は根、-2は未確定
        // ~~省略~~

        void bfs(int root_i)
        {
            // ~~省略~~
                        q.push({d + 1, child});
                        hash ^= pre_processed_data.using_hash[child];
            // ~~省略~~
        }

        /// @brief 現在の状態から、次の状態リストを作る
        /// @param next_states 次の状態
        /// @param hashes 検討済みの状態のハッシュ値リスト
        void expand(
            vector<State> &next_states, unordered_set<uint64_t> &hashes) const
        {
            for (int i = 0; i < N; i++)
            {
                State ps = *this;
                ps.bfs(i);
                if (hashes.insert(ps.hash).second)
                {
                    next_states.push_back(ps);
                }
            }
        }
    };
};

貪欲法と比べてスコアが伸びました。
しかし、がんばったわりにはスコアも順位もたいして伸びていませんね。

手法 スコア 順位(当日相当)
BFSする根の順序を貪欲に選ぶ 58436941 689位 提出リンク
BFSする根の順序をビームサーチで選ぶ 59570116 664位 提出リンク

今回、木を構築する順序をビームサーチで決定しましたが、木1本の構築方法はBFSを使うことで決め打っていました。
木をBFSで構築する場合、親頂点の隣接点は未使用ならば必ず子頂点となり、親頂点の高さ+1の高さになります。
以下の例の場合、かなりきれいな頂点でも低い位置で木に含まれてしまい、もったいないです。
この例ならBFSの代わりにDFSで木を構築することで良い解が出せますが、どのみち「木1本を構築する」ことを1ステップとしてビームサーチをしている限り、計算時間を増やしても（極端な話、計算時間が無限でも）細かい解の調整ができないことに変わりありません。

10_bad_bfs.png

木を焼きなます

手法説明

前節の課題である、細かい解の調整方法を考えます。
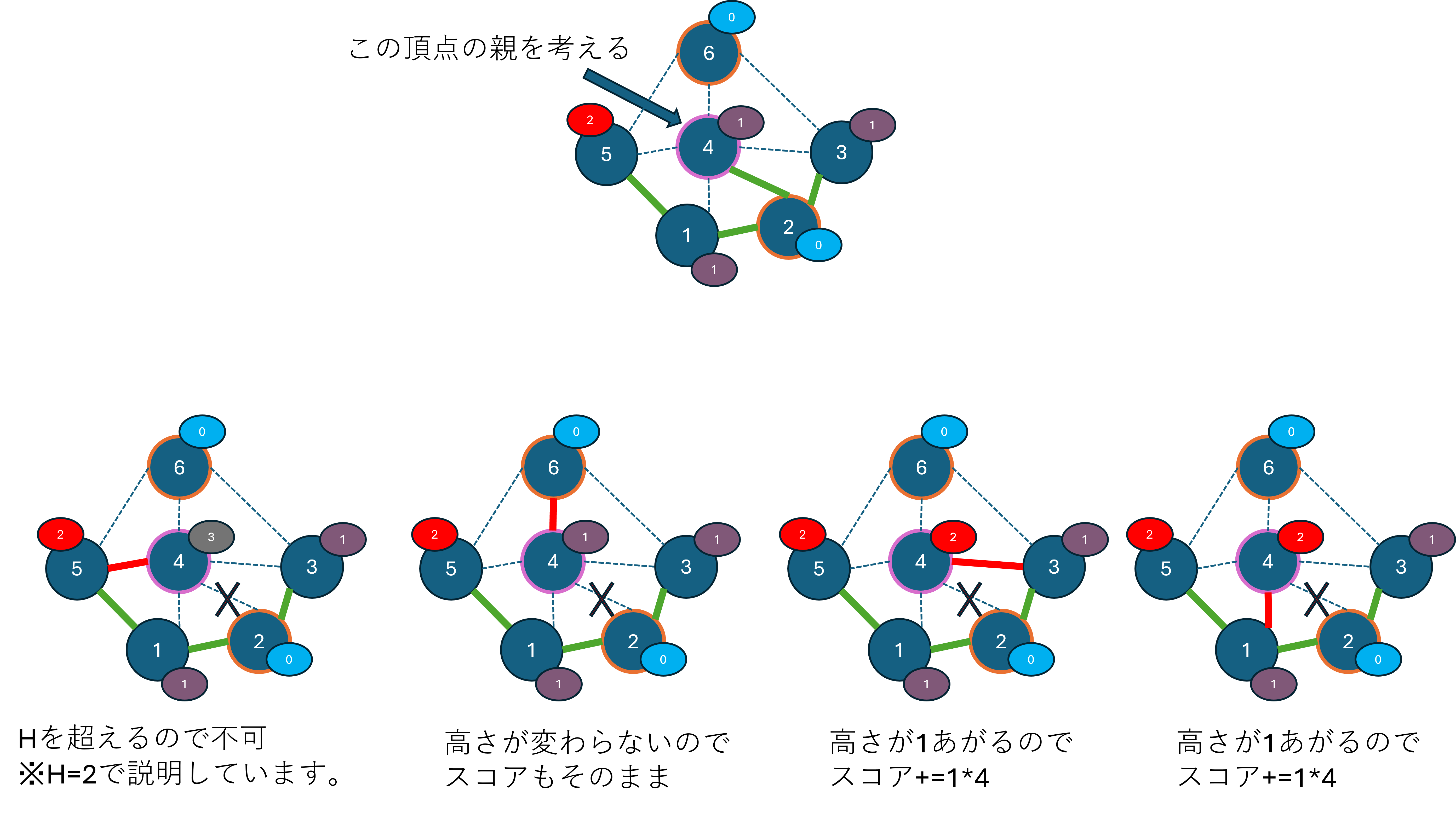
たとえば、以下のようにある頂点の親を別の親に変更することを考えます。
頂点4の親を頂点5に変更すると、高さがHを超えるため、このような変更はできません。
頂点4の親を頂点6に変更しても、高さが元のままなので、スコアは変わりません。
頂点4の親を頂点3に変更すると、高さ1上がるため、スコアが上がります。
頂点4の親を頂点1に変更すると、高さ1上がるため、スコアが上がります。
このように、「1つの頂点の親を可能な範囲で変更する」というのを繰り返して探索することで、よりよい解が見つけられそうです。
このように、解を少しずつ変更するのを繰り返しながら改善する手法は多く存在しますが、AHCでは多くの場合、山登り法や焼きなまし法が有効です。
これらの手法は AHC典型解法シリーズ第2弾「焼きなまし法」で説明していますので、焼きなまし法自体の詳細説明は割愛します。

11_bad_neigbour.png

ここで、頂点1の親を同じように変更することを考えます。
頂点1の変更先となる親頂点候補は頂点4だけなので、頂点4に変えてみます。
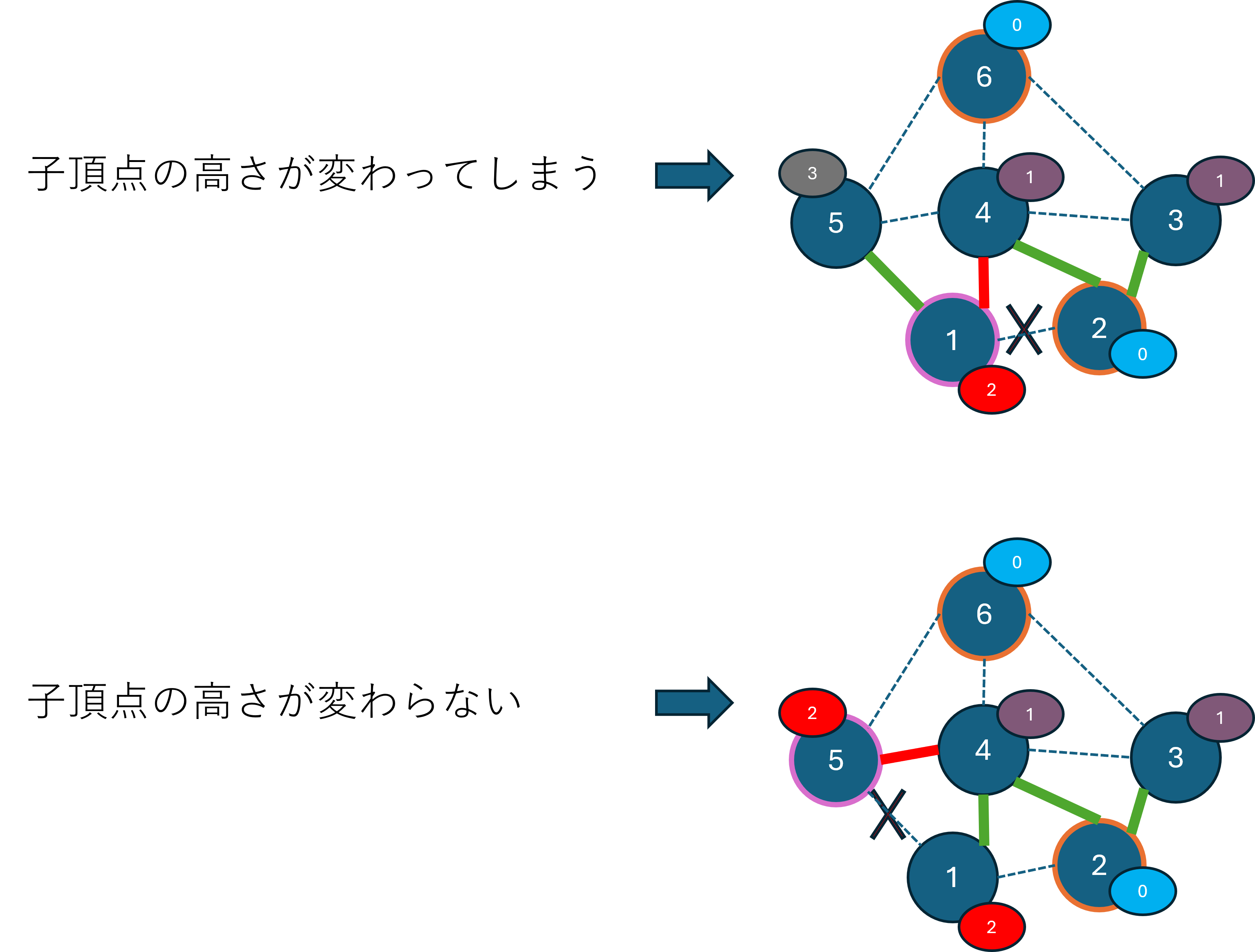
すると、先ほどと異なり、頂点1自身に子頂点があるため、頂点1の高さが1上がることで、子頂点である頂点5の高さも1上がり、Hを越えてしまいます。
このように、子を持つ頂点の親を付け替えたとき、子頂点の高さや、子頂点の子頂点の高さの更新と、スコア計算、制約チェックが必要になります。
これはかなり計算コストがかかるため、制限時間内で探索できる状態数が減ってしまいます。

12_child_check.png

ここで、ある頂点の親を変更するとき、子頂点側も別の頂点に親を付け替えることで、子頂点を高さを変えずに、自分自身の高さだけを変えることができます。
これなら高さの更新やスコア計算、制約チェックが自分自身のみで完結するので、計算コストが低くなりますね。

13_swap_parent.png

さて、今紹介した方針を実装する前に、気づけそうなことがあります。
先ほどの説明からわかるように、スコアに関係するのは「親が具体的にどの頂点であるか」ではなく、「親頂点の高さ」です。
たとえば、以下の図のように、各頂点の高さだけ決めてから、その高さを再現できるように親頂点を決めてみます。
どれも異なる解のように見えますが、スコアが同じであることがわかります。
今回の問題でプログラムが出力する必要があるのは「各頂点の親頂点」なので、自然に問題を読むと「各頂点の親頂点を決める問題」と解釈できます。
しかし、制約を満たす範囲で各頂点の高ささえ決めておけば、どんな親のつけ方をしても同じスコアになることから、「各頂点の高さを決める問題」と置き換えることができます。
このように問題を置き換えることで、コスト面で都合がよくなります。

  • 子頂点の親をつけかえる処理が不要になる（ただし、子頂点のつけかえ先になる親頂点があるかどうかの判定は必要）
  • 高さの影響が同じ近傍を1つにまとめられるため、探索空間が減る

このような問題設定の解釈を置き換えはAHCではブレークスルーになることもあるため、ぜひ覚えておくとよいでしょう。

14_height_neigbour.png

実装説明

まず、各頂点の隣接点を高さごとに何個あるか数えます。
全ての頂点の高さを0にした状態から始めるなら、全てのiについて、next_height_cnt[i][0]は隣接点の数と同じです。

04_simulated_anealing.cpp
struct SimulatedAnnealing
{
    //~~省略~~
    // 頂点iの隣接点を高さごとに何個あるか数える。
    // e.g. next_height_cnt[i][h]=2なら、頂点iの隣接点のうち、高さhの頂点が2個ある。
    int next_height_cnt[N][H + 1];
    vector<int> heights;
    int score = 0;

    vector<int> best_heights;
    int best_score = 0;

    SimulatedAnnealing(const vector<int> &heights) : heights(heights)
    {
        // 各頂点の隣接点を高さごとに何個あるか数える。
        for (int i = 0; i < N; i++)
            for (int j = 0; j < H + 1; j++)
                next_height_cnt[i][j] = 0;
        for (int i = 0; i < N; i++)
        {
            score += A[i] * (heights[i] + 1);
            for (auto &e : G[i])
            {
                assert(e < heights.size());
                assert(heights[e] < H + 1);
                next_height_cnt[i][heights[e]]++;
            }
        }
    }
};

ランダムに選んだ頂点curの高さを変更します。
頂点curの新しい高さは、ランダムな隣接点の高さ+1にできそうです。
しかし、curに子頂点eがある場合、eの高さを変えないようにするには、cur以外にcurと同じ高さの頂点がeと隣接している必要があります。
ここで、先ほど用意したnext_height_cntを使うと、curと同じ高さの頂点がeの隣接点に何個あるかわかります。
ここにはcur自身も含まれているので、next_height_cntが1でなければ、eの高さを変えずにすみます。
curの全ての子頂点について、高さを変えずに済むならcurの高さを変えられます。
curの高さを変えた場合は、curの隣接点全てのnext_height_cntを更新前の高さは1減らし、更新後の高さは1増やせばよいです。

04_simulated_anealing.cpp
struct SimulatedAnnealing
{
    //~~省略~~

    void solve(double time_limit)
    {
        //~~省略~~


        // 1点の深さを変更
        int cur = rng.randrange(N);
        int new_parent = G[cur][rng.randrange(G[cur].size())];
        int prev_height = heights[cur];
        int new_height = heights[new_parent] + 1;
        if (rng.randrange(10) == 0)
            new_height = 0;

        if (new_height > H)
            continue;
        if (new_height == heights[cur])
            continue;

        //~~省略~~

        // 変更しても木が構築可能かチェック
        // 対象頂点に子の頂点がある場合、その子が別の頂点を親にできれば、
        // 子の高さを変えずに済む。
        // よって、対象頂点の子とつながる頂点が他に対象頂点の元の高さと同じ高さの頂点を持つかどうかをチェックする。
        bool can_change = true;
        for (auto &e : G[cur])
            if (heights[e] == prev_height + 1)
            {
                if (next_height_cnt[e][prev_height] == 1)
                {
                    can_change = false;
                    break;
                }
            }
        if (!can_change)
            continue;

        // 更新
        score += score_diff;
        heights[cur] = new_height;
        for (auto &e : G[cur])
        {
            next_height_cnt[e][prev_height]--;
            next_height_cnt[e][new_height]++;
        }

        if (best_score < score)
        {
            best_score = score;
            best_heights = heights;
        }
         //~~省略~~

};

解を「各頂点の高さ」で保持しているので、問題文の要求通り、「各頂点の親頂点」に変換して出力する関数を用意します。
先述の通り、親の高さ+1が子の高さになってさえいれば、どの頂点を親として扱ってもよいです。
以下のコードでは、高さの条件を満たす隣接点をみつけるたびに、その隣接点を親として更新しています。

04_simulated_anealing.cpp
/// @brief 各頂点の高さを元に親を復元して出力
/// @param heigts 頂点iの高さ
void output(vector<int> &heigts)
{
    vector<int> p(N, -1); // 頂点iの親の頂点
    for (int i = 0; i < N; i++)
    {
        if (heigts[i] == 0)
        {
            p[i] = -1;
        }
        else
        {
            for (auto to : G[i])
            {
                if (heigts[to] + 1 == heigts[i])
                {
                    p[i] = to;
                }
            }
        }
    }
    for (int i = 0; i < N; i++)
        cout << p[i] << " \n"[i + 1 == N];
}

先ほどの木を1本構築するのを1ステップとしたビームサーチと比べて、大幅にスコアが伸びました。パフォーマンスは2色上がっているので、木自体を細かく調整することがいかに今回の問題で大事かがわかりました。

手法 スコア 順位(当日相当)
BFSする根の順序をビームサーチで選ぶ 59570116 664位 提出リンク
木を焼きなます 70420513 291位 提出リンク

深さを低い順に選ぶ

手法説明

さて、名前のついた手法でいえば、現時点で「ビームサーチのスコアよりも焼きなまし法のスコアが高い」です。
ここで「ビームサーチのスコアよりも焼きなまし法のスコアが高いから、この問題においてビームサーチは悪手であり、焼きなまし法を使う問題だ」と考えるのは早計です。
というのも、ビームサーチを使うにしても、焼きなまし法を使うにしても、探索の1ステップで解をどのように変更するかは、今説明した以外にも複数考えられるからです。

問題に合わせて探索の仕方を工夫してみましょう。
今回の問題の特徴を振り返ります。

  • ある頂点の高さをHにするためには、高さH-1の隣接点が必要
  • 1頂点のスコアだけならば、高さHの頂点が最大スコア

全頂点を高さHにすることはできないので、どんなにがんばってもスコアは$H \times N$未満になります。
スコアを$H \times N$に近づけるためには、低い頂点をなるべく減らす必要があります。

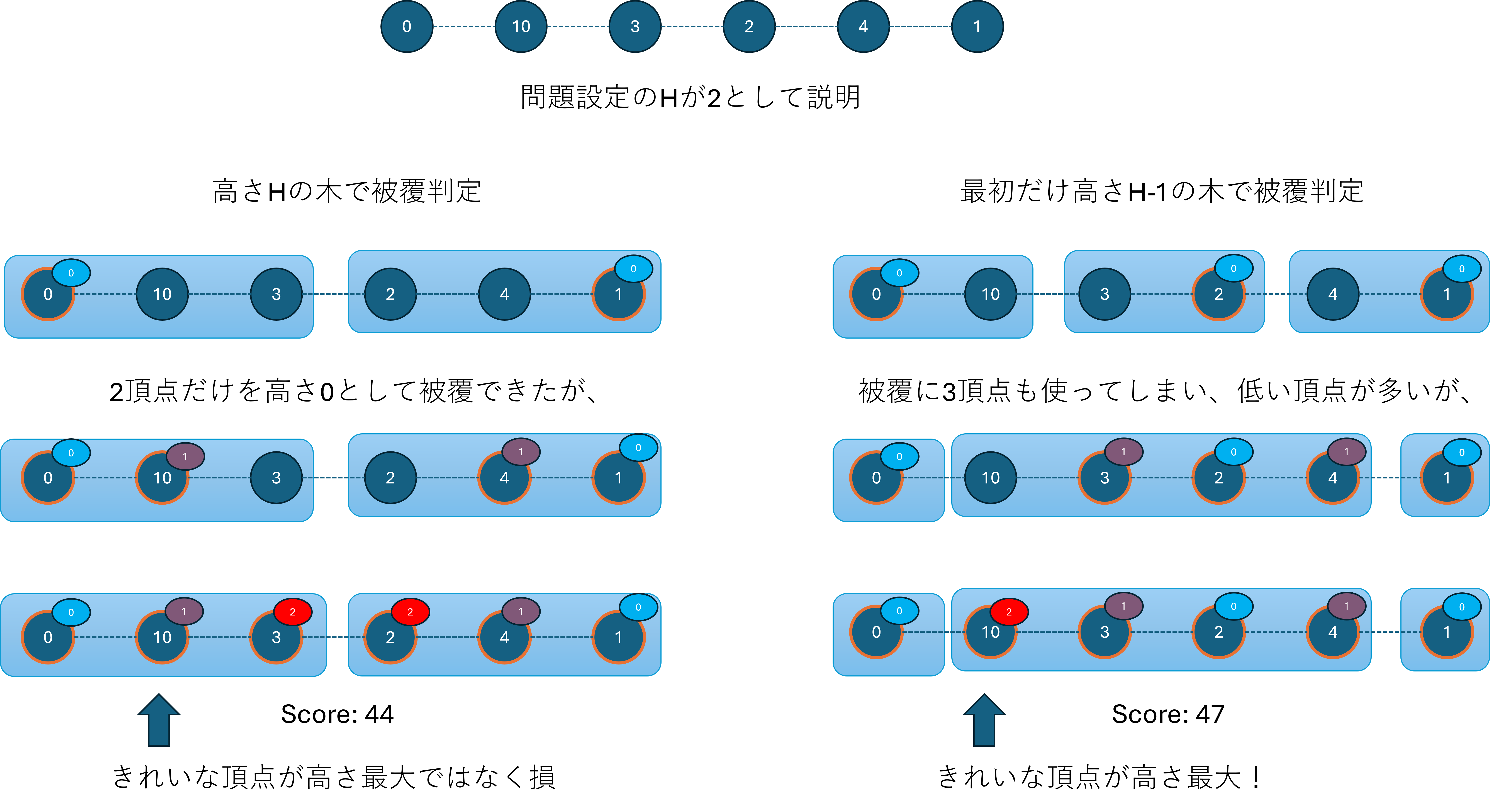
そこで、低い高さから順に、「高さhにする頂点」を選んでいくことを考えます。
「高さhにする頂点」を選ぶとき、既に選んだ高さh-1以下の頂点と、今選ぶ頂点から伸ばせる木の集合で全頂点を埋めることができれば、残った頂点は必ず高さh+1以上の頂点だけにできます。
このような条件を満たす頂点を、なるべくきれいではなく、なるべく少なく選ぶことができれば、最終ステップ付近ではきれいな頂点をたくさん高い頂点候補として残すことができます。

具体的には、以下の方法でこれが実現できます。


高さ0からHまで、以下の手順を繰り返す
    高さhにできる頂点iをきれいさで昇順に並べ、以下の手順を繰り返す
        頂点iから高さHまでBFSで木をつくり、仮置きする。
        もし、既に確定した頂点と、今回仮置きした木の集合で全頂点を覆えるなら、繰り返しを抜ける
    仮置きした木はなかったことにするが、仮置きに使った高さhの頂点は確定する

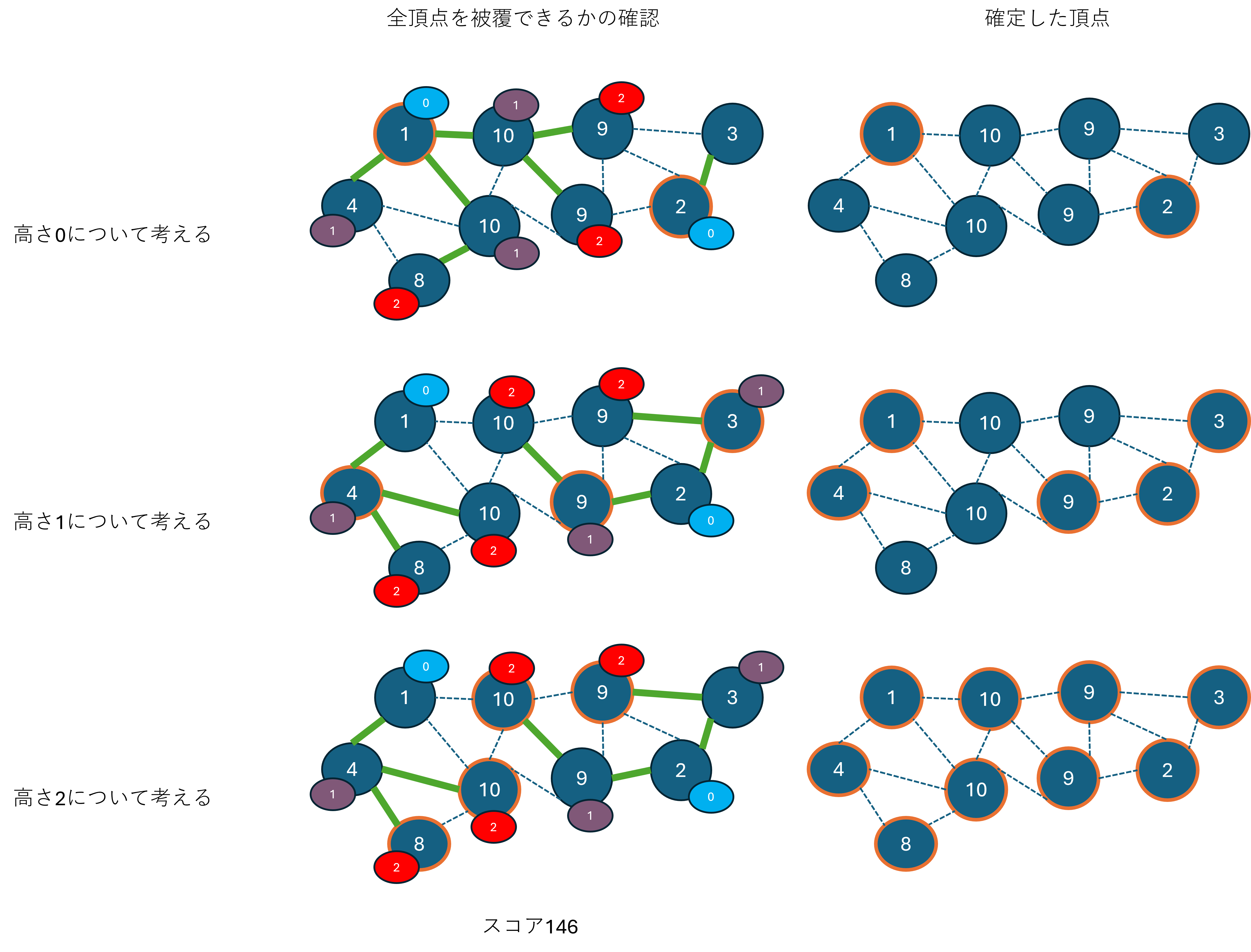
この流れを以下に図示しました。
入力例は先ほどの木の構築を1ステップとするビームサーチと同じものを使用していますが、先ほどのスコア137よりも高い、スコア146が達成できました。
高さHの頂点が先ほどは3個だったのに対し、今回は4個となっています。きれいな頂点が高さHのために残っていることも含め、狙い通りの動きになっていることがわかります。

15_height_rule.png

実装説明

まず、頂点をきれいさで昇順に並べて準備しておきます。

05_depth_greedy.cpp
struct PreProcessedData
{
    vector<int> ord; // きれいさで昇順に頂点のインデックスを並べたもの
    void preProcess()
    {
        setOrd();
    }

    void setOrd()
    {
        ord.resize(N);
        for (int i = 0; i < N; i++)
            ord[i] = i;
        sort(ord.begin(), ord.end(), [&](int x, int y)
             { return A[x] < A[y]; });
    }
};

使用済みの頂点を管理するために、boolの配列に名前をつけ、論理和をとる関数と、全ての要素がtrueかどうかを判定する関数を用意します。4

05_depth_greedy.cpp
using Bools = array<bool, N>;
// 配列の要素ひとつひとつの論理和をとる
Bools allOr(const Bools &a, const Bools &b)
{
    Bools ret = {};
    for (int i = 0; i < N; i++)
        ret[i] = a[i] || b[i];
    return ret;
}

// 配列の全ての要素がtrueかどうかを判定する
bool isAllTrue(const Bools &bs)
{
    for (int i = 0; i < N; i++)
        if (!bs[i])
            return false;
    return true;
}

現在の状態から、次の状態を作る関数を用意します。
tree_candidatesは、今の高さに加えられる頂点からつくった木の候補リストです。
tree_candidatesで使用済み頂点を更新していき、さきほど作ったisAllTrueによって、全頂点を被覆できるかどうかを判定します。

05_depth_greedy.cpp
    /// @brief 状態
    struct State
    {
        ScoreType score;
        Bools all_has_i;  
        vector<Bools> height_has_i; // height_has_i[l][i]==1なら高さlに頂点iがある

        /// @brief 現在の状態から、次の状態
        State getNextState() const
        {
            // ~~~省略~~~
            vector<Bools> acc(candidates_size + 1, all_has_i);
            // ~~~省略~~~
            // tree_candidatesはきれいさが昇順なので
            // そのまま順番に見ることできれいじゃない頂点から順に判定できる
            for (int i = 0; i < candidates_size; i++)
            {
                acc[i + 1] = allOr(acc[i], tree_candidates[i].second);
                if (isAllTrue(acc[i + 1]))
                {
                    last = i;
                    break;
                }
            }
            // ~~~省略~~~
        }
    };

ここで一工夫してみます。
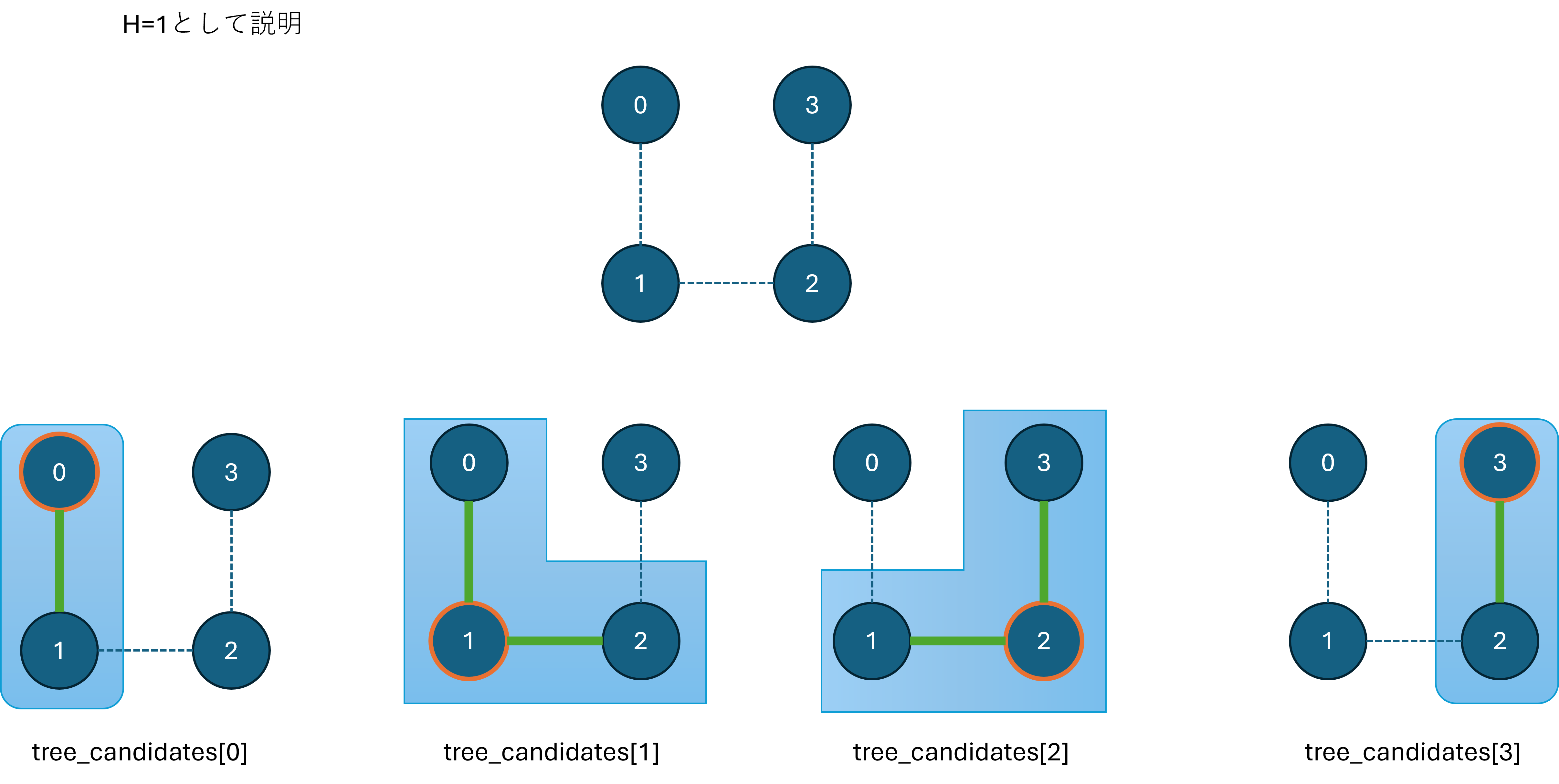
簡単のため、H=1として説明します。
以下のような4頂点の入力の場合、各頂点からできる木の候補は以下のようになります。

16_candidates.png

これらの木候補を根のきれさで昇順に合わせていくと、頂点0,1,2の3頂点の木で全頂点を被覆できます。
よって、深さ0として決定するのはこの3頂点でよいでしょうか？

17_muda_points.png

ここで、頂点0から順に頂点i-1までの木の共通頂点を加えたものtree_candidates[0~i-1]と、その逆順に頂点i+1までの木の共通頂点を加えたものtree_candidates[last~i+1]を用意します。
もし、tree_candidates[0~i-1]とtree_candidates[last~i+1]の共通頂点だけで全頂点を被覆できるなら、tree_candidates[i]は加える必要がありません。

18_slide_set.png

今の説明のtree_candidates[0~i-1]にあたる情報をacc[i]として先に用意し、tree_candidates[last~i+1]にあたる情報は逆順にたどる過程でcurとして更新しながら、iを含めるかどうかをチェックすることで実装できます。
なお、高さ1以上の時は、確定済み頂点をall_has_iとしてcurの初期値にします。

05_depth_greedy.cpp
    /// @brief 状態
    struct State
    {
        ScoreType score;
        Bools all_has_i;  
        vector<Bools> height_has_i; // height_has_i[l][i]==1なら高さlに頂点iがある

        /// @brief 現在の状態から、次の状態
        State getNextState() const
        {
            // ~~~省略~~~
            vector<Bools> acc(candidates_size + 1, all_has_i);
            // ~~~省略~~~
            // tree_candidatesはきれいさが昇順なので
            // そのまま順番に見ることできれいじゃない頂点から順に判定できる
            for (int i = 0; i < candidates_size; i++)
            {
                acc[i + 1] = allOr(acc[i], tree_candidates[i].second);
                if (isAllTrue(acc[i + 1]))
                {
                    last = i;
                    break;
                }
            }
            Bools cur = all_has_i;
            for (int i = last; i >= 0; i--)
            {

                // acc[i]はtree_candidates[0~i-1]までの全ての木の頂点が含まれており、
                // curはtree_candidates[i+1~last]までの全ての木の頂点が含まれている
                // よって、acc[i] or curが全体を被覆できるなら、tree_candidates[i]は加えない
                if (isAllTrue(allOr(acc[i], cur)))
                {
                    continue;
                }
                cur = allOr(cur, tree_candidates[i].second);
                use[tree_candidates[i].first] = true;
                nscore -= (10 - height) * A[tree_candidates[i].first];
            }
            // ~~~省略~~~
        }
    };

この実装により、パフォーマンスは2色上がり、ついに1ページ目に載る順位です。
冒頭に書いたように、AHCが「焼きなまし法やビームサーチを知らないと戦えない」ものではないことがわかりますね。

手法 スコア 順位(当日相当)
木を焼きなます 70420513 291位 提出リンク
深さを貪欲に選ぶ 76105643 19位 提出リンク

深さをビームサーチで選ぶ

手法説明

今説明した手法では、深さごとのステップで、残った頂点できれいさの昇順に候補をつくっていました。
これだと1通りしか候補をつくらないため、ビームサーチに拡張できません。（先述のtree_candidatesを見ると複数候補っぽいですが、これは1ステップあたりの1候補を構成する要素であり、1ステップ、つまり深さを1進めた状態の候補は1通りしかありません。）
ここで、各頂点のきれいさに乱数を加えることで、「だいたいきれいさの昇順だが、ある程度逆転も起きるランダムな順番」で被覆判定ができます。
これにより、各深さで異なる頂点集合を候補とすることができるため、ビームサーチに拡張できます。

実装説明

各頂点のきれいさに乱数を加えてソートする実装です。
乱数の範囲を0~49にすることで、きれいさが50以上離れた頂点同士の順序は絶対逆転せず、かつきれいさが近いほど順序が逆転しやすいようになります。
これで「だいたいきれいさの昇順だが、ある程度逆転も起きるランダムな順番」を実現できます。

06_beam_search.cpp
for (auto &&[tree_root, tree_bs] : tree_candidates)
{
    random_value[tree_root] = A[tree_root] + rng.randrange(0, 50);
}
sort(tree_candidates.begin(), tree_candidates.end(), [&](auto &x, auto &y)
        { return random_value[x.first] < random_value[y.first]; });

ビームサーチ自体のおおまかな実装方法は先ほど説明したので省略します。

手法 スコア 順位(当日相当)
深さを貪欲に選ぶ 76105643 19位 提出リンク
深さをビームサーチで選ぶ 77172744 1位 提出リンク

いろいろ工夫

手法説明

おおまかな方針がうまくいったので、いろいろ工夫してみます。

  • ビーム幅を深さごとに変更
    今回の問題では、ステップが進むにつれて使用済み頂点が増え、候補数が減っていきます。
    わかりやすい例では、深さH-1までの頂点で、深さHの頂点の決め方が1通りに絞れるので、深さＨの頂点を決めるためにビーム幅を2以上にするのは全く意味がありません。
    一方で、深さ0の頂点を決める時点では候補が多いため、ビーム幅を大きくしてもよいでしょう。
    これらの考察から、ビーム幅を深さごとに変更することで、より良い解を出せる可能性があります。

  • 最適化オプションを変更
    制限時間内でビームサーチをするなら、処理が高速であるほどビーム幅を増やせるため、より良い解がみつけやすくなります。
    そのため、最適化オプションをより強いものにすることで高速化を図ります。

  • 被覆判定に使う木の高さを調整
    ここまでの手法では、被覆判定を問題通り高さHの木で行っていました。
    「高さの低い頂点を減らす」という目的ではこれでよいですが、「きれいな頂点を高い頂点にする」ことを考えたとき、被覆の都合できれいな頂点を低くせざるを得ない場合があります。そこで、低い頂点を決定する時点の被覆判定に使う高さを低くすることで、わざと低い頂点を増やすことで、その後の頂点選択を柔軟にすることを考えます。

    19_adjust_height.png

実装説明

ビーム幅を高さに合わせて変更する実装です。
今回はプログラムで線形に減らす実装をしましたが、手打ちで好きな値を配列で消えてもいいです。

07_efficient.cpp
//@brief startからendまでの範囲でprogressに応じて一定量で減少した値をとる
//@param start 開始値
//@param end 終了値
//@param progress 進捗度(0~1)
//@return 進捗に合わせた値
double linear_decrease(double start, double end, double progress)
{
    return start - (start - end) * progress;
}

vector<int> get_beam_widths(const int start_width, const int end_width, const int size)
{
    vector<int> beam_widths(size);
    for (int i = 0; i < size; i++)
    {
        beam_widths[i] = linear_decrease(start_width, end_width, i / (size - 1.0));
    }
    return beam_widths;
}

State solve(const State &state)
{
    // ~~~省略~~~
    for (int t = 0; t < beam_depth; t++)
    {
        int beam_width = beam_widths[t];
        // ~~~省略~~~

        // 上位beam_width個を取り出す
        partial_sort(next_beam.begin(), next_beam.begin() + beam_width, next_beam.end(), greater<>());
        if (next_beam.size() > beam_width)
        {
            next_beam.resize(beam_width);
        }
    // ~~~省略~~~
    }
    // ~~~省略~~~
}

最適化オプションは、例えばg++でコンパイルする場合、g++ -O3 -funroll-loops hoge.cppのような最適化オプションをしたいとき、ファイル内に#pragma GCC optimizeで直接指定できます。
AtCoderではコンパイルコマンドを自分で指定できないので、オプションを指定するならこのような方法が必要です。

  • O3: AtCoderのデフォルト指定のO2よりも最適化を強くする
  • unroll-loops: ループを展開する
07_efficient.cpp
#pragma GCC optimize("O3")
#pragma GCC optimize("unroll-loops")

unroll-loopsがわかりにくいかと思いますが、ループ処理をコンパイル時に展開することで、ループのオーバーヘッドを軽減させることができます。プログラムによって効果はまちまちです。

07_efficient.cpp
// 通常コード
// iのインクリメント++iとか条件チェックi<4とかでオーバーヘッドが生じる
for (int i = 0; i < 4; ++i) { 
    array[i] = array[i] * 2;
}

// 展開後
array[0] = array[0] * 2;
array[1] = array[1] * 2;
array[2] = array[2] * 2;
array[3] = array[3] * 2;

被覆判定に使う木の高さを調整する実装です。
getTreeCandidatesの中で行うbfsには、残る木の高さhを引数にしているので、hを現在の高さheightに応じて変化させます。

07_efficient.cpp
vector<pair<int, BitSet>> getTreeCandidates(BitSet &all_has_i, vector<int> &addible_roots) const
{
    // ~~~省略~~~
    for (int i = 0; i < candidates_size; i++)
    {
        // 残りの木の深さを計算
        int h = H + 1 - height;
        // 序盤は浅めに木を作ることで、選択肢を広げる
        if (height <= 2)
        {
            h -= 3 - height;
        }
        auto tree_bitset = bfs(addible_roots[i], h, all_has_i);
        // ~~~省略~~~
    }
    return tree_candidates;
}

少しスコアが伸びました。

手法 スコア 順位(当日相当)
深さをビームサーチで選ぶ 77172744 1位 提出リンク
深さをビームサーチで選ぶ（いろいろ工夫） 77353254 1位 提出リンク

深さをビームサーチで選んだ後に焼きなます

手法説明

さて、本記事はビームサーチがメインテーマなのでこれで終わりでもいいんですが、最後に「ビームサーチだけより、焼きなましだけより、両方を組み合わせたほうがいい場合がある」ことを学びましょう。
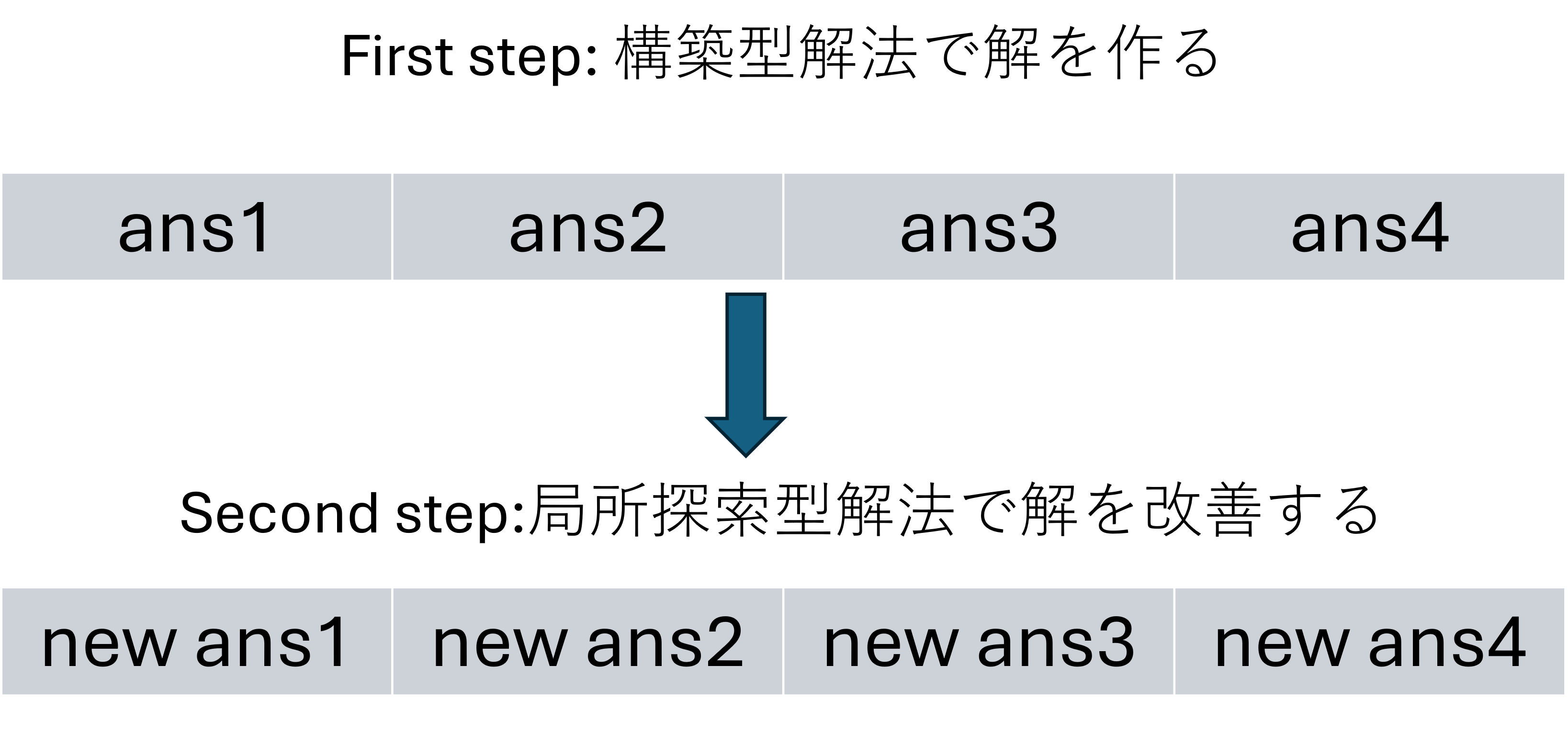
AHCでよく使う探索アルゴリズムは、貪欲法やビームサーチのように解を部分的に構築していくもの（ここでは構築型解法と呼びます）と、山登り法や焼きなまし法のように解の一部を徐々に変化させていくものが（ここでは局所探索型解法と呼びます）あります。
構築型解法は解がなにもない状態から解をつくるのに対し、局所探索型解法はなにかしらの初期解をもとに解を改善する違いがあります。
先ほどの焼きなましの例ではなにも解がない状態から始めたように見えるかもしれませんが、「全ての頂点が根」という初期解からスタートしていました。

20_answer_type.png

局所探索型解法は初期解をもとに改善するので、初期解が良い解だとより速く良い解にたどりつきやすくなります。
そこで、構築型解法で解を作り、その後局所探索型解法で改善するという方針もよさそうです。

21_fusion.png

深さをビームサーチで選ぶ（いろいろ工夫）の提出結果を見ると、実行時間の最大値は1933msで、これ以上ビーム幅を増やすというのは難しそうです。
一方で、短い実行時間のものは1799msでまだ時間に余裕があり、まだ改善の余地がありそうです。
計算時間を動的に制御する方法として、ビームサーチからchokudaiサーチに変更するか、ビームサーチでできた解を局所探索型解法で改善するか、の2つが考えられます。
chokudaiサーチにしても、オーバーヘッド分で探索量が増える恐れや、同じ探索方法をとっている以上、あまりスコア改善に寄与しないかもしれません。
そこで、ビームサーチでの1ステップと異なる遷移ができる焼きなまし法で改善するほうが、改善幅が大きそうです。
今回は、先ほどつくった焼きなまし法のコードをそのまま流用して、ビームサーチでできた解を改善する方法を試してみます。

実装説明

ビームサーチにかかった時間を計測し、制限時間の2sよりやや少ない1.98sのうち、残った時間で焼きなましを行います。
合計時間を2sにしないのは、出力や後処理のオーバーヘッドで制限時間をオーバーするのを防ぐためです。

08_complete.cpp
int main()
{
    input();
    pre_processed_data.preProcess();
    BeamSearch beam_search;
    vector<int> heights = beam_search.getAnswer();
    double elapsed_time = timer.getTime();
    cerr << "elapsed_time for beam search: " << elapsed_time << endl;
    double remaining_time_limit = 1.98 - elapsed_time;
    if (remaining_time_limit > 0)
    {
        timer.reset();

        SimulatedAnnealing annealing(heights);
        annealing.solve(remaining_time_limit);
        cerr << annealing.best_score << endl;
        heights = annealing.getAnswer();
        elapsed_time += timer.getTime();
        cerr << "elapsed_time for annealing: " << elapsed_time << endl;
    }

    output(heights);
}

スコアがさらに伸び、ついに（提出時点で）延長戦1位になりました。

手法 スコア 順位(当日相当)
深さをビームサーチで選ぶ（いろいろ工夫） 77353254 1位 提出リンク
深さをビームサーチで選んだ後に焼きなます 77414595 1位（既に抜かれたが、提出時点では延長戦でも1位）提出リンク

最後に

この記事では、ビームサーチを用いた解法を紹介しました。
今回で、AHC典型シリーズで紹介しようと思っていた解法は以上となります。
AHCでよく使われる大きな手法はだいたい網羅できたと思っています。

一方で、このシリーズで紹介していない有効なテクニックはまだたくさんあると思います。

例

  • 推定系の問題におけるMCMC
  • ビームサーチを状態コピーではなく差分更新で実装する

これらの手法について、シリーズの続編を書くかどうかは迷っていますが、ひとまずこの第4弾まで読み切れば、AHCで「この手法さえ知っていればもっと改善できたのに」という嘆きをすることは大幅に減ると思います。
本記事シリーズを読んで、少しでも多くの皆さんがAHCを楽しんでいただければ幸いです。

最後に、今回の実装にあたり、上位のいろいろな人のコードを参考にしつつ、MathGorillaさんにものすごく大きなアドバイスをいただいたので謝辞を述べさせていただきます。

サンプルコード一覧

  1. https://x.com/terry_u16/status/1881006063962694136 ↩

  2. 問題に与えられる情報に不確定要素がなく、全ての情報が最初に開示されている場合はビームサーチが貪欲法より悪くなることはないです。与えられる情報が不完全な場合はビームサーチの方が貪欲法より悪くなる場合もあります。 ↩

  3. std::sortで実装してもいいですが、std::sortは平均計算量が$O((last-first)log(last-first))$であるのに対し、std::partial_sortは$O((last-first)log(middle-first))$であるため、計算量が少なくて済みます。「ゲームで学ぶ探索アルゴリズム実践入門」ではpriority_queueを用いていますが、これはchokudaiサーチを説明する上でビームサーチからステップアップするのにわかりやすいからです。 ↩

  4. これより後のコードでしれっと使っていますが、std::bitsetのほうがいいです。bit演算になじみがない人向けの説明として用意しました。usingになじみがない可能性とか、そもそもstd::bitsetを知ってる人にとっては自作関数の方がわかりにくいかも、とかいろいろ悩んだので、苦肉の策です。 ↩

13
9
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
13
9

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?