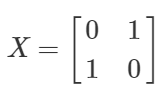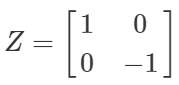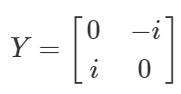More than 1 year has passed since last update.

量子コンピューティング by NRIAdvent Calendar 2021

@shnchr(Shinichiro Ohno)in

株式会社野村総合研究所

パウリゲート（XZY）を細かく見てみる

Last updated at 2023-07-18Posted at 2021-01-05

この記事について

量子ゲート型で主に意識するパウリゲートについて整理していきます。

最初に出てくる量子状態の表現方法（線形重合せ、bra-ket）と基本操作であるパウリゲート（XZY）についてまとめてみました。
ブロッホ球については、パウリゲート習熟後のほうがわかりやすいと思ったので、次回以降で触れていこうと思います。

理解が異なる点や補足事項等あればコメント頂ければ幸いです。

また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。

\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}

量子状態の表現

量子ビットと古典ビットの最大の差は、状態の持ち方にあります。
古典ビットでは、回路素子に関して基準電圧に対する電圧値の上下（$V_{high},V_{low}$）により計算過程においても、確定的な状態を持ちます。
一方、量子ビットにおいては、計算過程において、0と1のビットの重ね合わせ状態を用いる為、ビットが重なり合う状態を表現できるような数理モデルが必要となります。
この重ね合わせがどのように数式で表現されるのか？という点から始めたいと思います。

量子状態は、重ね合わせ状態を表現するために下記のように表現します。
雰囲気的には、$\alpha$程度で0になりそう、$\beta$程度で1になりそうという状態を重ね合わせで保持します。¹

|\psi〉 = \alpha\ket{0} + \beta\ket{1}\ \ \ \ \alpha ,\beta \in \mathbb{C_{複素数}}

α,βは複素数で実部、虚部があるため自由度は4となります。

\displaylines{
\alpha = a_{①実部} + a_{②虚部}i \\
\beta  = b_{③実部} + b_{④虚部}i
}

ただし、規格化条件により下記を満たす必要があり、この束縛で自由度は3となります。²

|\alpha|^2 + |\beta|^2 = 1

bra-ket記法

bra-ket

上記で登場した$\ket{0}$とか$\ket{1}$について説明しておきたいと思います。
これは、bra-ket記法というもので、後々に便利なので今導入しておきます。
ポール・ディラックが発明したのでディラックの記法とも呼ばれます。
braとketはそれぞれ、行（横）ベクトルと列（縦）ベクトルを表すものです。

\displaylines{
bra :\ \  \bra{a} =\yoko{a_{0}}{a_{1}} \\
ket :\ \  \ket{b} =\tate{b_{0}}{b_{1}}
}

braとketの積

行ベクトルと列ベクトルなので、その積は行列もしくは内積となります
また内積は「|」が2本となるので、1本に省略することができます

内積（横×縦）　：　\bra{a}\ket{b} = \bracket{a}{b} = (a_{0}b_{0}+a_{1}b_{1} )

行列（縦×横）　：　\ket{b}\bra{a} = \mtrx{b_{0}a_{0}}{b_{0}a_{1}}{b_{1}a_{0}}{b_{1}a_{1}}

正規直交基底

直交基底

$\ket{0},\ket{1}$はketなのでベクトルなのですが、どういったベクトルを割り当てるでしょうか？

|\psi〉 = \alpha\ket{0} + \beta\ket{1} \ \ \ \ \alpha ,\beta \in \mathbb{C_{複素数}}

上記の式は、$\ket{\psi}$という状態を、0になりそうな成分、1になりそうな成分 に成分分解し、その線形結合で量子状態を表現しようというものです。¹

係数である$\alpha,\beta$が同一の大きさのときに、0と1の重ね合わせ状態を表現できそうです。
成分分解ということで、$\ket{0},\ket{1}$は、x軸に対しy軸、実軸に対し虚軸、といったように直交したベクトルで表現するのが良さそうなので、下記とすることにしたいと思います。

\ket{0} =\tate{1}{0} \ \ \ \ \  \ket{1} =\tate{0}{1}

この2つの直交したベクトルは、$\ket{\psi}$の状態を成分分解できるという意味で直交基底という名前がついています。（他のペアもあるのでそれは後述します）³

内積と直交基底

内積を取ることで同一基底か直交基底を判断することができます。⁴

\bracket{0}{1} = \yoko{0}{1}\tate{1}{0}= 0

下記にパターンをまとめると

\displaylines{
\bracket{0}{1} = 0 \ \ \ \ \ \ \bracket{1}{0} = 0 　（直交）
\\
\bracket{0}{0} = 1 \ \ \ \ \ \ \bracket{1}{1} = 1 　（同一）
}

正規基底

基底のベクトルが単位ベクトル（長さ１）のものを正規基底と呼びます。
そして、直交基底で正規基底のものを正規直交基底と呼びます。
具体的には、$\ket{0},\ket{1}$は長さが１であるのは自明で、正規直交基底です。

\ket{x} = \tate{a}{b}　で　\bracket{x}{x} = (a^2 + b^2)

ですので、同一のベクトルで$\bracket{x}{x}$を計算すると長さが算出できます。
$\ket{0},\ket{1}$は上記で計算したとおり、内積が1となったので単位ベクトルであり正規直交基底です

パウリゲート

行列演算で考える

算数の授業でも１や２を覚えると、つぎに覚えるのは演算です。
$\ket{0}$と$\ket{1}$を用いた演算を考えてみたいのですが、単純に思いつくのは下記のような演算Uです。（反転操作）

\ket{0} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}　→　ある演算U　→　\ket{1} =  \begin{bmatrix} 0 \\ 1 \end{bmatrix}

$\ket{0}$や$\ket{1}$はベクトルですので、ベクトルに対しての演算（操作）を定義するには行列を利用するのが良さそうです。
そして、上記の「ある演算U」を実現する行列が、下記の行列Xです。

U = X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}

具体的に計算します。$\ket{0}$に対し、行列$X$を適用すると$\ket{1}$になりました。

X\ket{0} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \ket{1}

この行列（操作）には名前がついており、パウリのX（pauli-X) とか呼ばれたりします。
パウリ行列には、他にZ、Y等の別の操作を行える演算が存在します。（後述します）
そして、この操作の適用が、量子ビットに対するゲート適用に対応します。

braとketで考える

パウリの$X$を行列を用いて適用したのですが、$\ket{0}$や$\ket{1}$をベクトルや行列の表現にすることなく、パウリの$X$を適用する方法を検討してみたいと思います。
行列表現は理解しやすいのですが、今後、$\ket{00}$や$\ket{000}$等を扱うことを考えると、行列のサイズは指数関数的に大きくなるので、bra-ketに対する演算子としてのパウリ$X$を考えます。

\ket{0}　→　pauli X　→　\ket{1}

パウリの$X$は、上記を実現したいので、任意のケットに対して下記のように定義すれば良さそうです。

\ket{a}　→　pauli X　→　\ket{\bar{a}}

これを演算っぽく記述すると、下記のようになります

\displaylines{
X\ket{0} = \ket{1} \\ 
X\ket{1} = \ket{0} 
}

また、一般化するとこんな表記となります

X\ket{a} = \ket{\bar{a}} \ \ \ \ a \in \{0,1\}

パウリZ、Yも見てみる

先に結果を示すと、下記の通りとなります。
なお、一般化の$(-1)^{a}$に関しては、$a=0$の時、$(-1)^{0} = +1$となりマイナスがキャンセルされる仕掛けとなっています。

	bra-ket($\ket{0}\ket{1}$)を使って表現	一般化してみると($a \in {0,1}$)
$pauli$-$X$ bit-flip	$X\ket{0} = \ket{1}$ $X\ket{1} = \ket{0}$	$X\ket{a} = \ket{\bar{a}}$
$pauli$-$Z$ phase-flip	$Z\ket{0} = \ket{0}$ $Z\ket{1} = -\ket{1}$	$Z\ket{a} = (-1)^{a}\ket{a}$
$pauli$-$Y$ bit-flip + phase-flip + global-phase	$Y\ket{0} = i\ket{1}$ $Y\ket{1} = -i\ket{0}$	$Y\ket{a} = (-1)^{a}i\ket{\bar{a}}$

パウリ行列が示す事

変換操作（演算）が行列で示されてもなかなかムズカシイのですが、、、
パウリ行列をよく見るとある規則に気づきます。（スペースをあえて広めにとっています）

X = \begin{bmatrix}
 0 & 
 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 
 1 
 \\
 1 &
 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 
 0 \end{bmatrix}

X\ket{0} = \ket{1} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \ \ \ \ 
X\ket{1} = \ket{0} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}

$X$の1列目に、$\ket{0}$に$X$を適用した結果が現れる（$X\ket{0}$）
$X$の2列目に、$\ket{1}$に$X$を適用した結果が現れる（$X\ket{1}$）

つまり、イメージ的には下記の通りで、
行列を計算せずとも$\ket{0}$,$\ket{1}$にパウリゲートを適用した結果が、パウリ行列の中にそのまま現れていることが確認できます。

X = \begin{bmatrix} X\ket{0} & X\ket{1}  \end{bmatrix}

これは、パウリZ,Yでも同一で、
量子状態の観測結果を記述する基底（観測基底）として$\ket{0}$と$\ket{1}$を用いる限りにおいては、パウリゲート適用後の状態がパウリ行列で示されるので、ゲート適用に際し行列計算は不要です。

パウリZ

下記のような行列で示され、
パウリXと同様に$\ket{0}$,$\ket{1}$への適用結果がそのまま示されています。

Z = 
\begin{bmatrix}
 1 & 0 \\
 0 & -1 
\end{bmatrix}
\ \ \ \ \ \ \ \ \ 
Z = \begin{bmatrix} Z\ket{0} & Z\ket{1}  \end{bmatrix}

つまり、下記のようなオペレーションです。

$\ket{0}$にパウリZを適用しても、何もおきない
$\ket{1}$にパウリZを適用すると、符号が反転する(phase-flip)

パウリY

上述の通り、パウリYは下記のような行列で示されます。

Y = 
\begin{bmatrix}
 0 & -i \\
 i & 0 
\end{bmatrix}
\ \ \ \ \ \ \ \ \ 
Y = \begin{bmatrix} Y\ket{0} & Y\ket{1}  \end{bmatrix}

つまり、下記のようなオペレーションです。

$\ket{0}$にパウリZを適用すると、
- **ビットが反転（bit-flip)**する
- **iが付与（global-phase)**される　⁵
$\ket{1}$にパウリZを適用すると、
- **ビットが反転（bit-flip)**する
- **iが付与（global-phase)**される ⁵
- **符号も反転（phase-flip)**する（Zの符号反転も$\ket{1}$のみ）

ちょっと複雑ですが、パウリYは同時に３つの操作を行います。
数式で書くと下記のような関係性となります。

Y = iXZ

下記のような計算で確認できます

iXZ\ket{0} = iX\ket{0} = i\ket{1} = Y\ket{0} \\
iXZ\ket{1} = -iX\ket{1} = -i\ket{0} = Y\ket{1}

操作UのUとは

$pauli$-$XZY$と3つのパウリ行列を見てきましたが、３つの行列のは共通する点があります。
それは、ユニタリ行列（$U$）であるという点です。
ユニタリ行列とは、下記を満たす複素正方行列Uのことで、実数行列での直交行列に対応します。

U^{\dagger}U = UU^{\dagger} = E

$U^{\dagger}$は、実数行列における転置行列に対応するのですが、複素行列を対象とする場合には、複素数に対して複素共役とった複素転置（エルミート共役）の行列を指します。
具体的に、$pauli$-$XZY$について確認してみると、

\displaylines{

XX^{\dagger} = 
\begin{bmatrix}
 0 & 1 \\
 1 & 0 
\end{bmatrix}
\begin{bmatrix}
 0 & 1 \\
 1 & 0 
\end{bmatrix}
=
\begin{bmatrix}
 1 & 0 \\
 0 & 1 
\end{bmatrix}
=E

\\

ZZ^{\dagger} = 
\begin{bmatrix}
 1 & 0 \\
 0 & -1 
\end{bmatrix}
\begin{bmatrix}
 1 & 0 \\
 0 & -1 
\end{bmatrix}
=
\begin{bmatrix}
 1 & 0 \\
 0 & 1 
\end{bmatrix}
=E

\\

YY^{\dagger} = 
\begin{bmatrix}
 0 & -i \\
 i & 0 
\end{bmatrix}
\begin{bmatrix}
 0 & -i \\
 i & 0 
\end{bmatrix}
=
\begin{bmatrix}
 1 & 0 \\
 0 & 1 
\end{bmatrix}
=E
}

ちなみにゲートがユニタリーな必要がある。という話は「量子ゲートがユニタリーなわけ」でまとめていますので、よろしければこちらも参照ください。

まとめ

$pauli$-$XZY$の行列表現、$bra$-$ket$での表現を確認しました。再掲し下記に整理します。
本稿ではパウリゲートに慣れることを目的に下記の事項を扱っていない為、次回以降でまとめていこうと思います。
（更新：記事化しました。）

	bra-ket($\ket{0}\ket{1}$)を使って表現	一般化してみると($a \in {0,1}$)
$pauli$-$X$ bit-flip	$X\ket{0} = \ket{1}$ $X\ket{1} = \ket{0}$	$X\ket{a} = \ket{\bar{a}}$
$pauli$-$Z$ phase-flip	$Z\ket{0} = \ket{0}$ $Z\ket{1} = -\ket{1}$	$Z\ket{a} = (-1)^{a}\ket{a}$
$pauli$-$Y$ bit-flip + phase-flip + global-phase	$Y\ket{0} = i\ket{1}$ $Y\ket{1} = -i\ket{0}$	$Y\ket{a} = (-1)^{a}i\ket{\bar{a}}$

実際には、確率振幅（$\alpha,\beta \in \mathbb{C}$）の絶対値の2乗が観測確率となる ↩ ↩²
自由度の議論はこの記事ではあまり重要でないのですが、次回の記事でブロッホ球を見ていく段階で、必要となるのでここで触れておきます ↩
本稿で扱った計算基底($\ket{0}\ket{1}$)はZ軸上における正規直交基底で、これ以外にもX軸上のアダマール基底（$\ket{+},\ket{-}$)、Y軸上の円基底（$\ket{i+},\ket{i-}$）等がありますが、次回以降でブロッホ球と合わせて扱います。 ↩
bra⇔ketは、横ベクトル⇔縦ベクトルの変換ですが、$\alpha,\beta$が複素数ですので、転置時に複素共役を取る必要があります。$\bra{\psi} = (\ket{\psi})^{\dagger}$で、$\ket{\psi} = (\bra{\psi})^{\dagger}$となります。 ↩
グローバル位相（global-phase）については、ブロッホ球を扱ってから触れたほうが理解しやすいと思いますので、次回、触れていきたいと思います ↩ ↩²

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up