この記事について

アダマールテストと位相キックバックについて確認していきたいと思います。
なお、量子回路シミュレータのQuirkと数式両方を使って進めていこうと思います

また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。

\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}

アダマールテスト

比較的簡単な回路ではありますが、Controlled-Uゲートについて

制御ビット側には、Hゲートで重ね合わせ状態にした、$\ket{+}$を設定します
そして、標的ビット側には、ある状態ベクトル$\ket{\psi}$を設定します

Controlled-Uゲートは、CNOT等を想像いただくとわかるように、真理値表では制御ビットには変化がおきない様、定義がされていますが、制御ビットに重ね合わせを用いると、位相キックバックというおもしろい現象が発生するので見ていきたいと思います。

CNOT（Controlled-Not）のおさらい

上記のControlled-U（制御ユニタリ）の、Uの部分にXゲート（反転ゲート）を入れたのがCNOTです。

下記に示すとおり、

制御ビットの$\ket{0} \ket{1}$（on/off）に対応し、Controlled-U（Xゲート）が適用され標的が反転します。
制御ビットは、制御用なので、ゲート操作による変化は有りません

では、上述のように、制御ビット側がHゲートによる重ね合わせ（$\ket{+} = \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$になるとどうなるかを次に見ていきたいと思います。

標的ビット	制御ビットが$\ket{0}$	制御ビットが$\ket{1}$
$\ket{0}$
$\ket{1}$

制御ビットが重ね合わせ

上述のControlled-UのU、Zゲートを入れた状態で、制御ビットに重ね合わせを入れてみたいと思います。
（なぜ、Xでなく急にZなのかの理由は後述します）

標的ビットが、Zと|0>のとき

制御ビットは、重ね合わせの$\ket{+}$で入力し、標的ビットが$\ket{0}$のときは特に不思議なことはおきません。

標的ビットは、Z基底（$\ket{1}$）へのZゲート適用（Z軸回転）なので、適用の有無に関わらず変化なし
制御ビットは、制御に用いられるので、Controlled-Z前後で変化なし

Quirkでの量子回路へのリンク

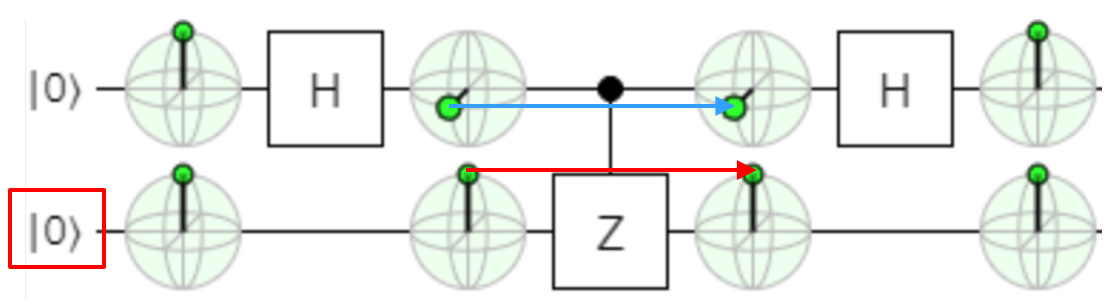
標的ビットが、Zと|1>のとき

標的ビットが$\ket{1}$にすると、制御ビット$\ket{+}$、Controlled-Uゲートの前後でに不思議な変化が起きます

標的ビットは、Z基底（$\ket{1}$）へのZゲート適用（Z軸回転）なので、適用の有無に関わらず変化なし
制御ビットは、Controlled-Z前後で、なんと、相対位相が変化しています（$\ket{+} → \ket{-}$）

これが、位相キックバック です。

Quirkでの量子回路へのリンク

整理すると

この回路に対して、ユニタリーとしてZ、入力ベクトル$\ket{\psi}$として$\ket{0}\ket{1}$を指定すると下記のような状態なりました。

$U$ゲート	$\ket{\psi}$	C-U直後の制御ビットの状態
$Z$	$\ket{0}$	$\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}\color{blue}{+1}\ket{1})$
$Z$	$\ket{1}$	$\ket{-}=\frac{1}{\sqrt{2}}(\ket{0}\color{blue}{-1}\ket{1})$

もう、お気づきの方もいらっしゃるかも知れませんが、

$Zゲート$に対して、$\ket{0}\ket{1}$、$+1,-1$は固有値、固有ベクトルの関係です。詳細は、こちらで
つまり、上記のアダマールテストの回路に対して、
- 任意のユニタリー$U$に対し、その固有ベクトル$\ket{\psi}$を入力すると
- 制御ビット側の$\ket{1}$の係数（相対位相）に、固有ベクトル$\ket{\psi}$での固有値が出現する
- 固有ベクトル$\ket{\psi}$を入力できれば、$U\ket{\psi}$を直接測定することなく$U$の固有値が得られる ¹
上記が、位相キックバックを用いた固有値の推定です¹

つまり他のパウリゲートについても整理すると下記のようになります

$U$ゲート	$\ket{\psi}$	$\ket{\psi}での固有値$	C-U直後の制御ビットの状態
$Z$	$\ket{0}$	$+1$	$\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}\color{blue}{+1}\ket{1})$
$Z$	$\ket{1}$	$-1$	$\ket{-}=\frac{1}{\sqrt{2}}(\ket{0}\color{blue}{-1}\ket{1})$
$X$	$\ket{+}$	$+1$	$\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}\color{blue}{+1}\ket{1})$
$X$	$\ket{-}$	$-1$	$\ket{-}=\frac{1}{\sqrt{2}}(\ket{0}\color{blue}{-1}\ket{1})$
$Y$	$\ket{i}$	$+1$	$\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}\color{blue}{+1}\ket{1})$
$Y$	$\ket{i-}$	$-1$	$\ket{-}=\frac{1}{\sqrt{2}}(\ket{0}\color{blue}{-1}\ket{1})$

最後に計算で確認しておきます

標的ビットが、Zと|0>のとき

Quirkでの量子回路へのリンク

$CZ_{12}$を適用した際に、$\ket{00},\ket{10}$と標的がいずれもゼロの為、$Z\ket{0}=\ket{0}$で変化しません

\displaylines{
\ket{00}
\xrightarrow[]{H_1}
\frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \otimes \ket{0} =\frac{1}{\sqrt{2}}(\ket{00} + \ket{10}) 
\\
\xrightarrow[]{\color{red}{CZ_{12}}}
\frac{1}{\sqrt{2}}(\ket{00} \color{red}{+} \ket{10}) = \frac{1}{\sqrt{2}}(\ket{0} \color{red}{+1} \ket{1}) \otimes \ket{0} 
}

標的ビットが、Zと|1>のとき

Quirkでの量子回路へのリンク

$CZ_{12}$を適用した際に、$\ket{01},\ket{11}$の為、$Z\ket{11}=\color{red}{-1}\ket{11}$と相対位相が変化します

\displaylines{
\ket{01}
\xrightarrow[]{H_1}
\frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \otimes \ket{1} =\frac{1}{\sqrt{2}}(\ket{01} + \ket{11}) 
\\
\xrightarrow[]{\color{red}{CZ_{12}}}
\frac{1}{\sqrt{2}}(\ket{01} \color{red}{-} \ket{11}) = \frac{1}{\sqrt{2}}(\ket{0} \color{red}{-1} \ket{1}) \otimes \ket{1} 
}

標的ビットが、Xと|+>のとき

Quirkでの量子回路へのリンク

\displaylines{
\ket{0+}
\xrightarrow[]{H_1}
\ket{++} =\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{0} + \ket{1})(\ket{0} + \ket{1})
\\
= \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} +\ket{01}+\ket{10}+\ket{11})
\\
\xrightarrow[]{\color{red}{CX_{12}}}
\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} +\ket{01}+ \color{red}{\ket{11}+\ket{10}})
\\
=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{0}  \color{red}{+1}\ket{1})(\ket{0} + \ket{1}) = \ket{++}
}

標的ビットが、Xと|->のとき

Quirkでの量子回路へのリンク

\displaylines{
\ket{0-}
\xrightarrow[]{H_1}
\ket{+-} =\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{0} + \ket{1})(\ket{0} - \ket{1})
\\
= \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00}-\ket{01}+\ket{10}-\ket{11})
\\
\xrightarrow[]{\color{red}{CX_{12}}}
\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} -\ket{01}+ \color{red}{\ket{11}-\ket{10}})
\\
=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{0} \color{red}{-1} \ket{1})(\ket{0} - \ket{1}) = \ket{--}
}

標的ビットが、Yと|i>のとき

Quirkでの量子回路へのリンク

\displaylines{
\ket{0i}
\xrightarrow[]{H_1}
\ket{+}\ket{i} =\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{0} + \ket{1})(\ket{0} + i\ket{1})
\\
= \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} +i\ket{01}+\ket{10}+i\ket{11})
\\
\xrightarrow[]{\color{red}{CY_{12}}}
\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} +i\ket{01}+ \color{red}{i\ket{11}-i^2\ket{10}})
\\
=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} +i\ket{01}+ \color{red}{\ket{10}+i\ket{11}})
\\
=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{0} \color{red}{+1} \ket{1})(\ket{0} + i\ket{1}) = \ket{+}\ket{i}
}

標的ビットが、Yと|i->のとき

Quirkでの量子回路へのリンク

\displaylines{
\ket{0i-}
\xrightarrow[]{H_1}
\ket{+}\ket{i-} =\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{0} + \ket{1})(\ket{0} - i\ket{1})
\\
= \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} -i\ket{01}+\ket{10}-i\ket{11})
\\
\xrightarrow[]{\color{red}{CY_{12}}}
\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} -i\ket{01}+ \color{red}{i\ket{11}--i^2\ket{10}})
\\
=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00} -i\ket{01}- \color{red}{\ket{10}+i\ket{11}})
\\
=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{0} \color{red}{-1} \ket{1})(\ket{0} - i\ket{1}) = \ket{-}\ket{i-}
}

制御側の相対位相にキックバックされる固有値の表現

パウリゲートの場合、制御側の相対位相にキックバックされる固有値は、$+1,-1$ですが一般的なユニタリーに対してはどのように表現されるべきでしょうか？
実を言うと、

ユニタリー行列の固有値（$\lambda$）の絶対値は、$|\lambda|^2=1$ となることが知られています。
複素平面で絶対値が１となりそうな便利なものはなんでしょう？そうです。 $e^{i\theta}$です。

|e^{i\theta}|^2 = 1 \ \ \ \ \ \ \ \because e^{i\theta} = cos\theta + isin\theta

よって、$\ket{+}$の相対位相にキックバックされる固有値は下記のように表現されることが多いです。

Control \ qubit = \frac{1}{\sqrt{2}}(\ket{0} + \color{red}{e^{i\lambda}}\ket{1})

まとめ

アダマールテストでの位相キックバックについて、パウリゲートの固有値と固有ベクトルを使い、固有値が制御ビット側にどのようにキックバックされるかを確認してみました。¹
この位相キックバックを連鎖的に適用し、その結果を量子逆フーリエ変換（$QFT^{\dagger}$）することで、kitaevの量子位相推定（$QPE$）アルゴリズムを構築できます。
この、$QFT,QPE$については、アドベントカレンダーの明日の記事にて説明予定ですので、ご確認いただければと思います。

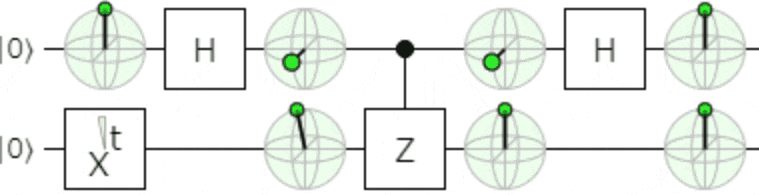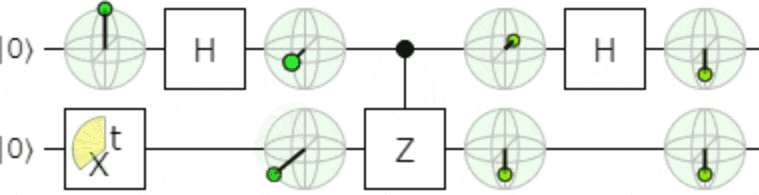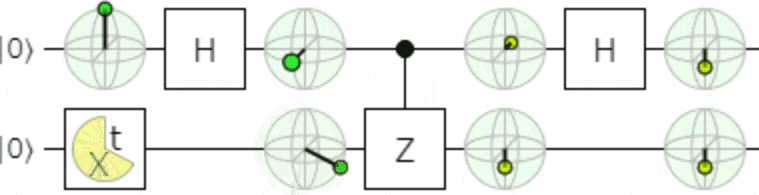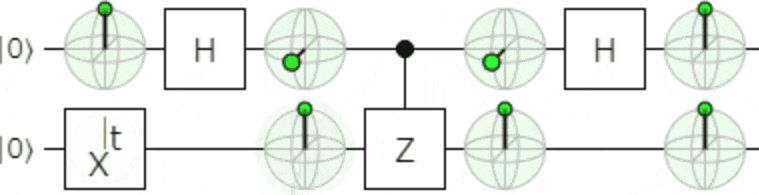
おまけ

アニメーションにすると、制御ビット側の相対位相が変化するのがよく分かると思いますので、
こんなものを添付しておきます。

Quirkでの量子回路へのリンク

参考資料

下記を参考にさせて頂きました

実際には複数回観測して、確率的に固有値を得るので、複数回の実行もしくはkitaevの量子位相推定アルゴリズムのような工夫が必要です。反復回数が誤差($\epsilon$)に対して、$O(1/\epsilon)$程度で済む点が最大のメリットなのですが、この点は次回の量子位相推定で触れていこうと思っています。 ↩ ↩² ↩³