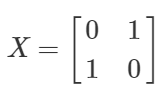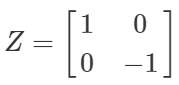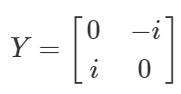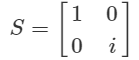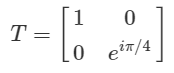ブロッホ球と各種ゲートの関係

この記事について

前回は、下記でパウリゲートを見てきましたが、今回は量子状態の表現方法であるブロッホ球を扱います

上記では触れることができなかった下記３点についてまとめてみたいと思います。

• ブロッホ球と計算基底( |0> |1> )以外の正規直交基底
• ブロッホ球と各ゲート（$X,Y,Z,H,S,T$）の関係（回転）

また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。

\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}

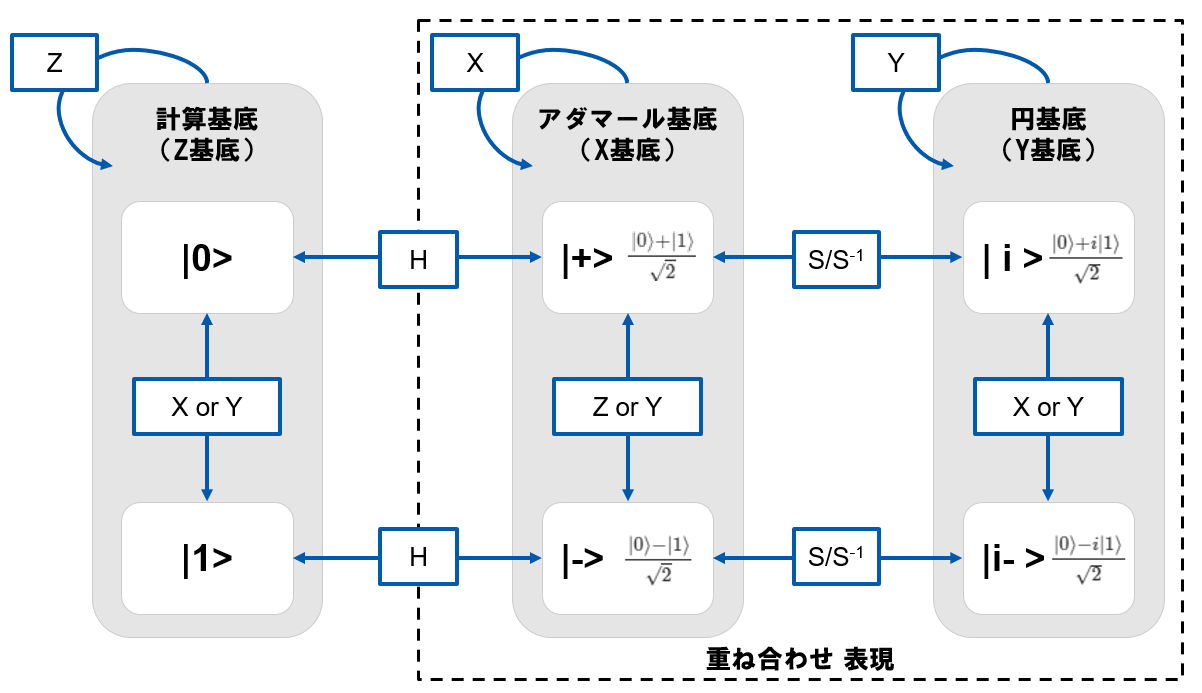
ブロッホ球と正規直交基底

量子状態の表現

以前の記事でも触れたように、重ね合わせ状態を表現するために下記のように表現します。

|\psi〉 = \alpha\ket{0} + \beta\ket{1}\ \ \ \ \alpha ,\beta \in \mathbb{C_{複素数}} 

α,βは複素数で実部、虚部があるため自由度は4となります。

\displaylines{
\alpha = a_{①実部} + a_{②虚部}i \\
\beta  = b_{③実部} + b_{④虚部}i
}

ただし、規格化条件により下記を満たす必要があり、この束縛で自由度は3となります。

|\alpha|^2 + |\beta|^2 = 1

上記の規格化条件により、量子の状態ベクトル( $\ket{\psi}$ )の長さは常に１となります。
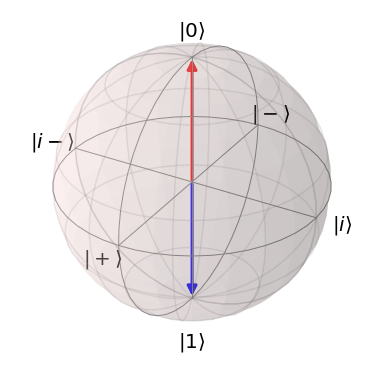
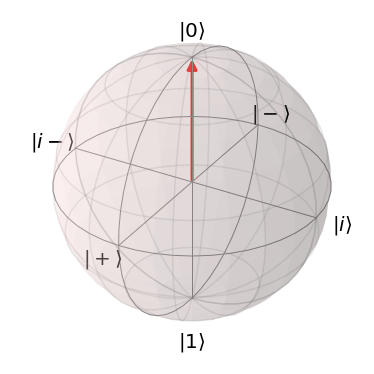
自由度３ということで３次元空間があれば、状態ベクトルが可視化できそうというのがブロッホ球のアイディアです。具体的には下記のような見た目となります。¹

ブロッホ球

これまで扱ってきた計算基底（$\ket{0}\ket{1}$)をZ軸上に配置されます。Z軸上に存在する背景からZ基底とも呼ばれます。

なお、先程から議論がある$\ket{0}\ket{1}$の重ね合わせ状態は、$\ket{\psi}$ がX-Y平面上の円周（破線）上に存在するときに、同確率で重ね合わせになっている状態となります。
下記はWikipediaより引用しています。¹

単位円（球）上に、状態ベクトル( $\ket{\psi} $ )が存在する状況を、三角関数を用いて下記のように表現します。

\ket{\psi} = e^{i\gamma} \left(cos\dfrac{\theta}{2}\ket{0} + e^{i\varphi}sin\dfrac{\theta}{2}\ket{1} \right)

ちょっとムズカシイ式なので、分解して部分毎に意味を解釈していきましょう。
注意点としてはパラメータ３つのうち$\theta$は$1/2$が掛かっている為、$\theta$に関しては１回転が、$4\pi$となります。

複雑な数式ですが３つ（青、赤、緑）のパートに分解し、理解を進めたいと思います。

\ket{\psi} = \color{green}{e^{i\gamma}} \color{blue}{\left(cos\dfrac{\theta}{2}\ket{0} + \color{red}{e^{i\varphi}}sin\dfrac{\theta}{2}\ket{1} \right)} 

①Z軸方向（垂直方向）

Z軸方向の制御ですが、②③が1の時( $\color{green}{e^{i\gamma}} =\color{red}{e^{i\varphi}} = 1)$下記のように表現できます。
$\theta/2$という部分は特殊ですが、単位円を描く事ができる数式で、$\theta$を用いてZ軸に対する方向を制御することで、重ね合わせ状態での0と1の存在確率を制御できます。

①Z軸方向の制御\ = \color{green}{1} × \color{blue}{\left(cos\dfrac{\theta}{2}\ket{0} + \color{red}{1}×sin\dfrac{\theta}{2}\ket{1} \right) \\= cos\dfrac{\theta}{2}\ket{0} + sin\dfrac{\theta}{2}\ket{1}}

②XY平面（水平方向）

XY平面は$e^{i\varphi}$を複素平面に対応させると、こちらもやはり単位円を描く事ができます。
XY平面（水平方向）での状態ベクトルの位置を制御します。

②XY平面の制御\ = \color{red}{e^{i\varphi} = cos\ \varphi + i\ sin\ \varphi \\}

③全体に係る係数（位相）

式全体に係る$e^{i\varphi}$ですが、こちらはブロッホ球上には表現されません。
式全体に係る位相であるため、グローバル位相(global phase)という名前もついているようです。

③式全体に係る係数\ = \color{green}{e^{i\gamma} = cos\ \gamma + i\ sin\ \gamma}

正規直交基底に対して各種ゲート操作を適用すると、式でくくり出しが可能な式全体に係る下記のような係数が出現します。

+1,+i,-1,-i 

計算結果の観測は$\ket{0},\ket{1}$の相対的な関係を観測する背景で、式全体に係る係数（位相）は、量子状態の観測結果には直接影響を与えない（観測できない）ので意識する必要は無いのですが、観測前の量子状態としてはグローバルな位相が内在するはずですので、数理モデル（ブロッホ球）上は必要となるため、数式上現れています。

なお、グローバル位相については、「ブロッホ球のグローバル位相について」にまとめています。

各パラメータと正規直交基底の関係

各パラメータの意味と、正規直交基底との対応をまとめると下記のとおりとなります。
なお、$\ket{+}\ket{-}\ket{i}\ket{i-}$については、次項で説明します。

パラメタ	ブロッホ球上の意味	正規直交基底との対応
$\theta$	Z軸に対する角度	$\ket{0}の時、\theta = 0$ですが、 $\ket{1}の時、\theta = 2\pi$（注意）
$\phi$	X-Y平面での X軸に対する角度	$\ket{+}の時、\varphi = 0$ $\ket{-}の時、\varphi = \pi$ $\ket{i}\ \ の時、\varphi = \pi/2$ $\ket{i-}の時、\varphi = 3\pi/2$
$\gamma$	グローバル位相 ※ブロッホ球上現れない	正規直交基底に対しくくり出せる 状態ベクトル全体への係数として存在

ブロッホ球上の正規直交基底

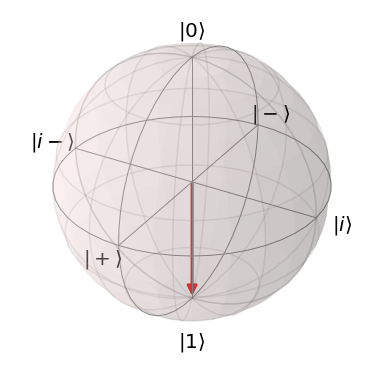
計算基底（Z基底）

計算基底はZ軸上に存在するのでZ基底とも呼ばれます、下記の左が$\ket{0}$で、右が$\ket{1}$となります。

$\ket{0}$	$\ket{1}$

X軸、Y軸上の正規直交基底

$\ket{0}と\ket{1}$ の重ね合わせは、水平方向（X-Y）平面で表現されるのですが、代表的な４点について紹介しておきます。

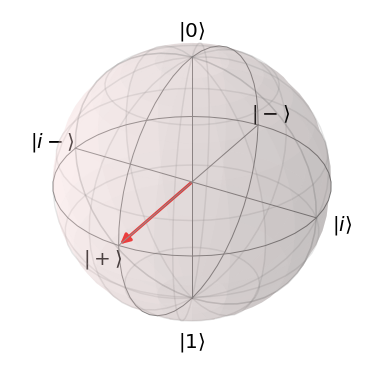
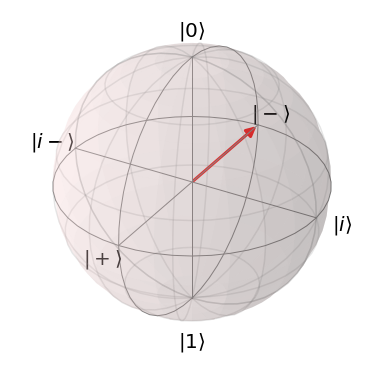
アダマール基底（X基底）

X軸方向に存在するのが、アダマール基底（$\ket{+}\ket{-}$)で、計算基底（$\ket{0}\ket{1}$)に対して後述するH（アダマール）ゲートを適用すると、この状態となります。

$\ket{+}=\frac{\ket{0}+\ket{1}}{\sqrt{2}}$	$\ket{-}=\frac{\ket{0}-\ket{1}}{\sqrt{2}}$

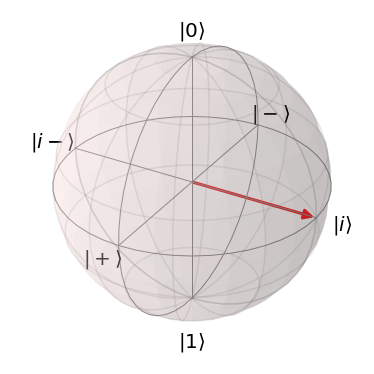
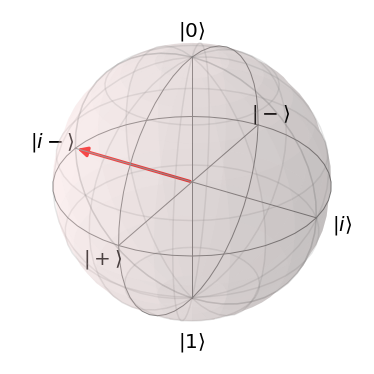
円基底（Y基底）²

Y軸方向に存在するのが、円基底（$\ket{i}\ket{i-}$)で、アダマール基底（$\ket{+}\ket{-}$）に対して、X-Y平面で90度($\pi/2$)回転したものがそれぞれ$\ket{i}\ket{i-}$です。

$\ket{i}=\frac{\ket{0}+i\ket{1}}{\sqrt{2}}$	$\ket{i-}=\frac{\ket{0}-i\ket{1}}{\sqrt{2}}$

ブロッホ球とパウリゲート

「重ね合わせ無し」でのゲート適用

「重ね合わせ」がない状態では、状態ベクトルはZ軸上にのみ存在する為、利用する基底は計算基底(Z基底)のみとなります。

この記事で整理させて頂いたとおり、パウリゲート（XZY）下記の操作となります。

	行列で表現	bra-ket($\ket{0}\ket{1}$)を使って表現	一般化してみると($a \in {0,1}$)
$pauli$-$X$ bit-flip		$X\ket{0} = \ket{1}$ $X\ket{1} = \ket{0}$	$X\ket{a} = \ket{\bar{a}}$
$pauli$-$Z$ phase-flip		$Z\ket{0} = \ket{0}$ $Z\ket{1} = -\ket{1}$	$Z\ket{a} = (-1)^{a}\ket{a}$
$pauli$-$Y$ bit-flip + phase-flip + global-phase		$Y\ket{0} = i\ket{1}$ $Y\ket{1} = -i\ket{0}$	$Y\ket{a} = (-1)^{a}i\ket{\bar{a}}$

パウリゲートのうち、$\ket{0}→\ket{1}、\ket{1}→\ket{0}$と、反転が行えるゲートは$XとY$です。
具体的には、下記の演算となります。
Yゲートでは、$i,-i$等が付きますが、後ほど説明しますので、一旦、計算基底は反転している事実を理解してください。

\displaylines{
X\ket{0} = 1 × \ket{1}\\
Y\ket{0} = i × \ket{1}\\
X\ket{1} = 1 × \ket{0}\\
Y\ket{1} = -i × \ket{0}
}

なぜ、パウリ$X,Y$がZ基底（$\ket{0},\ket{1}$）を反転できるか？というと、実を言うと、パウリ$X,Y$はそれぞれブロッホ球上でのX軸、Y軸を中心とした$\pi(180^{\circ})$回転を意味します。アニメーションにするとこんなイメージです。

パウリX（X軸を中心にπ回転）

$X\ket{0} = \ket{1}$	$X\ket{1} = \ket{0}$
$\ket{0}$から$X$軸を中心に$\pi$回転し、$\ket{1}$に	$\ket{1}$から$X$軸を中心に$\pi$回転し、$\ket{0}$に

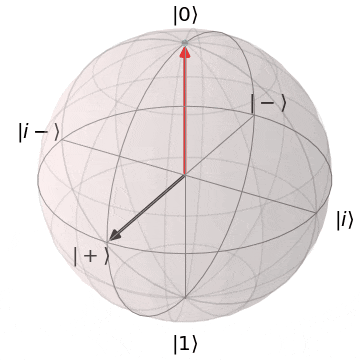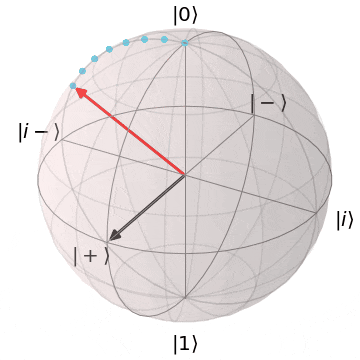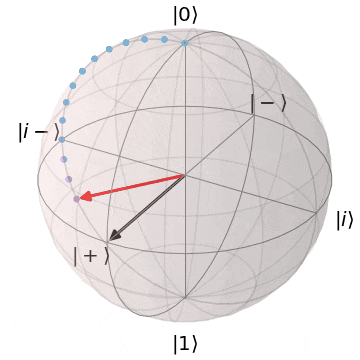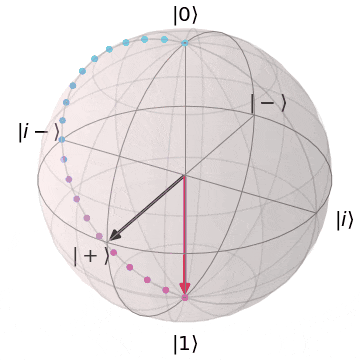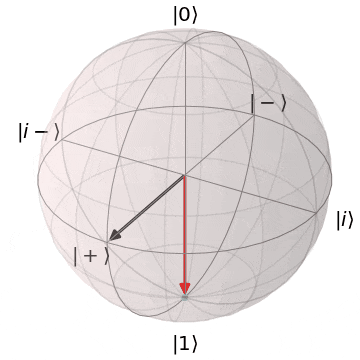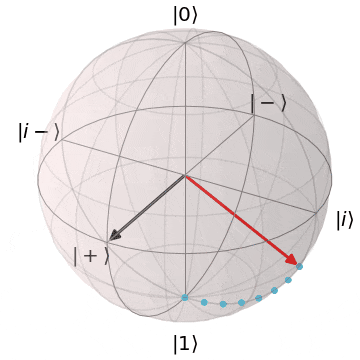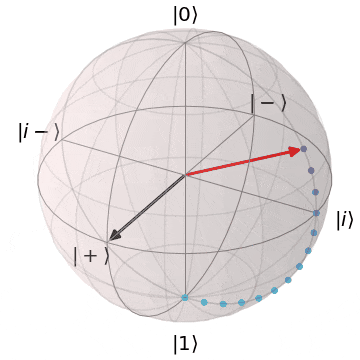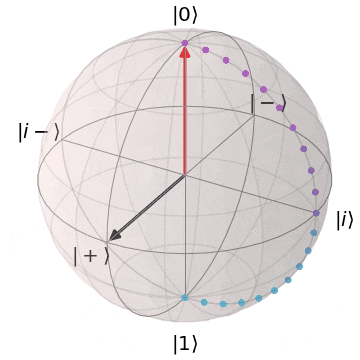パウリY（Y軸を中心にπ回転）

$Y\ket{0} = i\ket{1}$	$Y\ket{1} = -i\ket{0}$
$\ket{0}$から$Y$軸を中心に$\pi$回転し、$\ket{1}$に	$\ket{1}$から$Y$軸を中心に$\pi$回転し、$\ket{0}$に

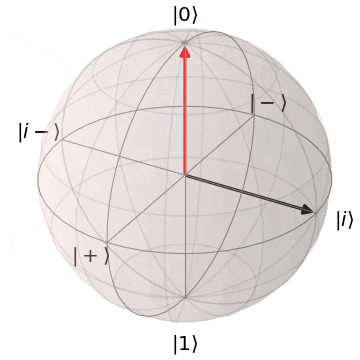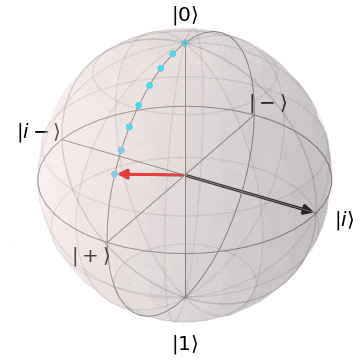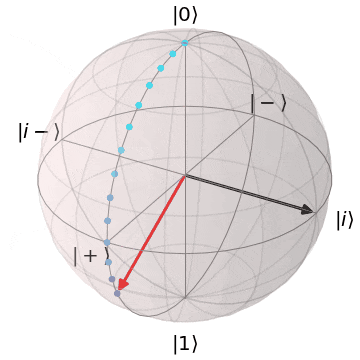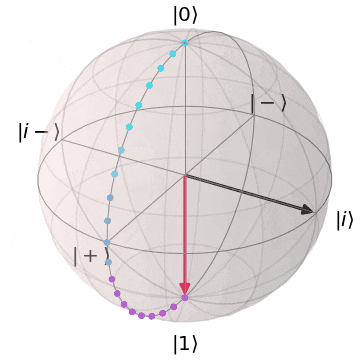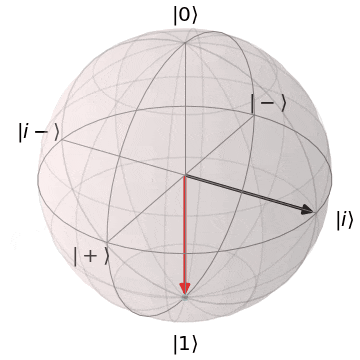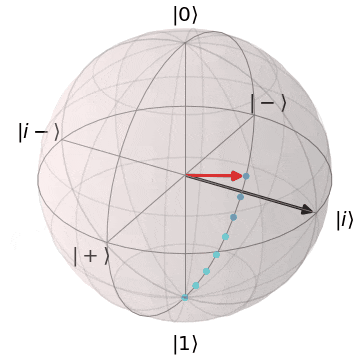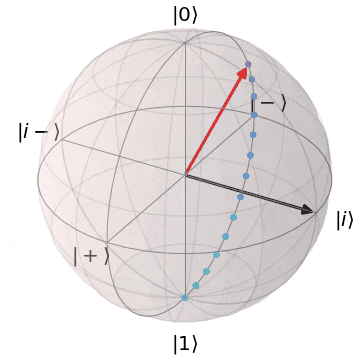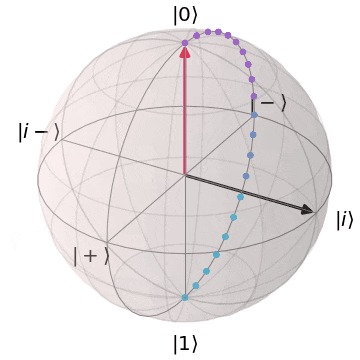パウリZ（Z軸を中心にπ回転）

$Z\ket{0} = \ket{0}$	$Z\ket{1} = -\ket{1}$
$\ket{0}$から$Z$軸を中心に$\pi$回転し、$\ket{0}$に Z軸回転しても結果変わらず	$\ket{1}$から$Z$軸を中心に$\pi$回転し、-$\ket{1}$に Z軸回転しても結果変わらず

回転するもの、しないもの

ブロッホ球上では、パウリゲートの適用は回転として扱えることを見てきました。

• $Z$基底（計算基底の$\ket{0},\ket{1}$)に対して、パウリ$X,Y$は$\pi$回転した。
• $Z$基底 に対して、パウリ$Z$は変化無し。

という結果となりました、パウリゲートの適用を回転として扱うと、その回転軸上の正規直交基底は、位相以外は変化しませんでした。
これは、他のX基底、Y基底でも成り立つ事実で、

• 基底と同一の軸のパウリゲートは、状態ベクトルを変化させない　（位相以外）
• 基底と異なる軸のパウリゲートは、状態ベクトルを変化させる

という整理ができます。

「重ね合わせなし」での基底とパウリゲートの関係性

Z基底に関しては、Zゲートは変化なし、XYゲートは$\ket{0} \leftrightarrow\ket{1}$と反転するので整理すると下記のような状況となります。

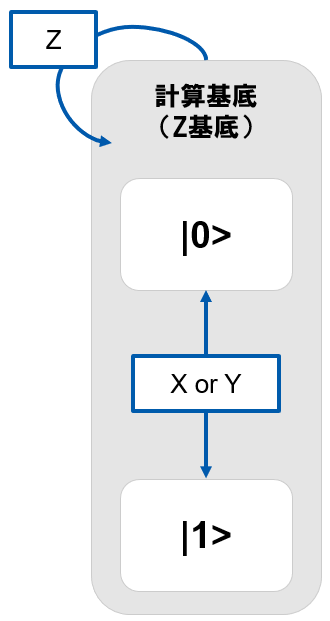
「重ね合わせ有り」でのゲート適用

アダマール（H）ゲートと重ね合わせ

今までは、状態ベクトルがZ軸上のみで、重ね合わせがない状態でしたが重ね合わせを考慮していきます。
状態ベクトルの表現を再度見直すと下記のとおりで、$\ket{0}と\ket{1}$の重ね合わせ状態を作るのですが、
アダマール($H$)ゲートが必要となるのでここで導入します

|\psi〉 = \alpha\ket{0} + \beta\ket{1}\ \ \ \ \alpha ,\beta \in \mathbb{C_{複素数}} 

アダマール(H)ゲート

さきにパウリと同様に$H$ゲートの各表現をしめしておきます。

	行列で表現	bra-ketを使って表現	一般化してみると($a \in {0,1}$)
$Hadamard$ superposition		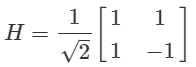$H\ket{0} = \ket{+}$ $H\ket{1} = \ket{-}$	$H\ket{a} = \frac{1}{\sqrt{2}}\sum_{b=0,1}(-1)^{ab}\ket{b}$

まずは、行列表現について見て行きたいと思います。

\displaylines{
H\ket{0} = \frac{1}{\sqrt{2}}\mtrx{1}{1}{1}{-1}\tate{1}{0} = \tate{\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}} \\
\leftrightarrow \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1}  = \ket{+} 
}

一般化された表現も見ていきます。
こちらは$\ket{1}$の時がチョット複雑なので、両方計算しておきたいと思います。
$\ket{0}$の時は、マイナスが$(-1)^{0 \times b}$でキャンセルされます。

H\ket{0} = \frac{1}{\sqrt{2}}\sum_{b=0,1}(-1)^{0 \times b}\ket{b} =  \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) = \ket{+}

$\ket{1}$の時は、マイナス部分が$(-1)^{b}$となり、$b=1$の時のみマイナスとなる仕掛けです

H\ket{1} = \frac{1}{\sqrt{2}}\sum_{b=0,1}(-1)^{b}\ket{b} =  \frac{1}{\sqrt{2}}((-1)^{0}\ket{0} + (-1)^{1}\ket{1}) = \ket{-}

ブロッホ球上でのアダマールゲート

アダマール（$H$）ゲートは、X,Z軸のちょうど中間（$45^{\circ}$）を回転軸として、$\pi(180^{\circ})$回転します。
詳細は、下記ご確認ください。

その結果、

• $\ket{0} \rightarrow \ket{+}$
• $\ket{1} \rightarrow \ket{-}$

といったように、
Z基底とX基底間の移動を行い、X基底上の重ね合わせ状態($superposition$)に移行します。

$H\ket{0} = \ket{+}$	$H\ket{1} = \ket{-}$
$\ket{0}$から$\ket{+}$に	$\ket{1}$から$\ket{-}$に

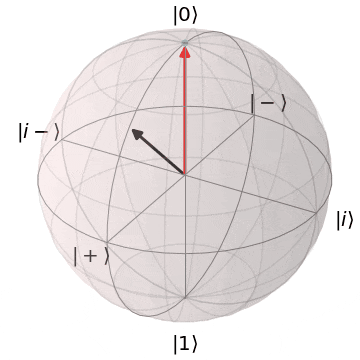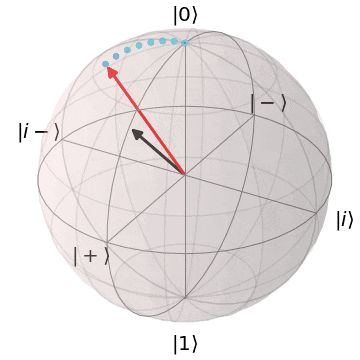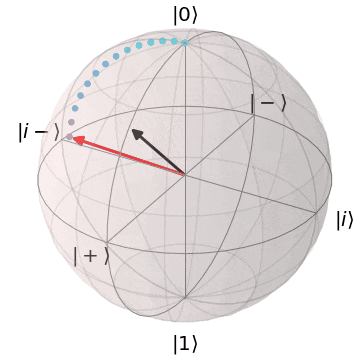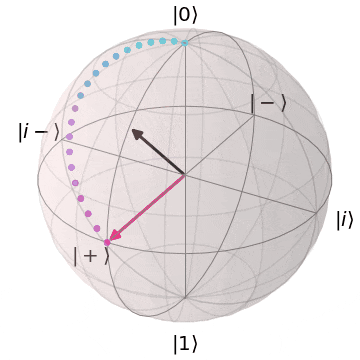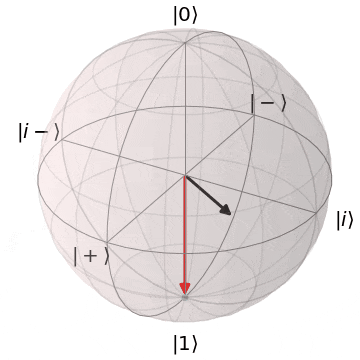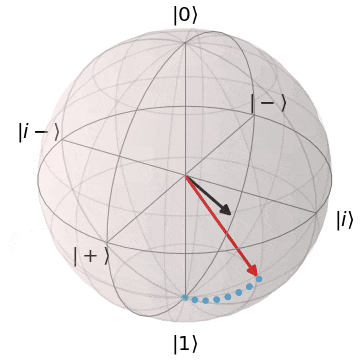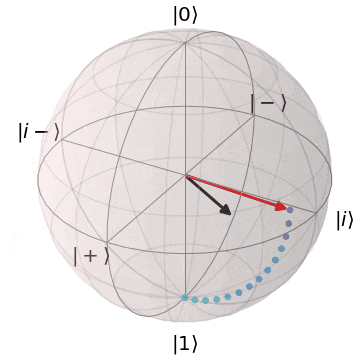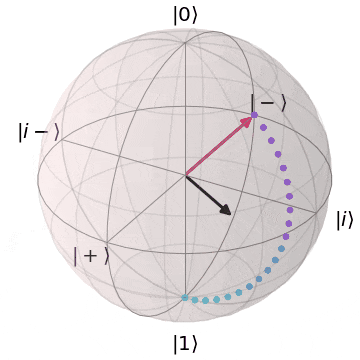「重ね合わせあり」での基底とパウリゲートの関係性

$Z$基底($\ket{0}\ket{1}$)の状態ベクトルに$H$ゲートを適用すると、$X$基底（$\ket{+}\ket{-}$）に移行するため、先程の関係図に右部分を追加しました。
$X$基底内に関しては、$Z$基底と同様に同一軸（$X$ゲート）の適用では状態は変化せず、$X$以外の$Y,Z$ゲートが、$X$基底内で状態を$\ket{+} \leftrightarrow \ket{-}$と変化させます。

Y基底への到達方法

$Z$基底($\ket{0}\ket{1}$)から、$X$基底（$\ket{+}\ket{-}$）は$H$ゲートで到達できましたが、$Y$基底（$\ket{i},\ket{i-}$）へはどのように到達すれば良いでしょうか？
$X$基底（$\ket{+}\ket{-}$）から水平方向（Z軸を中心）に、$\pi/2(90^{\circ})$回転させれば$Y$基底（$\ket{i},\ket{i-}$）に到達しますが、Z軸を中心に回転する$Z$ゲートの回転は$\pi(180^{\circ})$であるため、$Z$ゲートの半分の回転が必要となります。
そこで、回転角が$1/2$や$1/4$のゲートを導入します。

S,Tゲート

さきにアダマールと同様に$S,T$ゲートの各表現をしめしておきます。

	行列で表現	bra-ketを使って表現	一般化してみると($a \in {0,1}$)
$S$-$gate$		$S\ket{+} = \ket{i}$ $S\ket{-} = \ket{i-}$	$S\ket{a} = (i)^{a}\ket{a}$
$T$-$gate$		$T^{2}\ket{+} = \ket{i}$ $T^{2}\ket{-} = \ket{i-}$	$T\ket{a} = (e^{i\pi/4})^{a}\ket{a}$

計算を確認しておきます。

\displaylines{
S\ket{+} = \mtrx{1}{0}{0}{i}\tate{\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}} = \tate{\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}i} \\
\leftrightarrow \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}i\ket{1}  = \ket{i}
}

Tに関して2乗して、Sになることを確認します。

T^2 = \mtrx{1}{0}{0}{e^{i\pi/4}}\mtrx{1}{0}{0}{e^{i\pi/4}} = \mtrx{1}{0}{0}{e^{i\pi/2}}

$e^{i\pi/2}$は複素平面では下記となり、$i$となるのでSと一致します

e^{i\pi/2} = cos\frac{\pi}{2} + i\ sin\frac{\pi}{2} = i \ \ \ \  \therefore T^2 = \mtrx{1}{0}{0}{i} = S  

同様に、一般化された式の方も確認しておきます。

\displaylines{
S\ket{+} = \frac{1}{\sqrt{2}} S(\ket{0} + \ket{1}) = \frac{1}{\sqrt{2}} ((i)^{0}\ket{0} + (i)^{1}\ket{1} = \ket{i}
\\
T^{2} = ((e^{i\frac{\pi}{4}})^{a})^2\ket{a} = (e^{i\frac{\pi}{4}\times2})^{a}\ket{a} =(e^{i\frac{\pi}{2}})^{a}\ket{a} = (i)^{a}\ket{a} = S
}

Z軸を中心とした回転ということで、$Z,S,T$の関係を整理しておくと下記となります。

S^{2} = ((i)^a)^2\ket{a} = ((i)^2)^a\ket{a} = (-1)^a\ket{a} = Z

よって、

\therefore Z = S^{2} = T^{4}

ブロッホ球上でのS,Tゲート

Sゲート

$S\ket{+} = \ket{i}$	$S\ket{-} = \ket{i-}$
$\ket{+}$から$Z$軸を中心に$\pi/2$回転し、$\ket{i}$に	$\ket{-}$から$Z$軸を中心に$\pi/2$回転し、$\ket{i-} $に

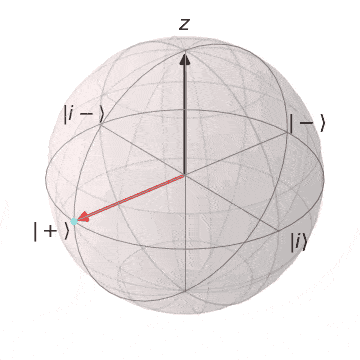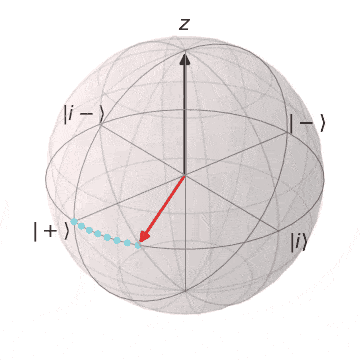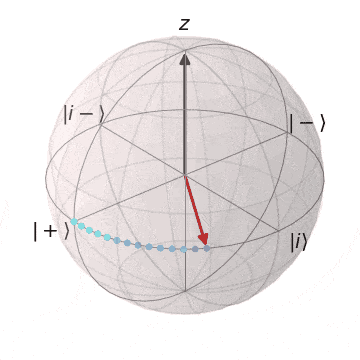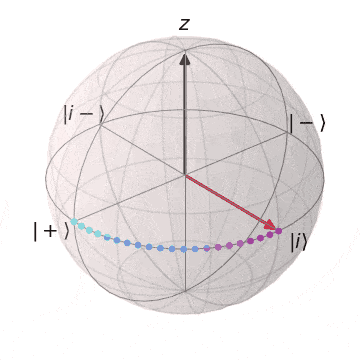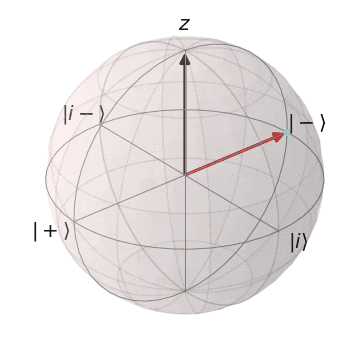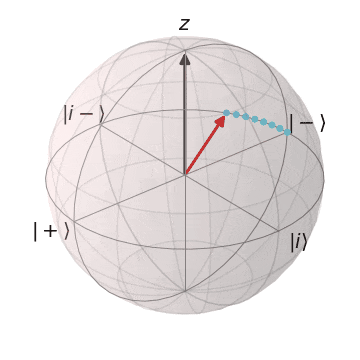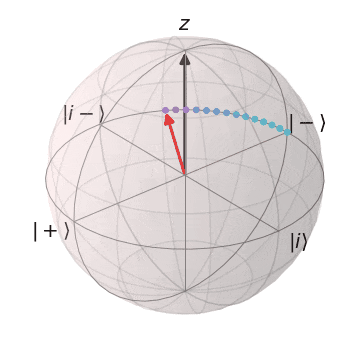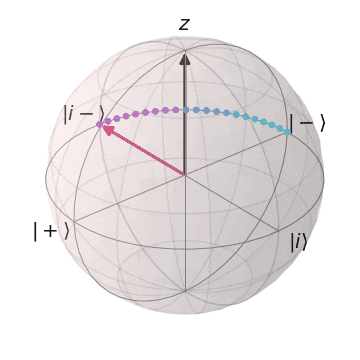Tゲート

$T\ket{+}$	$T\ket{-}$
$\ket{+}$から$Z$軸を中心に$\pi/4$回転	$\ket{-}$から$Z$軸を中心に$\pi/4$回転

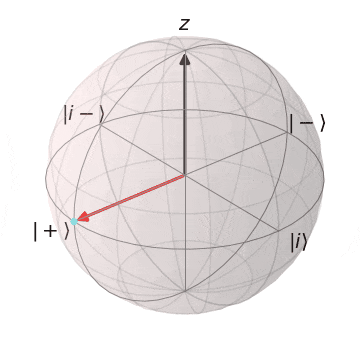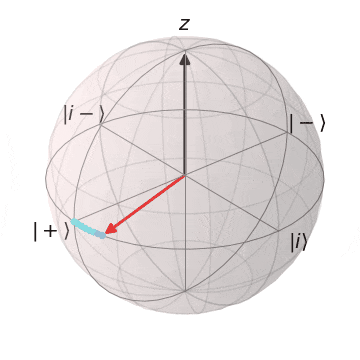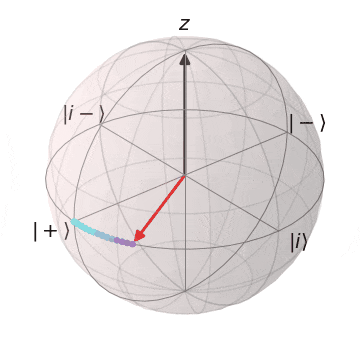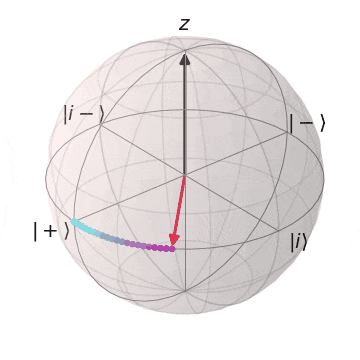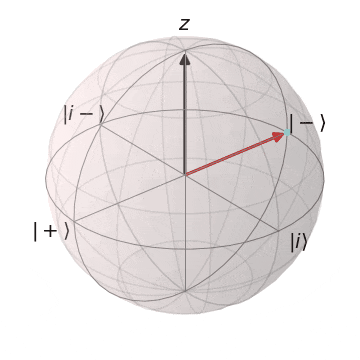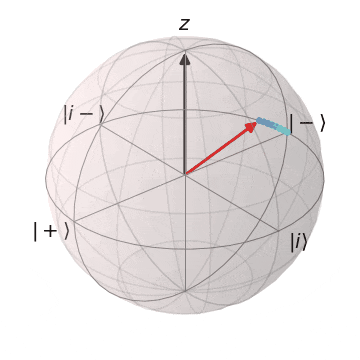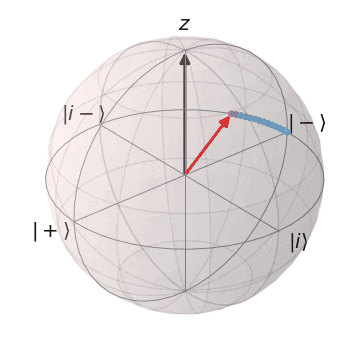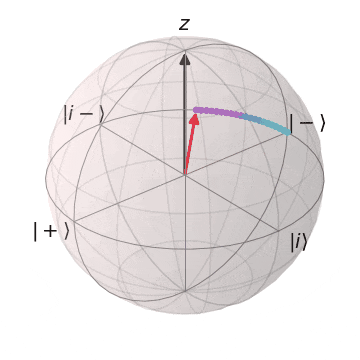各種基底とパウリゲートの関係性

$S,T$ゲートを導入することで、$X$基底($\ket{+}\ket{-}$)から$Y$基底($\ket{i}\ket{i-}$)に到達できました。
最後にこれまでの各種基底とゲートの関係性をまとめると下記となります。
$Z$基底は重ね合わせがない状態、$X,Y$基底は重ね合わせ状態であり、$H$ゲートが重ね合わせにおいて重要な役割を担っている事がわかります。

まとめ

本稿では、正規直交基底（$X,Y,Z$基底）の説明と各種ゲートがどのように作用するかを、ブロッホ球をぐるぐるしながら整理しました。

• グローバル位相については、重ね合わせ状態（$X,Y$基底）に対してパウリゲートを適用する計算をすると、$\ket{0}と\ket{1}$の相対的な関係には影響を及ぼさない（式としてくくり出せる）係数が出現し、ブロッホ球の数式表現として必要であることが理解できるので、次回以降で確認していこうと思います。

  • 記事化しました　→　ブロッホ球のグローバル位相について

• また、本稿で基本ゲートはすべて導入したので残りは、回転ゲート($Rx,Ry,Rz$)と、Cnot等の$controled-U$ゲートとなります。これも別途、まとめる予定です。

• その後に、量子テレポーテーションや超高密度符号化実験等もやれれば良いと考えています。

（記事化しました）

長文となりましたが、お付き合いありがとうございます。

1. https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%AD%E3%83%83%E3%83%9B%E7%90%83 より引用 ↩ ↩²

2. Circular Basis ↩