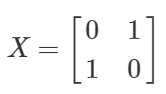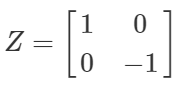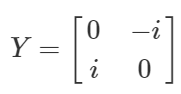ブロッホ球とグローバル位相について

この記事について

下記の記事で、正規直行基底、パウリゲート、ブロッホ球についての導入が終わったので、ブロッホ球のグローバル位相について考えてみたいと思います。

• パウリゲート（XZY）を細かく見てみる
• ブロッホ球と各種ゲートの関係

下記の順で議論を進めていきたいと思います。

• ブロッホ球の数式表現について振り返り
• 正規直交基底（$X,Y,Z基底$）についてパウリゲートを適用する計算と結果の確認
• その計算結果からグローバル位相というものが必要そうだ、という主張を導出する

この記事は正直あまり自信が無いのですが現状の自分の理解を整理したものですので、ぜひ、コメントいただける方はコメントを頂ければ幸いです。

また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。

\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}

素朴な疑問

ブロッホ球

ブロッホ球については、こちらで記述しておりますので、ご確認ください。
下記はWikipediaより引用しています。¹

数式表現は下記の通りです。

\ket{\psi} = \color{red}{e^{i\gamma}} {\left(cos\dfrac{\color{blue}{\theta}}{2}\ket{0} +{e^{i\color{blue}{\varphi}}}sin\dfrac{\color{blue}{\theta}}{2}\ket{1} \right)} 

なぜグローバル位相が必要？

パラメータのうち

• $\color{blue}{\theta,\varphi}$は、ブロッホ球上も可視化されますし、量子状態（$\ket{\psi}$）にも影響を及ぼします。
• $\color{red}{e^{i\gamma}}$（グローバル位相）はブロッホ球上も現れず、量子状態（$\ket{\psi}$）にも影響を与えません。

量子状態（$\ket{\psi}$）の観測結果に影響を与えないのは、重ね合わせを含めた量子状態の観測は$\ket{0}と\ket{1}$の相対的な関係を観測し、かつ、観測する確率は確率振幅の２乗となるため、式全体に係る係数（位相）は観測結果には無影響というのは理解できるのですが、であれば、数式上のこの係数はなぜ定義されているのかが疑問になります。その点について少し考察してみたいと思います。

振り返り

導入済みのゲート

詳細はこちらをご確認ください。

	行列で表現	bra-ket($\ket{0}\ket{1}$)を使って表現	一般化してみると($a \in {0,1}$)
$pauli$-$X$ bit-flip		$X\ket{0} = \ket{1}$ $X\ket{1} = \ket{0}$	$X\ket{a} = \ket{\bar{a}}$
$pauli$-$Z$ phase-flip		$Z\ket{0} = \ket{0}$ $Z\ket{1} = -\ket{1}$	$Z\ket{a} = (-1)^{a}\ket{a}$
$pauli$-$Y$ bit-flip + phase-flip + global-phase		$Y\ket{0} = i\ket{1}$ $Y\ket{1} = -i\ket{0}$	$Y\ket{a} = (-1)^{a}i\ket{\bar{a}}$

導入済みの正規直交基底

詳細はこちらをご確認ください。

名称	+	-
$Z$基底	$\ket{0}$	$\ket{1}$
$X$基底	$\ket{+}=\frac{\ket{0}+\ket{1}}{\sqrt{2}}$	$\ket{-}=\frac{\ket{0}-\ket{1}}{\sqrt{2}}$
$Y$基底	$\ket{i}=\frac{\ket{0}+i\ket{1}}{\sqrt{2}}$	$\ket{i-}=\frac{\ket{0}-i\ket{1}}{\sqrt{2}}$

早速、計算

下記のチャートに従い、実際に各正規直交基底にゲート適用した際に、このフロー図通りとなるかを確認してみたいと思います。このチャートに関してはこちらをご確認ください。

Z基底

Z基底の計算は比較的簡単なのでまとめていきます。
というか、パウリ行列がそのまま現れるので、計算では無いですね。。
注目頂きたいのは、ゲート適用で$\color{red}{1,-1,i,-i}$が現れる点です

Xゲート

X\ket{0} = \ket{1} \ \ \ \ \ \  X\ket{1} = \ket{0} 

Yゲート

Y\ket{0} = \color{red}{i}\ket{1} \ \ \ \ Y\ket{1} = \color{red}{-i}\ket{0} 

Zゲート

Z\ket{0} = \ket{0} \ \ \ \ Z\ket{1} = \color{red}{-1}\ket{1} 

X基底

X基底の計算は$\ket{0}と\ket{1}$にそれぞれ$X$ゲートを適用し求めます。
Z基底と同様に、ゲート適用で$\color{red}{1,-1,i,-i}$が現れます。

Xゲート

\displaylines{
X\ket{+} = \frac{X\ket{0}+X\ket{1}}{\sqrt{2}} = \frac{\ket{1}+\ket{0}}{\sqrt{2}} = \ket{+}
 \\
X\ket{-} = \frac{X\ket{0}-X\ket{1}}{\sqrt{2}} = \frac{\ket{1}-\ket{0}}{\sqrt{2}} = \color{red}{-1(}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\color{red}{)} = \color{red}{-1}\ket{-}
}

Yゲート

\displaylines{
Y\ket{+} = \frac{Y\ket{0}+Y\ket{1}}{\sqrt{2}} = \frac{i\ket{1}-i\ket{0}}{\sqrt{2}}=\color{red}{-i(}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\color{red}{)} = \color{red}{-i}\ket{-}
\\
Y\ket{-} = \frac{Y\ket{0}-Y\ket{1}}{\sqrt{2}} = \frac{i\ket{1}+i\ket{0}}{\sqrt{2}}=\color{red}{i(}\frac{\ket{0}+\ket{1}}{\sqrt{2}}\color{red}{)} = \color{red}{i}\ket{+}
}

Zゲート

\displaylines{
Z\ket{+} = \frac{Z\ket{0}+Z\ket{1}}{\sqrt{2}} = \frac{\ket{0}-\ket{1}}{\sqrt{2}} = \ket{-}
 \\
Z\ket{-} = \frac{Z\ket{0}-Z\ket{1}}{\sqrt{2}} = \frac{\ket{0}+\ket{1}}{\sqrt{2}} = \ket{+}
}

ここで、下記に着目頂きたいのですが、量子状態の観測は$\ket{0},\ket{1}$の相対的な関係が、観測結果に影響を与えます。一方で、ここで数式からくくりだされている$\color{red}{-1,-i,i}$は式全体に掛かっているため、$\ket{0}と\ket{1}$の相対的な関係に影響を及ぼしません。これがグローバル位相の正体です。
（と理解しています。）

\color{red}{-1(}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\color{red}{)} \ \ \ \ \ \ \
\color{red}{-i(}\frac{\ket{0}-\ket{1}}{\sqrt{2}}\color{red}{)} \ \ \ \ \ \ \ \ \ 
\color{red}{i(}\frac{\ket{0}+\ket{1}}{\sqrt{2}}\color{red}{)} 

Y基底

最後にY基底もやっておきましょう。要領はX基底と一緒です。
Z基底と同様に、ゲート適用で$\color{red}{1,-1,i,-i}$が現れます。

Xゲート

\displaylines{
X\ket{i} = \frac{X\ket{0}+iX\ket{1}}{\sqrt{2}} = \frac{\ket{1}+i\ket{0}}{\sqrt{2}} = \color{red}{i(}\frac{-i\ket{1}+\ket{0}}{\sqrt{2}} \color{red}{)} = \color{red}{i}\ket{i-}
 \\
X\ket{i-} = \frac{X\ket{0}-iX\ket{1}}{\sqrt{2}} = \frac{\ket{1}-i\ket{0}}{\sqrt{2}} = \color{red}{-i(}\frac{i\ket{1}+\ket{0}}{\sqrt{2}}\color{red}{)} = \color{red}{-i}\ket{i}
}

Yゲート

\displaylines{
Y\ket{i} = \frac{Y\ket{0}+iY\ket{1}}{\sqrt{2}} = \frac{i\ket{1}-i^{2}\ket{0}}{\sqrt{2}}=\frac{\ket{0}+i\ket{1}}{\sqrt{2}} = \ket{i}
\\
Y\ket{i-} = \frac{Y\ket{0}-iY\ket{1}}{\sqrt{2}} = \frac{i\ket{1}+i^{2}\ket{0}}{\sqrt{2}}=\color{red}{-1(}\frac{\ket{0}-i\ket{1}}{\sqrt{2}}\color{red}{)} = \color{red}{-1}\ket{i-} 
}

Zゲート

\displaylines{
Z\ket{i} = \frac{Z\ket{0}+iZ\ket{1}}{\sqrt{2}} = \frac{\ket{0}-i\ket{1}}{\sqrt{2}} = \ket{i-}
 \\
Z\ket{i-} = \frac{Z\ket{0}-iZ\ket{1}}{\sqrt{2}} = \frac{\ket{0}+i\ket{1}}{\sqrt{2}} = \ket{i}
}

まとめ

すべての計算結果をまとめると、下記となります。
特にX基底、Y基底については$\ket{+}\ket{-}\ket{i}\ket{i-}$が重ね合わせ状態なので、この重ね合わせ全体に係るグローバル位相としての$\color{red}{1,-1,i,-i}$が確認できます。

対象の基底	Xゲート適用 $X\ket{\psi}$	Yゲート適用 $Y\ket{\psi}$	Zゲート適用 $Z\ket{\psi}$
$\ket{0}$	$\ket{1}$	$\color{red}{i}\ket{1}$	$\ket{0}$
$\ket{1}$	$\ket{0}$	$\color{red}{-i}\ket{0}$	$\color{red}{-1}\ket{1}$
$\ket{+}=\frac{\ket{0}+\ket{1}}{\sqrt{2}}$	$\ket{+}$	$\color{red}{-i}\ket{-}$	$\ket{-}$
$\ket{-}=\frac{\ket{0}-\ket{1}}{\sqrt{2}}$	$\color{red}{-1}\ket{-}$	$\color{red}{i}\ket{+}$	$\ket{+}$
$\ket{i}=\frac{\ket{0}+i\ket{1}}{\sqrt{2}}$	$\color{red}{i}\ket{i-}$	$\ket{i}$	$\ket{i-}$
$\ket{i-}=\frac{\ket{0}-i\ket{1}}{\sqrt{2}}$	$\color{red}{-i}\ket{i}$	$\color{red}{-1}\ket{i-}$	$\ket{i}$

量子状態($\ket{\psi}$)の最終的な観測状態には影響を与えないが、状態としてはグローバル位相が存在するので、これを数式で表現できるように$\color{red}{e^{i\gamma}}$を付与しておくというのがグローバル位相の係数の意味なのだと思います。（と理解しています。）

\ket{\psi} = \color{red}{e^{i\gamma}} {\left(cos\dfrac{\theta}{2}\ket{0} +{e^{i\varphi}}sin\dfrac{\theta}{2}\ket{1} \right)}

補記すると

\begin{eqnarray}
\color{red}{e^{i\gamma}}=\left\{
  \begin{array}{ll}
    1 & (\gamma=0) \\
    i & (\gamma=\pi/2) \\ 
    -1 & (\gamma=\pi) \\
    -i & (\gamma=3\pi/2) 
  \end{array} \right.
\end{eqnarray}

\ \ \ \ \ \ 

\because \color{red}{e^{i\gamma}}  = cos\ \gamma + i\ sin\ \gamma

コメント等あれば頂ければ幸いです。

1. https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%AD%E3%83%83%E3%83%9B%E7%90%83 より引用 ↩