この記事について
- 基本の「キ」ですが、量子ゲートはなぜユニタリーでなければならないのか?
- 当たり前な内容なのですが、まとめて見たいと思います。
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
ユニタリー行列
こちらの記事でも触れましたが、量子ゲートはユニタリーです。
ユニタリー行列とは、下記を満たす複素正方行列Uのことで、実数行列での直交行列に対応します。
U^{\dagger}U = UU^{\dagger} = E
$U^{\dagger}$は、実数行列における転置行列に対応するのですが、複素行列を対象とする場合には、複素数に対して複素共役とった複素転置(エルミート共役)の行列を指します。
例えば、$pauli$-$XZY$は下記の通りユニタリーです。
\displaylines{
XX^{\dagger} =
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
=E
\\
ZZ^{\dagger} =
\begin{bmatrix}
1 & 0 \\
0 & -1
\end{bmatrix}
\begin{bmatrix}
1 & 0 \\
0 & -1
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
=E
\\
YY^{\dagger} =
\begin{bmatrix}
0 & -i \\
i & 0
\end{bmatrix}
\begin{bmatrix}
0 & -i \\
i & 0
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
=E
}
ゲート演算は時間発展
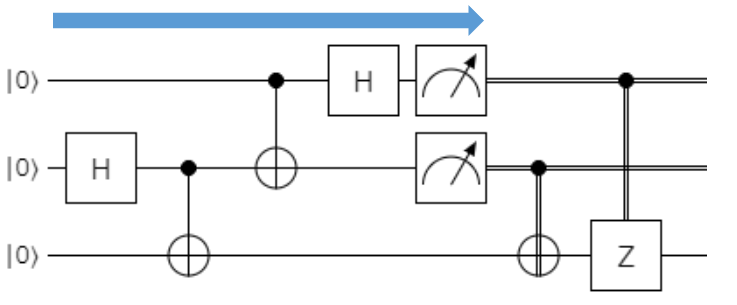
量子ゲートでの演算は、状態ベクトル($\ket{\psi}$)に対して順次量子ゲートを適用する行為は、状態ベクトルに対する時間発展を表現しており、ゲートの左から右へと順次時間が進行します。
\ket{\psi} = \alpha\ket{0} + \beta\ket{1}\ \ \ \ \alpha ,\beta \in \mathbb{C_{複素数}}
確率振幅($\alpha$,$\beta$)は、どのタイミングにおいても下記の規格化条件を満たすのが、演算のルールですので、どの時刻においても下記関係式を満たす必要があります。
|\alpha|^2 + |\beta|^2 = 1
規格化条件の確認方法
ある状態ベクトル($\ket{\psi}$)が規格化条件を満たしているか?は簡単に計算ができます。
具体的には、
\ket{\psi} = \alpha\ket{0} + \beta\ket{1} \ \ \ \ \leftrightarrow \ \ \ \ \ \ket{\psi} = \tate{\alpha}{\beta}
ですので、下記を計算し1であれば、確率振幅($\alpha$,$\beta$)は規格化条件を満たします。
なお、$\alpha,\beta$は複素数なので、転置で複素共役をとります。
\bracket{\psi}{\psi} = \yoko{\alpha^{*}}{\beta^{*}}\tate{\alpha}{\beta} = 1
ゲート適用と確率振幅
時刻$t$における状態ベクトル($\ket{\psi_{t}}$)に対し、任意のゲート($U$)を適用し、状態が
\ket{\psi_{t}} \rightarrow \ket{\psi_{t+1}}
と変化しました。
状態変化後の$\ket{\psi_{t+1}}$において、規格化条件を満たしているかを確認してみたいと思います
\ket{\psi_{t+1}} = U\ket{\psi_{t}} = U(\alpha\ket{0} + \beta\ket{1})
\ \ \ \
\leftrightarrow
\ \ \ \
\ket{\psi_{t+1}} = U\ket{\psi_t} = U\tate{\alpha}{\beta}
ですので、先程と同様に$\ket{\psi_{t+1}}$の、$bra$-$ket$を計算します。
$\ket{\psi_{t+1}}$は上記の通り$\ket{\psi_{t}}$にゲート$U$が適用された状態ですので
\bracket{\psi_{t+1}}{\psi_{t+1}} =
(\yoko{\alpha^{*}}{\beta^{*}}U^{\dagger})(U\tate{\alpha}{\beta})
となります。
$U$は実数空間ではなく、複素空間を想定していますので、$ket \rightarrow bra$の際に、複素転置(エルミート共役)をとるので、$U \rightarrow U^{\dagger}$となります。
規格化条件は、
\bracket{\psi_{t+1}}{\psi_{t+1}} = 1
でしたので、
(\yoko{\alpha^{*}}{\beta^{*}}U^{\dagger})(U\tate{\alpha}{\beta}) = 1 \tag{*1}
であるかを検討します。
ゲートにより状態が変化する前は、$\alpha,\beta$は規格化条件を満たしていたはずですので、
\bracket{\psi}{\psi} = \yoko{\alpha^{*}}{\beta^{*}}\tate{\alpha}{\beta} = 1
が成り立つはずです。
これを前提とすると$(*1)$が成立するための条件とは、何でしょうか。
そうです。
U^{\dagger}U = E
を満たす必要があります。そして上記を満たす複素正方行列$U$こそがユニタリー行列となります。
まとめ
量子ゲート回路は、時間発展による $\ket{\psi}$の状態変化を表現しています。
そしてどの時刻断面においても規格化条件を満たそうとすると、$\ket{\psi}$に適用される量子ゲートはどうしても、ユニタリーでなくてはならない。
これが量子ゲートがユニタリーな理由となります。
コメント等あれば頂ければ幸いです。