※こちらはPythonデータ分析勉強会#04の発表資料です。
ディープラーニングを使った画像の異常検知は、GANを使った手法やAutoEncoderを使った手法など多くあります。以前に、Variational Autoencoderを使った画像の異常検知という記事も書きました。
今回紹介する手法は、通常の畳み込みニューラルネットワーク(CNN)を使って、損失関数を工夫することにより、異常検知する手法です。
「Learning Deep Features for One-Class Classification」(以下、DOC)
https://arxiv.org/abs/1801.05365
結果からいうと、本手法は異常検知精度が良くて、異常個所の可視化も可能であることが分かりました。
概要
この論文は、発表当時にstate-of-the-artを達成したとのことです。
早速実装したいところですが、まずは概要をご説明します。
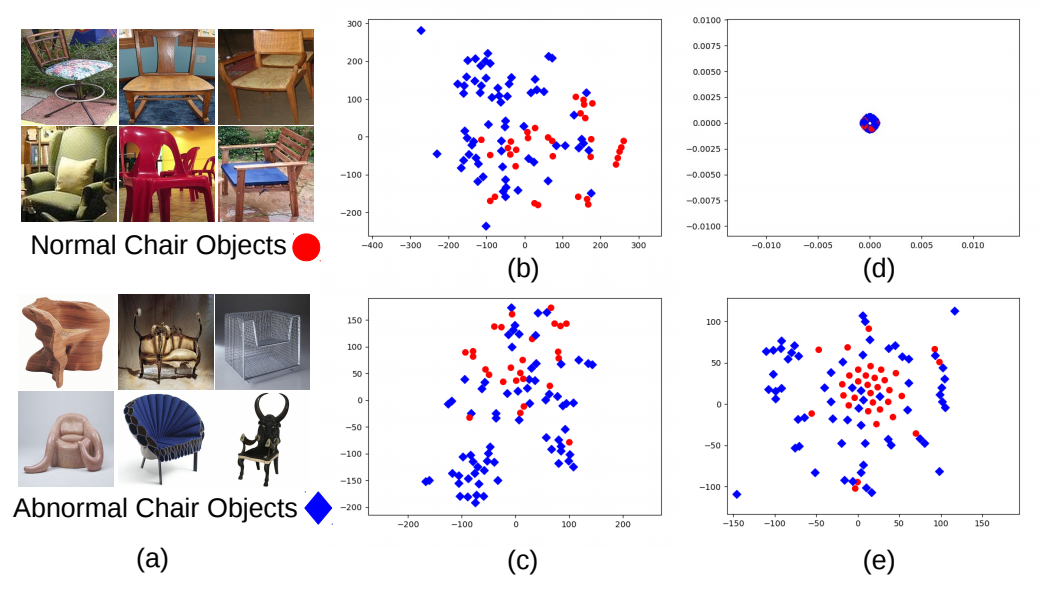
下の図は、通常のCNNを使って色々な条件で学習させ、畳み込み層からの
出力をt-SNEで可視化したものです。
- 図(b):Alexnetの学習済モデルでNormal と Abnormal を分布させた図
- 図(c):Normal vs Abnormalで学習させた図
- 図(e):提案手法(DOC)
図(b)でも異常検知できるじゃん!と思ったのは、私だけじゃないはず。
ただ、図(e)と比べると何となく見劣りします。
論文では、最終的に(e)でk近傍法を使い、異常検知させています。
学習のさせ方は、異常検知させたい画像を見ながら、全く別の種類の画像を見て、異常検知させたい画像の範囲を絞っていくようなイメージになります。
データの準備
学習は以下のデータを用意します。
| 名称 | 中身 | 具体例 | クラス数 |
|---|---|---|---|
| ターゲットデータ | 異常検知させたい画像 | 工業製品など | 1 |
| リファレンスデータ | 上記と関係ないデータセット | ImageNetやCIFAR-10 | 10とか1,000 |
モデルの準備
- ディープラーニングのモデル(g)は学習済モデルを準備する。
- 論文では、gはAlexnetやVGG16を使っている。hはImageNetなら1000個のノード、CIFAR-10なら10個のノードになる。
- 学習中、Reference Network(R)とSecondary Network(S)のgとhは共有させている。
- また学習中、最後から4つの層以外は重みを固定している。
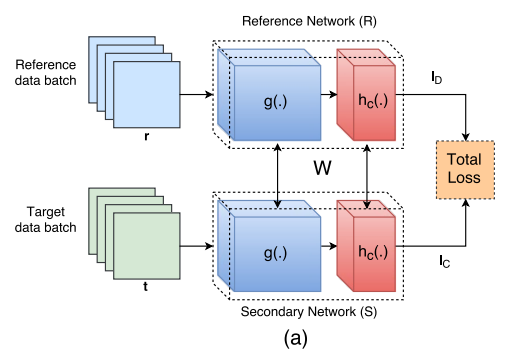
学習フェーズ
- まず、リファレンスデータを使って、Rで**損失関数$l_D$**を計算させる。
- 次に、ターゲットデータを使って、Sで**損失関数$l_C$**を計算させる。
- 最後に、$l_D$と$l_C$でRとSを同時に学習させる。
Total Loss$L$は以下の式で定義されます。
L=l_D+\lambda l_C
$l_D$は、通常の分類問題で使われるクロスエントロピーを使っています。
また、論文では$\lambda=0.1$としています。
一番重要なコンパクトロス$l_C$は次のように算出されます。
バッチサイズをnとし、gからの出力(k次元)を$x_i\in R^k$とする。そして$z_i$を以下のように定義します。
z_i = x_i - m_i\\
m_i = \frac{1}{n-1}\sum_{j\not=i}x_j
$m_i$は、バッチ内における$x_i$以外の出力の平均値です。このとき、$l_C$は以下のように定義されます。
l_{C}=\frac{1}{nk}\sum_{i=1}^nz_i^Tz_i
イメージとして、(厳密には違いますが)$l_C$はバッチ内の出力の分散と見てよいでしょう。
$l_C$のコードを組む際は、「$x_i$以外の平均値」の処理を書くのが面倒くさいので、
論文の付録に書いてある以下の式を使いました。
l_{C}=\frac{1}{nk}\sum_{i=1}^n\frac{n^2\sigma^2_i}{(n-1)^2}\\
\sigma^2_i=[x_i-m]^T[x_i-m]
ただし、$m$はバッチ内の出力の平均値です。
そして、学習時にはクロスエントロピー$l_D$と共に、出力の分散である$l_C$も小さくなるように学習させます。
なお、learning rateは$5\times10^{-5}$、weight decayは0.00005としているようです。
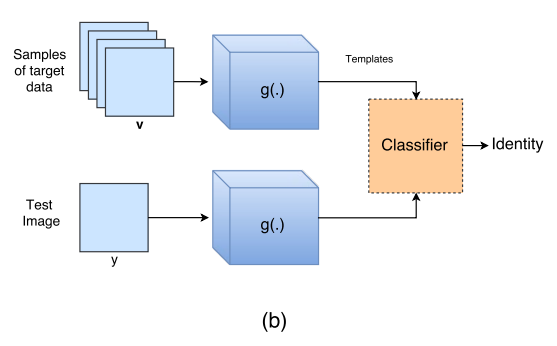
テストフェーズ
- モデルからhを取り除く。
- まず、ターゲットデータの学習データから画像を持ち込み、gに入れ分布を取得する。
- 次にテストさせたい画像をgに入れ、分布を取得する。
- 最後に、「学習データの画像の分布」と「テストの画像の分布」でk近傍法を使って異常検知させる。
Kerasによる実装
学習済モデルは、軽いMobileNetV2を使います。
将来的に、ラズパイで実装したいからです。
データのロード
今回使用するデータは、以前と同様にFashion-MNISTを使います。
そして、以下のようにデータを振り分けました。
| 個数 | クラス数 | 備考 | |
|---|---|---|---|
| リファレンスデータ | 6,000 | 8 | スニーカーとブーツを除く |
| ターゲットデータ | 6,000 | 1 | スニーカー |
| テストデータ(正常) | 1,000 | 1 | スニーカー |
| テストデータ(異常) | 1,000 | 1 | ブーツ |
from keras.datasets import fashion_mnist
from keras.utils import to_categorical
import numpy as np
import matplotlib.pyplot as plt
# dataset
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
x_train = x_train.astype('float32') / 255
x_test = x_test.astype('float32') / 255
# 学習データ
x_train_s, x_test_s, x_test_b = [], [], []
x_ref, y_ref = [], []
x_train_shape = x_train.shape
for i in range(len(x_train)):
if y_train[i] == 7:#スニーカーは7
temp = x_train[i]
x_train_s.append(temp.reshape((x_train_shape[1:])))
else:
temp = x_train[i]
x_ref.append(temp.reshape((x_train_shape[1:])))
y_ref.append(y_train[i])
x_ref = np.array(x_ref)
# refデータからランダムに6000個抽出
number = np.random.choice(np.arange(0,x_ref.shape[0]),6000,replace=False)
x, y = [], []
x_ref_shape = x_ref.shape
for i in number:
temp = x_ref[i]
x.append(temp.reshape((x_ref_shape[1:])))
y.append(y_ref[i])
x_train_s = np.array(x_train_s)
x_ref = np.array(x)
y_ref = to_categorical(y)
# テストデータ
for i in range(len(x_test)):
if y_test[i] == 7:#スニーカーは7
temp = x_test[i,:,:,:]
x_test_s.append(temp.reshape((x_train_shape[1:])))
if y_test[i] == 9:#ブーツは9
temp = x_test[i,:,:,:]
x_test_b.append(temp.reshape((x_train_shape[1:])))
x_test_s = np.array(x_test_s)
x_test_b = np.array(x_test_b)
データのリサイズ
MobileNetv2では、最小入力サイズが$(96\times96\times3)$となっています。
そのため、Fashion-MNIST$(28\times28\times1)$をそのまま使うことはできません。
そこで、データをリサイズします。
import cv2
from PIL import Image
def resize(x):
x_out = []
for i in range(len(x)):
img = cv2.cvtColor(x[i], cv2.COLOR_GRAY2RGB)
img = cv2.resize(img,dsize=(96,96))
x_out.append(img)
return np.array(x_out)
X_train_s = resize(x_train_s)
X_ref = resize(x_ref)
X_test_s = resize(x_test_s)
X_test_b = resize(x_test_b)
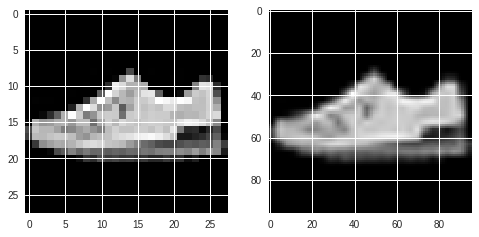
図にすると以下のようになります。
左図が元データ$(28\times28\times1)$、右図がリサイズ後$(96\times96\times3)$。
モデルの構築と学習
モデルの構築と学習のコードは長いので、付録に載せておきます。
学習中は、畳込み層の後半は重みを固定しています。
ここでは、コードの一部を解説します。
Kerasを使えば、モデルの構築などは簡単でしたが、以下の損失関数が闇でした。
def original_loss(y_true, y_pred):
lc = 1/(classes*batchsize) * batchsize**2 * K.sum((y_pred -K.mean(y_pred,axis=0))**2,axis=[1]) / ((batchsize-1)**2)
return lc
Kerasで損失関数を自作している人は少なく、情報が全然出てきませんでした。
間違っているところがありましたら、ご連絡ください。
また、気を付けていただきたいのが、この部分。
# target data
# 学習しながら、損失を取得
lc.append(model_t.train_on_batch(batch_target, np.zeros((batchsize, feature_out))))
# reference data
# 学習しながら、損失を取得
ld.append(model_r.train_on_batch(batch_ref, batch_y))
model_t.train_on_batchでは、教師データは何でも良いので、ダミーでゼロ行列
np.zeros((batchsize, feature_out))を与えています。
さらに、Kerasで$l_D$と$l_C$を同時に学習させる手段が思いつかず、$l_C$で学習させてから
$l_D$を学習させるという、強引なやり方をしております。
損失関数や同時学習はPytorchであれば、すんなりいくのかなぁと思っており、
最近Pytorchへの引っ越しを考えています。
結果
分布を眺める
異常検知の性能を見る前に、t-sneで分布を可視化します。
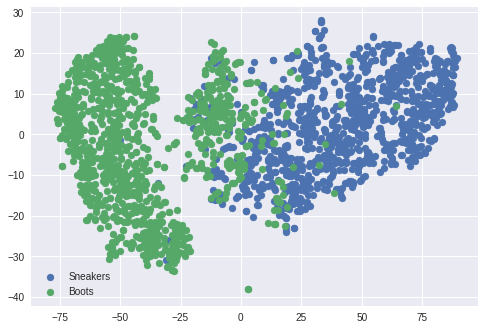
下の図は、テストデータの画像($96\times96\times3$)をそのまま可視化したものです。
入力データそのままでも、スニーカーとブーツは結構分離しています。
しかし、一部は混在しているようです。
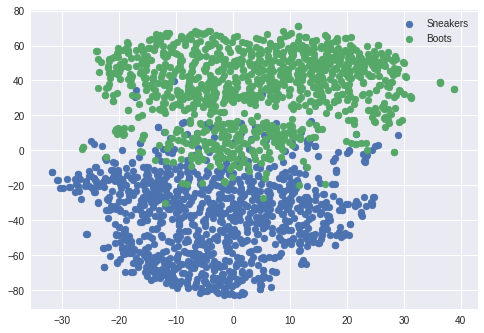
続いて、下の図はDOCで学習したCNN(MobileNetV2)を使って、テストデータの
出力(1280次元)をt-sneで可視化したものです。
先ほどの図と同様にうまく分離出来ています。ここで強調したいのは
CNNはスニーカー(正常品)の画像しか学習していないという点です。
それにもかかわらず、スニーカーとブーツがうまく分離されているという
のは、驚くべきことです。正に異常検知です。
これはDOCによる転移学習のおかげといえ、CNNが画像の見るべきポイントをあらかじめ
学習してあったので、うまくいったといえます。
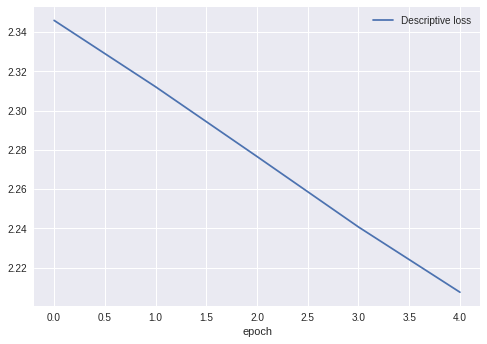
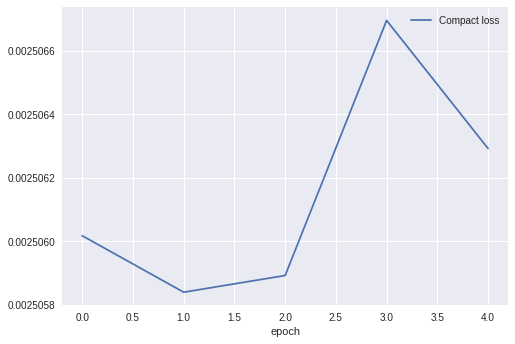
一応、学習中の損失関数の推移も掲載しておきます。
異常検知性能
次にgの出力で異常検知させます。論文ではk近傍法を使っていましたが、
実装ではLOFを使います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
from sklearn import metrics
from sklearn.preprocessing import MinMaxScaler
train = model.predict(X_train_s)
test_s = model.predict(X_test_s)
test_b = model.predict(X_test_b)
train = train.reshape((len(X_train_s),-1))
test_s = test_s.reshape((len(X_test_s),-1))
test_b = test_b.reshape((len(X_test_b),-1))
# 0-1に変換
ms = MinMaxScaler()
train = ms.fit_transform(train)
test_s = ms.transform(test_s)
test_b = ms.transform(test_b)
# fit the model
clf = LocalOutlierFactor(n_neighbors=5)
y_pred = clf.fit(train)
# 異常スコア
Z1 = -clf._decision_function(test_s)
Z2 = -clf._decision_function(test_b)
# ROC曲線の描画
y_true = np.zeros(len(test_s)+len(test_b))
y_true[len(test_s):] = 1#0:正常、1:異常
# FPR, TPR(, しきい値) を算出
fpr, tpr, _ = metrics.roc_curve(y_true, np.hstack((Z1, Z2)))
# AUC
auc = metrics.auc(fpr, tpr)
# ROC曲線をプロット
plt.plot(fpr, tpr, label='DeepOneClassification(AUC = %.2f)'%auc)
plt.legend()
plt.title('ROC curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.grid(True)
plt.show()
ROC曲線は以下のとおりです。
AUCは驚愕の0.90!以前記事にしたVAEを大きく上回っています。
ちなみに、**全体の精度は83%**くらい出ています。
以前の結果と比べると、以下のとおりです。
| 性能(AUC) | 判定速度(msec/1枚) | 可視化 | |
|---|---|---|---|
| VAE(小窓) | 0.58 | 0.80 | × |
| VAE+非正則化(小窓) | 0.67 | 4.3 | 〇 |
| DOC(MobileNetV2) | 0.90 | 140 | △ |
※判定速度はColaboratoryのGPUで計測しています。
※DOCの可視化は次節で説明します。
DOCは性能で圧勝だったものの、判定速度ではLOFを使っているせいか遅いです。
DOCを高速化する方法は、次回の記事で書きます。約10倍速くなります。
ちなみにDOC+VGG16だと370msec/1枚になりました。
やはり、MobileNetV2は速いですね。
また、精度で劣った「VAE+非正則化」は、ねじ山のような複雑な画像のために
考案されたものです。そのため、複雑な画像だと、性能はVAE+非正則化>DOCとなる
かもしれません。
画像と異常スコアの関係
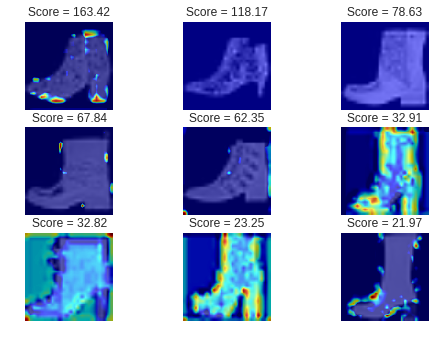
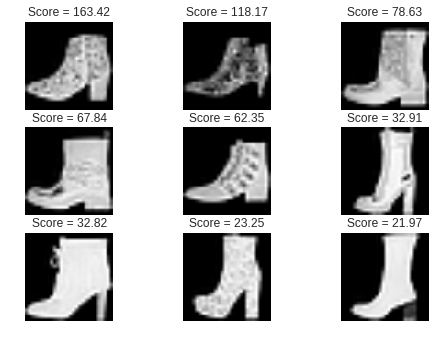
次に、ブーツ(異常品)の画像と異常スコアの関係を見てみましょう。
異常スコアは大きければ大きいほど、スニーカー(正常品)から外れていると見なします。
まずは、異常スコアが大きかった画像、つまりスニーカーに全然似ていないと
判定されたブーツの画像です。
確かに、スニーカーに全然似ていません。
次に、異常スコアが小さかった画像、つまりスニーカーに酷似していると
判定されたブーツの画像です。
全体的にハイカットのスニーカーに似ています。
これは人間がやっても誤判定してしまうかもしれません。
直感的に、DOCによる異常スコアは大きいほど、正常品から乖離していると
いえるかもしれません。
Kerasによる可視化
論文には出てきませんが、Grad-CAMによる可視化もやってみました。
工業製品で使うことを考えると、どこに異常があるのか可視化するのも重要です。
Grad-CAM
Grad-CAMはCNNの分類問題でよく使われます。分類問題で使うと、その分類の
根拠となった箇所を示してくれます。詳しくは、以下の記事をご覧ください。
https://qiita.com/bele_m/items/a7bb15313e2a52d68865
https://qiita.com/haru1977/items/45269d790a0ad62604b3
今回は、DOCでGrad-CAMをそのまま使ってみました。
結果
まずは、異常スコアが大きかったブーツの画像で、Grad-CAMを使ってみました。
うまくいったところでは、かかと部分やブーツの垂直部分が赤くなっており、
スニーカーと全然似ていない部分が可視化されています。
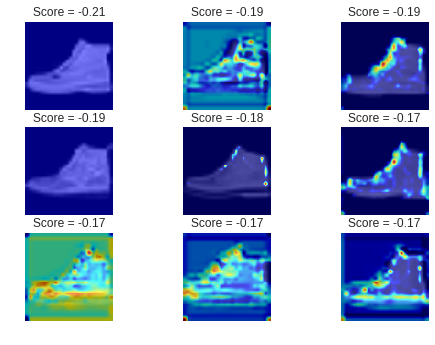
次に、異常スコアが小さいブーツの画像でGrad-CAMを使ってみます。
うまくいったところでは、ハイカット部分が赤くなっており、スニーカーと
似ていない部分が可視化されています。
全体的に、可視化が成功するかどうかは五分五分といった感じで、
全結合層を追加するなど、改良の余地がありそうです。
それよりも問題なのは、処理時間が5秒/画像1枚(Colaboratory-GPU)
ほどかかり、とてもリアルタイムでは使えないという点です。使うシーンを
考えないと全く使えない機能になりそうです。
なお、Grad-CAMのコードは、前述したリンクからコピペだったので省略します。
まとめ
DOCを使ってみた感想は、以下のとおりです。
- DOCは、以前投稿したVAEよりも性能が良い
- 異常個所の可視化は、ある程度可能であるが、処理時間が長い
- 理論は、難解ではなく理解しやすい
- 「精度」と「速度」を天秤にかけて、学習済モデルを自由に変えられるため、非常に柔軟性がある手法
次回はラズパイで実装します。
どのくらいサクサク動くのか楽しみです。
2019/3/7追記 可視化部分を改良しました。
https://qiita.com/shinmura0/items/c2f7a86b156ebc5c5daa
2019/5/16追記 弱異常検知(AUC:0.99)の記事を書きました。
https://qiita.com/shinmura0/items/1af83f5a5857d50cabc2
付録
最後に、モデル構築と学習のコードを掲載します。
1/9 コード修正
from keras.applications import MobileNetV2, VGG16
from keras.optimizers import SGD
from keras.models import Model
from keras.layers import GlobalAveragePooling2D, Dense
from keras import backend as K
from keras.engine.network import Network
input_shape = (96, 96, 3)
classes = 10
batchsize = 128
# feature_out = 512 #secondary network out for VGG16
feature_out = 1280 #secondary network out for MobileNet
alpha = 0.5 #for MobileNetV2
lambda_ = 0.1 #for compact loss
# 損失関数
def original_loss(y_true, y_pred):
lc = 1/(classes*batchsize) * batchsize**2 * K.sum((y_pred -K.mean(y_pred,axis=0))**2,axis=[1]) / ((batchsize-1)**2)
return lc
# 学習
def train(x_target, x_ref, y_ref, epoch_num):
# VGG16読み込み, S network用
print("Model build...")
#mobile = VGG16(include_top=False, input_shape=input_shape, weights='imagenet')
# mobile net読み込み, S network用
mobile = MobileNetV2(include_top=True, input_shape=input_shape, alpha=alpha,
, weights='imagenet')
#最終層削除
mobile.layers.pop()
# 重みを固定
for layer in mobile.layers:
if layer.name == "block_13_expand": # "block5_conv1": for VGG16
break
else:
layer.trainable = False
model_t = Model(inputs=mobile.input,outputs=mobile.layers[-1].output)
# R network用 Sと重み共有
model_r = Network(inputs=model_t.input,
outputs=model_t.output,
name="shared_layer")
#Rに全結合層を付ける
prediction = Dense(classes, activation='softmax')(model_t.output)
model_r = Model(inputs=model_r.input,outputs=prediction)
#コンパイル
optimizer = SGD(lr=5e-5, decay=0.00005)
model_r.compile(optimizer=optimizer, loss="categorical_crossentropy")
model_t.compile(optimizer=optimizer, loss=original_loss)
model_t.summary()
model_r.summary()
print("x_target is",x_target.shape[0],'samples')
print("x_ref is",x_ref.shape[0],'samples')
ref_samples = np.arange(x_ref.shape[0])
loss, loss_c = [], []
print("training...")
#学習
for epochnumber in range(epoch_num):
x_r, y_r, lc, ld = [], [], [], []
#ターゲットデータシャッフル
np.random.shuffle(x_target)
#リファレンスデータシャッフル
np.random.shuffle(ref_samples)
for i in range(len(x_target)):
x_r.append(x_ref[ref_samples[i]])
y_r.append(y_ref[ref_samples[i]])
x_r = np.array(x_r)
y_r = np.array(y_r)
for i in range(int(len(x_target) / batchsize)):
#batchsize分のデータロード
batch_target = x_target[i*batchsize:i*batchsize+batchsize]
batch_ref = x_r[i*batchsize:i*batchsize+batchsize]
batch_y = y_r[i*batchsize:i*batchsize+batchsize]
#target data
#学習しながら、損失を取得
lc.append(model_t.train_on_batch(batch_target, np.zeros((batchsize, feature_out))))
#reference data
#学習しながら、損失を取得
ld.append(model_r.train_on_batch(batch_ref, batch_y))
loss.append(np.mean(ld))
loss_c.append(np.mean(lc))
if (epochnumber+1) % 5 == 0:
print("epoch:",epochnumber+1)
print("Descriptive loss:", loss[-1])
print("Compact loss", loss_c[-1])
#結果グラフ
plt.plot(loss,label="Descriptive loss")
plt.xlabel("epoch")
plt.legend()
plt.show()
plt.plot(loss_c,label="Compact loss")
plt.xlabel("epoch")
plt.legend()
plt.show()
return model_t
model = train(X_train_s, X_ref, y_ref, 5)