ディープラーニングを使った「画像の異常検知」が流行りつつあります。
通常の異常検知は正常画像のみで学習させます(例えばこちら)。
今回は、運よく少量の異常画像を手に入れたとして、異常画像と正常画像を
組み合わせて異常検知性能を上げる方法を考えてみます。
※こちらはPythonデータ分析勉強会#08の発表資料です。
結論から
結論からいうと、少量の異常画像とmetric learningを使えば、異常検知性能を上げることが可能です。
精度でいうと、10%弱向上するかもしれません。
| AUC | |
|---|---|
| 異常検知 | 0.94 |
| 弱異常検知 | 0.97 |
※本稿では、「正常画像」と「少量の異常画像」を組み合わせて異常検知する手法を
弱異常検知と呼んでいます。論文のサーベイは全くしておらず、もし、他の呼び方が
あれば、教えていただけるとありがたいです。
想定するシーン
製造ラインの画像による異常検知を想定します。
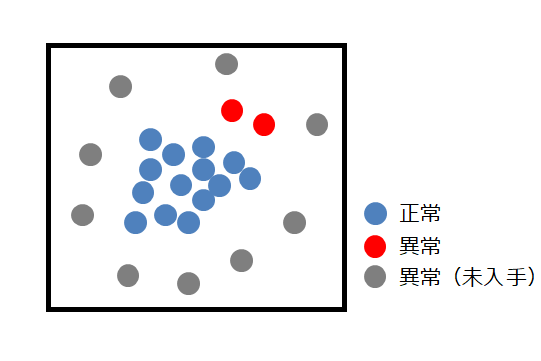
以下のように、データが手元にあったとします。
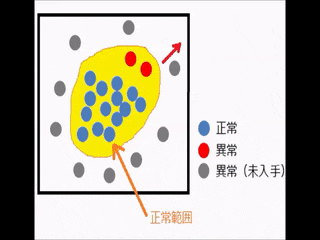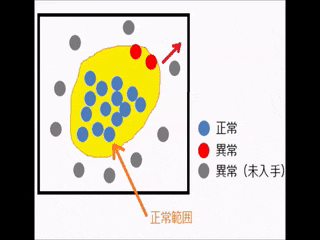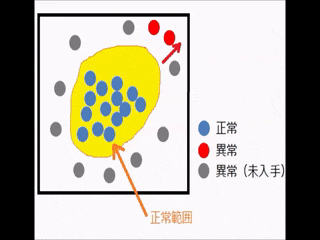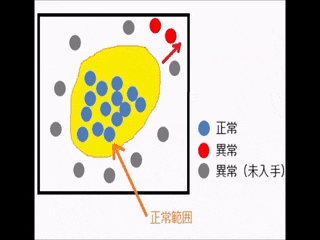
青と赤は手元にある画像です。
グレーは異常な画像ですが、手元にない(未入手の画像)です。
異常な状態はほとんど発生しないので、あらゆる異常画像(全てのグレーの
画像)を入手するのは困難と仮定します。
考え方
教師あり学習と異常検知
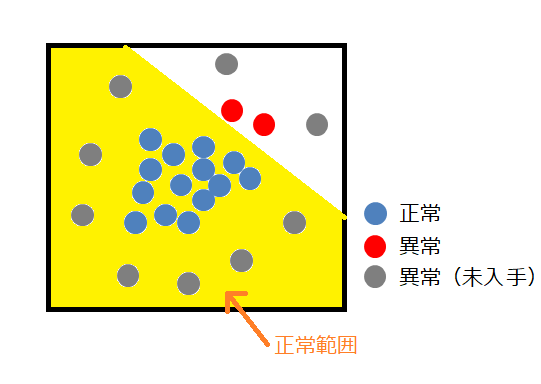
このまま手元にある画像(赤と青)で「教師あり学習」をすると、以下のように
正常範囲が広くなる可能性があります。
ご覧のように、グレーの画像(異常画像)も正常範囲に入ってしまいました。
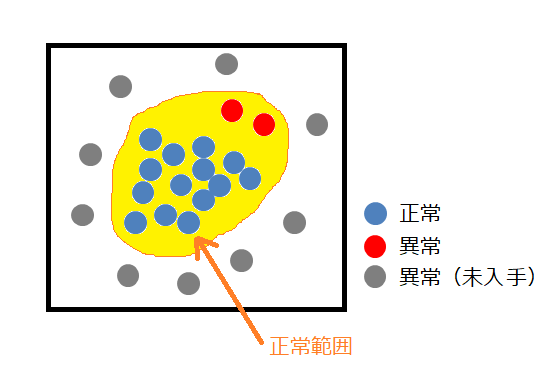
そこで、登場するのが異常検知です。正常画像のみ(青の画像)で学習させる
ことにより、正常範囲をある程度絞ることが可能です。
さきほどの図と比べると、正常範囲が狭くなったため、異常検知性能が上がりました。
ところが、今度は赤の画像(異常画像)が正常範囲に入ってしまいました。
赤の画像は学習に使用していないため、正常範囲に入ってしまう可能性があります。
折角、赤の画像(異常画像)が手元にあるので、これを活用できないか?、つまり
異常だと覚えこませることはできないか?と考えます。
正常画像と異常画像でmetric learning
ここで登場するのが、metric learningです。詳細な説明は他の記事に譲りますが
(例えばこちら)、同じラベルの画像を固めてプロットしてくれる効果があります。
metric learning単体でも異常検知は可能で、その異常検知性能は高く現場で使えます。
つまり、正常画像で学習させると、先ほどの図のようにすることが可能です。
もう一つ、metric learningの特長として、異なるラベルの画像は遠くにプロットして
くれる効果もあります(こちらを参照)。
ここで、勘の良い方なら気付くかもしれません。
「正常画像」と「手持ちの異常画像」をmetric learningで学習させることにより、
正常画像と手持ちの異常画像を離してプロットできるのではないか?
これによって、異常検知性能が向上するのではないか?というのが本稿のテーマです。
弱異常検知の学習手順
-
ステップ1 データの準備
用意するデータは「正常画像」と少量(多くても良い)の「異常画像」、
そしてcifar-10などの「ラベル付きの画像」です。 -
ステップ2 metric learningで教師あり学習
各画像にラベルを付与し、教師あり学習を実行します。
ただし、学習のさせ方はmetric learningとします。 -
ステップ3 全結合層の削除
学習完了後、クラス分類用の全結合層が付いている場合は、削除します。 -
ステップ4 正常画像で分布を取得
ステップ3で作ったCNNに、教師あり学習で使用した正常画像を入力し、分布を取得します。
そして、正常範囲を見積ります。(厳密にいうと正常範囲は後で決めます。) -
ステップ5 異常検知の実行
テスト画像で異常スコアを算出します。本稿では、K近傍法(LOF)だけでなく、
ユークリッド距離、マハラノビス距離も使って異常スコアを算出します。
ステップ2 metric learningで教師あり学習
metric learningにも種類がありますが、今回はL2 softmax lossを使います。
実装はとても簡単で、クラス分類用の全結合層の前に一層加えるだけで良いです。
Kerasで書くと以下の通りです。
c = GlobalAveragePooling2D()(c)
c = keras.layers.Lambda(lambda xx: alpha*(xx)/K.sqrt(K.sum(xx**2)))(c) #metric learning
c = Dense(classes, activation='softmax')(c)
ただし、$\alpha$はパラメーターです。
ステップ3 全結合層の削除
ここはDOCと考え方は同じです。
具体的には最終層を削除してモデルを再構築します。
# 最終層削除
model.layers.pop()
model = Model(inputs=model.input,outputs=model.layers[-1].output)
ステップ5 異常検知の実行
異常スコアの出し方は、DOCではLOFを使いましたが、これがベストでもないようです。
その他には、ユークリッド距離やマハラノビス距離が考えられます。
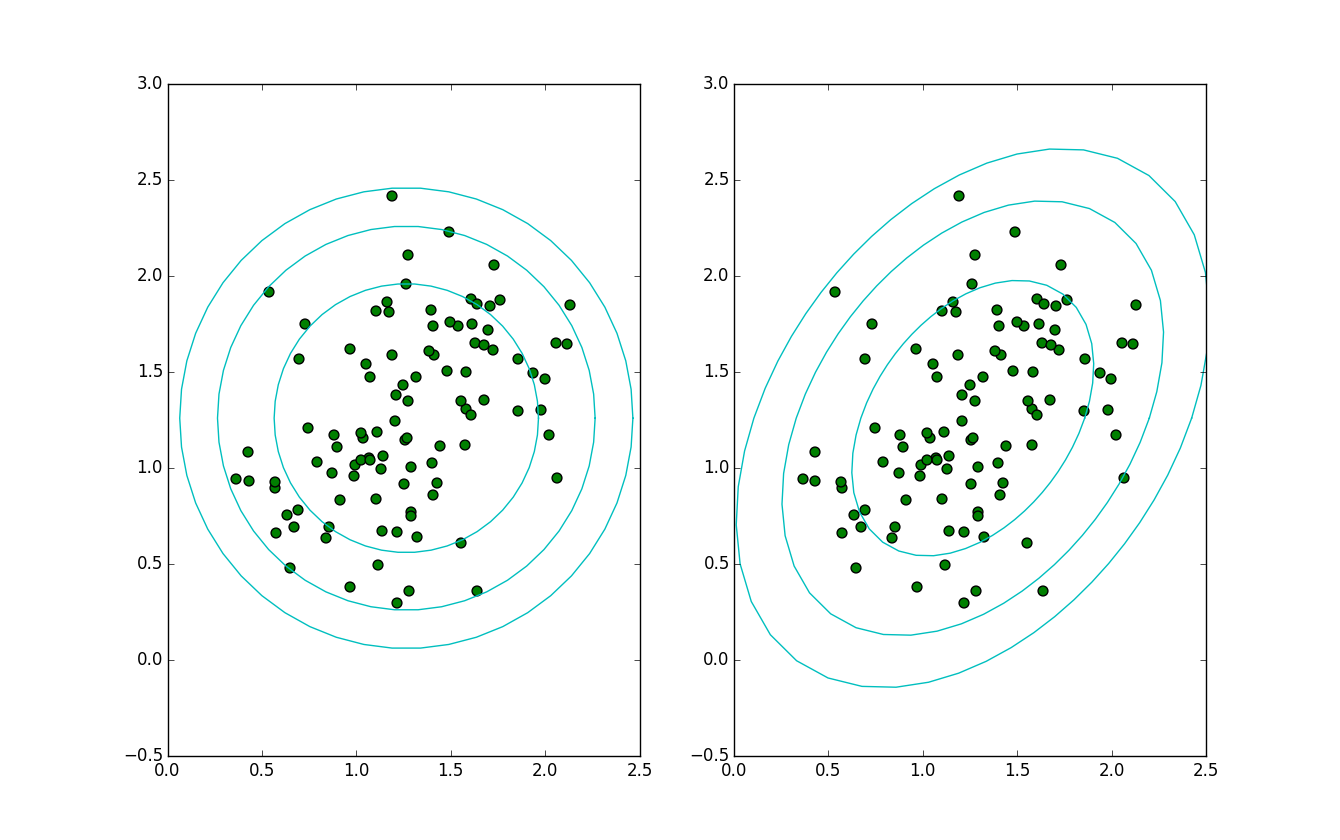
2次元の図で表すと以下のようになります。
左側はユークリッド距離です。一般的な距離です。
右側はマハラノビス距離です。こちらは相関を考慮した距離になります。
実験
Fashion MNIST
学習のコードはgithubに置きました。
条件設定
DOCと同様にスニーカー(正常)とブーツ(異常)を題材に実験します。
| 枚数 | クラス数 | 備考 | |
|---|---|---|---|
| 学習データ | 4,500 | 8 | スニーカーとブーツを除く |
| 学習データ(正常) | 500 | 1 | スニーカー |
| 学習データ(異常) | 10 | 1 | ブーツ(弱異常検知で使用) |
弱異常検知で使う異常画像は、正常画像に対し**2%(10枚)**の割合になっています。
こんなわずかな異常画像で効果があるのか?と思いますが、とりあえず実験してみましょう。
テストデータの内訳は以下のとおりです。
| 枚数 | クラス数 | 備考 | |
|---|---|---|---|
| テストデータ(正常) | 1,000 | 1 | スニーカー |
| テストデータ(異常) | 1,000 | 1 | ブーツ |
その他の条件は以下のとおりです。
- CNNのモデルはMobilNetV2を使う。
- 異常スコアの算出はLOFを使う。
- 実験は10回行い、データの中身は同一とする。
- 弱異常検知では、学習データ(異常)10枚を水増しして500枚にする。
結果
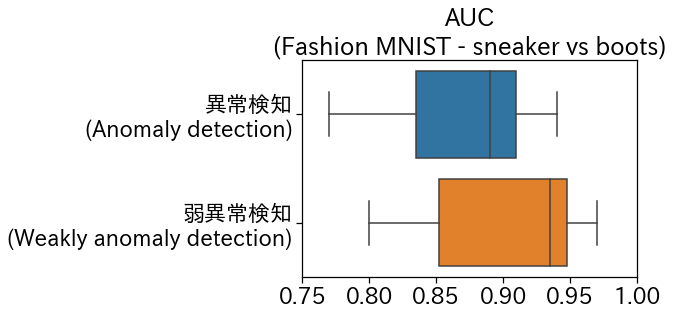
AUCの結果は以下のとおりです。
結果はご覧のとおり、弱異常検知の方が良い結果となりました。
ベストな結果を比較してみます。
||AUC|
|---|---|---|
|異常検知|0.94|
|弱異常検知|0.97|
|DOC(参考)|0.90|
弱異常検知は、異常検知に対しAUCが3ポイント上昇しています。
これは、正常画像500枚に対し、わずか2%の異常画像を入れるだけで精度が改善するということです。
異常画像が入手可能であれば、弱異常検知をやる価値はあると思います。
自前の画像
自分にとっては、こちらの実験の方が主題でした。
ディープラーニングを使ったインターフェイスの開発を進めており、手の形で異常検知させています。
Fashion MNISTとの違いは以下のとおりです。
- 手元にある画像が少ない
- cifar-10と一緒に学習させる
- 転移学習は使わない(自作モデル)
条件設定
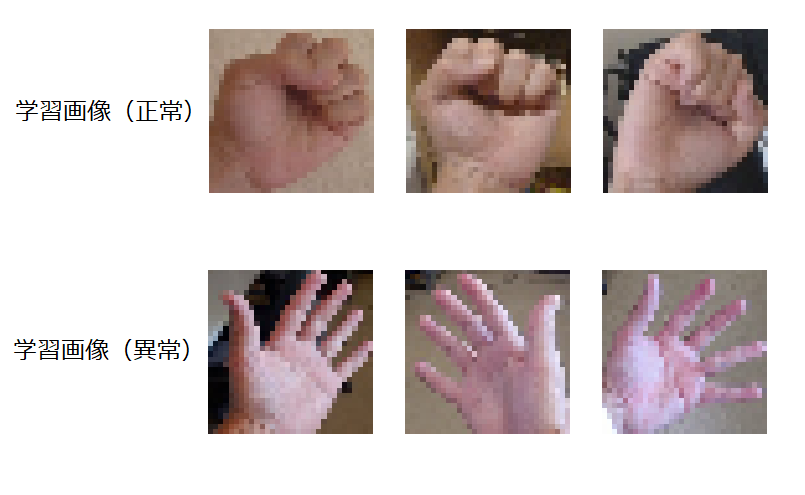
今回用意したのは、自分の手の画像です。
| 枚数 | |
|---|---|
| 学習データ(正常) | 21 |
| 学習データ(異常) | 30 |
正常画像がとても少ないです。ここでやりたいことは「グー」と「それ以外」の形を
見分けたくて学習させています。ただ、学習用の異常画像は「パー」の形しか集めていません。
しかし、テスト用の異常画像は「パー」以外も含まれます。
| 枚数 | |
|---|---|
| テストデータ(正常) | 15 |
| テストデータ(異常) | 21 |
実際に学習させるときは、PCACAで学習データのコントラストを
変えながらDataAugmentationして、それぞれ5000枚に増幅しています。
そして、一緒に学習させる画像はcifar-10です。
さらに、実行速度が要求されるため、MobileNetV2は使いません。
さらに軽量な自作モデルで学習させました。
alpha = 5
inputs = Input(shape=x_train.shape[1:])
c = Conv2D(64, (1, 1), padding="same")(inputs)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(64, (3, 3), padding="same")(c)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(64, (3, 3), padding="same")(c)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(64, (3, 3), strides=2)(c)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(128, (3, 3), padding="same")(c)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(128, (3, 3), padding="same")(c)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(128, (3, 3), strides=2)(c)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(256, (3, 3), padding="same")(c)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(256, (3, 3), padding="same")(c)
c = BatchNormalization()(c)
c = Activation("relu")(c)
c = Conv2D(256, (3, 3), strides=2)(c)
c = BatchNormalization()(c)
c = Activation("relu", name="out")(c)
c = GlobalAveragePooling2D()(c)
c = keras.layers.Lambda(lambda xx: alpha*(xx)/K.sqrt(K.sum(xx**2)))(c) #metric learning
c = Dense(classes, activation='softmax')(c)
結果
ここでは一回しか実験していません。
また、異常スコアの算出は実行速度が要求されるため、3種類の方法で試してみました。
AUCは以下のとおりです。
| KNN(LOF) | ユークリッド距離 | マハラノビス距離 | |
|---|---|---|---|
| 異常検知 | 0.75 | 0.73 | 0.85 |
| 弱異常検知 | 0.81 | 0.76 | 0.88 |
意外にもマハラノビス距離が一番良い結果となりました。
LOFは正常画像が少ないため、過学習が起きた可能性があります。
ただ、LOFよりマハラノビス距離の方が実行速度が速いため、一石二鳥な感じもします。
気になる実行速度は次の記事で書きます。
どちらにしても、異常検知より弱異常検知の方が良い結果となりました。
弱異常検知の特徴
-
精度向上の効果
弱異常検知の効果は、「異常画像の内容」や「metric learningの種類」によって変わるかと思います。
色々試してみてください。 -
異常の重み
「この異常モードだけは検知させたい」といった異常の重みがあったとしたら、弱異常検知に
その画像を突っ込むことで、強力に異常検知してくれると思います。
食料品の世界では、金属片の混入は重大クレームにつながるので、こういった重みが付けられるのは
実用的かもしれません。 -
異常データの数
異常画像の「量」と「種類」は多いに越したことはありません。それに比例して精度も上がると思います。 -
応用範囲
今回は画像しか扱っていませんが、音データでも効果があると思われます。
いわゆるテーブルデータでも効果があるかは未知数です。
まとめ
- 少量の異常データを入れた「弱異常検知」は、通常の異常検知より精度が上がる。
- 最終的な異常スコアは、ユークリッド距離やマハラノビス距離、KNN、cos類似度等で算出され、これらは選択肢が多いため「精度」と「実行速度」を見ながら決めると良い。