こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、SVM(Support Vector Machine)をおさらいします。
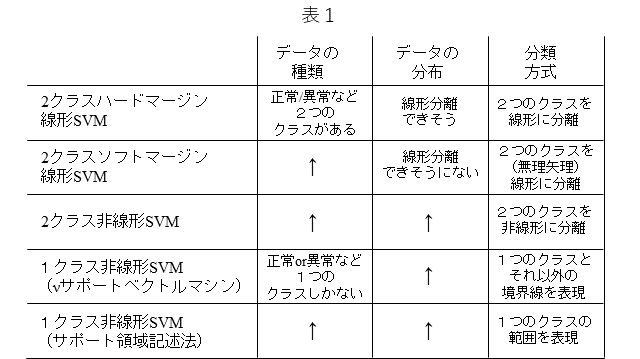
表1は、代表的なSVMをまとめています。SVMはクラス分類器ですが、データの種類、データの分布、分類方式に応じて、適切なSVMを選ぶことができます。また、SVMは、説明性に優れる一方で、ディープラーニングなどのカッティング・エッジな手法と比較しますとその精度は劣るというのが一般的な評価ではないかと思います。しかし、SVMは前記のように説明性に優れることに加え、その学習は、凸最適化問題に帰着することから、大域最適解であることが保証されるなど、理論的には魅力的なところが多々あります。凸最適化問題は、局所解と大域最適解が同一である解空間での最適化問題で、局所解が複数存在するような最適化問題より容易に最適化が可能です。表中に示されますように、SVMには、さまざまな形態がありますが、いずれもラグランジュの双対問題における最適化パラメータを用いて、識別線(面)の数式が表されます。今回は、その形を比較することでSVMを俯瞰してみます。
1. はじめに
SVMには、いくつかの種類があります。以下に簡単にまとめます。
・分類と回帰の機能がある。
・分類機能には下記がある。
- 線形SVMと非線形SVMがある。
- 1クラス SVMと2クラスSVMがある。
- 2クラスSVMには、ハードマージンSVMとソフトマージンSVMがある。
・回帰機能には下記がある。
- 線形SV回帰と非線形SV回帰がある。
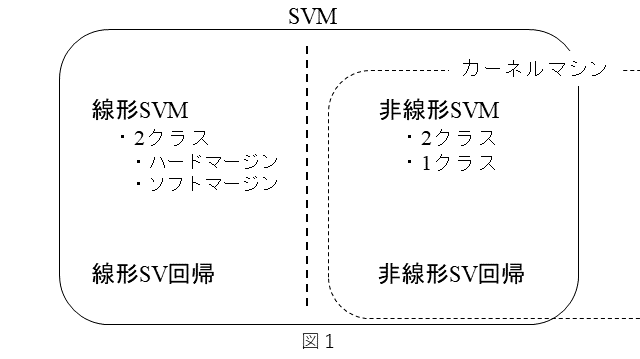
非線形SVMおよび非線形SV回帰は、カーネル関数を用いますので、カーネルマシンとして扱われることもあります。以上を図1にまとめてみました。
SVMを体系的に理解するには、次の順序で進めて行くのが良いのではないかと思います。
- 分類器としての2クラスハードマージン線形SVM
↓
- 分類器としての2クラスソフトマージン線形SVM
↓
- 分類器としての2クラス非線形SVM
↓
- 分類器としての1クラス非線形SVM
↓
- 回帰としての線形SV回帰/非線形SV回帰
今回は、「1. 分類器としての2クラスハードマージン線形SVM」~「4. 分類器としての1クラス非線形SVM」がいずれもラグランジュの双対問題に基づく最適化問題に帰着することを示して、その形を比較することでSVMという分類器の性質を俯瞰してみます。
2. どのような分類を考えるのか?
2.1 2クラスハードマージン線形SVM
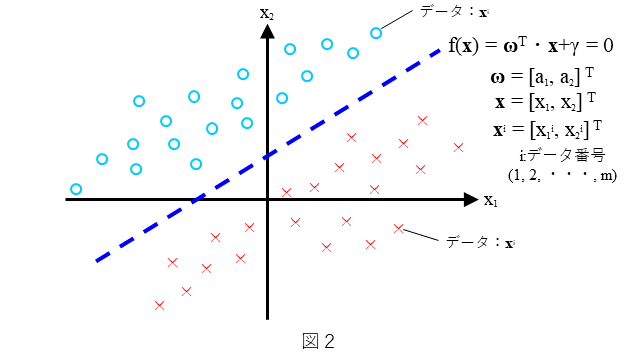
まず、2クラスハードマージン線形SVMを簡単におさらいしておきます。分類器としての2クラスハードマージン線形SVMは、どのような分類を考えるのか、を図2に示します。わかりやすいように2次元で表しています。直線 $f({\bf x})={\bf\omega}^{T} \cdot {\bf x} + \gamma=0$ によりデータが(○と×に)2分可能なデータの分布を考えます。ここで、データの分布は図2にありますように直線で分離可能な分布とします(ハードマージンは、このような分布を前提としています)。${\bf x}$が○のときは $f({\bf x})>0$ となり、${\bf x}$が×のときは $f({\bf x})<0$ となるような $f({\bf x})$ を求めること、すなわち、$\bf{\omega}$ と $\gamma$ を決めることを考えます。
2.2 2クラスソフトマージン線形SVM
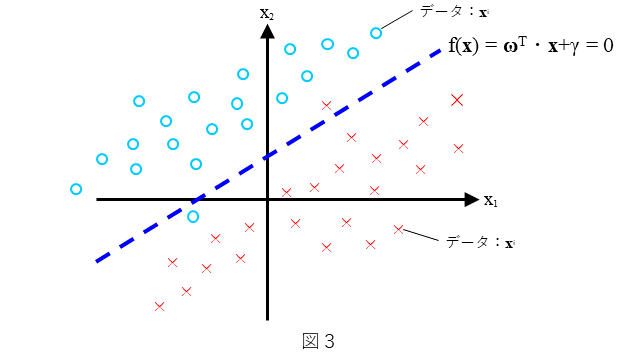
次に、2クラスソフトマージン線形SVMを簡単におさらいしておきます。分類器としての2クラスソフトマージン線形SVMは、どのような分類を考えるのか、を図3に示します。わかりやすいように2次元で表しています。直線 $f({\bf x})={\bf\omega}^{T}{\bf x} + \gamma=0$ によりデータが、できるだけ(○と×に)2分可能なデータの分布を考えます。ここで、データの分布は図2にありますように直線で全てのデータが分離することはできないような分布とします(ソフトマージンは、このような分布を前提としています)。できるだけ多くの${\bf x}$に対して、${\bf x}$が○のときは $f({\bf x})>0$ となり、${\bf x}$が×のときは $f({\bf x})<0$ となるような $f({\bf x})$ を求めること、すなわち、${\bf\omega}$ と $\gamma$ を決めることを考えます。
2.3 2クラス非線形SVM
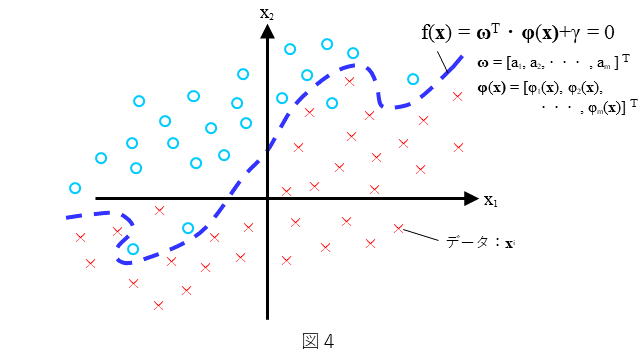
次に、2クラス非線形SVMを簡単におさらいしておきます。分類器としての2クラス非線形SVMは、どのような分類を考えるのか、を図4に示します。わかりやすいように2次元で表しています。(1)式で示される曲線 によりデータができるだけ(○と×に)2分可能なデータの分布を考えます。
$$
f({\bf x}),=,{\bf \omega}^T{\bf\phi}({\bf x}),+,\gamma = 0\hspace{1cm}・・・(1)
$$
ここに、${\bf\phi}(\bf{x})$ は、図中にもありますが(2)式で示されるように、非線形関数$\phi_k({\bf x})$ のベクトルで表されます。
$$
{\bf\phi}({\bf x})=[,\phi_1({\bf x}),,\phi_1({\bf x}),,\cdots,,\phi_m({\bf x}),]\hspace{1cm}・・・(2)
$$
すなわち、(1)式で表される曲線は、非線形関数 $\phi_k({\bf x})$ の線形結合です。ここで、データの分布は図4にありますようにある曲線で全てのデータが分離することはできないような分布とします。できるだけ多くの ${\bf x}$ に対して、${\bf x}$ が○のときは $f({\bf x})>0$ となり、${\bf x}$ が×のときは $f({\bf x})<0$ となるような $f({\bf x})$ を求めること、すなわち、$\bf{\omega}$ と $\gamma$ を決めることを考えます。
2.4 1クラス非線形SVM(1クラスνサポートベクトルマシン)
次に、1クラス非線形SVMの代表的な1形態であります1クラス$\nu$サポートベクトルマシンを簡単におさらいしておきます。1クラス非線形SVMは、1クラスの名称が指してますように、データのクラスは一つしかない状態を前提とします。前節までに示しました図2、図3もしくは図4に基づけば、○もしくは×のどちらかしかない状態を指します。1クラスのデータだけで分類を行うということは、得られている一つのクラスのデータだけでなんらかの領域を定義し、その領域内にあるデータとその領域外にあるデータで分類するというものです。
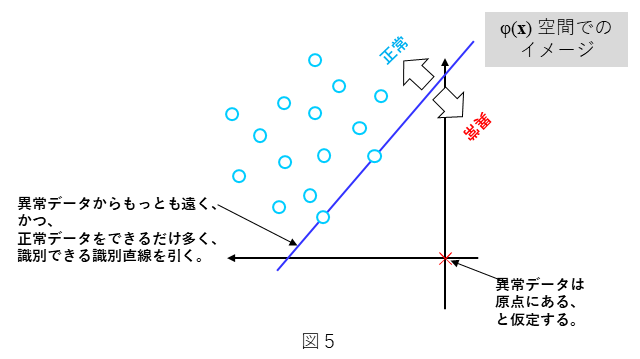
図5は、1クラス$\nu$サポートベクトルマシンの考え方を示しています。1クラス$\nu$サポートベクトルマシンは、直線を境に○と×を分類するものです。図5においては、○を正常データとし、×を仮想異常データとしています。これは、一般に正常データを比較的多量に収集することが可能ですが、その一方で、異常データは得られにくいことが多いことを想定しています。すなわち、○の正常データを用いた1クラス非線形SVMを考えています。なお、図5は、データ $\bf x$ を非線形関数 $\phi({\bf x})$ で射像した空間における表現です。すなわち元空間であるデータ $\bf x$ の空間では、図5における直線も非線形な形となります。また、図5は、2次元で表していますが、3次元以上でも同様の考え方が適用されます。その場合は、直線は超平面となります。
このとき、識別直線は、次のi)とii)の条件を満たすように決めます。
i) 識別直線は、異常データ×からできるだけ遠ざかるようにする。
ii) 正常データ○は、できるだけ多く、識別直線の上側に存在するようにする。
この条件i)はできるだけ直線を原点から遠ざけることを意味し、条件ii)はできるだけ直線を原点に近づけることを意味しますので、両条件はトレードオフの関係にあります。
2.5 1クラス非線形SVM(サポートベクトル領域記述法)
次に、1クラス非線形SVMのもう一つの代表的な1形態でありますサポートベクトル領域記述法を簡単におさらいしておきます。
図6は、サポートベクトル領域記述法の考え方を示しています。サポートベクトル領域記述法は、円の内側と外側で○と×を分類するものです。なお、図6は、図5と同じく、データ $\bf x$ を非線形関数 $\phi({\bf x})$ で射像した空間における表現です。すなわち元空間であるデータ $\bf x$ の空間では、図6における円も非線形な形となります。また、図6は、2次元で表していますが、3次元以上でも同様の考え方が適用されます。その場合は、円は超球となります。
このとき、円(中心と半径)は、次のi)とii)の条件を満たすように決めます。
i) 円周は、異常データ×からできるだけ遠ざかるようにする。
ii) 正常データ○は、できるだけ多く、円の内側に存在するようにする。
この条件i)はできるだけ円の半径をできるだけ小さくすることを意味し、条件ii)はできるだけ円の半径をできるだけ大きくすることを意味しますので、両条件はトレードオフの関係にあります。
3. どのような最適化問題に帰着するのか?
3.1 2クラスソフトマージン線形SVM
前章でご紹介しました各SVMの学習(パラメータ値の決定)は、2次計画問題の形となります。2次計画問題とは、目的関数が2次形式であり、制約条件が1次関数である最適化問題です。2次計画問題には様々な解法がありますが、SVMの場合は、2次計画問題を主問題として、それと対で存在するラグランジュの双対問題を解くのが一般的です。そして、このラグランジュの双対問題は、双対変数に関する最適化問題に帰着します。本章では、前章でご紹介しました様々なSVMがそれぞれどのような双対変数に関する最適化問題に帰着するかを示し、似たような形になるということをご紹介したいと思います。
まず、2クラスソフトマージン線形SVMがどのような双対変数に関する最適化問題に帰着するかを示します。前章でご紹介しました2クラスハードマージン線形SVMは、全てのデータが(○と×に)2分可能な特殊な2クラスソフトマージン線形SVMと解釈できますので、2クラスソフトマージン線形SVMのみを示します。(3)式と(4)式は、2クラスソフトマージン線形SVMの学習(パラメータ値の決定)を示した2次計画問題です。
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^iy^i{\alpha}^jy^j{{\bf x}^i}^T{\bf x}^j,+,\sum{\alpha}^i\hspace{1cm}・・・(3)
$$
$$
s.t.;{\alpha}^i\geq0,;\sum{\alpha}^iy^i=0,;C-{\alpha}^i={\mu}^i\geq0\hspace{1cm}・・・(4)
$$
ここに、$y^i$ は、下式で表されるように、学習データ ${\bf x}^i$( $i$:データ番号 ) ひとつひとつに付与される正解ラベルです。
$$
y^i=\left\{
\begin{array}{ll}
,+1(,{\bf x}^iが○のとき,) \
,-1(,{\bf x}^iが×のとき,) \
\end{array}
\right.
$$
また、$\alpha$ は、双対変数と呼ばれるパラメータで、係数 $C$ は、ソフトマージンの性質を調節するパラメータで、誤分類を許容させない程度を調節する係数と言えます。すなわち、係数 $C$ の値が大きいほど、誤分類が少なくなるように学習します。(3)式は、$\alpha^i$ に関する2次形式となっておりますので、$\alpha^i$ に関する凸最適化問題に帰着していることがわかります。(3)式と(4)式を解くことで、(5)式で示されるソフトマージン線形SVMの識別線の式が得られます。
$$
f({\bf x}),=,\sum{\alpha}^iy^i{{\bf x}^i}^T{\bf x},+,(,{y’}^i – \sum{\alpha}^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i,),=0\hspace{1cm}・・・(5)
$$
ここに、${\bf{x}'}^i$および${y'}^i$は、${\alpha}^i$の値が下記の条件を満たすときの ${\bf x}^i$ および ${y}^i$ です。
$$
\begin{array}{l}
,&{{\bf x}’}^i : 0 < {\alpha_l}^i < C,のときの,{\bf x}\
,&{y’}^i : 上記の{{\bf x}'}^iに対応した正解ラベル,y
\end{array}
$$
(5)式において、${\bf x}^i,,{{{\bf x}}'}^i$ は学習データであり、$y^i$ は正解ラベル、${\bf x}$ はテストデータです。(5)式をみますと、ソフトマージン線形SVMの識別線は、双対変数 $\alpha^i$ が決まれば、一意に決まることがわかります。なお、2クラスハードマージン線形SVMおよび2クラスソフトマージン線形SVMの詳細は、それぞれ別記事でまとめておりますので、ご興味のある方は、ご参考頂ければと思います。
3.2 2クラス非線形SVM
次に、2クラス非線形SVMがどのような双対変数に関する最適化問題に帰着するかを示します。(6)式と(7)式は、2クラス非線形SVMの学習を示した2次計画問題です。
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^iy^i{\alpha}^jy^jK({\bf x}^i,{\bf x}^j),+,\sum{\alpha}^i\hspace{1cm}・・・(6)
$$
$$
s.t.;{\alpha}^i\geq0,;\sum{\alpha}^iy^i=0,;C-{\alpha}^i={\mu}^i\geq0\hspace{1cm}・・・(7)
$$
ここに、 $K({\bf a},{\bf b})$ は、(8)式で定義される非線形関数の内積として表されるカーネル関数です。
$$
K({\bf a},{\bf b})={\bf\phi}({\bf a})^T{\bf\phi}({\bf b})\hspace{1cm}・・・(8)
$$
(6)式は、$\alpha^i$ に関する2次形式となっておりますので、$\alpha^i$ に関する凸最適化問題に帰着していることがわかります。(6)式と(7)式を解くことで、(9)式で示される2クラス非線形SVMの識別線の式が得られます。
$$
f({\bf x}),=,\sum\alpha^iy^iK({{\bf x}^i,, {\bf x}}),+,(,{y’}^i – \sum\alpha^i{y}^iK({{\bf x}^i},, {{{\bf x}'}^i}),)=0\hspace{1cm}・・・(9)
$$
ここに、${\bf{x}'}^i$ および ${y'}^i$ は、${\alpha}^i$ の値が下記の条件を満たすときの ${\bf x}^i$ および ${y}^i$ です。
$$
\begin{array}{l}
,&{{\bf x}’}^i : 0 < {\alpha_l}^i < C,のときの,{\bf x}\
,&{y’}^i : 上記の{{\bf x}'}^iに対応した正解ラベル,y
\end{array}
$$
(9)式において、${\bf x}^i,,{{{\bf x}}'}^i$ は学習データであり、$y^i$ は正解ラベル、${\bf x}$ はテストデータです。(9)式をみますと、2クラス非線形SVMの識別線は、双対変数 $\alpha^i$ が決まれば、一意に決まることがわかります。
2クラスソフトマージン線形SVMの学習を示した(3)式と2クラス非線形SVMの学習を示した(6)式を見比べますと、よく似ていることがわかります。(3)式において、${\bf x}^i$ → $\phi({\bf x}^i) $、${\bf x}^j$ → $\phi({\bf x}^j) $ と置き換えて、さらに、${\bf\phi}({{\bf x}^i})^T{\bf\phi}({\bf x}^j) → K({{\bf x}^i},, {{\bf x}}^j)$ と置き換えることで、(6)式が得られます。(4)式には、非線形の項 $\phi({\bf x}^j) $ が含まれないので、(4)式と(7)式は同じです。また、2クラスソフトマージン線形SVMの識別線の式であります(5)式と2クラス非線形SVMの識別線の式であります(9)式を見比べますと、同じく、よく似ていることがわかります。(5)式において、${\bf x}^i$ → $\phi({\bf x}^i) $、${{\bf x}'}^i$ → $\phi({{\bf x}'}^i) $、${\bf x}$ → $\phi({\bf x}) $ と置き換えて、さらに、${\bf\phi}({{\bf x}^i})^T{\bf\phi}({\bf x}) → K({{\bf x}^i},, {{\bf x}})$ 、${\bf\phi}({{\bf x}^i})^T{\bf\phi}({{{\bf x}'}^i}) → K({{\bf x}^i},, {{{\bf x}'}^i})$ と置き換えることで、(9)式が得られます。${\bf{x}'}^i$ および ${y'}^i$ の定義は、2クラスソフトマージン線形SVMと2クラス非線形SVMで同じです。
このように、2クラスソフトマージン線形SVMと2クラス非線形SVMは、良く似ていることがわかります。なお、2クラス非線形SVMの詳細は、別記事でまとめておりますので、ご興味のある方は、ご参考頂ければと思います。
3.3 1クラス非線形SVM(1クラスνサポートベクトルマシン)
次に、1クラス非線形SVMの1形態である1クラス$\nu$サポートベクトルマシンがどのような双対変数に関する最適化問題に帰着するかを示します。(10)式と(11)式は、1クラス$\nu$サポートベクトルマシンの学習を示した2次計画問題です。
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^i{\alpha}^jK({\bf x}^i,{\bf x}^j)\hspace{1cm}・・・(10)
$$
$$
s.t.;0\leq{\alpha}^i\leq\frac{1}{M\nu},;;\sum\alpha^i=1\hspace{1cm}・・・(11)
$$
ここに、$M$はデータ数(正常データ数)です。また、$\nu$ は、図5において、識別直線の位置を調節するためのパラメータです。その値が大きくなると、識別直線は原点(仮想異常データ×)から遠ざかり、その値が小さくなると、識別直線は原点(仮想異常データ×)に近づくようなパラメータです。(10)式および(11)式を解くことで、識別直線の式を表す(12)式が得られます。
$$
f(x) = \sum\alpha^i K({\bf x}^i, {\bf x}) - \sum\alpha^i K({\bf x}^i, {\bf x'}^i) = 0\hspace{1cm}・・・(12)
$$
${\bf{x}'}^i$は、${\alpha}^i$の値が下記の条件を満たすときの ${\bf x}^i$ です。
$$
{{\bf x}’}^i : 0 < \alpha^i < \frac{1}{M\nu},のときの,{\bf x}^i
$$
ここに、${\bf x}^i$ および ${{\bf x}'}^i$は学習データ、${\bf x}$ はテストデータです。(12)式をみますと、1クラス$\nu$サポートベクトルマシンの識別線は、双対変数 $\alpha^i$ が決まれば、一意に決まることがわかります。
2クラス非線形SVMの学習を示した(6)式と1クラス$\nu$サポートベクトルマシンの学習を示した(10)式を見比べますと、似ていることがわかります。(6)式において、$y^i=1$(全て正常データ) とし、 $\sum\alpha^i=1$( (11)式の制約条件 )とすると、(10)式が得られます。また、(9)式において、$y^i=1$ とすると、(12)式が得られます。
このように、2クラス非線形SVMと1クラス$\nu$サポートベクトルマシンも、似ていることがわかります。なお、1クラス$\nu$サポートベクトルマシンの詳細も、別記事でまとめておりますので、ご興味のある方は、ご参考頂ければと思います。
3.4 1クラス非線形SVM(サポートベクトル領域記述法)
次に、1クラス非線形SVMの1形態であるサポートベクトル領域記述法がどのような双対変数に関する最適化問題に帰着するかを示します。(13)式と(14)式は、サポートベクトル領域記述法の学習を示した2次計画問題です。
$$
\underset{{\alpha}^i}{max},-\frac{1}{\nu}\sum\sum{\alpha}^i{\alpha}^jK({\bf x}^i,{\bf x}^j)+\sum{\alpha}^i K({\bf x}^i,{\bf x}^i)\hspace{1cm}・・・(13)
$$
$$
s.t.;0\leq{\alpha}^i\leq\frac{1}{M},;;\sum{\alpha}^i=\nu\hspace{1cm}・・・(14)
$$
ここに、$M$はデータ数(正常データ数)です。また、$\nu$ は、図6において、円の半径の大きさを調節するためのパラメータです。その値が大きくなると、円の半径は小さくなり(仮想異常データ領域から遠ざかり)、その値が小さくなると、円の半径は大きくなる(仮想異常データ領域に近づく、あるいは包含する)ようなパラメータです。(13)式および(14)式を解くことで、円の中心 $\bf c$ と $\phi({\bf x})$(データ $\bf x$ を非線形関数 $\phi$ で射像した結果) との距離 $l$ の二乗値を与える(15)式が得られます。
$$
\begin{eqnarray}
l^2&=&||,{\bf\phi}({\bf x}),–,{\bf c},||^2\
\
&=&K({\bf x},{\bf x})-\frac{2}{\nu}\sum\alpha^iK({\bf x},{\bf x}^i)+\frac{1}{{\nu}^2}\sum\sum\alpha^i\alpha^jK({\bf x}^i,{\bf x}^j)\hspace{1cm}・・・(15)
\end{eqnarray}
$$
このとき、円の半径の二乗値 $R^2$ は、(15)式の ${\bf x}$ に、下記の条件を満たす ${{\bf x}'}^i$ を代入して得ます。
$$
{{\bf x}’}^i : 0 < \alpha^i < \frac{1}{M},のときの,{\bf x}
$$
上記の条件は、 ${{\bf x}'}^i$ が円周上にあることを意味し、いわゆるサポートベクトルであることを意味します。テスト時は、テストデータ ${\bf x}$ と円の中心の距離 $l$ の二乗値を(15)式から求めます。$l^2\leq R^2$ のとき、テストデータ ${\bf x}$ は、正常範囲である円の内側もしくは円周上にありますので、正常と判定します。$l^2>R^2$ のとき、テストデータ ${\bf x}$ は、正常範囲である円の外側にありますので、異常と判定します。2クラス非線形SVMの学習を示した(6)式とサポートベクトル領域記述法の学習を示した(13)式を見比べますと、よく似ていることがわかります。あるいは、1クラス$\nu$サポートベクトルマシンの学習を示した(10)式とサポートベクトル領域記述法の学習を示した(13)式を見比べてみても、よく似ていることがわかります。なお、サポートベクトル領域記述法の詳細も、別記事でまとめておりますので、ご興味のある方は、ご参考頂ければと思います。
4. まとめ
4.1 パラメータ値を決めるための最適化の式
前章で示しました各SVMのパラメータ値を決めるための最適化の式をまとめます。
・2クラスソフト-マージン線形SVM
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^iy^i{\alpha}^jy^j{{\bf x}^i}^T{\bf x}^j,+,\sum{\alpha}^i\hspace{1cm}・・・(3)
$$
$$
s.t.;{\alpha}^i\geq0,;\sum{\alpha}^iy^i=0,;C-{\alpha}^i={\mu}^i\geq0\hspace{1cm}・・・(4)
$$
・2クラス非線形SVM
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^iy^i{\alpha}^jy^jK({\bf x}^i,{\bf x}^j),+,\sum{\alpha}^i\hspace{1cm}・・・(6)
$$
$$
s.t.;{\alpha}^i\geq0,;\sum{\alpha}^iy^i=0,;C-{\alpha}^i={\mu}^i\geq0\hspace{1cm}・・・(7)
$$
・1クラス非線形SVM(1クラス$\nu$サポートベクトルマシン)
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^i{\alpha}^jK({\bf x}^i,{\bf x}^j)\hspace{1cm}・・・(10)
$$
$$
s.t.;0\leq{\alpha}^i\leq\frac{1}{M\nu},;;\sum\alpha^i=1\hspace{1cm}・・・(11)
$$
・1クラス非線形SVM(サポートベクトル領域記述法)
$$
\underset{{\alpha}^i}{max},-\frac{1}{\nu}\sum\sum{\alpha}^i{\alpha}^jK({\bf x}^i,{\bf x}^j)+\sum{\alpha}^i K({\bf x}^i,{\bf x}^i)\hspace{1cm}・・・(13)
$$
$$
s.t.;0\leq{\alpha}^i\leq\frac{1}{M},;;\sum{\alpha}^i=\nu\hspace{1cm}・・・(14)
$$
あらためて、各SVMの最適化の式は、お互いによく似ていることがわかります。
4.2 識別線の式
同様に、前節で示した最適化の式により最適化したパラメータ値を用いた識別線別線の式をまとめます。
・2クラスソフト-マージン線形SVM
$$
f({\bf x}),=,\sum{\alpha}^iy^i{{\bf x}^i}^T{\bf x},+,(,{y’}^i – \sum{\alpha}^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i,),=0\hspace{1cm}・・・(5)
$$
・2クラス非線形SVM
$$
f({\bf x}),=,\sum\alpha^iy^iK({{\bf x}^i,, {\bf x}}),+,(,{y’}^i – \sum\alpha^i{y}^iK({{{\bf x}'}^i},, {\bf x}),)=0\hspace{1cm}・・・(9)
$$
・1クラス非線形SVM(1クラス$\nu$サポートベクトルマシン)
$$
f(x) = \sum\alpha^i K({\bf x}^i, {\bf x}) - \sum\alpha^i K({\bf x}^i, {\bf x'}^i) = 0\hspace{1cm}・・・(12)
$$
・1クラス非線形SVM(サポートベクトル領域記述法)
$$
l^2=K({\bf x},{\bf x})-\frac{2}{\nu}\sum\alpha^iK({\bf x},{\bf x}^i)+\frac{1}{{\nu}^2}\sum\sum\alpha^i\alpha^jK({\bf x}^i,{\bf x}^j)\hspace{1cm}・・・(15)
$$
サポートベクトル領域記述法における式は、識別線ではなく、距離を示していますので、数式の形は、その他のSVMの数式とは、やや異なりますが、2クラスソフト-マージン線形SVM、2クラス非線形SVM、1クラス$\nu$サポートベクトルマシンの識別線の式は、お互いによく似ていることがわかります。
5. おわりに
今回は、さまざまなSVMがいずれも帰着するラグランジュの双対問題の形とその双対問題における最適化パラメータを用いた識別線の数式を俯瞰し、それらがお互いによく似ていることをご紹介しました。本記事でご紹介しました内容のようにSVMを整理しておきますと、頭の中でうまくSVMを収めておくことができるかもしれません。なお、本文中でも述べておりますが、本記事でご紹介しました様々なSVMの詳細は、それぞれ記事にまとめておりますので、ご興味のある方は、ご参考頂ければと思います。
SVMをおさらい(ハードマージン線形SVMの編) - Qiita
SVMをおさらい(ソフトマージン線形SVMの編) - Qiita
SVMをおさらい(2クラス非線形SVMの編) - Qiita
SVMをおさらい(1クラスνサポートベクトルマシンの編) - Qiita
SVMをおさらい(サポートベクトル領域記述法の編) - Qiita
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
竹内 一郎、鳥山昌幸:サポートベクトルマシン
赤穂昭太郎:カーネル多変量解析