こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、SVM(Support Vector Machine)をおさらいします。
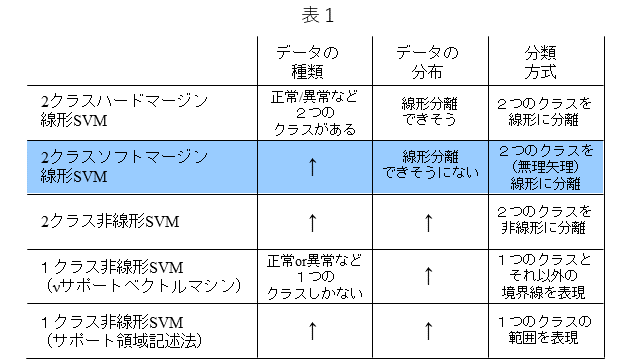
表1は、代表的なSVMをまとめています。SVMはクラス分類器ですが、データの種類、データの分布、分類方式に応じて、適切なSVMを選ぶことができます。また、SVMは、説明性に優れる一方で、ディープラーニングなどのカッティング・エッジな手法と比較しますとその精度は劣るというのが一般的な評価ではないかと思います。しかし、SVMは前記のように説明性に優れることに加え、その学習は、凸問題に帰着することから、大域最適解であることが保証されるなど、理論的には魅力的なところが多々あります。表中のSVMから、今回は2クラスソフトマージン線形SVMと呼ばれるSVMについておさらいします。
1. はじめに
SVMには、いくつかの種類があります。以下に簡単にまとめます。
・分類と回帰の機能がある。
・分類機能には下記がある。
- 線形SVMと非線形SVMがある。
- 1クラス SVMと2クラスSVMがある。
- 2クラスSVMには、ハードマージンSVMとソフトマージンSVMがある。
・回帰機能には下記がある。
- 線形SV回帰と非線形SV回帰がある。
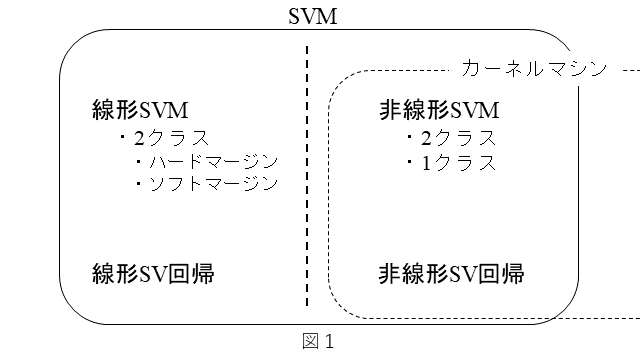
非線形SVMおよび非線形SV回帰は、カーネル関数を用いますので、カーネルマシンとして扱われることもあります。以上を図1にまとめてみました。
SVMを体系的に理解するには、次の順序で進めて行くのが良いのではないかと思います。
1. 分類器としての2クラスハードマージン線形SVM
↓
2. 分類器としての2クラスソフトマージン線形SVM
↓
3. 分類器としての2クラス非線形SVM
↓
4. 分類器としての1クラス非線形SVM
↓
5. 回帰としての線形SV回帰/非線形SV回帰
今回は、「2. 分類器としての2クラスソフトマージン線形SVM」について、おさらいします。
2. 2クラスハードマージン線形SVMを簡単におさらい
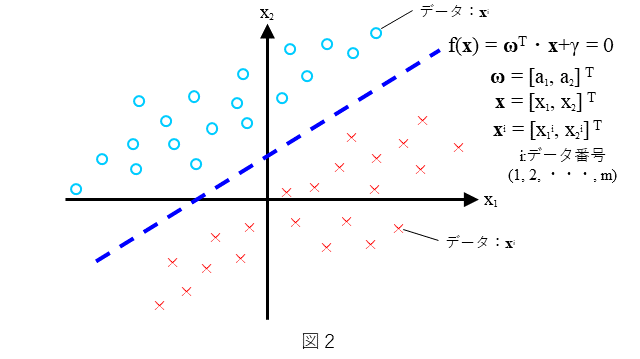
まず、2クラスハードマージン線形SVMを簡単におさらいしておきます。分類器としての2クラスハードマージン線形SVMは、どのような分類を考えるのか、を図2に示します。わかりやすいように2次元で表しています。直線 $f({\bf x})={\bf\omega}^{T} \cdot {\bf x} + \gamma=0$ によりデータが(○と×に)2分可能なデータの分布を考えます。ここで、データの分布は図2にありますように直線で分離可能な分布とします(ハードマージンは、このような分布を前提としています)。${\bf x}$が○のときは$f({\bf x})>0$ となり、${\bf x}$が×のときは$f({\bf x})<0$ となるような $f({\bf x})$ を求めること、すなわち、$\bf{\omega}$ と $\gamma$ を決めることを考えます。
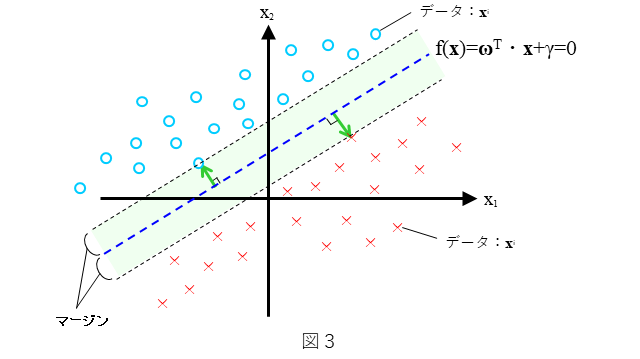
具体的には、図3で示されるような直線 $f({\bf x})=0$ に対するマージンを考え、そのマージンが最大化するような直線を考えます。マージンを最大化するような直線 $f({\bf x})=0$ とは、直線 $f({\bf x})=0$ からもっとも近い○と×それぞれから直線 $f({\bf x})=0$ に垂線を下ろしたとき、双方の垂線の長さが同時に最大となる(=等しくなる)ような直線 ${f({\bf x})=0}$ であり、このような直線は一意に決まります。このとき直線 ${f({\bf x})=0}$ をハードマージン線形SVMと呼びます。
(1)式と(2)式は、上記の条件を満たす直線 $f({\bf x})={\bf \omega}^T{\bf x}+\gamma = 0$ を求めるための条件です。
$$
\begin{array}{l}
,&y^i\cdot({\bf \omega}^T{\bf x}^i+\gamma)\geq 1 \hspace{1cm}・・・(1)\
,&\underset{{\bf \omega};\gamma}{min};||{\bf \omega}||^2\hspace{1cm}・・・(2)
\end{array}
$$
ここで、$y^i$ は、下式で表されるように、学習データ ${\bf x}^i$ ひとつひとつに付与される正解ラベルです。
$$
y^i=\left\{
\begin{array}{ll}
,+1(,{\bf x}^iが○のとき,) \
,-1(,{\bf x}^iが×のとき,) \
\end{array}
\right.
$$
(1)式は、図3中の上側のマージン直線において、直線上もしくはそれより上側に全ての○が存在しているということ、あるいは、下側のマージン直線において、直線上もしくはそれより下側に全ての×が存在しているということを意味しています。また、(2)式は、図3中のマージンが直線 $f({\bf x})=0$ からもっとも近い○と×それぞれから直線 $f({\bf x})=0$ に垂線を下ろしたとき、双方の垂線の長さが同時に最大となる(=等しくなる)ような○と×までの距離であることを意味しています。
上述したように、2つのマージン直線上もしくはそれより(いわば)外側に全てのデータ ${\bf x}^i $ は存在するようにマージン直線および直線 $f({\bf x})=0$ は決められます。したがって、テストデータを適用したときは、$f(\bf x)\geq1$ のとき、そのテストデータは○に分類されと判断し、$f({\bf x})\leq-1$ のとき、そのテストデータは、×に分類されたと判断することになります。2つのマージン直線に挟まれた領域に相当する $-1 (1)式と(2)式の2つの式は、2次計画問題と言われる形をしています。2次計画問題とは、目的関数(ここでは(2)式)が2次形式であり、制約条件(ここでは(1)式)が1次関数である最適化問題です。2次計画問題には様々な解法がありますが、SVMの場合は、ラグランジュの双対問題として最適化するのが一般的です。SVMのパラメータ最適化をラグランジュの双対問題として解く手順については後述します。
3. どのような分類を考えるのか?
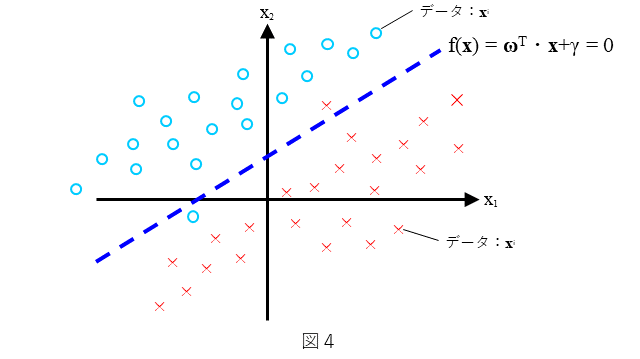
分類器としての2クラスソフトマージン線形SVMは、どのような分類を考えるのか、を図4に示します。わかりやすいように2次元で表しています。直線 $f({\bf x})={\bf\omega}^{T} \cdot {\bf x} + \gamma=0$ によりデータが、できるだけ(○と×に)2分可能なデータの分布を考えます。ここで、データの分布は図4にありますように直線で全てのデータが分離することはできないような分布とします(ソフトマージンは、このような分布を前提としています)。できるだけ多くの${\bf x}$に対して、${\bf x}$が○のときは$f({\bf x})>0$ となり、${\bf x}$が×のときは$f({\bf x})<0$ となるような $f({\bf x})$ を求めること、すなわち、$\bf{\omega}$ と $\gamma$ を決めることを考えます。
4. 定式化:ハードマージンとソフトマージンの違い
4.1 制約条件
2章で示しました(1)式の制約条件と(2)式の最適化が、ソフトマージンではハードマージンに対して、それぞれどのように変わるのか、という観点で説明していきます。まず、制約条件について説明します。ハードマージンの制約条件である(1)式に対して、ソフトマージンの制約条件は(3)式となります。
$$
\begin{array}{l}
,&y^i\cdot({\bf \omega}^T{\bf x}^i+\gamma)\geq 1-\xi^i \hspace{1cm}・・・(3)\
,&;(\xi^i\geq0)
\end{array}
$$
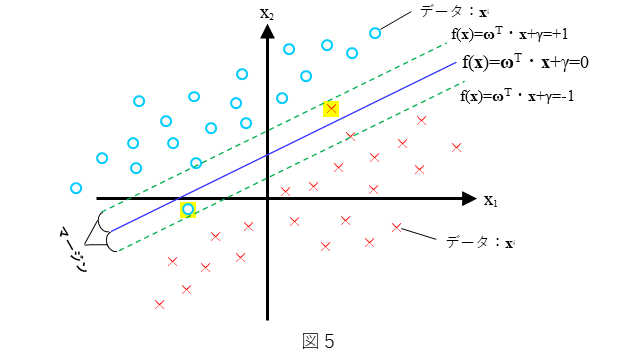
ハードマージンの制約条件である(1)式とソフトマージンの制約条件である(3)式を見比べますと、右辺の値が異なっています。具体的には、ハードマージンでは右辺の値が1であるのに対して、ソフトマージンでは $1-\xi^i$ となっています。2章で述べましたように、(1)式は、図3中の上側のマージン直線において、直線上もしくはそれより上側に全ての○が存在しているということ、あるいは、下側のマージン直線において、直線上もしくはそれより下側に全ての×が存在しているということを意味しています。より詳しくは、図5に示されるように、上側のマージン直線は(4)式で表され、下側のマージン直線は(5)式で表されます。
$$
\begin{array}{l}
,&{\bf \omega}^T{\bf x}^i+\gamma=+1\hspace{1cm}・・・(4)\
,&{\bf \omega}^T{\bf x}^i+\gamma=-1\hspace{1cm}・・・(5)
\end{array}
$$
このとき(4)式で表されるマージン直線上もしくはそれより上側に全ての○が存在しているということを数式で表現すると、$y^i=1$ かつ $({\bf \omega}^T{\bf x}^i+\gamma)\geq 1$ なので、(1)式で表されます。また、(5)式で定義されるマージン直線上もしくはそれより下側に全ての×が存在しているということを数式で表現すると、×のデータを正しく分類できているときは、$y^i=-1$ かつ $({\bf \omega}^T{\bf x}^i+\gamma)\leq-1$ なので、○のときと同じく(1)式で表されます。
これを踏まえて(3)式をあらためて見てみますと、(3)式の右辺は、$1-\xi^i,(\xi^i\geq0)$ ですので、$\xi^i>0$ のとき、(3)式の左辺は1より小さい値になり得ます。これは、$i$番目のデータが○ ($y^i=1$)であれば、(4)式で表されるマージン直線より下側に存在し得ることを意味し、あるいは、$i$番目のデータが×($y^i=-1$)であれば、(5)式で表されるマージン直線より上側に存在し得ることを意味します。すなわち、$\xi^i>0$ のとき、$i$番目のデータは正しく分類できていないことを意味します。なお、$\xi^i=0$ のときは、(3)式の左辺は、1以上の値になりますので、ハードマージンであり、正しく分類されています。このように、ソフトマージンにおける制約条件である(3)式は、いくつかの$x^i$に対して誤分類を許容するようになっています。
4.2 最適化
次に、最適化について説明します。ハードマージンの最適化の式である(2)式に対して、ソフトマージンの制約条件は(6)式となります。
$$
\underset{{\bf \omega},;\gamma}{min};\frac{1}{2}||{\bf \omega}||^2+C\sum\xi^i\hspace{1cm}・・・(6)
$$
ハードマージンの最適化の式である(2)式とソフトマージンの最適化の式である(6)式を見比べますと、第1項に係数1/2が係り、第二項の $C\sum\xi^i$ が追加されています。第1項の係数1/2は、微分に備えて便宜的に追加された係数であり、最小化にあたり影響を与えることはありません。第2項は、$\xi^i$ の和に係数 $C$ が係っています。$\xi^i$ は、上述しましたように、$\xi^i>0$ のとき、$i$番目のデータは正しく分類できておらず、$\xi^i$ の値が大きいほど、マージン直線に対して誤分類の領域に深く入っていくことを意味します。つまり、$\xi^i$ の値が大きいほど、誤分類の程度が大きくなっていくと言えます。したがって、誤分類の程度が大きいほど、その総和である $\sum\xi^i$ は大きくなりますので、(5)式で示される制約条件でいくつかの$x^i$に対して誤分類を許容する一方で、(6)式の第二項で、無制限に誤分類を許容することを制約していると言えます。係数 $C$は、誤分類を許容させない程度を調節する係数と言えます。例えば、係数 $C$ の値が∞のとき、すべての $\xi^i$は、0でなければならなく、このときハードマージンとなります。逆に係数 $C$ の値が0のとき、すべての $\xi^i$は、$0\leq0\leq∞$ の任意の値を取ることが出来て、無制限に誤分類を許容することになります。
以上で、前章で示しました(1)式の制約条件と(2)式の最適化が、ソフトマージンではハードマージンに対して、それぞれどのように変わるのか、という観点で説明しました。具体的には、ソフトマージンにおける制約条件は(3)式で表され、最適化は(6)式で表されます。
(3)式と(6)式の2つの式は、ハードマージンと同様に、2次計画問題と言われる形をしています。上述しましたように、2次計画問題とは、目的関数(ここでは(6)式)が2次形式であり、制約条件(ここでは(3)式)が1次関数である最適化問題です。2次計画問題には様々な解法がありますが、SVMの場合は、ラグランジュの双対問題として最適化するのが一般的です。SVMのパラメータ最適化をラグランジュの双対問題として解く手順は次章で述べます。
5. ラグランジュの双対問題を使って解く
5.1 解法の流れ
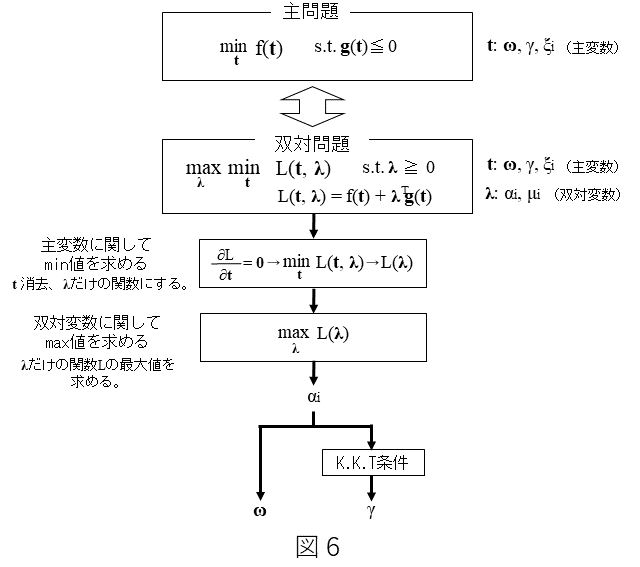
SVMのパラメータ最適化をラグランジュの双対問題として解く手順について説明します。図6は、解法の流れを示しています。まず主問題(ここでは、(3)式と(6)式)が与えられた時、これと対で存在します双対問題を定義します。ラグランジュの双対問題とは、この双対問題を解くことで主問題の解を求めるものです。これは、主問題を解くより双対問題を解く方法が一般的に容易だからです。
双対問題は、主問題における最適化変数である主変数と双対問題で追加される最適化変数である双対変数を変数として持つラグランジュ関数と呼ばれる関数と双対変数の制約条件からなります。詳細の証明は省きますが、このラグランジュ関数を主変数に関して最小かつ双対変数に関して最大となる点(鞍点)が、主問題の最適解となります。
解法の順序としては、まず、主変数に関してラグランジュ関数の最小値を求めることで双対変数のみの関数の形にした後、双対変数のみの関数が最大値となる双対変数の値を求めます。そして、この双対変数の値から、ラグランジュ関数を主変数に関して最小化する主変数の値(点)を求めることで、主問題の解を得ます。一見、双対問題にすることで、むしろ問題が複雑化するように思えますが、後述するように、主問題を解くより容易に解を得ることができます。以下、(3)式と(6)式をラグランジュの双対問題として解くプロセスの要点を説明していきます。
5.2 主問題
主問題は、(7)式の最適化と(8)式の制約条件で表されます。
$$
\begin{array}{l}
,&\underset{{\bf t}}{min};f({\bf t})\hspace{1cm}・・・(7)\
,&,, s.t. ,{\bf g}({\bf t})\leq0\hspace{1cm}・・・(8)
\end{array}
$$
上記の主問題に、(3)式と(6)式で表されるソフトマージン線形SVMの最適化問題を当てはめますと、(7)式が(6)式に、(8)式が(3)式にそれぞれ対応しますので、(9)式と(10)式となります。
$$
\underset{{\bf\omega},,\gamma,,\xi^i}{min};\frac{1}{2}||{\bf\omega}||^2+C\sum{\xi^i}\hspace{1cm}・・・(9)\
$$
$$
s.t.,-y^i ・({\bf\omega}^Tx^i+\gamma)+1-\xi^i\leq0,;;-\xi^i ≦ 0
\hspace{1cm}・・・(10)
$$
なお、${\bf t}$は、主変数で、(7)式が(6)式に対応することから、${\bf t}=({\bf\omega},\gamma, \xi^i)$ です。
5.3 双対問題
前節で、主問題を定義しました。本節では主問題に対する双対問題を定義します。(7)式および(8)式で定義される主問題に対する双対問題は、(11)式と(12)式で定義されます。
$$
\begin{array}{l}
,&\underset{{\bf \lambda}}{max},\underset{{\bf t}}{min};L({\bf t}, {\bf \lambda})\hspace{1cm}・・・(11)\
,& ,,s.t.,{\bf \lambda}\geq0\hspace{1cm}・・・(12)
\end{array}
$$
ここに、$L({\bf t},{\bf\lambda})$ は、ラグランジュ関数であり、(13)式で表されます。
$$
L({\bf t},{\bf \lambda})=f({\bf t}) + {\bf \lambda},{\bf g}({\bf t})\hspace{1cm}・・・(13)
$$
${\lambda}$ は、双対変数で、${\bf \lambda}=(\alpha^i, u^i)$ です。
(9)式と(10)式で表されるソフトマージン線形SVMの主問題からラグランジュ関数$L$は、(14)式で表されます。
$$
L(\omega, \gamma, \xi^i, \alpha^i, \mu^i) =\frac{1}{2}||{\bf\omega}||^2+C\sum{\xi^i}-\sum \alpha^i\left(,y^i ・({\bf\omega}^Tx^i+\gamma)-1+\xi^i,\right)-\sum\mu^i\xi^i\hspace{1cm}・・・(14)
$$
なお、双対変数である$\lambda$は、${\bf \lambda}=(\alpha^i, \mu^i)$ です。また、(14)式から、(9)式と(10)式で表されるソフトマージン線形SVMの主問題に対する双対問題は、(15)式および(16)式となります。
$$
\underset{\alpha^i,,\mu^i}{max},,\underset{{\bf\omega},,\gamma,,\xi^i}{min};\frac{1}{2}||{\bf\omega}||^2+C\sum{\xi^i}-\sum \alpha^i\left(,y^i ・({\bf\omega}^Tx^i+\gamma)-1+\xi^i,\right)-\sum\mu^i\xi^i\hspace{1cm}・・・(15)
$$
$$
s.t.;\alpha^i\geq0,;\mu^i\geq0\hspace{1cm}・・・(16)
$$
5.4 主変数に関してラグランジュ関数を最小化
前節で双対問題を定義しました。本節では定義した双対問題において、主変数に関してラグランジュ関数の最小値を求めます(双対変数のみの関数の形にします)。(14)式を主変数に関して偏微分すると、(17)式、(18)式、(19)式が得られます。
$$
\frac{\partial L}{\partial{\bf\omega}}={\bf\omega}-\sum\alpha^iy^i{\bf x}^i=0\hspace{1cm}・・・(17)
$$
$$
\frac{\partial L}{\partial \gamma}=-\sum\alpha^i y^i=0\hspace{1cm}・・・(18)
$$
$$
\frac{\partial L}{\partial{\xi}^i}=C-\alpha^i-\mu^i=0\hspace{1cm}・・・(19)
$$
(17)式、(18)式、(19)式を満たすとき、主変数に関してラグランジュ関数は最小となります。このときのラグランジュ関数は、双対変数のみの関数となります。具体的には、主変数に関してラグランジュ関数が最小となる条件である(17)式、(18)式、(19)式から主変数について解いて、(14)式に代入しますと(20)式が得られます。
$$
\begin{eqnarray}
,&\underset{{\bf\omega},,\gamma,,\xi^i}{min};\frac{1}{2}||{\bf\omega}||^2+C\sum{\xi^i}-\sum \alpha^i\left(,y^i ・({\bf\omega}^T{\bf x}^i+\gamma)-1+\xi^i,\right)-\sum\mu^i\xi^i\
,&=-\frac{1}{2}\sum\alpha^iy^i{{\bf x}^i}^T,\sum\alpha^jy^j{\bf x}^j,+,\sum\alpha^i\hspace{1cm}・・・(20)
\end{eqnarray}
$$
(20)式は、双対変数のうち、$\alpha^i$だけの関数になっており、$\mu^i$が消去されていることにも注意しましょう。
5.5 双対変数に関してラグランジュ関数を最大化
前節で主変数に関して最小となるラグランジュ関数を求めました。本節では求めた関数を最大化する双対変数を求めます。(20)式および(15)式から、(21)式が得られます。
$$
\underset{\alpha^i}{max},-\frac{1}{2}\sum\alpha^iy^i{{\bf x}^i}^T,\sum\alpha^jy^j{\bf x}^j,+,\sum\alpha^i\hspace{1cm}・・・(21)
$$
$\alpha^i$ は、(18)式、(19)式も満たす必要がありますので、(16)式、(18)式および(19)式から(22)式が制約条件になります。
$$
s.t.;\alpha^i\geq0,;\sum\alpha^iy^i=0,;C-\alpha^i=\mu^i\geq0\hspace{1cm}・・・(22)
$$
前節でも述べましたが、(21)式は双対変数のうち $\alpha^i$ だけの2次関数ですので、(22)式の制約を考慮した凸問題に帰着したことがわかります。(21)式+(22)式の形であれば、様々なソルバーがありますので、それを適用して解くのも良いかと思います(SVMに特化したソルバーもあります)。なお、(21)式から最適化すべきパラメータである $\alpha^i$ の数は、データのレコード数だけあることがわかります。このことからSVMでは学習時の計算負荷が高くなる傾向にあります。
5.6 パラメータ(ωとγ)を求める(主変数に関しては最小かつ双対変数に関しては最大となる点)
5.6.1 ωを求める
前節でソフトマージン線形SVMは、(21)式および(22)式で表される凸問題に帰着することを示しました。(21)式および(22)式を解くことで、$\alpha^i$の値が得られます。本節では得られた$\alpha^i$から主変数である $\bf\omega$ と $\gamma$ を求めます。
まず、$\omega$ を求めます。(17)式より(23)式が得られます。
$$
{\bf\omega}=\sum\alpha^iy^i{\bf x}^i\hspace{1cm}・・・(23)
$$
(23)式からもわかりますように、$\omega$ は、$\alpha^i$ と $y^i$ と $\bf x^i$ の積の線形結合で表され、線形結合の項の数は、レコード数に等しいです。すべてのデータを考慮して決められていることが式からもわかります。
5.6.2 γを求める
次に、$\gamma$ を求めます。$\bf \omega$ は、ラグランジュ関数を $\bf\omega$ に関して偏微分した式である(17)式から得られましたが、$\gamma$ は、(17)式、(18)式、(19)式のいずれからも求めることはできないことがわかります。$\gamma$は、K.K.T条件(Karush-Kuhn-Tucker Condition)を用いて求めます。K.K.T条件は、(7)式と(8)式で表される制約付き最小化問題の解において成立する条件を示したものです。K.K.Tの詳細については、ここでは述べませんが、ポイントだけ言えば、(10)式、(16)式、(17)式、(18)式、(19)式および(24)式と(25)式が成立することを示しています。
$$
\begin{array}{l}
,&-\sum \alpha^i\left(,y^i ・({\bf\omega}^T{\bf x}^i+\gamma)-1+\xi^i,\right)=0\hspace{1cm}・・・(24)\
,&-\sum\mu^i\xi^i=0\hspace{1cm}・・・(25)
\end{array}
$$
(10)式は主問題における制約条件を示していますので、成立すると言えます。また、(16)式は双対問題における双対変数の制約条件を示していますので、成立すると言えます。また、(17)式、(18)式、(19)式は、ラグランジュ関数を主変数に関して最小化する条件ですので、(7)式と(8)式で表される制約付き最小化問題の解において成立する条件であると言えます。(20)式の左辺をみますと、(24)式および(25)式は第2項と第3項であり、双対変数に関する項です。第2項と第3項が0のとき、主問題の(9)式となりますので、同様に(7)式と(8)式で表される制約付き最小化問題の解において成立する条件であると言えます。
途中の計算は省略しますが、K.K.T条件の各式を用いることで、$\gamma$ は(26)式で得られます。
$$
\gamma = {y’}^i – \sum\alpha^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i\hspace{1cm}・・・(26)
$$
ここに、${\alpha_l}^i$ は、ラグランジュの双対問題で定義される双対変数です。また、${\bf{x}'}^i$および${y'}^i$は、${\alpha_l}^i$の値が下記の条件を満たすときの ${\bf x}^i$ および ${y}^i$ です。
$$
\begin{array}{l}
,&{{\bf x}’}^i : 0 < \alpha^i < C,のときの,{\bf x}\
,&{y’}^i : 上記の{{\bf x}'}^iに対応した正解ラベル,y
\end{array}
$$
満たす ${{\bf x}'}^i,,y'^i$ であれば、どのような ${{\bf x}'}^i,,y'^i$ であっても、理論上は(26)式で得られる $\gamma$ は一意に決まります。(26)式は、(27)式のようにも表せ、$y'^i$ は+1もしくは -1であることから、${{\bf x}'}^i$は、マージン直線上の点であることがわかります(マージン直線上の点である${{\bf x}'}^i$を用いて $\gamma$を決めているとも言えます)。
$$
\gamma = {y’}^i –,{\bf\omega}^T{{\bf x}'}^i\hspace{1cm}・・・(27)
$$
以上で、ソフトマージン線形SVMの直線の式 $f(\bf x)={\bf\omega}^T{\bf x}+\gamma$ のパラメータである $\bf\omega$ は(23)式から、$\gamma$ は、(26)式(もしくは(27)式)から得られることを御説明しました。
6. SVMのスパース性
前章で、ソフトマージン線形SVMのパラメータである $\bf\omega$ と $\gamma$ を求める式を導出しました。同じく前章でも述べましたが、(23)式から、$\omega$ は $\alpha^i$ と $y^i$ と ${\bf x}^i$ の積の線形結合で表され、その線形式の項の数は、レコード数に等しいことがわかります。レコード数が非常に多いと、それに応じて、その線形式の項の数も多くなることになります。ここで、(23)式で表される線形式の各項の性質を決める $\alpha^i$ の値の性質についてもご説明しておきます。前章で述べたK.K.T条件から ${\bf x}^i$ が存在している領域に応じて、$\alpha^i$ の値が、次のように変わります(決まります)。
i) マージン直線の外側に ${\bf x}^i$ がある場合
$$
\alpha^i=0
$$
です。なお、マージン直線の外側とは、(4)式で表されるマージン直線より上の領域もしくは、(5)式で表されるマージン直線より下の領域を指します。すなわち、マージン直線の外側にある ${\bf x}^i$ は、ソフトマージン線形SVMである直線 $f(\bf x)={\bf\omega^T}{\bf x}+\gamma$ の決定に寄与しないことを意味します。
ii) マージン直線上に ${\bf x}^i$ がある場合
$$
0<\alpha^i<C
$$
です。すなわち、マージン直線上にある ${\bf x}^i$ は、識別線(マージン線)の決定に寄与し、対応する $\alpha^i$ の値は $0<\alpha^i<C$ となります。。
iii)マージン直線の内側に ${\bf x}^i$ がある場合
$$
\alpha^i=C
$$
です。なお、マージン直線の内側とは、(4)式で表されるマージン直線より下の領域かつ(5)式で表されるマージン直線より上の領域を指します。すなわち、マージン直線上にある ${\bf x}^i$ は、識別線(マージン線)の決定に寄与しますが、対応する $\alpha^i$ の値は $C$ で固定されます 。
i)の条件を満たす ${\bf x}^i$ は、学習データの大部分を占めると考えられますので、$\alpha^i$ のほとんどは0であることがわかります。上述しましたように、(23)式から $\omega$ は $\alpha^i$ と $y^i$ と ${\bf x}^i$ の積の線形結合で表され、その線形式の項の数はレコード数に等しいですが、そのほとんどの項が0であるので、(23)式はスパースであることがわかります。マージン直線と直線 $f({\bf x})=0$ を決定するのに必要な ${\bf x}^i$ は、マージン直線上にある ${\bf x}^i$ とマージン直線の内側の ${\bf x}^i$ のみであるということであり、直感にも合う結果です。全ての ${\bf x}^i$ を考慮した最適化問題を解くのですが、マージン直線と直線を決めるために使っているのは、上記の条件ii)とiii)に相当する ${\bf x}^i$ だけになる、ということですね。
7. おわりに
今回は、ソフトマージン線形SVMと呼ばれるSVMについておさらいしました。ソフトマージン線形SVMの定式化をできるだけわかりやすいアプローチで紹介したつもりです。ハードマージン線形SVMと同じく、ソフトマージン線型SVMの機能もイメージしやすいのではないかと思いますが、これを数式で表そうとすると、結構大変と思われた方もいらっしゃるのではないでしょうか。SVMは、今回ご紹介しましたソフトマージン線形SVMの他に、ハードマージン線形SVM、非線形SVMなど、様々な形があります。これらについては他の記事で紹介しますので、ご興味のある方はご参考下さい。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
竹内 一郎、鳥山昌幸:サポートベクトルマシン
赤穂昭太郎:カーネル多変量解析