こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、SVM(Support Vector Machine)をおさらいします。
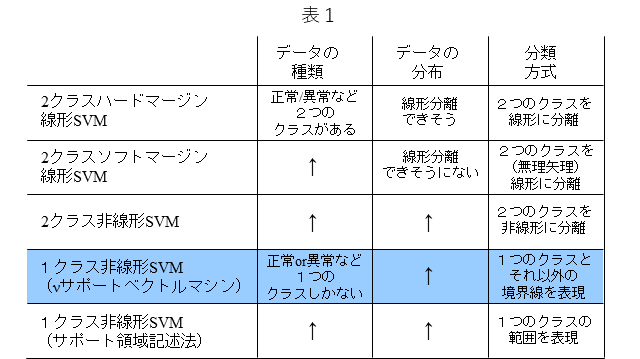
表1は、代表的なSVMをまとめています。SVMはクラス分類器ですが、データの種類、データの分布、分類方式に応じて、適切なSVMを選ぶことができます。また、SVMは、説明性に優れる一方で、ディープラーニングなどのカッティング・エッジな手法と比較しますとその精度は劣るというのが一般的な評価ではないかと思います。しかし、SVMは前記のように説明性に優れることに加え、その学習は、凸問題に帰着することから、大域最適解であることが保証されるなど、理論的には魅力的なところが多々あります。凸最適化問題は、局所解と大域最適解が同一である解空間での最適化問題で、局所解が複数存在するような最適化問題より容易に最適化が可能です。表中のSVMから、今回は、1クラス非線形SVMの中の1クラス$\nu$サポートベクトルマシンと呼ばれるSVMについておさらいします。
1. はじめに
SVMには、いくつかの種類があります。以下に簡単にまとめます。
・分類と回帰の機能がある。
・分類機能には下記がある。
- 線形SVMと非線形SVMがある。
- 1クラス SVMと2クラスSVMがある。
- 2クラスSVMには、ハードマージンSVMとソフトマージンSVMがある。
・回帰機能には下記がある。
- 線形SV回帰と非線形SV回帰がある。
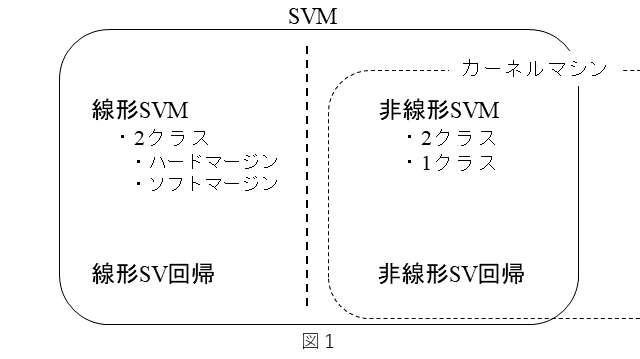
非線形SVMおよび非線形SV回帰は、カーネル関数を用いますので、カーネルマシンとして扱われることもあります。以上を図1にまとめてみました。
SVMを体系的に理解するには、次の順序で進めて行くのが良いのではないかと思います。
- 分類器としての2クラスハードマージン線形SVM
↓
- 分類器としての2クラスソフトマージン線形SVM
↓
- 分類器としての2クラス非線形SVM
↓
- 分類器としての1クラス非線形SVM
↓
- 回帰としての線形SV回帰/非線形SV回帰
今回は、「4. 分類器としての1クラス非線形SVM」について、おさらいします。特にその1形態であります1クラス$\nu$サポートベクトルマシンについておさらいします。
2. 2クラス非線形SVMを簡単におさらい
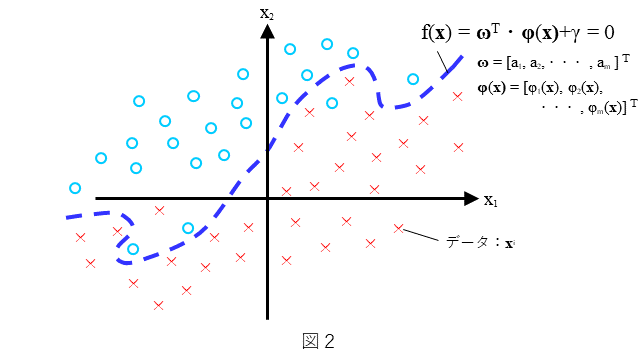
まず、2クラス非線形SVMを簡単におさらいしておきます。分類器としての2クラス非線形SVMは、どのような分類を考えるのか、を図2に示します。わかりやすいように2次元で表しています。(1)式で示される曲線 によりデータができるだけ(○と×に)2分可能なデータの分布を考えます。
$$
f({\bf x}),=,{\bf \omega}^T{\bf\phi}({\bf x}),+,\gamma = 0\hspace{1cm}・・・(1)
$$
ここに、${\bf\phi}(\bf{x})$ は、図中にもありますが(2)式で示されるように、非線形関数$\phi_k({\bf x})$ のベクトルで表されます。
$$
{\bf\phi}({\bf x})=[,\phi_1({\bf x}),,\phi_1({\bf x}),,\cdots,,\phi_m({\bf x}),]\hspace{1cm}・・・(2)
$$
すなわち、(1)式で表される曲線は、非線形関数 $\phi_k({\bf x})$ の線形結合です。ここで、データの分布は図2にありますように、ある曲線で全てのデータが分離することはできないような分布とします。できるだけ多くの${\bf x}$に対して、${\bf x}$ が○のときは $f({\bf x})>0$ となり、${\bf x}$ が×のときは$f({\bf x})<0$ となるような $f({\bf x})$ を求めること、すなわち、$\bf{\omega}$ と $\gamma$ を決めることを考えます。
2クラス非線形SVMの式を、2クラス線形SVM(ソフトマージン)の式から導出していきます。まず、2クラス(3)式は、2クラス線形SVM(ソフトマージン)の式です。
$$
f_l({\bf x})={\bf\omega}_l^{T}{\bf x} + \gamma_l=0\hspace{1cm}・・・(3)
$$
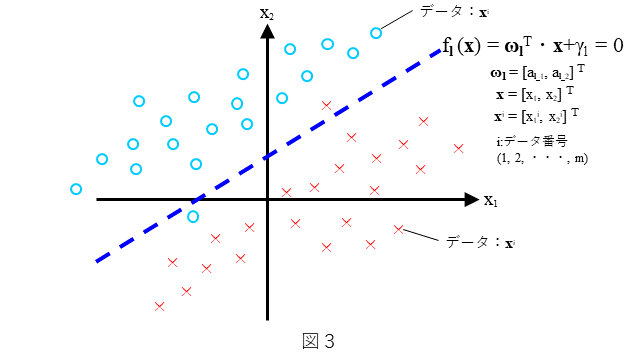
(3)式の意味を図化したものを図3に示します。わかりやすいように2次元で表しています。直線 $f_l({\bf x})={\bf\omega}_l^{T}{\bf x} + \gamma_l=0$ によりデータが、できるだけ(○と×に)2分可能なデータの分布を考えます。ここで、データの分布は図3にありますように直線で全てのデータが分離することはできないような分布とします(ソフトマージンは、このような分布を前提としています)。できるだけ多くの${\bf x}$に対して、${\bf x}$が○のときは$f_l({\bf x})>0$ となり、${\bf x}$が×のときは$f_l({\bf x})<0$ となるような $f_l({\bf x})$ を求めること、すなわち、${\bf\omega}_l$ と $\gamma_l$ を決めることを考えます。
上記の条件を満たすような直線を与える式を(4)式に示します。
$$
f_l({\bf x}),=,\sum{\alpha_l}^iy^i{{\bf x}^i}^T{\bf x},+,(,{y’}^i – \sum{\alpha_l}^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i,),=0\hspace{1cm}・・・(4)
$$
$$
{\bf\omega}_l=\sum{\alpha_l}^iy^i{\bf x}^i\hspace{1cm}・・・(5)
$$
$$
\gamma_l = {y’}^i – \sum{\alpha_l}^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i\hspace{1cm}・・・(6)
$$
ここに、${\alpha_l}^i$ は、ラグランジュの双対問題で定義される双対変数です。また、$\bf{x}'$および$y'$は、${\alpha_l}^i$の値が下記の条件を満たすときの定義される値です。
$$
\begin{array}{l}
,&{{\bf x}’}^i : 0 < {\alpha_l}^i < C,のときの,{\bf x}\
,&{y’}^i : 上記の{{\bf x}'}^iに対応した正解ラベル,y
\end{array}
$$
ここに、${\bf x}^i,,{{{\bf x}}'}^i$ は学習データであり、${\bf x}$ はテストデータであることに注意しましょう。(4)式において、${\bf x}$ → $\phi({\bf x}) $、${\bf x}^i$ → $\phi({\bf x}^i) $、${{\bf x}'}^i$ → $\phi({{\bf x}'}^i) $ と置き換えますと、(7)式が得られます。
$$
f({\bf x}),=,\sum\alpha^iy^i{\bf\phi}({{\bf x}^i})^T{\bf\phi}({\bf x}),+,(,{y’}^i – \sum\alpha^i{y}^i{\bf\phi}({{\bf x}^i})^T{\bf\phi}({{\bf x}'}^i),),=0\hspace{1cm}・・・(7)
$$
ここに、(8)式で定義される非線形関数の内積として表されますカーネル関数 $K({\bf a},{\bf b})$ を導入して(7)式に代入しますと、(9)式が得られます。
$$
K({\bf a},{\bf b})={\bf\phi}({\bf a})^T{\bf\phi}({\bf b})\hspace{1cm}・・・(8)
$$
$$
f({\bf x}),=,\sum\alpha^iy^iK({{\bf x}^i,, {\bf x}}),+,(,{y’}^i – \sum\alpha^i{y}^iK({{\bf x}^i},, {{{\bf x}'}^i}),)=0\hspace{1cm}・・・(9)
$$
(9)式が、非線形SVMの識別線(曲線)を与える式です。カーネル関数には、様々な形がありますが、代表的なカーネル関数を(10)式、(11式、(12)式に挙げておきます。
$$
\begin{array}{l}
,&ガウスカーネル\
,&Kc({\bf a},{\bf b}) = exp(,-\beta,||{\bf a},–,{\bf b}||^ 2,)\hspace{1cm}・・・(10)
\end{array}
$$
$$
\begin{array}{l}
,&多項式カーネル\
,&Km({\bf a},{\bf b}) = (,1 + {\bf a}^T・{\bf b},)^p\hspace{1cm}・・・(11)
\end{array}
$$
$$
\begin{array}{l}
,&シグモイドカーネル\
,&Ks({\bf a},{\bf b}) = tanh(,c,{\bf a}^T・{\bf b} + 1,)\hspace{1cm}・・・(12)
\end{array}
$$
ちなみに、(9)式においてカーネル関数を(10)式に示されますガウスカーネルとすると、(13)式に示す形となります。
$$
f({\bf x}),=,\sum\alpha^iy^i,exp(,-\beta,||{\bf x}^i,–,{\bf x}||^ 2,),+,(,{y’}^i – \sum\alpha^i{y}^i,exp(,-\beta,||{{\bf x}^i},–,{{{\bf x}'}^i}||^ 2,)=0\hspace{1cm}・・・(13)
$$
(1)式を見ますと、非線形SVMの曲線を表す式は、非線形関数 ${{\bf\phi}(\bf x)}$ の線形結合で表されています。(1)式で表される $f({\bf x})$ は、${\bf x}$ に対しては非線形ですが、 ${\bf\phi}({\bf x})$ に対しては線形です。つまり、 いわば ${\bf x}$ の空間では $f({\bf x})=0$ は曲線ですが、${\bf\phi}({\bf x})$ の空間では$f({\bf x})=0$ は直線(平面)であると言えます。その意味では、2クラス非線形SVMは、${\bf\phi}({\bf x})$ の空間上の2クラス線形SVMと言えます。
また、(9)式を見ますと、非線形SVMの曲線を表すにあたり、非線形関数 ${\bf \phi}({\bf x})$ を直接扱わなくなくて済んでます。「非線形SVMの式においては、非線形関数は内積の形でしか現れない」ということに着目し、「非線形関数の内積はカーネル関数という扱いやすい関数に置き換えられる」ということをうまく利用したことで、比較的簡便に非線形関数のパラメータを最適化できるようになっています。このような非線形SVM特有の性質をカーネルトリックと呼びます。
なお、ラグランジュの双対問題として解く手順を含めて、2クラス線形SVMおよび2クラス非線形SVMの詳細については、別記事で紹介しておりますので、ご参考頂ければと思います。
3. どのような分類を考えるのか?
1クラス非線形SVMは、1クラスの名称が指してますように、データのクラスは一つしかない状態を前提とします。前章で示しました図2もしくは図3に基づけば、○もしくは×のどちらかしかない状態を指します。1クラスのデータだけで分類を行うということは、得られている一つのクラスのデータだけでなんらかの領域を定義し、その領域内にあるデータとその領域外にあるデータで分類するというものです。
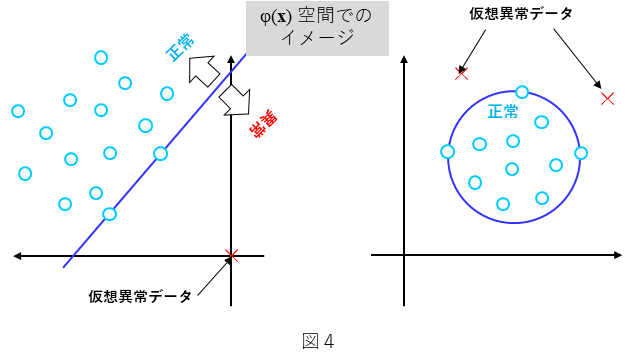
図4に1クラス非線形SVMの2つの代表的な形態を示します。ここで、○を正常データとし、×を仮想異常データとします。これは、一般に正常データを比較的、多量に収集することが可能ですが、その一方で、異常データは得られにくいことが多いことを想定しています。すなわち、○の正常データを用いた1クラス非線形SVMを考えます。図4の左側は、直線を境に○と×を分類するものです。一方、図4の右側は、円の内側と外側で○と×を分類するものです。なお、図4は、いずれもデータ $\bf x$ を非線形関数 $\phi({\bf x})$ で射像した空間における表現です。すなわち元空間であるデータ $\bf x$ の空間では、図4における直線も円も非線形な形となります。また、図4は、2次元で表していますが、3次元以上でも同様の考え方が適用されます。その場合は、直線は超平面であり、円は超球となります。次章で、直線(超平面)の場合の場合について、具体的に御説明します。
4. 1クラス非線形SVM:1クラス$\nu$サポートベクトルマシン
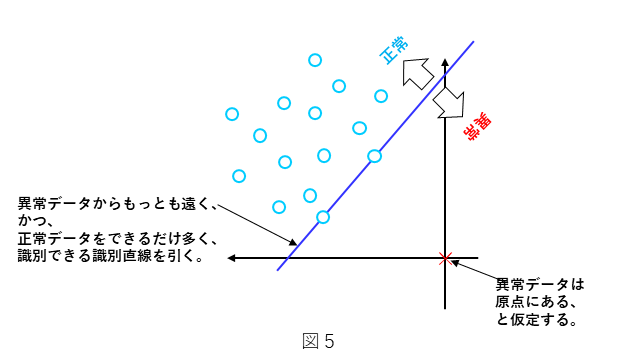
前章で示しました図4の左側にあたります識別直線を境に○と×を分類する1クラス非線形SVMである 1クラス$\nu$サポートベクトルマシンについて説明します。図5にその考え方を示します。○の正常データを用いた1クラス非線形SVMとします。図5に示しますように、$\nu$サポートベクトルマシンの場合、○の正常データは、識別直線より上側に分布し、×の仮想異常データは原点にあると仮定します。前章で述べましたように、図5はあくまでもデータ $\bf x$ を非線形関数 $\phi({\bf x})$ で射像した空間での表現ですので、○の正常データと×の異常データが図5のように分布するように非線形関数 $\phi({\bf x})$ を使って $\bf x$ を射像した結果と考えます。このとき、識別直線は、次のi)とii)の条件を満たすように決めるのが良さそうです。
i) 識別直線は、異常データ×からできるだけ遠ざかるようにする。
ii) 正常データ○は、できるだけ多く、識別直線の上側に存在するようにする。
この条件i)はできるだけ直線を原点から遠ざけることを意味し、条件ii)はできるだけ直線を原点に近づけることを意味しますので、両条件はトレードオフの関係にあります。
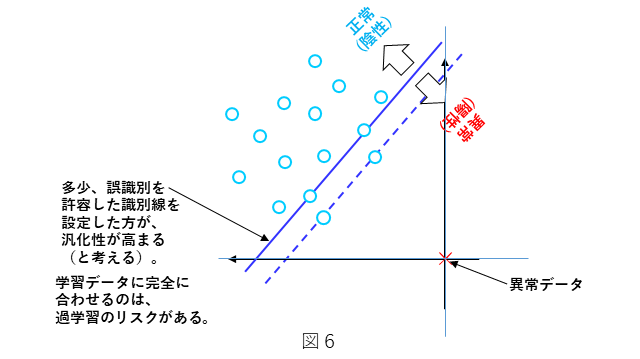
この考え方で直線を決めるということは、図6に示しますように、識別直線を原点(仮想異常データ)から遠ざけることで、異常の識別率を上げることを意味します。同時に、正常データに対して、誤識別を許容することを意味します。一方で、テスト時の正常データの分布は、学習データの正常データと完全に一致することは、まずないと考えて良いので、この考え方で直線を決めるということは、多少の誤識別を許容するような、ほどよいところに識別直線の位置を決めると、学習データに対する過学習を防止し、テストデータに対する汎化性を担保する側面もあります。
次に、この識別直線を数式で表すことを考えていきます。まずは、条件i)を満たす直線を決めるような条件を定式化し、さらに、ii)を満たすように所定の距離だけ、直線を原点(異常データ×)に近づける(戻す)ような条件を定式化します。
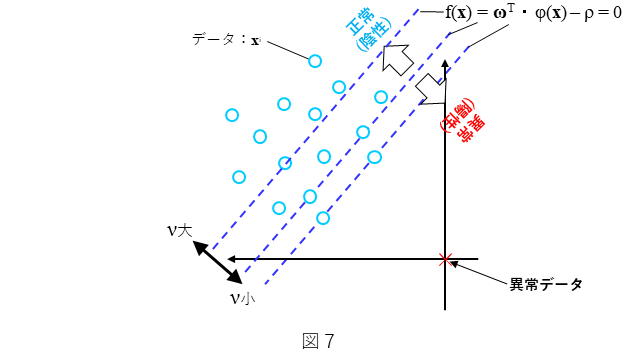
図7にも示しておりますように、 $\bf x$ を非線形関数 $\phi({\bf x})$ を使って射像した非線形空間上での識別直線 $f({\bf x})$ を(14)式のように置きます。なお、${\bf\phi}({\bf x})$ は、(2)式で定義されます。
$$
\begin{eqnarray}
,&f({\bf x})={\bf\omega}^T\cdot{\bf{\phi}}({\bf x}),-,\rho =0\hspace{1cm}・・・(14)\
,&(,\rho>0,)\
\end{eqnarray}
$$
(14)式より、原点(仮想異常データ)${\bf x}_0$ と識別直線の距離 $l$ は、(15)式で表されます。
$$
l=\frac{|,{\bf\omega}^T\cdot{{\bf\phi}({\bf x}_0)-\rho,}|}{||{\bf\omega}||}\hspace{1cm}・・・(15)
$$
ここで、${\bf x}_0 = [0,0,\cdots,0]$ かつ $\rho>0$ なので、(15)式に代入して、(16)式が得られます。
$$
l=\frac{\rho}{||{\bf\omega}||}\hspace{1cm}・・・(16)
$$
前述の条件i)を満たすということは、$l$ を大きくするということですので、(16)式から、$\rho$ → 大($-\rho$ → 小)、もしくは、$||\bf\omega||$ → 小が条件であることがわかります。以上から、(17)式で示される最適化の式を立てます。
$$
\underset{{\bf\omega,,\rho}}{min},\frac{1}{2}||{\bf\omega}||^2-\rho\hspace{1cm}・・・(17)
$$
$1/2||\omega||^2$ の項は、最適化しやすいように2次形式にしています。しかし、(17)式において、$1/2||{\bf\omega}||^2,-,\rho$ の値は、$\rho$ → 大($-\rho$ → 小)とすることで、いくらでも小さくすることができます。そこで、前述の条件ii)を追加することで、識別直線が無制限に原点(仮想異常データ)から遠ざかることを制限します。ここで、(18)式で定義されるパラメータ $\nu$ を導入します。
$$
\begin{eqnarray}
,&\frac{m_a}{M}\leq\nu\leq\frac{m_b}{M}\hspace{1cm}・・・(18)\
,&\
,& m_a:f({\bf x}_i)< 0となる正常データ数(識別直線より下の領域にある正常データ個数)
\
,& m_b:f({\bf x}_i)\leq 0となる正常データ数(識別直線より下の領域にある正常データ個数+識別線上にあるデータ個数)\
,& M:全正常データ数
\end{eqnarray}
$$
$m_a/M$ は、学習データにおける誤識別率(異常検知の文脈では偽陽性率)を意味しますので、$\nu$ は、ほぼ偽陽性率であることがわかります。このことから $\nu$ は図7で示されるように、その値が大きくなると原点(仮想異常データ×)から遠ざかり、その値が小さくなると原点(仮想異常データ×)に近づくようなパラメータとします。
これを踏まえて、(19)式で示される項を考えます。
$$
\frac{1}{M\nu}\sum max\{,0,,-(,{\bf\omega}^T\cdot{\bf\phi}({\bf x}^i)-\rho,),\}\hspace{1cm}・・・(19)
$$
学習データ ${\bf x}^i$ に対して異常と判定したとき、${\bf\omega}^T・{\bf \phi}({\bf x}^i),–,\rho<0$ となりますが、学習データ ${\bf x}^i$は正常データですので、誤識別したことになります。したがって、 (20)式において、$max\{0, -(\,{\bf\omega}^T・{\bf\phi}({\bf x}^i)\,–\,\rho\,)\}$ は、誤識別数と相関があり、 $\sum max\{0, -(\,{\bf\omega}^T・{\bf\phi}({\bf x}^i)\,–\,\rho\,)\}$ は、その総和を表します。また、$M\nu$ は、(18)式より、ほぼ誤識別したデータ数ですので、 $\sum max\{0, -(\,{\bf\omega}^T・{\bf\phi}({\bf x}^i)\,–\,\rho\,)\}$ を規格化した値と言えます。
前述しましたように、(17)式において、$1/2||{\bf\omega}||^2,-,\rho$ の値は、$\rho$ → 大($-\rho$ → 小)とすることで、いくらでも小さくすることができますが(識別直線をいくらでも原点から遠ざけることができますが)、このとき、(20)式の値は、逆に応分、大きくなることがわかります。そこで、識別直線をいくらでも原点から遠ざけられないように、(17)式に(19)式を追加して、(20)式とします。
$$
\underset{{\bf\omega,,\rho}}{min},\frac{1}{2}||{\bf\omega}||^2-\rho,+\frac{1}{M\nu}\sum max{,0,,-(,{\bf\omega}^T\cdot{\bf\phi}({\bf x}^i)-\rho,),}\hspace{1cm}・・・(20)
$$
これまでの説明から(20)式の第1項と第2項は、前述の条件i)に該当し、第3項は、前述の条件ii)に該当することがわかります。以上、1クラス$\nu$サポートベクトルマシンの定式化を示しました。
次に、(20)式を満たす $\bf\omega$ と $\rho$ を求める解法について説明します。別記事で紹介しておりますが、2クラス線形SVM、2クラス非線形SVMのいずれもラグランジュの双対問題に帰着します。1クラス$\nu$サポートベクトルマシンも同じく、ラグランジュの双対問題に帰着します。まずは、双対問題と対となる主問題を定義します。主問題は、2次計画問題の形とするのが一般的です。2次計画問題とは、目的関数が2次形式であり、制約条件が1次関数である最適化問題ですので、(20)式を(21)式および(22)式のような形に変形します。
$$
\underset{{\bf\omega,,\rho,,\xi}}{min},\frac{1}{2}||{\bf\omega}||^2-\rho,+\frac{1}{M\nu}\sum \xi^i\hspace{1cm}・・・(21)
$$
$$
s.t.,\xi^i\geq0,,\xi^i\geq-(,{\bf\omega}^T\cdot{\bf\phi}({\bf x}^i)-\rho,)\hspace{1cm}・・・(22)
$$
なお、(22)式の制約条件については、$\xi^i=max\{,0,,-(,{\bf\omega}^T\cdot{\bf\phi}({\bf x}^i)-\rho,),\}$ と置きますと、${\bf x}^i$(=正常データ)が正しく識別されたときは、$\xi^i=0$ であり、誤識別されたときは、${\bf\omega}^T・{\bf \phi}({\bf x}^i),–,\rho<0$ となりますので、$\xi^i\geq-(\,{\bf\omega}^T\cdot{\bf\phi}({\bf x}^i)-\rho\,)$ となります。(22)式で示される制約条件は、前述の条件ii)を意味していることになります。
次に、(21)式と(22)式で表される主問題に対応する双対問題を(23)式と(24)式に示します。
$$
\underset{\alpha^i,,\mu^i}{max},,\underset{{\bf\omega},,\rho,,\xi^i}{min};\frac{1}{2}||{\bf\omega}||^2-\rho+\frac{1}{M\nu}\sum{\xi^i}-\sum \alpha^i({\bf\omega}^T\cdot{\bf\phi}({\bf x}^i)-\rho+\xi^i,)-\sum\mu^i\xi^i\hspace{1cm}・・・(23)
$$
$$
s.t.;\alpha^i\geq0,;\mu^i\geq0\hspace{1cm}・・・(24)
$$
(23)式と(24)式で示される双対問題は、(25)式および(26)式に帰着します。
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^i{\alpha}^jK({\bf x}^i,{\bf x}^j)\hspace{1cm}・・・(25)
$$
$$
s.t.;0\leq{\alpha}^i\leq\frac{1}{M\nu},;;\sum\alpha^i=1\hspace{1cm}・・・(26)
$$
ここに、$K({\bf x}^i,{\bf x}^j)$ は、(8)式で定義されるカーネル関数です。そして、(26)式および(27)式を解くことで、識別直線の式を表す(27)式が得られます。
$$
f(x) = \sum\alpha^i K({\bf x}^i, {\bf x}) - \sum\alpha^i K({\bf x}^i, {\bf x'}^i) = 0\hspace{1cm}・・・(27)
$$
$$
{{\bf x}’}^i : 0 < \alpha^i < \frac{1}{M\nu},のときの,{\bf x}^i
$$
ここに、${\bf x}^i$ および ${{\bf x}'}^i$は学習データ、${\bf x}$ はテストデータです。(14)式は、(27)式として得られることになります。(27)式を見ますと、非線形関数 ${\bf \phi}({\bf x})$ を直接扱わなくなくて済んでます。「1クラス$\nu$サポートベクトルマシンの式においては、非線形関数は内積の形でしか現れない」ということに着目し、「非線形関数の内積はカーネル関数という扱いやすい関数に置き換えられる」ということをうまく利用したことで、比較的簡便に非線形関数のパラメータを最適化できるようになっています。このような性質をカーネルトリックと呼び、同じく非線形関数を用いる2クラス非線形SVMでもカーネルトリックが現れています。
以上、前章で示しました図4の左側にあたります識別直線を境に○と×を分類する1クラス非線形SVMである 1クラス$\nu$サポートベクトルマシンについて説明しました。なお、SVMのパラメータ最適化をラグランジュの双対問題として解く手順については、2クラスソフトマージン線形SVMの記事で紹介しておりますので、ご参考頂ければと思います。
5. おわりに
今回は、1クラス非線形SVMの1形態であります1クラス$\nu$サポートベクトルマシンと呼ばれるSVMについておさらいしました。1クラス$\nu$サポートベクトルマシンの定式化をできるだけわかりやすいアプローチで紹介したつもりです。1クラス$\nu$サポートベクトルマシンも2クラス非線形SVMと同じく、カーネルトリックを用いることで数学的に扱いやすくなっていること、また、2クラス線形SVMおよび2クラス非線形SVMと同じく、ラグランジュの双対問題を経て、1つの双対変数を最適化する問題に帰着する点が面白いと思って頂けた方もいらっしゃるのではないでしょうか。1クラス非線形SVMは、今回ご紹介しました1クラス$\nu$サポートベクトルマシンの他にサポートベクトル領域記述法があります。また、2クラスSVMとして、2クラス線形SVM、2クラス非線形SVMがあります。これらについては他の記事で紹介しますので、ご興味のある方はご参考下さい。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
竹内 一郎、鳥山昌幸:サポートベクトルマシン
赤穂昭太郎:カーネル多変量解析