こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、SVM(Support Vector Machine)をおさらいします。
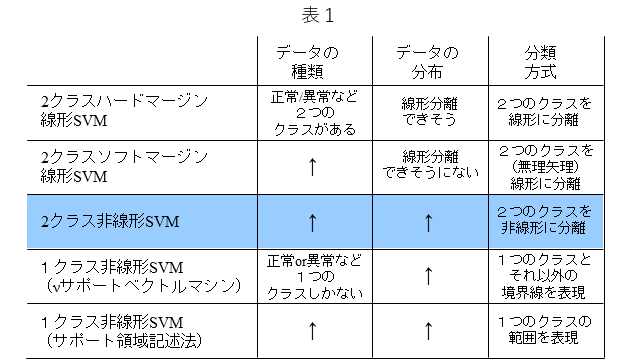
表1は、代表的なSVMをまとめています。SVMはクラス分類器ですが、データの種類、データの分布、分類方式に応じて、適切なSVMを選ぶことができます。また、SVMは、説明性に優れる一方で、ディープラーニングなどのカッティング・エッジな手法と比較しますとその精度は劣るというのが一般的な評価ではないかと思います。しかし、SVMは前記のように説明性に優れることに加え、その学習は、凸問題に帰着することから、大域最適解であることが保証されるなど、理論的には魅力的なところが多々あります。表中のSVMから、今回は、2クラス非線形SVMと呼ばれるSVMについておさらいします。
1. はじめに
SVMには、いくつかの種類があります。以下に簡単にまとめます。
・分類と回帰の機能がある。
・分類機能には下記がある。
- 線形SVMと非線形SVMがある。
- 1クラス SVMと2クラスSVMがある。
- 2クラスSVMには、ハードマージンSVMとソフトマージンSVMがある。
・回帰機能には下記がある。
- 線形SV回帰と非線形SV回帰がある。
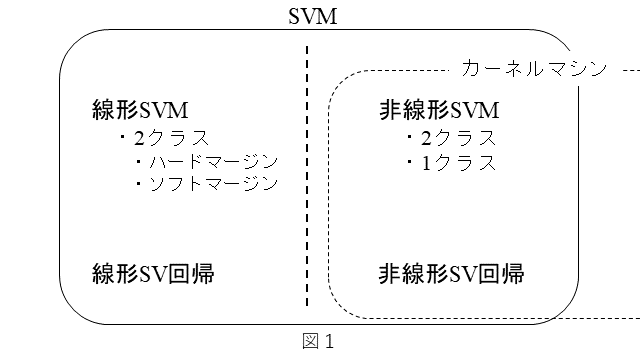
非線形SVMおよび非線形SV回帰は、カーネル関数を用いますので、カーネルマシンとして扱われることもあります。以上を図1にまとめてみました。
SVMを体系的に理解するには、次の順序で進めて行くのが良いのではないかと思います。
- 分類器としての2クラスハードマージン線形SVM
↓
- 分類器としての2クラスソフトマージン線形SVM
↓
- 分類器としての2クラス非線形SVM
↓
- 分類器としての1クラス非線形SVM
↓
- 回帰としての線形SV回帰/非線形SV回帰
今回は、「3. 分類器としての2クラス非線形SVM」について、おさらいします。
2. 2クラスソフトマージン線形SVMを簡単におさらい
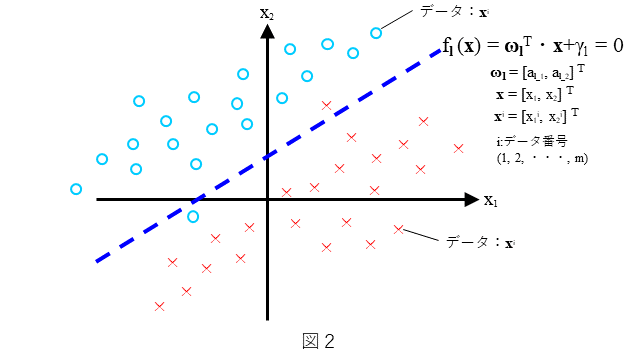
まず、2クラスソフトマージン線形SVMを簡単におさらいしておきます。分類器としての2クラスソフトマージン線形SVMは、どのような分類を考えるのか、を図2に示します。わかりやすいように2次元で表しています。直線 $f_l({\bf x})={\bf\omega}_l^{T}{\bf x} + \gamma_l=0$ によりデータが、できるだけ(○と×に)2分可能なデータの分布を考えます。ここで、データの分布は図2にありますように直線で全てのデータが分離することはできないような分布とします(ソフトマージンは、このような分布を前提としています)。できるだけ多くの${\bf x}$に対して、${\bf x}$が○のときは $f_l({\bf x})>0$ となり、${\bf x}$ が×のときは $f_l({\bf x})<0$ となるような $f_l({\bf x})$ を求めること、すなわち、${\bf\omega}_l$ と $\gamma_l$ を決めることを考えます。
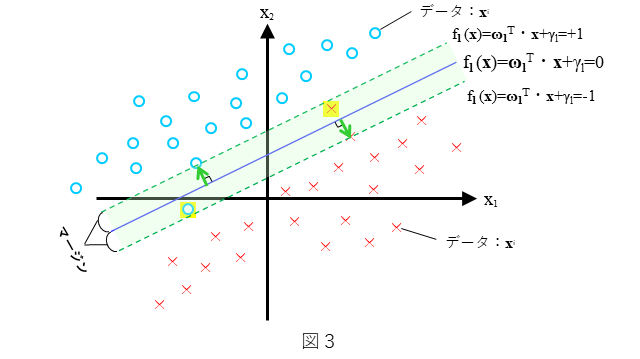
具体的には、図3で示されるような直線 $f_l({\bf x})=0$ に対するマージンを考え、そのマージンが最大化するような直線を考えます。マージンを最大化するような直線 $f_l({\bf x})=0$ とは、いくつかの○と× は正しく分離できていないことを許容しつつ、直線 $f_l({\bf x})=0$ からもっとも近い○と×それぞれから直線 $f_l({\bf x})=0$ に垂線を下ろしたとき、双方の垂線の長さが同時に最大となる(=等しくなる)ような直線 ${f_l({\bf x})=0}$ であり、このような直線は一意に決まります。このとき直線 ${f_l({\bf x})=0}$ をソフトマージン線形SVMと呼びます。
(1)式と(2)式は、上記の条件を満たす直線 $f_l({\bf x})={\bf\omega}_l^{T}{\bf x} + \gamma_l=0$ を求めるための条件です。
$$
\begin{eqnarray}
,&y^i\cdot({\bf \omega}_l^T{\bf x}^i+\gamma_l)\geq 1-{\xi_l}^i \hspace{1cm}・・・(1)\
,&;({\xi_l}^i\geq0)\
,&\
,&\underset{{\bf \omega}_l,;\gamma_l}{min};\frac{1}{2}||{\bf \omega}_l||^2+C\sum{\xi_l}^i\hspace{1cm}・・・(2)
\end{eqnarray}
$$
ここで、$y^i$ は、下式で表されるように、学習データ ${\bf x}^i$( $i$:データ番号 ) ひとつひとつに付与される正解ラベルです。
$$
y^i=\left\{
\begin{array}{ll}
,+1(,{\bf x}^iが○のとき,) \
,-1(,{\bf x}^iが×のとき,) \
\end{array}
\right.
$$
また、図3中に示されておりますように、上側のマージン直線は(3)式で表され、下側のマージン直線は(4)式で表されます。
$$
\begin{array}{l}
,&{\bf \omega_l}^T{\bf x}^i+\gamma_l=+1\hspace{1cm}・・・(3)\
,&{\bf \omega_l}^T{\bf x}^i+\gamma_l=-1\hspace{1cm}・・・(4)
\end{array}
$$
このとき(3)式で表されるマージン直線上もしくはそれより上側に全ての○が存在しているということを数式で表現すると、$y^i=1$ かつ $({\bf \omega}_l^T{\bf x}^i+\gamma_l)\geq 1$ なので、(5)式で表されます。また、(4)式で定義されるマージン直線上もしくはそれより下側に全ての×が存在しているということを数式で表現すると、×のデータを正しく分類できているときは、$y^i=-1$ かつ $({\bf \omega}_l^T{\bf x}^i+\gamma_l)\leq-1$ なので、○のときと同じく(5)式で表されます。
$$
y^i\cdot({\bf \omega}_l^T{\bf x}^i+\gamma_l)\geq 1 \hspace{1cm}・・・(5)
$$
これを踏まえて(1)式をあらためて見てみますと、(1)式の右辺は、$1-\xi^i,(\xi^i\geq0)$ ですので、$\xi^i>0$ のとき、(1)式の左辺は1より小さい値になり得ます。これは、$i$番目のデータが○ ($y^i=1$)であれば、(3)式で表されるマージン直線より下側に存在し得ることを意味し、あるいは、$i$番目のデータが×($y^i=-1$)であれば、(4)式で表されるマージン直線より上側に存在し得ることを意味します。すなわち、$\xi^i>0$ のとき、$i$番目のデータは正しく分類できていないことを意味します。なお、$\xi^i=0$ のときは、(1)式の左辺は、1以上の値になりますので、正しく分類されています(このとき、2クラスハードマージン線形SVMとなります)。このように、ソフトマージンにおける制約条件である(1)式は、いくつかの$x^i$に対して誤分類を許容するようになっています。
また、(6)式は、図3中のマージンが直線 $f({\bf x})=0$ からもっとも近い○と×それぞれから直線 $f({\bf x})=0$ に垂線を下ろしたとき、双方の垂線の長さが同時に最大となる(=等しくなる)ような○と×までの距離であることを意味しています(詳細は、ハードマージン線形SVMの編を参照)。
$$
\underset{{\bf \omega}_l,;\gamma_l}{min};||{\bf \omega}_l||^2\hspace{1cm}・・・(6)
$$
これを踏まえて(2)式をあらためて見てみますと、第1項の係数1/2は、微分に備えて便宜的に追加された係数であり、最小化にあたり影響を与えることはありません。第2項は、${\xi_l}^i$ の和に係数 $C$ が係っています。${\xi_l}^i$ は、上述しましたように、${\xi_l}^i>0$ のとき、$i$番目のデータは正しく分類できておらず、${\xi_l}^i$ の値が大きいほど、マージン直線に対して誤分類の領域に深く入っていくことを意味します。つまり、${\xi_l}^i$ の値が大きいほど、誤分類の程度が大きくなっていくと言えます。したがって、誤分類の程度が大きいほど、その総和である $\sum{\xi_l}^i$ は大きくなりますので、(1)式で示される制約条件でいくつかの$x^i$に対して誤分類を許容する一方で、(2)式の第二項で、無制限に誤分類を許容することを制約していると言えます。係数 $C$は、誤分類を許容させない程度を調節する係数と言えます。例えば、係数 $C$がの値が∞のとき、すべての ${\xi_l}^i$は、0でなければならなく、このときハードマージンとなります。逆に係数 $C$ の値が0のとき、すべての ${\xi_l}^i$は、$0\leq0\leq∞$ の任意の値を取ることが出来て、無制限に誤分類を許容することになります。
(1)式と(2)式の2つの式は、2次計画問題と言われる形をしています。2次計画問題とは、目的関数(ここでは(2)式)が2次形式であり、制約条件(ここでは(1)式)が1次関数である最適化問題です。2次計画問題には様々な解法がありますが、SVMの場合は、ラグランジュの双対問題として解くのが一般的です。ラグランジュの双対問題を解いて得られる解を(7)式と(8)式に示します。
$$
{\bf\omega}_l=\sum{\alpha_l}^iy^i{\bf x}^i\hspace{1cm}・・・(7)
$$
$$
\gamma_l = {y’}^i – \sum{\alpha_l}^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i\hspace{1cm}・・・(8)
$$
ここに、${\alpha_l}^i$ は、ラグランジュの双対問題で定義される双対変数です。また、${\bf{x}'}^i$および${y'}^i$は、${\alpha_l}^i$の値が下記の条件を満たすときの ${\bf x}^i$ および ${y}^i$ です。
$$
\begin{array}{l}
,&{{\bf x}’}^i : 0 < {\alpha_l}^i < C,のときの,{\bf x}\
,&{y’}^i : 上記の{{\bf x}'}^iに対応した正解ラベル,y
\end{array}
$$
SVMのパラメータ最適化をラグランジュの双対問題として解く手順については、2クラスソフトマージン線形SVMの記事で紹介しておりますので、ご参考頂ければと思います。
以上、2クラスソフトマージン線形SVMを表す直線 $f({\bf x})={\bf \omega}_l^T{\bf x}+\gamma_l = 0$ を求めるための条件である(1)式と(2)式について、簡単に説明しました。上述しましたように、いくつかの ${\bf x}^i$ に対して誤分類を許容しつつ、それ以外のデータ ${\bf x}^i $ は2つのマージン直線上もしくはそれより(いわば)外側に存在するようにマージン直線および直線 $f({\bf x})=0$ は決められます。したがって、テストデータを適用したときは、$f_l(\bf x)\geq1$ のとき、そのテストデータは○に分類されと判断し、$f_l({\bf x})\leq-1$ のとき、そのテストデータは、×に分類されたと判断することになります。2つのマージン直線に挟まれた領域に相当する $-1<f_l({\bf x})<1$ のときは、学習時には、正しく分類されたデータが存在しない領域ですので、テストデータの結果がこの領域に分類されたときは、本来はグレーゾーンです。2クラスソフトマージン線形SVMの詳細については、別記事で紹介しておりますので、ご参考頂ければと思います。
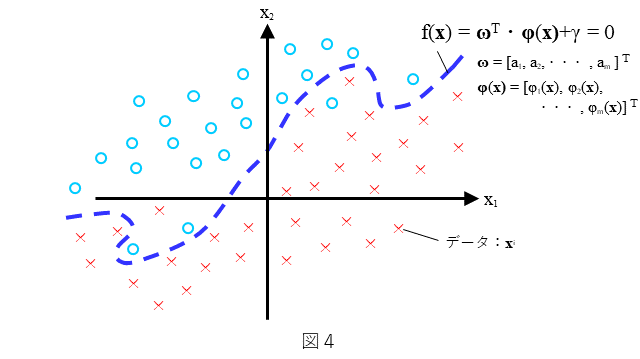
3. どのような分類を考えるのか?
分類器としての2クラス非線形SVMは、どのような分類を考えるのか、を図4に示します。わかりやすいように2次元で表しています。(9)式で示される曲線 によりデータができるだけ(○と×に)2分可能なデータの分布を考えます。
$$
f({\bf x}),=,{\bf \omega}^T{\bf\phi}({\bf x}),+,\gamma = 0\hspace{1cm}・・・(9)
$$
ここに、${\bf\phi}(\bf{x})$ は、図中にもありますが(10)式で示されるように、非線形関数$\phi_k({\bf x})$ のベクトルで表されます。
$$
{\bf\phi}({\bf x})=[,\phi_1({\bf x}),,\phi_1({\bf x}),,\cdots,,\phi_m({\bf x}),]\hspace{1cm}・・・(10)
$$
すなわち、(9)式で表される曲線は、非線形関数 $\phi_k({\bf x})$ の線形結合です。ここで、データの分布は図4にありますようにある曲線で全てのデータが分離することはできないような分布とします。できるだけ多くの${\bf x}$に対して、${\bf x}$ が○のときは $f({\bf x})>0$ となり、${\bf x}$ が×のときは$f({\bf x})<0$ となるような $f({\bf x})$ を求めること、すなわち、$\bf{\omega}$ と $\gamma$ を決めることを考えます。以上から、2クラス非線形SVMは、2クラスソフトマージン線形SVMの非線形版と言えます。
4. 定式化:線形SVMから非線形SVMへ
4.1 内積の形に着目
2章で示しました(7)式で与えられる ${\bf\omega}_l$ と $\gamma_l$ が非線形SVMでは線形SVMに対して、それぞれどのように変わるのか、という観点で説明していきます。(7)式と(8)式から、ソフトマージン線形SVMの直線 $f_l({\bf x}) = {\bf\omega}_l^T{\bf x},+,\gamma_l,=,0$ は、(11)式となります。
$$
f_l({\bf x}),=,\sum{\alpha_l}^iy^i{{\bf x}^i}^T{\bf x},+,(,{y’}^i – \sum{\alpha_l}^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i,),=0\hspace{1cm}・・・(11)
$$
ここに、${\bf x}^i,,{{{\bf x}}'}^i$ は学習データであり、${\bf x}$ はテストデータであることに注意しましょう。(11)式の第1項を見てみますと、${\bf x}^i$ と ${\bf x}$ の内積の形である ${{\bf x}^i}^T{\bf x}$ が含まれていることがわかります。また、第2項を見てみますと、${\bf x}^i$ と ${\bf x}'$ の内積の形である ${{\bf x}^i}^T{\bf x}'$ が含まれていることがわかります。この内積の形に着目します。非線形SVMを表す(9)式と線形SVMを表す(11)式を見比べてみて、${\bf x}$ → $\phi({\bf x}) $、${\bf x}^i$ → $\phi({\bf x}^i) $、${{\bf x}'}^i$ → $\phi({{\bf x}'}^i) $ と置き換えますと、(12)式が得られます。なお、パラメータである ${\alpha_l}^i$ も線形SVMのときから値が変わりますので、$\alpha^i$ と表記を変えています。
$$
f({\bf x}),=,\sum\alpha^iy^i{\bf\phi}({{\bf x}^i})^T{\bf\phi}({\bf x}),+,(,{y’}^i – \sum\alpha^i{y}^i{\bf\phi}({{\bf x}^i})^T{\bf\phi}({{\bf x}'}^i),),=0\hspace{1cm}・・・(12)
$$
(12)式において、非線形関数 $\phi_k({\bf x})$ が具体的にどのような形をしているかが、わかっているかあるいは決めることができれば、図4で示したような○と×に分類可能な曲線が得られたことになります。しかし、非線形関数 $\phi_k({\bf x})$ を具体的に決めるのは一般に困難です。そこでカーネル関数と呼ばれる関数を導入します。
4.2 カーネル関数(非線形関数の内積)
カーネル関数とは、(13)式で定義されるように、非線形関数の内積と等価な関数です。
$$
K({\bf a},{\bf b})={\bf\phi}({\bf a})^T{\bf\phi}({\bf b})\hspace{1cm}・・・(13)
$$
カーネル関数には、様々な形がありますが、代表的なカーネル関数を下記に挙げておきます。
$$
\begin{array}{l}
,&ガウスカーネル\
,&Kc({\bf a},{\bf b}) = exp(,-\beta,||{\bf a},–,{\bf b}||^ 2,)\hspace{1cm}・・・(14)
\end{array}
$$
$$
\begin{array}{l}
,&多項式カーネル\
,&Km({\bf a},{\bf b}) = (,1 + {\bf a}^T・{\bf b},)^p\hspace{1cm}・・・(15)
\end{array}
$$
$$
\begin{array}{l}
,&シグモイドカーネル\
,&Ks({\bf a},{\bf b}) = tanh(,c,{\bf a}^T・{\bf b} + 1,)\hspace{1cm}・・・(16)
\end{array}
$$
ここに、(14)式中の $\beta$、(15)式中の $p$、(16)式中の $c$ は、それぞれハイパーパラメータで、いわば曲線の曲げ度合い(曲線の表現力)を決めるパラメータです。(13)式から、${\bf\phi}({{\bf x}^i})^T{\bf\phi}({\bf x})$ → $K({{\bf x}^i,, {\bf x}})$ 、${\bf\phi}({{\bf x}^i})^T{\bf\phi}({{{\bf x}'}^i}) → K({{\bf x}^i},, {{{\bf x}'}^i})$ とそれぞれ置き換えて、(12)式に代入しますと、(17)式が得られます。
$$
f({\bf x}),=,\sum\alpha^iy^iK({{\bf x}^i,, {\bf x}}),+,(,{y’}^i – \sum\alpha^i{y}^iK({{\bf x}^i},, {{{\bf x}'}^i}),)=0\hspace{1cm}・・・(17)
$$
(17)式が、非線形SVMの分類曲線(識別曲線)を表しています。非線形SVMとは、線形SVMにおける学習データ ${\bf x}^i$ とテストデータ ${\bf x}$ の内積もしくは学習データ ${\bf x}^i$ と 学習データ ${{{\bf x}}'}^i$ の内積を、非線形関数の内積であるカーネル関数に置き換えたものであるとも言えます。ちなみに、(17)式においてカーネル関数をガウスカーネルとすると、(18)式に示す形となります。
$$
f({\bf x}),=,\sum\alpha^iy^i,exp(,-\beta,||{\bf x}^i,–,{\bf x}||^ 2,),+,(,{y’}^i – \sum\alpha^i{y}^i,exp(,-\beta,||{{\bf x}^i},–,{{{\bf x}'}^i}||^ 2,)=0\hspace{1cm}・・・(18)
$$
4.3 非線形SVMのラグランジュの双対問題
前節で示しました(17)式において、$\alpha^i$ の値は、線形SVMと同様にラグランジュの双対問題を解くことで得られます。ここでは、ラグランジュの双対問題の定式化に線形SVMと非線形SVMでどのような違いがあるかを説明しておきます。(19)式および(20)式は、2クラスソフトマージン線形SVMにおける ${\alpha_l}^i$ を求めるための最適化問題を定式化したものです。2クラスソフトマージン線形SVMの詳細については、別記事で紹介しておりますので、ご参考頂ければと思います。
$$
\underset{{\alpha_l}^i}{max},-\frac{1}{2}\sum{\alpha_l}^iy^i{{\bf x}^i}^T,\sum{\alpha_l}^jy^j{\bf x}^j,+,\sum{\alpha_l}^i\hspace{1cm}・・・(19)
$$
$$
s.t.;{\alpha_l}^i\geq0,;\sum{\alpha_l}^iy^i=0,;C-{\alpha_l}^i={\mu_l}^i\geq0\hspace{1cm}・・・(20)
$$
ここに、${\mu_l}^i$ は、${\alpha_l}^i$ と同じく、ラグランジュの双対問題で定義される双対変数です。(19)式および(20)式から、2クラスソフトマージン線形SVMは制約を考慮した凸問題に帰着していることがわかります。この(19)式と(20)式が、非線形SVMではどのように変わるかを考えていきましょう。まず、(19)式を(21)式のように変形します。
$$
\underset{{\alpha_l}^i}{max},-\frac{1}{2}\sum\sum{\alpha_l}^iy^i{\alpha_l}^jy^j{{\bf x}^i}^T{\bf x}^j,+,\sum{\alpha_l}^i\hspace{1cm}・・・(21)
$$
(21)式のように変形しますと、内積の形が見えてきます。ここで、${{\bf x}^i}^T{\bf x}^j$ → ${\bf \phi}({\bf x}^i)^T{\bf \phi}({\bf x}^j)^T$ → $K({\bf x}^i,{\bf x}^j)$ と置き換えますと、(22)式が得られます。
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^iy^i{\alpha}^jy^jK({\bf x}^i,{\bf x}^j),+,\sum{\alpha}^i\hspace{1cm}・・・(22)
$$
また、2クラスソフトマージン線形SVMは制約条件である(20)式は、2クラス非線形SVMでは(23)式のようになりますが、(20)式には、非線形の項(カーネル関数)が含まれないので、(20)式と(23)式は同じです。
$$
s.t.;{\alpha}^i\geq0,;\sum{\alpha}^iy^i=0,;C-{\alpha}^i={\mu}^i\geq0\hspace{1cm}・・・(23)
$$
(22)式は双対変数のうち $\alpha^i$ ( $\alpha^j$ )だけの関数で、(23)式の制約を考慮した凸問題に帰着したことがわかります。ちなみに、(22)式においてカーネル関数をガウスカーネルとすると、(24)式に示す形となります。
$$
\underset{{\alpha}^i}{max},-\frac{1}{2}\sum\sum{\alpha}^iy^i{\alpha}^jy^jexp(,-\beta,||{\bf x}^i,–,{\bf x}^j||^ 2,),+,\sum{\alpha}^i\hspace{1cm}・・・(24)
$$
(22)式と(23)式からなる制約付き最適化問題を解くことで $\alpha^i$ を得て、(17)式で定義される非線形SVMの分類曲線(識別曲線)が得られます。
4.4 カーネルトリック
$\alpha^i$ を求めるための最適化の式である(21)式あるいは(23)式を見ますと、非線形関数 ${\bf \phi}({\bf x})$ を直接扱わなくなくて済んでます。「非線形SVMの式においては、非線形関数は内積の形でしか現れない」ということに着目し、「非線形関数の内積はカーネル関数という扱いやすい関数に置き換えられる」ということをうまく利用したことで、比較的簡便に非線形関数のパラメータを最適化できるようになっています。このような非線形SVM特有の性質をカーネルトリックと呼びます。より具体的には、例えば、線形SVMの最適化の式である(20)式とカーネル関数としてガウスカーネルを用いた場合の非線形SVMの最適化の式である(23)式を見比べてみますと、(20)式では ${{\bf x}^i}^T{\bf x}^j$ の演算が、(23)式では $exp(,-\beta,||{\bf x}^i,–,{\bf x}^j||^ 2,)$ の演算に置き換わっています。$\beta$ を別途調整する必要はありますが、$exp(,-\beta,||{\bf x}^i,–,{\bf x}^j||^ 2,)$ の計算に特段の困難さはないと言えます。
5. おわりに
今回は、非線形SVMと呼ばれるSVMについておさらいしました。非線形SVMの定式化をできるだけわかりやすいアプローチで紹介したつもりです。非線形SVMは、線形SVM(特にソフトマージン線形SVM)が理解できていると、比較的容易に理解できるのではないでしょうか。特に非線形SVMは、カーネルトリック呼ばれるいわば仕掛けのようなものを使っているところが面白いと思って頂けた方もいらっしゃるのではないでしょうか。SVMは、今回ご紹介しました2クラス非線形SVMの他に、2クラスハードマージン線形SVM、2クラスソフトマージン線形SVM、1クラス非線形SVMなど、様々な形があります。これらについては他の記事で紹介しますので、ご興味のある方はご参考下さい。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
竹内 一郎、鳥山昌幸:サポートベクトルマシン
赤穂昭太郎:カーネル多変量解析