こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、SVM(Support Vector Machine)をおさらいします。
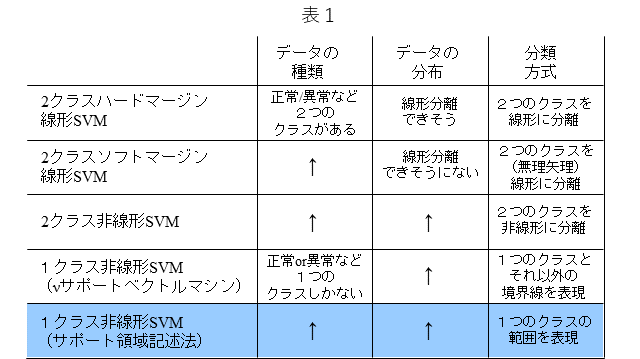
表1は、代表的なSVMをまとめています。SVMはクラス分類器ですが、データの種類、データの分布、分類方式に応じて、適切なSVMを選ぶことができます。また、SVMは、説明性に優れる一方で、ディープラーニングなどのカッティング・エッジな手法と比較しますとその精度は劣るというのが一般的な評価ではないかと思います。しかし、SVMは前記のように説明性に優れることに加え、その学習は、凸問題に帰着することから、大域最適解であることが保証されるなど、理論的には魅力的なところが多々あります。凸最適化問題は、局所解と大域最適解が同一である解空間での最適化問題で、局所解が複数存在するような最適化問題より容易に最適化が可能です。表中のSVMから、今回は、1クラス非線形SVMの中のサポートベクトル領域記述法と呼ばれるSVMについておさらいします。
1. はじめに
SVMには、いくつかの種類があります。以下に簡単にまとめます。
・分類と回帰の機能がある。
・分類機能には下記がある。
- 線形SVMと非線形SVMがある。
- 1クラス SVMと2クラスSVMがある。
- 2クラスSVMには、ハードマージンSVMとソフトマージンSVMがある。
・回帰機能には下記がある。
- 線形SV回帰と非線形SV回帰がある。
非線形SVMおよび非線形SV回帰は、カーネル関数を用いますので、カーネルマシンとして扱われることもあります。以上を図1にまとめてみました。
SVMを体系的に理解するには、次の順序で進めて行くのが良いのではないかと思います。
- 分類器としての2クラスハードマージン線形SVM
↓
- 分類器としての2クラスソフトマージン線形SVM
↓
- 分類器としての2クラス非線形SVM
↓
- 分類器としての1クラス非線形SVM
↓
- 回帰としての線形SV回帰/非線形SV回帰
今回は、「4. 分類器としての1クラス非線形SVM」について、おさらいします。特にその1形態でありますサポートベクトル領域記述法についておさらいします。
2. 2クラス非線形SVMを簡単におさらい
まず、2クラス非線形SVMを簡単におさらいしておきます。分類器としての2クラス非線形SVMは、どのような分類を考えるのか、を図2に示します。わかりやすいように2次元で表しています。(1)式で示される曲線 によりデータができるだけ(○と×に)2分可能なデータの分布を考えます。
$$
f({\bf x}),=,{\bf \omega}^T{\bf\phi}({\bf x}),+,\gamma = 0\hspace{1cm}・・・(1)
$$
ここに、${\bf\phi}(\bf{x})$ は、図中にもありますが(2)式で示されるように、非線形関数$\phi_k({\bf x})$ のベクトルで表されます。
$$
{\bf\phi}({\bf x})=[,\phi_1({\bf x}),,\phi_1({\bf x}),,\cdots,,\phi_m({\bf x}),]\hspace{1cm}・・・(2)
$$
すなわち、(1)式で表される曲線は、非線形関数 $\phi_k({\bf x})$ の線形結合です。ここで、データの分布は図2にありますようにある曲線で全てのデータが分離することはできないような分布とします。できるだけ多くの${\bf x}$に対して、${\bf x}$ が○のときは $f({\bf x})>0$ となり、${\bf x}$ が×のときは$f({\bf x})<0$ となるような $f({\bf x})$ を求めること、すなわち、$\bf{\omega}$ と $\gamma$ を決めることを考えます。
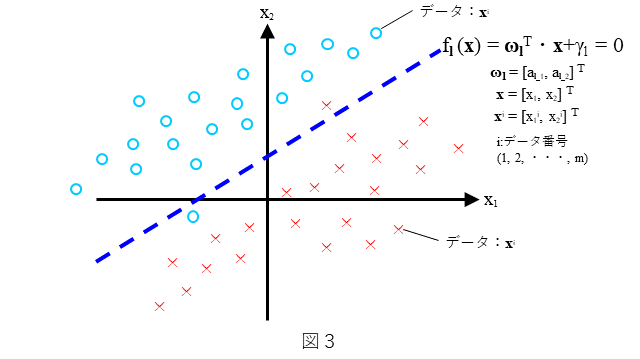
2クラス非線形SVMの式を、2クラス線形SVM(ソフトマージン)の式から導出していきます。まず、2クラス(3)式は、2クラス線形SVM(ソフトマージン)の式です。
$$
f_l({\bf x})={\bf\omega}_l^{T}{\bf x} + \gamma_l=0\hspace{1cm}・・・(3)
$$
(3)式の意味を図化したものを図3に示します。わかりやすいように2次元で表しています。直線 $f_l({\bf x})={\bf\omega}_l^{T}{\bf x} + \gamma_l=0$ によりデータが、できるだけ(○と×に)2分可能なデータの分布を考えます。ここで、データの分布は図3にありますように直線で全てのデータが分離することはできないような分布とします(ソフトマージンは、このような分布を前提としています)。できるだけ多くの${\bf x}$に対して、${\bf x}$が○のときは$f_l({\bf x})>0$ となり、${\bf x}$が×のときは$f_l({\bf x})<0$ となるような $f_l({\bf x})$ を求めること、すなわち、${\bf\omega}_l$ と $\gamma_l$ を決めることを考えます。
上記の条件を満たすような直線を与える式を(4)式に示します。
$$
f_l({\bf x}),=,\sum{\alpha_l}^iy^i{{\bf x}^i}^T{\bf x},+,(,{y’}^i – \sum{\alpha_l}^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i,),=0\hspace{1cm}・・・(4)
$$
$$
{\bf\omega}_l=\sum{\alpha_l}^iy^i{\bf x}^i\hspace{1cm}・・・(5)
$$
$$
\gamma_l = {y’}^i – \sum{\alpha_l}^i{y}^i{{\bf x}^i}^T{{\bf x}'}^i\hspace{1cm}・・・(6)
$$
ここに、${\alpha_l}^i$ は、ラグランジュの双対問題で定義される双対変数です。また、$\bf{x}'$および$y'$は、${\alpha_l}^i$の値が下記の条件を満たすときの定義される値です。
$$
\begin{array}{l}
,&{{\bf x}’}^i : 0 < {\alpha_l}^i < C,のときの,{\bf x}\
,&{y’}^i : 上記の{{\bf x}'}^iに対応した正解ラベル,y
\end{array}
$$
ここに、${\bf x}^i,,{{{\bf x}}'}^i$ は学習データであり、${\bf x}$ はテストデータであることに注意しましょう。(4)式において、${\bf x}$ → $\phi({\bf x}) $、${\bf x}^i$ → $\phi({\bf x}^i) $、${{\bf x}'}^i$ → $\phi({{\bf x}'}^i) $ と置き換えますと、(7)式が得られます。
$$
f({\bf x}),=,\sum\alpha^iy^i{\bf\phi}({{\bf x}^i})^T{\bf\phi}({\bf x}),+,(,{y’}^i – \sum\alpha^i{y}^i{\bf\phi}({{\bf x}^i})^T{\bf\phi}({{\bf x}'}^i),),=0\hspace{1cm}・・・(7)
$$
ここに、(8)式で定義される非線形関数の内積として表されますカーネル関数 $K({\bf a},{\bf b})$ を導入して(7)式に代入しますと、(9)式が得られます。
$$
K({\bf a},{\bf b})={\bf\phi}({\bf a})^T{\bf\phi}({\bf b})\hspace{1cm}・・・(8)
$$
$$
f({\bf x}),=,\sum\alpha^iy^iK({{\bf x}^i,, {\bf x}}),+,(,{y’}^i – \sum\alpha^i{y}^iK({{\bf x}^i},, {{{\bf x}'}^i}),)=0\hspace{1cm}・・・(9)
$$
(9)式が、非線形SVMの識別線(曲線)を与える式です。カーネル関数には、様々な形がありますが、代表的なカーネル関数を(10)式、(11式、(12)式に挙げておきます。
$$
\begin{array}{l}
,&ガウスカーネル\
,&Kc({\bf a},{\bf b}) = exp(,-\beta,||{\bf a},–,{\bf b}||^ 2,)\hspace{1cm}・・・(10)
\end{array}
$$
$$
\begin{array}{l}
,&多項式カーネル\
,&Km({\bf a},{\bf b}) = (,1 + {\bf a}^T・{\bf b},)^p\hspace{1cm}・・・(11)
\end{array}
$$
$$
\begin{array}{l}
,&シグモイドカーネル\
,&Ks({\bf a},{\bf b}) = tanh(,c,{\bf a}^T・{\bf b} + 1,)\hspace{1cm}・・・(12)
\end{array}
$$
ちなみに、(9)式においてカーネル関数を(10)式に示されますガウスカーネルとすると、(13)式に示す形となります。
$$
f({\bf x}),=,\sum\alpha^iy^i,exp(,-\beta,||{\bf x}^i,–,{\bf x}||^ 2,),+,(,{y’}^i – \sum\alpha^i{y}^i,exp(,-\beta,||{{\bf x}^i},–,{{{\bf x}'}^i}||^ 2,)=0\hspace{1cm}・・・(13)
$$
(1)式を見ますと、非線形SVMの曲線を表す式は、非線形関数 ${{\bf\phi}(\bf x)}$ の線形結合で表されています。(1)式で表される $f({\bf x})$ は、${\bf x}$ に対しては非線形ですが、 ${\bf\phi}({\bf x})$ に対しては線形です。つまり、 いわば ${\bf x}$ の空間では $f({\bf x})=0$ は、曲線ですが、${\bf\phi}({\bf x})$ の空間では $f({\bf x})=0$ は直線(平面)であると言えます。その意味では、2クラス非線形SVMは、${\bf\phi}({\bf x})$ の空間上の2クラス線形SVMと言えます。
また、(9)式を見ますと、非線形SVMの曲線を表すにあたり、非線形関数 ${\bf \phi}({\bf x})$ を直接扱わなくなくて済んでます。「非線形SVMの式においては、非線形関数は内積の形でしか現れない」ということに着目し、「非線形関数の内積はカーネル関数という扱いやすい関数に置き換えられる」ということをうまく利用したことで、比較的簡便に非線形関数のパラメータを最適化できるようになっています。このような非線形SVM特有の性質をカーネルトリックと呼びます。
なお、ラグランジュの双対問題として解く手順を含めて、2クラス線形SVMおよび2クラス非線形SVMの詳細については、別記事で紹介しておりますので、ご参考頂ければと思います。
3. どのような分類を考えるのか?
1クラス非線形SVMは、1クラスの名称が指してますように、データのクラスは一つしかない状態を前提とします。前章で示しました図2もしくは図3に基づけば、○もしくは×のどちらかしかない状態を指します。1クラスのデータだけで分類を行うということは、得られている1つのクラスのデータだけでなんらかの領域を定義し、その領域内にあるデータとその領域外にあるデータで分類するというものです。
図4に1クラス非線形SVMの2つの代表的な形態を示します。ここで、○を正常データとし、×を仮想異常データとします。これは、一般に正常データを比較的、多量に収集することが可能ですが、その一方で、異常データは得られにくいことが多いことを想定しています。すなわち、○の正常データを用いた1クラス非線形SVMを考えます。図4の左側は、直線を境に○と×を分類するものです。一方、図4の右側は、円の内側と外側で○と×を分類するものです。なお、図4は、いずれもデータ $\bf x$ を非線形関数 $\phi({\bf x})$ で射像した空間における表現です。すなわち元空間であるデータ $\bf x$ の空間では、図4における直線も円も非線形な形となります。また、図4は、2次元で表していますが、3次元以上でも同様の考え方が適用されます。その場合は、直線は超平面であり、円は超球となります。次章で、円(超球)の場合について、具体的に御説明します。
4. 1クラス非線形SVM:サポートベクトル領域記述法
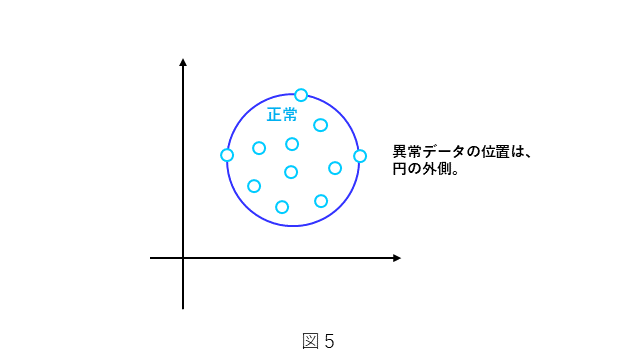
前章で示しました図4の右側にあたります円の内側と外側で○と×を分類1クラス非線形SVMであるサポートベクトル領域記述法について説明します。図5にその考え方を示します。○の正常データを用いた1クラス非線形SVMとします。図5に示しますように、サポートベクトル領域記述法の場合、○の正常データは、円周上もしくは円の内側に分布し、×の仮想異常データは円の外側にあると仮定します。前章で述べましたように、図5はあくまでもデータ $\bf x$ を非線形関数 $\phi({\bf x})$ で射像した空間での表現ですので、○の正常データと×の異常データが図5のように分布するように非線形関数 $\phi({\bf x})$ を使って $\bf x$ を射像した結果と考えます。このとき、円(中心と半径)は、次のi)とii)の条件を満たすように決めるのが良さそうです。
i) 円周は、異常データ×からできるだけ遠ざかるようにする。
ii) 正常データ○は、できるだけ多く、円の内側に存在するようにする。
この条件i)はできるだけ円の半径をできるだけ小さくすることを意味し、条件ii)はできるだけ円の半径をできるだけ大きくすることを意味しますので、両条件はトレードオフの関係にあります。
この考え方で円を決めるということは、円周を仮想異常データから遠ざけることで(正常範囲である円の大きさを小さくすることで)、異常の識別率を上げることを意味します。同時に、正常データに対して、誤識別を許容することを意味します。一方で、テスト時の正常データの分布は、学習データの正常データと完全に一致することは、まずないと考えて良いので、この考え方で円を決めるということは、多少の誤識別を許容するような、ほどよいところに円の大きさを決めると、学習データに対する過学習を防止し、テストデータに対する汎化性を担保する側面もあります。
次に、条件i)と条件ii)を満たす円を数式で表すことを考えます。まずは、条件i)を満たす円を決めるような条件を定式化し、さらに、ii)を満たすように所定の大きさだけ、円周を仮想異常データに近づける(戻す)ような条件を定式化します。
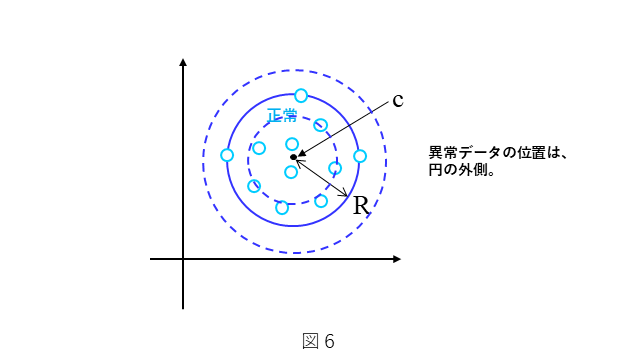
図6にも示しておりますように、 $\bf x$ を非線形関数 $\phi({\bf x})$ を使って射像した非線形空間上での円(球) の中心を $\bf c$ 、半径を $R$ とおきます。なお、${\bf\phi}({\bf x})$ は、(2)式で定義されます。
前述の条件i)を満たすということは、半径 $R$ をできるだけ小さくするということですので、(14)式を満たせば良いことになります。
$$
\underset{R^2}{min},R^2\hspace{1cm}・・・(14)
$$
(14)式は、明らかに、$R=0$ が解です。このとき、正常空間の大きさ(広さ)は0であり、前述の条件i)をもっとも満たしたことになります。
次に、条件ii)を満たすということは、半径 $R$ をできるだけ大きくするということですので、(15)式で示される値を考えます。
$$
r_{R^2}(||,{\bf\phi}({\bf x}^i)-{\bf c},||)\hspace{1cm}・・・(15)
$$
ここに、${\bf x}^i$は、学習データ(正常データ)であり、$i$ は、データ番号を指します。また、
$$
r_{R^2}(z)=max\{0,z-R^2\}\hspace{1cm}・・・(16)
$$
です。(15)式の値は、正常データの非線形射像である ${\bf\phi}({\bf x}^i$) が円の内側にあるとき、0になり、 ${\bf\phi}({\bf x}^i$) が円の外側にあるとき、円の中心から ${\bf\phi}({\bf x}^i$) までの距離の二乗である $||,{\bf\phi}({\bf x}^i)-{\bf c},||^2$ となります。したがって、(15)式を用いて、条件ii)を満たすことを定式化しますと、(17)式となります。
$$
\underset{R^2,,c}{min},\frac{1}{M}\sum r_{R^2}(||,{\bf\phi}({\bf x}^i)-{\bf c},||^2)\hspace{1cm}・・・(17)
$$
ここに、$M$ は、データ数です。$M$ で割ることで、データ数に依存しないようにしています。 (17)式は、明らかに、$R=$ ∞ が解です。このとき、正常空間の大きさ(広さ)は ∞ であり、前述の条件ii)をもっとも満たしたことになります。
以上、条件i)と条件ii)のトレードオフを定式化した(18)式を得ます。
$$
\underset{{R^2,,{\bf c}}}{min},,{\nu}R^2+\frac{1}{M}\sum r_{R^2}(||,{\bf\phi}({\bf x}^i)-{\bf c},||^2)\hspace{1cm}・・・(18)
$$
ここに、$\nu$ は、条件i)の強さを調節するパラメータです。$\nu$ を大きくするほど、円は大きくなりにくくなることがわかります。すなわち、$\nu$ が大きいほど、円は大きくなりにくくなりますので、正常データを異常と誤識別しやすくなることがわかります。このパラメータ $\nu$ は、もう一つの代表的な1クラスSVMであります1クラス$\nu$サポートベクトルマシンでも用いられていますが、同様の性質を持っています。なお、1クラス$\nu$サポートベクトルマシンの詳細につきましては、1クラス$\nu$サポートベクトルマシンの記事でご紹介しておりますので、ご参考頂ければと思います。
次に、(18)式を満たす $R^2$ と $\bf c$ を求める解法について説明します。別記事で紹介しておりますが、2クラス線形SVM、2クラス非線形SVM、1クラス$\nu$サポートベクトルマシンのいずれもラグランジュの双対問題に帰着します。サポートベクトル領域記述法も同じく、ラグランジュの双対問題に帰着します。まずは、双対問題と対となる主問題を定義します。主問題は、2次計画問題の形とするのが一般的です。2次計画問題とは、目的関数が2次形式であり、制約条件が1次関数である最適化問題ですので、(18)式を(19)式および(20)式のような形に変形します。
$$
\underset{{R^2,,{\bf c}}}{min},,{\nu}R^2+\frac{1}{M}\sum \xi^i\hspace{1cm}・・・(19)
$$
$$
s.t.,\xi^i\geq0,,\xi^i\geq ||,{\bf\phi}({\bf x}^i)-{\bf c},||^2-R^2\hspace{1cm}・・・(20)
$$
なお、(20)式の制約条件については、$\xi^i=max(,0,,r_{R^2}(||,{\bf\phi}({\bf x}^i)-{\bf c},||),)$ と置きますと、${\bf x}^i$(=正常データ)が正しく識別されたときは、$\xi^i=0$ であり、誤識別されたときは、$\xi^i\geq||,{\bf\phi}({\bf x}^i)-{\bf c},||^2-R^2>0$ となります。(20)式で示される制約条件は、前述の条件ii)を意味していることになります。
次に、(19)式と(20)式で表される主問題に対応する双対問題を(21)式と(22)式に示します。
$$
\underset{\alpha^i,,\mu^i}{max},,\underset{{R^2},,{\bf c},,\xi^i}{min};{\nu}R^2+\frac{1}{M}\sum \xi^i,-\sum\alpha^i(,\xi^i-||,{\bf\phi}({\bf x}^i)-{\bf c},||^2+R^2,)-\sum \mu^i\xi^i\hspace{1cm}・・・(21)
$$
$$
s.t.;\alpha^i\geq0,;\mu^i\geq0\hspace{1cm}・・・(22)
$$
(21)式と(22)式で示される双対問題は、(23)式および(24)式に帰着します。
$$
\underset{{\alpha}^i}{max},-\frac{1}{\nu}\sum\sum{\alpha}^i{\alpha}^jK({\bf x}^i,{\bf x}^j)+\sum{\alpha}^i K({\bf x}^i,{\bf x}^i)\hspace{1cm}・・・(23)
$$
$$
s.t.;\sum{\alpha}^i=\nu,;0\leq{\alpha}^i\leq\frac{1}{M}\hspace{1cm}・・・(24)
$$
ここに、$K({\bf x}^i,{\bf x}^j)$ 、$K({\bf x}^i,{\bf x}^i)$ は、(8)式で定義されるカーネル関数です。そして、(23)式および(24)式を解くことで、双対変数 $\alpha^i$ の値が得られます。得られた $\alpha^i$ の値を用いて、円の中心 $\bf c$ は、(25)式で与えられます。
$$
{\bf c}=\frac{1}{\nu}\sum\alpha^i{\bf\phi}({\bf x}^i)\hspace{1cm}・・・(25)
$$
従って、円の中心 $\bf c$と $\phi({\bf x})$ との距離 $l$ の二乗値は、(26)式で与えられます。
$$
\begin{eqnarray}
l^2&=&||,{\bf\phi}({\bf x}),–,{\bf c},||^2\
\
&=&{\bf\phi}({\bf x})^T{\bf\phi}({\bf x})-2{\bf\phi}({\bf x})^T{\bf c}+{\bf c}^T{\bf c}\
\
&=&{\bf\phi}({\bf x})^T{\bf\phi}({\bf x})-\frac{2}{\nu}\sum\alpha^i{\bf\phi}({\bf x})^T{\bf\phi}({\bf x}^i)+\frac{1}{{\nu}^2}\sum\sum\alpha^i\alpha^j{\bf\phi}({\bf x}^i)^T{\bf\phi}({\bf x}^j)\
\
&=&K({\bf x},{\bf x})-\frac{2}{\nu}\sum\alpha^iK({\bf x},{\bf x}^i)+\frac{1}{{\nu}^2}\sum\sum\alpha^i\alpha^jK({\bf x}^i,{\bf x}^j)\hspace{1cm}・・・(26)
\end{eqnarray}
$$
このとき、円の半径の二乗値 $R^2$ は、(26)式の ${\bf x}$ に、下記の条件を満たす ${{\bf x}'}^i$ を代入して得ます。
$$
{{\bf x}’}^i : 0 < \alpha^i < \frac{1}{M},のときの,{\bf x}
$$
上記の条件は、 ${{\bf x}'}^i$ が円周上にあることを意味し、いわゆるサポートベクトルであることを意味します。テスト時は、テストデータ ${\bf x}$ と円の中心の距離 $l$ の二乗値を(26)式から求めます。$l^2\leq R^2$ のとき、テストデータ ${\bf x}$ は、正常範囲である円の内側もしくは円周上にありますので、正常と判定します。$l^2>R^2$ のとき、テストデータ ${\bf x}$ は、正常範囲である円の外側にありますので、異常と判定します。このように、サポートベクトル領域記述法では、(26)式を用いて円の半径 $R$ の二乗値を求め、また、テストデータが正常であるか異常であるかを判定するときも(26)式を用います。
最適化の式である(23)式およびテスト時に用いる(26)式を見ますと、非線形関数 ${\bf \phi}({\bf x})$ を直接扱わなくなくて済んでます。「サポートベクトル領域記述法の式においては、非線形関数は内積の形でしか現れない」ということに着目し、「非線形関数の内積はカーネル関数という扱いやすい関数に置き換えられる」ということをうまく利用したことで、比較的簡便に非線形関数のパラメータを最適化でき、また、テストデータの正常/異常判定ができるようになっています。このような性質をカーネルトリックと呼び、同じく非線形関数を用いる2クラス非線形SVMでもカーネルトリックが現れています。
以上、前章で示しました図4の右側にあたります円の内側と外側で○と×を分類する1クラス非線形SVMであるサポートベクトル領域記述法について説明しました。なお、SVMのパラメータ最適化をラグランジュの双対問題として解く手順については、2クラスソフトマージン線形SVMの記事で紹介しておりますので、ご参考頂ければと思います。
5. おわりに
今回は、1クラス非線形SVMの1形態でありますサポートベクトル領域記述法と呼ばれるSVMについておさらいしました。サポートベクトル領域記述法の定式化をできるだけわかりやすいアプローチで紹介したつもりです。サポートベクトル領域記述法も2クラス非線形SVMと同じく、カーネルトリックを用いることで数学的に扱いやすくなっていること、また、2クラス線形SVMおよび2クラス非線形SVMと同じく、ラグランジュの双対問題を経て、1つの双対変数を最適化する問題に帰着する点が面白いと思って頂けた方もいらっしゃるのではないでしょうか。1クラス非線形SVMは、今回ご紹介しましたサポートベクトル領域記述法の他に1クラス$\nu$サポートベクトルマシンがあります。また、2クラスSVMとして、2クラス線形SVM、2クラス非線形SVMがあります。これらについては他の記事で紹介しますので、ご興味のある方はご参考下さい。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
竹内 一郎、鳥山昌幸:サポートベクトルマシン
赤穂昭太郎:カーネル多変量解析